- Research Article
- Open access
- Published:
Fixed Points and Hyers-Ulam-Rassias Stability of Cauchy-Jensen Functional Equations in Banach Algebras
Fixed Point Theory and Applications volume 2007, Article number: 050175 (2007)
Abstract
We prove the Hyers-Ulam-Rassias stability of homomorphisms in real Banach algebras and of generalized derivations on real Banach algebras for the following Cauchy-Jensen functional equations:  ,
,  , which were introduced and investigated by Baak (2006). The concept of Hyers-Ulam-Rassias stability originated from Th. M. Rassias' stability theorem that appeared in his paper (1978).
, which were introduced and investigated by Baak (2006). The concept of Hyers-Ulam-Rassias stability originated from Th. M. Rassias' stability theorem that appeared in his paper (1978).
References
Ulam SM: A Collection of Mathematical Problems, Interscience Tracts in Pure and Applied Mathematics, no. 8. Interscience, New York, NY, USA; 1960:xiii+150.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941,27(4):222–224. 10.1073/pnas.27.4.222
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978,72(2):297–300. 10.1090/S0002-9939-1978-0507327-1
Găvruţa P: A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. Journal of Mathematical Analysis and Applications 1994,184(3):431–436. 10.1006/jmaa.1994.1211
Park C-G: On the stability of the linear mapping in Banach modules. Journal of Mathematical Analysis and Applications 2002,275(2):711–720. 10.1016/S0022-247X(02)00386-4
Park C-G: Modified Trif's functional equations in Banach modules over a
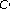 -algebra and approximate algebra homomorphisms. Journal of Mathematical Analysis and Applications 2003,278(1):93–108. 10.1016/S0022-247X(02)00573-5
-algebra and approximate algebra homomorphisms. Journal of Mathematical Analysis and Applications 2003,278(1):93–108. 10.1016/S0022-247X(02)00573-5Park C-G: On an approximate automorphism on a
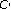 -algebra. Proceedings of the American Mathematical Society 2004,132(6):1739–1745. 10.1090/S0002-9939-03-07252-6
-algebra. Proceedings of the American Mathematical Society 2004,132(6):1739–1745. 10.1090/S0002-9939-03-07252-6Park C-G: Lie
 -homomorphisms between Lie
-homomorphisms between Lie 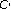 -algebras and Lie
-algebras and Lie  -derivations on Lie
-derivations on Lie 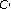 -algebras. Journal of Mathematical Analysis and Applications 2004,293(2):419–434. 10.1016/j.jmaa.2003.10.051
-algebras. Journal of Mathematical Analysis and Applications 2004,293(2):419–434. 10.1016/j.jmaa.2003.10.051Park C-G: Homomorphisms between Lie
 -algebras and Cauchy-Rassias stability of Lie
-algebras and Cauchy-Rassias stability of Lie 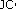 -algebra derivations. Journal of Lie Theory 2005,15(2):393–414.
-algebra derivations. Journal of Lie Theory 2005,15(2):393–414.Park C-G: Homomorphisms between Poisson
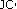 -algebras. Bulletin of the Brazilian Mathematical Society 2005,36(1):79–97. 10.1007/s00574-005-0029-z
-algebras. Bulletin of the Brazilian Mathematical Society 2005,36(1):79–97. 10.1007/s00574-005-0029-zPark C-G: Hyers-Ulam-Rassias stability of a generalized Euler-Lagrange type additive mapping and isomorphisms between
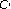 -algebras. Bulletin of the Belgian Mathematical Society. Simon Stevin 2006,13(4):619–632.
-algebras. Bulletin of the Belgian Mathematical Society. Simon Stevin 2006,13(4):619–632.Park C: Hyers-Ulam-Rassias stability of a generalized Apollonius-Jensen type additive mapping and isomorphisms between -algebras. to appear in Mathematische Nachrichten
Park C, Hou J: Homomorphisms between
 -algebras associated with the Trif functional equation and linear derivations on
-algebras associated with the Trif functional equation and linear derivations on  -algebras. Journal of the Korean Mathematical Society 2004,41(3):461–477.
-algebras. Journal of the Korean Mathematical Society 2004,41(3):461–477.Rassias ThM: Problem 16; 2; Report of the 27th International Symposium on Functional Equations. Aequationes Mathematicae 1990,39(2–3):292–293, 309.
Rassias ThM: The problem of S. M. Ulam for approximately multiplicative mappings. Journal of Mathematical Analysis and Applications 2000,246(2):352–378. 10.1006/jmaa.2000.6788
Rassias ThM: On the stability of functional equations in Banach spaces. Journal of Mathematical Analysis and Applications 2000,251(1):264–284. 10.1006/jmaa.2000.7046
Rassias JM: On approximation of approximately linear mappings by linear mappings. Bulletin des Sciences Mathématiques 1984,108(4):445–446.
Rassias JM: Solution of a problem of Ulam. Journal of Approximation Theory 1989,57(3):268–273. 10.1016/0021-9045(89)90041-5
Rassias JM: On approximation of approximately linear mappings by linear mappings. Journal of Functional Analysis 1982,46(1):126–130. 10.1016/0022-1236(82)90048-9
Cădariu L, Radu V: Fixed points and the stability of Jensen's functional equation. Journal of Inequalities in Pure and Applied Mathematics 2003,4(1, article 4):7.
Diaz JB, Margolis B: A fixed point theorem of the alternative, for contractions on a generalized complete metric space. Bulletin of the American Mathematical Society 1968, 74: 305–309. 10.1090/S0002-9904-1968-11933-0
Baak C: Cauchy-Rassias stability of Cauchy-Jensen additive mappings in Banach spaces. Acta Mathematica Sinica 2006,22(6):1789–1796. 10.1007/s10114-005-0697-z
Ara P, Mathieu M: Local Multipliers of C∗-Algebras, Springer Monographs in Mathematics. Springer, London, UK; 2003:xii+319.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Park, C. Fixed Points and Hyers-Ulam-Rassias Stability of Cauchy-Jensen Functional Equations in Banach Algebras. Fixed Point Theory Appl 2007, 050175 (2007). https://doi.org/10.1155/2007/50175
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/50175
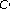 -algebra and approximate algebra homomorphisms. Journal of Mathematical Analysis and Applications 2003,278(1):93–108. 10.1016/S0022-247X(02)00573-5
-algebra and approximate algebra homomorphisms. Journal of Mathematical Analysis and Applications 2003,278(1):93–108. 10.1016/S0022-247X(02)00573-5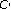 -algebra. Proceedings of the American Mathematical Society 2004,132(6):1739–1745. 10.1090/S0002-9939-03-07252-6
-algebra. Proceedings of the American Mathematical Society 2004,132(6):1739–1745. 10.1090/S0002-9939-03-07252-6 -homomorphisms between Lie
-homomorphisms between Lie 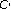 -algebras and Lie
-algebras and Lie  -derivations on Lie
-derivations on Lie 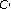 -algebras. Journal of Mathematical Analysis and Applications 2004,293(2):419–434. 10.1016/j.jmaa.2003.10.051
-algebras. Journal of Mathematical Analysis and Applications 2004,293(2):419–434. 10.1016/j.jmaa.2003.10.051 -algebras and Cauchy-Rassias stability of Lie
-algebras and Cauchy-Rassias stability of Lie 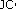 -algebra derivations. Journal of Lie Theory 2005,15(2):393–414.
-algebra derivations. Journal of Lie Theory 2005,15(2):393–414. -algebras. Bulletin of the Brazilian Mathematical Society 2005,36(1):79–97. 10.1007/s00574-005-0029-z
-algebras. Bulletin of the Brazilian Mathematical Society 2005,36(1):79–97. 10.1007/s00574-005-0029-z -algebras. Bulletin of the Belgian Mathematical Society. Simon Stevin 2006,13(4):619–632.
-algebras. Bulletin of the Belgian Mathematical Society. Simon Stevin 2006,13(4):619–632. -algebras associated with the Trif functional equation and linear derivations on
-algebras associated with the Trif functional equation and linear derivations on  -algebras. Journal of the Korean Mathematical Society 2004,41(3):461–477.
-algebras. Journal of the Korean Mathematical Society 2004,41(3):461–477.