- Research Article
- Open access
- Published:
A New Hybrid Iterative Algorithm for Fixed-Point Problems, Variational Inequality Problems, and Mixed Equilibrium Problems
Fixed Point Theory and Applications volume 2008, Article number: 417089 (2008)
Abstract
We introduce a new hybrid iterative algorithm for finding a common element of the set of fixed points of an infinite family of nonexpansive mappings, the set of solutions of the variational inequality of a monotone mapping, and the set of solutions of a mixed equilibrium problem. This study, proves a strong convergence theorem by the proposed hybrid iterative algorithm which solves fixed-point problems, variational inequality problems, and mixed equilibrium problems.
1. Introduction
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Recall that a mapping
. Recall that a mapping  is called contractive if there exists a constant
is called contractive if there exists a constant  such that
such that  for all
for all  . A mapping
. A mapping  is said to be nonexpansive if
is said to be nonexpansive if  for all
for all  . Denote the set of fixed points of
. Denote the set of fixed points of  by
by  .
.
Let  be a real-valued function and
be a real-valued function and  be an equilibrium bifunction, that is,
be an equilibrium bifunction, that is,  for each
for each  . The mixed equilibrium problem (for short, MEP) is to find
. The mixed equilibrium problem (for short, MEP) is to find  such that
such that

In particular, if  , this problem reduces to the equilibrium problem (for short, EP), which is to find
, this problem reduces to the equilibrium problem (for short, EP), which is to find  such that
such that

Denote the set of solutions of MEP by  . The mixed equilibrium problems include fixed-point problems, optimization problems, variational inequality problems, Nash equilibrium problems, and the equilibrium problems as special cases (see, e.g., [1–5]). Some methods have been proposed to solve the MEP and EP (see, e.g., [5–14]). In 1997, Combettes and Hirstoaga [13] introduced an iterative method of finding the best approximation to the initial data and proved a strong convergence theorem. Subsequently, S. Takahashi and W. Takahashi [8] introduced another iterative scheme for finding a common element of the set of solutions of EP and the set of fixed-point points of a nonexpansive mapping. Yao et al. [12] considered an iterative scheme for finding a common element of the set of solutions of EP and the set of common fixed points of an infinite nonexpansive mappings. Very recently, Zeng and Yao [14] considered a new iterative scheme for finding a common element of the set of solutions of MEP and the set of common fixed points of finitely many nonexpansive mappings. Their results extend and improve many results in the literature.
. The mixed equilibrium problems include fixed-point problems, optimization problems, variational inequality problems, Nash equilibrium problems, and the equilibrium problems as special cases (see, e.g., [1–5]). Some methods have been proposed to solve the MEP and EP (see, e.g., [5–14]). In 1997, Combettes and Hirstoaga [13] introduced an iterative method of finding the best approximation to the initial data and proved a strong convergence theorem. Subsequently, S. Takahashi and W. Takahashi [8] introduced another iterative scheme for finding a common element of the set of solutions of EP and the set of fixed-point points of a nonexpansive mapping. Yao et al. [12] considered an iterative scheme for finding a common element of the set of solutions of EP and the set of common fixed points of an infinite nonexpansive mappings. Very recently, Zeng and Yao [14] considered a new iterative scheme for finding a common element of the set of solutions of MEP and the set of common fixed points of finitely many nonexpansive mappings. Their results extend and improve many results in the literature.
Let  of
of  into
into  be a nonlinear mapping. It is well known that the variational inequality problem is to find
be a nonlinear mapping. It is well known that the variational inequality problem is to find  such that
such that

The set of solutions of the variational inequality problem is denoted by  . A mapping
. A mapping  is called
is called  -inverse-strongly monotone if there exists a positive real number
-inverse-strongly monotone if there exists a positive real number  such that
such that

Recently, some authors have proposed new iterative algorithms to approximate a common element of the set of fixed points of a nonxpansive mapping and the set of solutions of the variational inequality. For the details, see [15, 16] and the references therein.
Motivated by the recent works, in this paper we introduce a new hybrid iterative algorithm for finding a common element of the set of fixed points of an infinite family of nonexpansive mappings, the set of solutions of the variational inequality of a monotone mapping, and the set of solutions of a mixed equilibrium problem. We prove a strong convergence theorem by the proposed hybrid iterative algorithm which solves fixed-point problems, variational inequality problems, and mixed equilibrium problems.
2. Preliminaries
Let  be a real Hilbert space with inner product
be a real Hilbert space with inner product  and norm
and norm  . Let
. Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Then for any
. Then for any  , there exists a unique nearest point in
, there exists a unique nearest point in  , denoted by
, denoted by  such that
such that

Such a  is called the metric projection of
is called the metric projection of  onto
onto  . It is well known that
. It is well known that  is a nonexpansive mapping and satisfies
is a nonexpansive mapping and satisfies

Moreover,  is characterized by the following properties:
is characterized by the following properties:

It is clear that

In this paper, for solving the mixed equilibrium problems for an equilibrium bifunction  , we assume that
, we assume that  satisfies the following conditions:
satisfies the following conditions:
(H1)  is monotone, that is,
is monotone, that is,  for all
for all  ;
;
(H2) for each fixed  ,
,  is concave and upper semicontinuous;
is concave and upper semicontinuous;
(H3) for each  ,
,  is convex.
is convex.
A mapping  is called Lipschitz continuous if there exists a constant
is called Lipschitz continuous if there exists a constant  such that
such that

A differentiable function  on a convex set
on a convex set  is called:
is called:
-
(i)
 -convex if
-convex if  (2.6)
(2.6)
where  is the Fréchet derivative of
is the Fréchet derivative of  at
at  ;
;
-
(ii)
 -strongly convex if there exists a constant
-strongly convex if there exists a constant  such that
such that 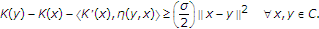 (2.7)
(2.7)
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  ,
,  be a real-valued function, and
be a real-valued function, and  be an equilibrium bifunction. Let
be an equilibrium bifunction. Let  be a positive number. For a given point
be a positive number. For a given point  , the auxiliary problem for MEP consists of finding
, the auxiliary problem for MEP consists of finding  such that
such that

Let  be the mapping such that for each
be the mapping such that for each  ,
,  is the solution set of the auxiliary problem MEP, that is,
is the solution set of the auxiliary problem MEP, that is,

We first need the following important and interesting result.
Lemma 2.1 (see [14]).
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  and let
and let  be a lower semicontinuous and convex functional. Let
be a lower semicontinuous and convex functional. Let  be an equilibrium bifunction satisfying conditions (H1)–(H3). Assume that
be an equilibrium bifunction satisfying conditions (H1)–(H3). Assume that
-
(i)
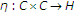 is Lipschitz continuous with constant
is Lipschitz continuous with constant
 such that
such that
-
(a)
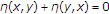 for all
for all ,
, -
(b)
 is affine in the first variable,
is affine in the first variable, -
(c)
for each fixed
 ,
,  is sequentially continuous from the weak topology to the weak topology;
is sequentially continuous from the weak topology to the weak topology;
-
(ii)
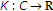 is
is  -strongly convex with constant
-strongly convex with constant and its derivative
and its derivative is sequentially continuous from the weak topology to the strong topology;
is sequentially continuous from the weak topology to the strong topology; -
(iii)
for each
 , there exist a bounded subset
, there exist a bounded subset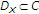 and
and such that for any
such that for any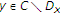 ,
, 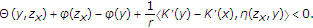 (2.10)
(2.10)
Then there hold the following:
-
(i)
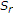 is single-valued;
is single-valued; -
(ii)
 is nonexpansive if
is nonexpansive if
 is Lipschitz continuous with constant
is Lipschitz continuous with constant
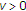 such that
such that
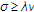 and
and
 (2.11)
(2.11)
where  for
for  ;
;
-
(iii)
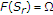 ;
; -
(vi)
 is closed and convex.
is closed and convex.
We also need the following lemmas for proving our main results.
Lemma 2.2 (see [17]).
Let  and
and  be bounded sequences in a Banach space
be bounded sequences in a Banach space  and let
and let  be a sequence in
be a sequence in  with
with  . Suppose
. Suppose  for all integers
for all integers  and
and  . Then
. Then  .
.
Lemma 2.3 (see [18]).
Assume  is a sequence of nonnegative real numbers such that
is a sequence of nonnegative real numbers such that  , where
, where  is a sequence in
is a sequence in  and
and  is a sequence such that
is a sequence such that
-
(1)
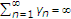 ;
; -
(2)
 or
or  .
.
Then  .
.
3. Iterative Algorithm and Strong Convergence Theorems
In this section, we first introduce a new iterative algorithm. Consequently, we will establish a strong convergence theorem for this iteration algorithm. To be more specific, let  be infinite mappings of
be infinite mappings of  into itself and let
into itself and let  be real numbers such that
be real numbers such that  for every
for every  . For any
. For any  , define a mapping
, define a mapping  of
of  into itself as follows:
into itself as follows:

Such  is called the
is called the  -mapping generated by
-mapping generated by  and
and  . For the iterative algorithm for a finite family of nonexpansive mappings, we refer the reader to [19].
. For the iterative algorithm for a finite family of nonexpansive mappings, we refer the reader to [19].
We have the following crucial Lemmas 3.1 and 3.2 concerning  which can be found in [20]. Now we only need the following similar version in Hilbert spaces.
which can be found in [20]. Now we only need the following similar version in Hilbert spaces.
Lemma 3.1.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be nonexpansive mappings of
be nonexpansive mappings of  into itself such that
into itself such that  is nonempty, and let
is nonempty, and let  be real numbers such that
be real numbers such that  for any
for any  . Then for every
. Then for every  and
and  , the limit
, the limit  exists.
exists.
Lemma 3.2.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be nonexpansive mappings of
be nonexpansive mappings of  into itself such that
into itself such that  is nonempty, and let
is nonempty, and let  be real numbers such that
be real numbers such that  for any
for any  . Then
. Then  .
.
The following remark [12] is important to prove our main results.
Remark 3.3.
Using Lemma 3.1, one can define a mapping  of
of  into itself as
into itself as  for every
for every  . If
. If  is a bounded sequence in
is a bounded sequence in  , then we have
, then we have

Throughout this paper, we will assume that  for every
for every  .
.
Now we introduce the following iteration algorithm.
Algorithm 3.4.
Let  be a constant. Let
be a constant. Let  be a lower semicontinuous and convex functional and let
be a lower semicontinuous and convex functional and let  be an equilibrium bifunction. Let
be an equilibrium bifunction. Let  be a
be a  -inverse-strongly monotone mapping and
-inverse-strongly monotone mapping and  be the
be the  -mapping defined by (3.1). Let
-mapping defined by (3.1). Let  be a contraction of
be a contraction of  into itself with coefficient
into itself with coefficient  and given
and given  arbitrarily. Suppose that the sequences
arbitrarily. Suppose that the sequences  and
and  are generated iteratively by
are generated iteratively by

where  ,
,  , and
, and  are three sequences in
are three sequences in  , and
, and  is a sequence in
is a sequence in  .
.
Now we study the strong convergence of the hybrid iterative algorithm (3.3).
Theorem 3.5.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  and let
and let  be a lower semicontinuous and convex functional. Let
be a lower semicontinuous and convex functional. Let  be an equilibrium bifunction satisfying conditions (H1)–(H3) and let
be an equilibrium bifunction satisfying conditions (H1)–(H3) and let  be an infinite family of nonexpansive mappings of
be an infinite family of nonexpansive mappings of  into itself. Let
into itself. Let  be a
be a  -inverse-strongly monotone mapping such that
-inverse-strongly monotone mapping such that  . Suppose
. Suppose  ,
,  , and
, and  are three sequences in
are three sequences in  with
with  . Assume that
. Assume that
-
(i)
 is Lipschitz continuous with constant
is Lipschitz continuous with constant
 such that
such that
-
(a)
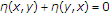 for all
for all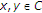 ,
, -
(b)
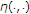 is affine in the first variable,
is affine in the first variable, -
(c)
for each fixed
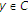 ,
,  is sequentially continuous from the weak topology to the weak topology;
is sequentially continuous from the weak topology to the weak topology;
-
(ii)
 is
is - strongly convex with constant
- strongly convex with constant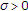 and its derivative
and its derivative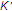 is not only sequentially continuous from the weak topology to the strong topology but also Lipschitz continuous with constant
is not only sequentially continuous from the weak topology to the strong topology but also Lipschitz continuous with constant such that
such that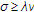 ;
; -
(iii)
for each
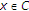 ; there exist a bounded subset
; there exist a bounded subset and
and such that for any
such that for any ,
,  (3.4)
(3.4)
-
(iv)
 ,
,  ,
, 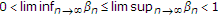 ,
,  , and
, and  .
.
Let  be a contraction of
be a contraction of  into itself and given
into itself and given  arbitrarily. Then the sequence
arbitrarily. Then the sequence  generated by (3.3) converges strongly to
generated by (3.3) converges strongly to  , where
, where  provided that
provided that  is firmly nonexpansive.
is firmly nonexpansive.
Proof.
We first note that  is a contraction with coefficient
is a contraction with coefficient  . Then
. Then 

 for all
for all  . Therefore
. Therefore  is a contraction of
is a contraction of  into itself which implies that there exists a unique element
into itself which implies that there exists a unique element  such that
such that  .
.
Next we divide the following proofs into several steps.
Step 1 (  ,
,  , and
, and  are bounded).
are bounded).
Let  . From the definition of
. From the definition of  , we know that
, we know that  . It follows that
. It follows that

For all  and
and  , we note that
, we note that

which implies that  is nonexpansive.
is nonexpansive.
Set  for all
for all  . From (2.4), we have that
. From (2.4), we have that  . It follows from (3.6) that
. It follows from (3.6) that

Hence we obtain that

Therefore  is bounded, so are
is bounded, so are  and
and  .
.
Step 2 ( ).
).
Setting  for all
for all  . It follows that
. It follows that

which implies that

Now we estimate  and
and  .
.
From (3.1), since  and
and  are nonexpansive, we have
are nonexpansive, we have

where  is a constant such that
is a constant such that  .
.
At the same time, we observe that

Since  and
and  , from the nonexpansivity of
, from the nonexpansivity of  , we get
, we get

Substituting (3.11)–(3.13) into (3.10), we have

Since  , and
, and  , we have
, we have

Hence by Lemma 2.2, we have

Consequently,

Step 3 ( ).
).
Note that  . Then we have
. Then we have

For  , noting that
, noting that  is firmly nonexpansive, we have
is firmly nonexpansive, we have

and hence

So, we have

that is,

From (3.6), we obtain that

Then we have

which implies that

We note that

Then we derive

Hence

which implies that

Since  , we have
, we have

Combining the above inequality, (3.18)–(3.29), and Remark 3.3, we have

Step 4 ( , where
, where  ).
).
To show the above inequality, we can choose a subsequence  of
of  such that
such that

Since  is bounded, there exists a subsequence
is bounded, there exists a subsequence  of
of  which converges weakly to
which converges weakly to  . Without loss of generality, we can assume that
. Without loss of generality, we can assume that  . From
. From  , we obtain
, we obtain  .
.
First, we show  . Assume that
. Assume that  . Since
. Since  and
and  , by Opial's condition, we have
, by Opial's condition, we have

which is a contradiction. Hence we get  . By the same argument as that in the proof of [21, Theorem 3.1], we can prove that
. By the same argument as that in the proof of [21, Theorem 3.1], we can prove that  ; and by the same argument as that in the proof of [14, Theorem 4.1], we also can prove that
; and by the same argument as that in the proof of [14, Theorem 4.1], we also can prove that  . Hence
. Hence  .
.
Since  and
and  , we have
, we have

Step 5 ( , where
, where  ).
).
From (3.3), we have

that is,

It is easy to see that  and
and

Applying Lemma 2.3 and (3.34) to (3.36), we conclude that  as
as  . This completes the proof.
. This completes the proof.
Concerning  , we give the following remark.
, we give the following remark.
Remark 3.6.
For each  , we denote
, we denote  and
and  . Then for all
. Then for all  , we have
, we have


Taking  in (3.38) and
in (3.38) and  in (3.39), and adding up these two inequalities, we obtain
in (3.39), and adding up these two inequalities, we obtain

Note that  and
and  . Hence from (3.40), we deduce
. Hence from (3.40), we deduce

which implies that

Since  is
is  -strongly monotone with constant
-strongly monotone with constant  , then from (3.42), we conclude that
, then from (3.42), we conclude that

Take  ,
,  , and
, and  . Then from (3.43), we have
. Then from (3.43), we have

This indicates that  is firmly nonexpansive.
is firmly nonexpansive.
Corollary 3.7.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  and let
and let  be a lower semicontinuous and convex functional. Let
be a lower semicontinuous and convex functional. Let  be an equilibrium bifunction satisfying conditions (H1)–(H3). Let
be an equilibrium bifunction satisfying conditions (H1)–(H3). Let  be a
be a  -inverse-strongly monotone mapping such that
-inverse-strongly monotone mapping such that  . Suppose
. Suppose  ,
,  , and
, and  are three sequences in
are three sequences in  with
with  . Assume that
. Assume that
-
(i)
 is Lipschitz continuous with constant
is Lipschitz continuous with constant
 such that
such that
-
(a)
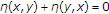 for all
for all ,
, -
(b)
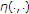 is affine in the first variable,
is affine in the first variable, -
(c)
for each fixed
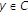 ,
, 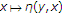 is sequentially continuous from the weak topology to the weak topology;
is sequentially continuous from the weak topology to the weak topology;
-
(ii)
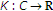 is
is -strongly convex with constant
-strongly convex with constant and its derivative
and its derivative is not only sequentially continuous from the weak topology to the strong topology but also Lipschitz continuous with constant
is not only sequentially continuous from the weak topology to the strong topology but also Lipschitz continuous with constant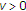 such that
such that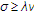 ;
; -
(iii)
for each
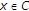 , there exist a bounded subset
, there exist a bounded subset and
and such that, for any
such that, for any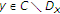 ,
, 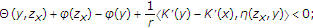 (3.45)
(3.45)
-
(iv)
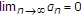 ,
, 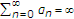 ,
, 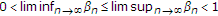 ,
, 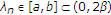 , and
, and 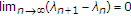 .
.
Let  be a contraction of
be a contraction of  into itself and given
into itself and given  arbitrarily. Let the sequences
arbitrarily. Let the sequences  ,
,  , and
, and  be generated iteratively by
be generated iteratively by

Then the sequence  generated by (3.46) converges strongly to
generated by (3.46) converges strongly to  , where
, where  provided that
provided that  is firmly nonexpansive.
is firmly nonexpansive.
Proof.
Take  for all
for all  , and for all
, and for all  in (3.1). Then
in (3.1). Then  for all
for all  . The conclusion follows immediately from Theorem 3.5. This completes the proof.
. The conclusion follows immediately from Theorem 3.5. This completes the proof.
Corollary 3.8.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be an infinite family of nonexpansive mappings of
be an infinite family of nonexpansive mappings of  into itself. Let
into itself. Let  be a
be a  -inverse-strongly monotone mapping such that
-inverse-strongly monotone mapping such that  . Suppose
. Suppose  ,
,  , and
, and  are three sequences in
are three sequences in  with
with  ,
,  . Assume that
. Assume that
-
(i)
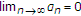 and
and 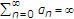 ;
; -
(ii)
 ;
; -
(iii)
 and
and

Let  be a contraction of
be a contraction of  into itself and given
into itself and given  arbitrarily. Then the sequence
arbitrarily. Then the sequence  , generated iteratively by
, generated iteratively by

converges strongly to  , where
, where  .
.
Proof.
Set  and
and  for all
for all  and put
and put  . Take
. Take  and
and  for all
for all  . Then we have
. Then we have  . Hence the conclusion follows. This completes the proof.
. Hence the conclusion follows. This completes the proof.
References
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994, 63(1–4):123-145.
Zeng L-C, Wu S-Y, Yao J-C: Generalized KKM theorem with applications to generalized minimax inequalities and generalized equilibrium problems. Taiwanese Journal of Mathematics 2006, 10(6):1497-1514.
Chadli O, Wong NC, Yao J-C: Equilibrium problems with applications to eigenvalue problems. Journal of Optimization Theory and Applications 2003, 117(2):245-266. 10.1023/A:1023627606067
Chadli O, Schaible S, Yao J-C: Regularized equilibrium problems with application to noncoercive hemivariational inequalities. Journal of Optimization Theory and Applications 2004, 121(3):571-596.
Konnov IV, Schaible S, Yao J-C: Combined relaxation method for mixed equilibrium problems. Journal of Optimization Theory and Applications 2005, 126(2):309-322. 10.1007/s10957-005-4716-0
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. Journal of Nonlinear and Convex Analysis 2005, 6(1):117-136.
Flåm SD, Antipin AS: Equilibrium programming using proximal-like algorithms. Mathematical Programming 1996, 78(1):29-41. 10.1007/BF02614504
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007, 331(1):506-515. 10.1016/j.jmaa.2006.08.036
Chadli O, Konnov IV, Yao J-C: Descent methods for equilibrium problems in a Banach space. Computers & Mathematics with Applications 2004, 48(3-4):609-616. 10.1016/j.camwa.2003.05.011
Ding XP, Lin YC, Yao J-C: Predictor-corrector algorithms for solving generalized mixed implicit quasi-equilibrium problems. Applied Mathematics and Mechanics 2006, 27(9):1157-1164. 10.1007/s10483-006-0901-1
Tada A, Takahashi W: Strong convergence theorem for an equilibrium problem and a nonexpansive mapping. In Nonlinear Analysis and Convex Analysis. Edited by: Takahashi W, Tanaka T. Yokohama Publishers, Yokohama, Japan; 2007:609-617.
Yao Y, Liou Y-C, Yao J-C: Convergence theorem for equilibrium problems and fixed point problems of infinite family of nonexpansive mappings. Fixed Point Theory and Applications 2007, 2007:-12.
Combettes PL, Hirstoaga AS: Equilibrium programming using proximal-like algorithms. Mathematical Programming 1997, 78(1):29-41.
Zeng L-C, Yao J-C: A hybrid iterative scheme for mixed equilibrium problems and fixed point problems. Journal of Computational and Applied Mathematics 2008, 214(1):186-201. 10.1016/j.cam.2007.02.022
Zeng L-C, Yao J-C: Strong convergence theorem by an extragradient method for fixed point problems and variational inequality problems. Taiwanese Journal of Mathematics 2006, 10(5):1293-1303.
Yao Y, Yao J-C: On modified iterative method for nonexpansive mappings and monotone mappings. Applied Mathematics and Computation 2007, 186(2):1551-1558. 10.1016/j.amc.2006.08.062
Suzuki T: Strong convergence theorems for infinite families of nonexpansive mappings in general Banach spaces. Fixed Point Theory and Applications 2005, 2005(1):103-123. 10.1155/FPTA.2005.103
Xu H-K: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004, 298(1):279-291. 10.1016/j.jmaa.2004.04.059
Kuhfittig PKF: Common fixed points of nonexpansive mappings by iteration. Pacific Journal of Mathematics 1981, 97(1):137-139.
Shimoji K, Takahashi W: Strong convergence to common fixed points of infinite nonexpansive mappings and applications. Taiwanese Journal of Mathematics 2001, 5(2):387-404.
Nadezhkina N, Takahashi W: Weak convergence theorem by an extragradient method for nonexpansive mappings and monotone mappings. Journal of Optimization Theory and Applications 2006, 128(1):191-201. 10.1007/s10957-005-7564-z
Acknowledgments
The authors are extremely grateful to the anonymous referees and Professor T. Suzuki for their useful comments and suggestions. The first author was partially supposed by National Natural Science Foundation of China Grant no. 10771050. The second author was partially supposed by the Grant no. NSC 96-2221-E-230-003.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yao, Y., Liou, YC. & Yao, JC. A New Hybrid Iterative Algorithm for Fixed-Point Problems, Variational Inequality Problems, and Mixed Equilibrium Problems. Fixed Point Theory Appl 2008, 417089 (2008). https://doi.org/10.1155/2008/417089
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/417089
 -convex if
-convex if 
 -strongly convex if there exists a constant
-strongly convex if there exists a constant  such that
such that 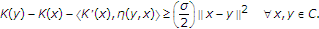
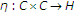 is Lipschitz continuous with constant
is Lipschitz continuous with constant
 such that
such that
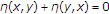 for all
for all ,
, is affine in the first variable,
is affine in the first variable, ,
,  is sequentially continuous from the weak topology to the weak topology;
is sequentially continuous from the weak topology to the weak topology;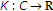 is
is  -strongly convex with constant
-strongly convex with constant and its derivative
and its derivative is sequentially continuous from the weak topology to the strong topology;
is sequentially continuous from the weak topology to the strong topology; , there exist a bounded subset
, there exist a bounded subset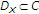 and
and such that for any
such that for any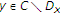 ,
, 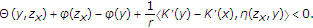
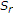 is single-valued;
is single-valued; is nonexpansive if
is nonexpansive if
 is Lipschitz continuous with constant
is Lipschitz continuous with constant
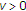 such that
such that
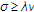 and
and

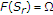 ;
; is closed and convex.
is closed and convex.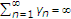 ;
; or
or  .
. is Lipschitz continuous with constant
is Lipschitz continuous with constant
 such that
such that
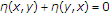 for all
for all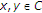 ,
,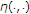 is affine in the first variable,
is affine in the first variable,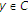 ,
,  is sequentially continuous from the weak topology to the weak topology;
is sequentially continuous from the weak topology to the weak topology; is
is - strongly convex with constant
- strongly convex with constant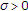 and its derivative
and its derivative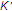 is not only sequentially continuous from the weak topology to the strong topology but also Lipschitz continuous with constant
is not only sequentially continuous from the weak topology to the strong topology but also Lipschitz continuous with constant such that
such that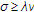 ;
;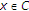 ; there exist a bounded subset
; there exist a bounded subset and
and such that for any
such that for any ,
, 
 ,
,  ,
, 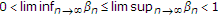 ,
,  , and
, and  .
. is Lipschitz continuous with constant
is Lipschitz continuous with constant
 such that
such that
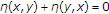 for all
for all ,
,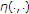 is affine in the first variable,
is affine in the first variable,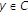 ,
, 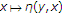 is sequentially continuous from the weak topology to the weak topology;
is sequentially continuous from the weak topology to the weak topology;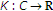 is
is -strongly convex with constant
-strongly convex with constant and its derivative
and its derivative is not only sequentially continuous from the weak topology to the strong topology but also Lipschitz continuous with constant
is not only sequentially continuous from the weak topology to the strong topology but also Lipschitz continuous with constant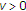 such that
such that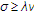 ;
;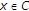 , there exist a bounded subset
, there exist a bounded subset and
and such that, for any
such that, for any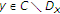 ,
, 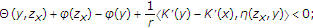
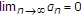 ,
, 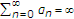 ,
, 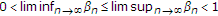 ,
, 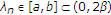 , and
, and 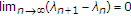 .
.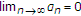 and
and 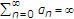 ;
; ;
; and
and
