- Research Article
- Open access
- Published:
Viscosity Approximation Methods for Generalized Mixed Equilibrium Problems and Fixed Points of a Sequence of Nonexpansive Mappings
Fixed Point Theory and Applications volume 2008, Article number: 714939 (2008)
Abstract
We introduce an iterative scheme by the viscosity approximation method for finding a common element of the set of common solutions for generalized mixed equilibrium problems and the set of common fixed points of a sequence of nonexpansive mappings in Hilbert spaces. We show a strong convergence theorem under some suitable conditions.
1. Introduction
Equilibrium problems theory provides us with a unified, natural, innovative, and general framework to study a wide class of problems arising in finance, economics, network analysis, transportation, elasticity, and optimization, which has been extended and generalized in many directions using novel and innovative techniques; see [1–8]. Inspired and motivated by the research and activities going in this fascinating area, we introduce and consider a new class of equilibrium problems, which is known as the generalized mixed equilibrium problems.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  and
and  a multivalued mapping. Let
a multivalued mapping. Let  be a real-valued function and
be a real-valued function and  an equilibrium-like function, that is,
an equilibrium-like function, that is,

We consider the problem of finding  and
and  such that
such that

which is called the generalized mixed equilibrium problem (for short, GMEP). If  is a single-valued mapping, then problem (1.2) is equivalent to finding
is a single-valued mapping, then problem (1.2) is equivalent to finding  such that
such that

We denote  for the set of solutions of GMEP (1.2). This class is a quite general and unifying one and includes several classes of equilibrium problems and variational inequalities as special cases. In recent years, several numerical techniques including projection, resolvent, and auxiliary principle have been developed and analyzed for solving variational inequalities. It is well known that projection- and resolvent-type methods cannot be extended for equilibrium problems. To overcome this drawback, one usually uses the auxiliary principle technique. Glowinski et al. [9] have used this technique to study the existence of a solution of mixed variational inequalities. The viscosity approximation method is one of the important methods for approximation fixed points of nonexpansive type mappings. It was first discussed by Moudafi [10]. Recently, Hirstoaga [11] and S. Takahashi and W. Takahashi [12] applied viscosity approximation technique for finding a common element of set of solutions of an equilibrium problem (EP) and set of fixed points of a nonexpansive mapping. Very recently, Yao et al. [13] introduced and studied an iteration process for finding a common element of the set of solutions of the EP and the set of common fixed points of infinitely many nonexpansive mappings in
for the set of solutions of GMEP (1.2). This class is a quite general and unifying one and includes several classes of equilibrium problems and variational inequalities as special cases. In recent years, several numerical techniques including projection, resolvent, and auxiliary principle have been developed and analyzed for solving variational inequalities. It is well known that projection- and resolvent-type methods cannot be extended for equilibrium problems. To overcome this drawback, one usually uses the auxiliary principle technique. Glowinski et al. [9] have used this technique to study the existence of a solution of mixed variational inequalities. The viscosity approximation method is one of the important methods for approximation fixed points of nonexpansive type mappings. It was first discussed by Moudafi [10]. Recently, Hirstoaga [11] and S. Takahashi and W. Takahashi [12] applied viscosity approximation technique for finding a common element of set of solutions of an equilibrium problem (EP) and set of fixed points of a nonexpansive mapping. Very recently, Yao et al. [13] introduced and studied an iteration process for finding a common element of the set of solutions of the EP and the set of common fixed points of infinitely many nonexpansive mappings in  . Let
. Let  be a sequence of nonexpansive mappings of
be a sequence of nonexpansive mappings of  into itself and let
into itself and let  be a sequence of nonnegative numbers in
be a sequence of nonnegative numbers in  . For any
. For any  , define a mapping
, define a mapping  of
of  into itself as follows:
into itself as follows:

Such a mapping  is called the
is called the  -mapping generated by
-mapping generated by  and
and  , see [14].
, see [14].
The purpose of this paper is to develop an iterative algorithm for finding a common element of set of solutions of GMEP (1.2) and set of common fixed points of a sequence of nonexpansive mappings in Hilbert spaces. The result presented in this paper improves and extends the main result of S. Takahashi and W. Takahashi [12].
2. Preliminaries
Let  be a real Hilbert space with inner product
be a real Hilbert space with inner product  and norm
and norm  , and let
, and let  be a closed convex subset of
be a closed convex subset of  . Then, for any
. Then, for any  , there exists a unique nearest point in
, there exists a unique nearest point in  , denoted by
, denoted by  , such that
, such that

 is called metric projection of
is called metric projection of  onto
onto  . It is well known that
. It is well known that  is nonexpansive. Furthermore, for
is nonexpansive. Furthermore, for  and
and  ,
,

We denote by  the set of fixed points of a self-mapping
the set of fixed points of a self-mapping  on
on  , that is,
, that is,  . It is well known that if
. It is well known that if  is nonempty, bounded, closed, and convex and
is nonempty, bounded, closed, and convex and  is nonexpansive, then
is nonexpansive, then  is nonempty; see [15]. Let
is nonempty; see [15]. Let  be a sequence of nonexpansive mappings of
be a sequence of nonexpansive mappings of  into itself, where
into itself, where  is a nonempty closed convex subset of a real Hilbert space
is a nonempty closed convex subset of a real Hilbert space  . Given a sequence
. Given a sequence  in
in  , we define a sequence
, we define a sequence  of self-mappings on
of self-mappings on  by (1.4). Then we have the following lemmas which are important to prove our results.
by (1.4). Then we have the following lemmas which are important to prove our results.
Lemma 2.1 (see [14]).
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be a sequence of nonexpansive mappings of
be a sequence of nonexpansive mappings of  into itself such that
into itself such that  , and let
, and let  be a sequence in
be a sequence in  for some
for some  . Then, for every
. Then, for every  and
and  the limit
the limit  exists.
exists.
Using Lemma 2.1, one can define mapping  of
of  into itself as follows:
into itself as follows:

for every  . Such a mapping
. Such a mapping  is called the
is called the  -mapping generated by
-mapping generated by  and
and  Throughout this paper, we will assume that
Throughout this paper, we will assume that  for every
for every  . Since
. Since  is nonexpansive,
is nonexpansive,  is also nonexpansive.
is also nonexpansive.
Lemma 2.2 (see [14]).
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  be a sequence of nonexpansive mappings of
be a sequence of nonexpansive mappings of  into itself such that
into itself such that  , and let
, and let  be a sequence in
be a sequence in  for some
for some  . Then,
. Then,  .
.
Let  be a convex subset of a real Hilbert space
be a convex subset of a real Hilbert space  and
and  a Fréchet differential function. Then
a Fréchet differential function. Then  is said to be
is said to be  -convex strongly convex if there exists a constant
-convex strongly convex if there exists a constant  such that
such that

If  , then
, then  is said to be
is said to be  -convex. In particular, if
-convex. In particular, if  for all
for all  , then
, then  is said to be strongly convex.
is said to be strongly convex.
Let  be a nonempty subset of a real Hilbert space
be a nonempty subset of a real Hilbert space  . A bifunction
. A bifunction  is said to be skew-symmetric if
is said to be skew-symmetric if

If the skew-symmetric bifunction  is linear in both arguments, then
is linear in both arguments, then

We denote  for weak convergence and
for weak convergence and  for strong convergence. A function
for strong convergence. A function  is called weakly sequentially continuous at
is called weakly sequentially continuous at  , if
, if  as
as  for each sequence
for each sequence  in
in  converging weakly to
converging weakly to  . The function
. The function  is called weakly sequentially continuous on
is called weakly sequentially continuous on  if it is weakly sequentially continuous at each point of
if it is weakly sequentially continuous at each point of  .
.
Let  denote the set of nonempty closed bounded subsets of
denote the set of nonempty closed bounded subsets of  . For
. For  , define the Hausdorff metric
, define the Hausdorff metric  as follows:
as follows:

Lemma 2.3 (see [16]).
Let  and
and  . Then for
. Then for  , there must exist a point
, there must exist a point  such that
such that  .
.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  and
and  a multivalued mapping. For
a multivalued mapping. For  , let
, let  . Let
. Let  be a real-valued function satisfying the following:
be a real-valued function satisfying the following:

 is skew symmetric;
is skew symmetric;
 for each fixed
for each fixed  ,
,  is convex and upper semicontinuous;
is convex and upper semicontinuous;

 is weakly continuous on
is weakly continuous on  .
.
Let  be a differentiable functional with Fréchet derivative
be a differentiable functional with Fréchet derivative  at
at  satisfying the following:
satisfying the following:

 is sequentially continuous from the weak topology to the strong topology;
is sequentially continuous from the weak topology to the strong topology;

 is Lipschitz continuous with Lipschitz constant
is Lipschitz continuous with Lipschitz constant  .
.
Let  be a function satisfying the following:
be a function satisfying the following:

 for all
for all  ;
;

 is affine in the first coordinate variable;
is affine in the first coordinate variable;
 for each fixed
for each fixed  ,
,  is sequentially continuous from the weak topology to the weak topology.
is sequentially continuous from the weak topology to the weak topology.
Let us consider the equilibrium-like function  which satisfies the following conditions with respect to the multivalued mapping
which satisfies the following conditions with respect to the multivalued mapping  :
:
 for each fixed
for each fixed  ,
,  is an upper semicontinuous function from
is an upper semicontinuous function from  to
to  , that is,
, that is,  and
and  imply
imply  ;
;
 for each fixed
for each fixed  ,
,  is a concave function;
is a concave function;
 for each fixed
for each fixed  ,
,  is a convex function.
is a convex function.
Let  be a positive parameter. For a given element
be a positive parameter. For a given element  and
and  , consider the following auxiliary problem for GMEP(1.2): find
, consider the following auxiliary problem for GMEP(1.2): find  such that
such that

It is easy to see that if  , then
, then  is a solution of GMEP(1.2).
is a solution of GMEP(1.2).
Lemma 2.4 (see [6]).
Let  be a nonempty closed convex bounded subset of a real Hilbert space
be a nonempty closed convex bounded subset of a real Hilbert space  and
and  a real-valued function satisfying the conditions
a real-valued function satisfying the conditions  . Let
. Let  be a multivalued mapping and
be a multivalued mapping and  the equilibrium-like function satisfying the conditions
the equilibrium-like function satisfying the conditions  . Assume that
. Assume that  is a Lipschitz function with Lipschitz constant
is a Lipschitz function with Lipschitz constant  which satisfies the conditions
which satisfies the conditions  . Let
. Let  be an
be an  -strongly convex function with constant
-strongly convex function with constant  which satisfies the conditions
which satisfies the conditions  and
and  . For each
. For each  , let
, let  . For
. For  , define a mapping
, define a mapping  by
by

Then one has the following:
-
(a)
the auxiliary problem (2.8) has a unique solution;
(b) is single valued;
is single valued;
-
(c)
if
 and
and 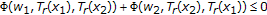 for all
for all 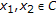 and all
and all 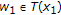 ,
,  , it follows that
, it follows that 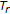 is nonexpansive;
is nonexpansive;
(d) ;
;
(e) is closed and convex.
is closed and convex.
We also need the following lemmas for our main results.
Lemma 2.5 (see [17]).
Let  , and
, and  be three sequences of nonnegative numbers such that
be three sequences of nonnegative numbers such that

If  ,
,  , and
, and  , then
, then  exists.
exists.
Lemma 2.6.
Let  and
and  be sequences of nonnegative numbers such that
be sequences of nonnegative numbers such that

If  and
and  , then
, then  .
.
Proof.
It is easy to see that inequality (2.11) is equivalent to

where  ,
,  and
and  . It follows that
. It follows that

Note that Lemma 2.5 implies that  exists. Suppose
exists. Suppose  for some
for some  . It is obvious that
. It is obvious that  and so inequality (2.12) implies that
and so inequality (2.12) implies that  , which is a contradiction. Thus,
, which is a contradiction. Thus,  . This completes the proof.
. This completes the proof.
Lemma 2.7 (see [6]).
Let  be a sequence in a normed space
be a sequence in a normed space  such that
such that

where  , and
, and  and
and  are sequences satisfy the following conditions:
are sequences satisfy the following conditions:
-
(i)
 for all
for all 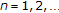 and
and 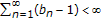 ;
; -
(ii)
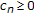 for all
for all 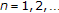 and
and 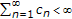 .
.
Then  is a Cauchy sequence.
is a Cauchy sequence.
Lemma 2.8 (see [18]).
Let  be a sequence of nonnegative real numbers such that
be a sequence of nonnegative real numbers such that

where  ,
,  and
and  are sequences of real numbers satisfying the following conditions:
are sequences of real numbers satisfying the following conditions:
-
(i)
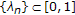 ,
, 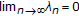 and
and 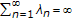 ;
; -
(ii)
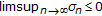 ;
; -
(iii)
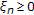 for all
for all 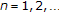 and
and  .
.
Then,  .
.
3. Iterative Algorithm and Convergence Theorem
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  ,
,  a multivalued mapping,
a multivalued mapping,  a contraction mapping with constant
a contraction mapping with constant  , and
, and  an
an  -mapping generated by
-mapping generated by  and
and  , where sequence
, where sequence  is nonexpansive. Let
is nonexpansive. Let  be a sequence in
be a sequence in  and
and  a sequence in
a sequence in  . We can develop Algorithm 3.1 for finding a common element of a set of fixed points of
. We can develop Algorithm 3.1 for finding a common element of a set of fixed points of  -mapping
-mapping  and a set of solutions of GMEP(1.2).
and a set of solutions of GMEP(1.2).
Algorithm.
For given  and
and  , there exist sequences
, there exist sequences  ,
,  in
in  and
and  in
in  such that for all
such that for all  ,
,

We now prove the strong convergence of iterative sequence  ,
,  , and
, and  generated by Algorithm 3.1.
generated by Algorithm 3.1.
Theorem 3.2.
Let  be a nonempty closed convex bounded subset of a real Hilbert space
be a nonempty closed convex bounded subset of a real Hilbert space  ,
,  a multivalued
a multivalued  -Lipschitz continuous mapping with constant
-Lipschitz continuous mapping with constant  ,
,  a contraction mapping with constant
a contraction mapping with constant  . Let
. Let  be a real-valued function satisfying the conditions
be a real-valued function satisfying the conditions  and let
and let  be an equilibrium-like function satisfying conditions
be an equilibrium-like function satisfying conditions  and
and  :
:

 for all
for all  and
and  , where
, where  ,
,  and
and  .
.
Assume that  is a Lipschitz function with Lipschitz constant
is a Lipschitz function with Lipschitz constant  which satisfies the conditions
which satisfies the conditions  . Let
. Let  be an
be an  -strongly convex function with constant
-strongly convex function with constant  which satisfies conditions
which satisfies conditions  and
and  with
with  . Let
. Let  be an
be an  -mapping generated by
-mapping generated by  and
and  and
and  , where sequence
, where sequence  is nonexpansive. Let
is nonexpansive. Let  ,
,  and
and  be sequences generated by Algorithm 3.1, where
be sequences generated by Algorithm 3.1, where  is a sequence in
is a sequence in  and
and  in
in  satisfying the following conditions:
satisfying the following conditions:

 ,
,  and
and  ;
;

 and
and  ;
;

 where
where  .
.
Then the sequences  and
and  converge strongly to
converge strongly to  , and
, and  converges strongly to
converges strongly to  , where
, where  .
.
Proof.
It is easy to see from ( ) that
) that

for all  and
and  , where
, where  ,
,  , and
, and  . All the conclusions (a)–(e) of Lemma 2.4 hold.
. All the conclusions (a)–(e) of Lemma 2.4 hold.
Let  . Then
. Then  is a contraction of
is a contraction of  into itself. In fact,
into itself. In fact,

Hence there exists a unique element  such that
such that  . Noting that
. Noting that  and
and  , we get that
, we get that  .
.
Now, we prove that  and
and  as
as  . Observe that
. Observe that

Noting that  and
and  , it follows from (3.1) that
, it follows from (3.1) that


Putting  in (3.5) and
in (3.5) and  in (3.6), respectively, we have
in (3.6), respectively, we have

Adding up those inequalities, we obtain from (2.5), ( ), and (
), and ( ) that
) that

It follows that

since  and
and  are Lipschitz continuous wiht Lipschitz constants
are Lipschitz continuous wiht Lipschitz constants  and
and  , respectively. Noting that
, respectively. Noting that  , without loss of generality, we assume that there exists a real number
, without loss of generality, we assume that there exists a real number  such that
such that  for all
for all  Thus,
Thus,

which implies that

and hence

where  . Set
. Set  . Combining (3.4) and (3.12) yields
. Combining (3.4) and (3.12) yields

From conditions  and
and  ,
,

Set  and
and

Then Lemmas 2.6 and 2.7 imply that  and
and  is a Cauchy sequence in
is a Cauchy sequence in  . Hence from (3.12), we get
. Hence from (3.12), we get

We know from  that
that  . It follows that
. It follows that

Thus, 
Next, we prove that there exists  , such that
, such that  ,
,  , and
, and  as
as  , where
, where  .
.
Let  . Then
. Then

and so

By the convexity of  , we have
, we have

It follows that

This implies that

Since  is a Cauchy sequence in
is a Cauchy sequence in  , there exists an element
, there exists an element  such that
such that  . Now
. Now  implies that
implies that  . From (3.1), we have
. From (3.1), we have

and for  ,
,


Thus,

By (3.24) and (3.26), we have

It follows that  is a Cauchy sequence in
is a Cauchy sequence in  and so there exists an element
and so there exists an element  in
in  such that
such that  :
:

that is,  . We conclude that
. We conclude that  as
as  .
.
It follows that

and so  , that is,
, that is,  . Since
. Since  and
and  , we know that
, we know that  . From (3.1) and (
. From (3.1) and ( ), we have
), we have

that is,  . Thus,
. Thus,  .
.
Since  , we have
, we have  for all
for all  . From
. From  , we have
, we have

and so

It follows from (3.19) that

Set

Then,  ,
,  , and
, and  . It follows from Lemma 2.8 that
. It follows from Lemma 2.8 that  and so
and so  . This completes the proof.
. This completes the proof.
Remark 3.3.
Theorem 3.2 improves and extends the main results of S. Takahashi and W. Takahashi [12].
We now give some applications of Theorem 3.2. If the set-valued mapping  in Theorem 3.2 is single-valued, then we have the following corollary.
in Theorem 3.2 is single-valued, then we have the following corollary.
Corollary 3.4.
Let  be a nonempty closed convex bounded subset of a real Hilbert space
be a nonempty closed convex bounded subset of a real Hilbert space  ,
,  a Lipschitz continuous mapping with constant
a Lipschitz continuous mapping with constant  ,
,  a contraction mapping with constant
a contraction mapping with constant  . Let
. Let  be a real-valued function satisfying the conditions
be a real-valued function satisfying the conditions  and let
and let  be an equilibrium-like function satisfying the conditions
be an equilibrium-like function satisfying the conditions  and
and  :
:

 for all
for all  and
and  .
.
Assume that  is a Lipschitz function with Lipschitz constant
is a Lipschitz function with Lipschitz constant  which satisfies the conditions
which satisfies the conditions  . Let
. Let  be an
be an  -strongly convex function with constant
-strongly convex function with constant  which satisfies the conditions
which satisfies the conditions  and
and  with
with  . Let
. Let  be an
be an  -mapping generated by
-mapping generated by  and
and  and
and  , where sequence
, where sequence  is nonexpansive. Let
is nonexpansive. Let  ,
,  , and
, and  be sequences generated by
be sequences generated by

where  is a sequence in
is a sequence in  and
and  in
in  satisfying conditions
satisfying conditions  . Then the sequences
. Then the sequences  and
and  converge strongly to
converge strongly to  , where
, where  .
.
Corollary 3.5.
Let  be a nonempty closed convex bounded subset of a real Hilbert space
be a nonempty closed convex bounded subset of a real Hilbert space  ,
,  a multivalued
a multivalued  -Lipschitz continuous mapping with constant
-Lipschitz continuous mapping with constant  ,
,  a contraction mapping with constant
a contraction mapping with constant  . Let
. Let  be a real-valued function satisfying the conditions
be a real-valued function satisfying the conditions  and let
and let  be an equilibrium-like function satisfying the conditions
be an equilibrium-like function satisfying the conditions  and
and  . Assume that
. Assume that  is a Lipschitz function with Lipschitz constant
is a Lipschitz function with Lipschitz constant  which satisfies the conditions
which satisfies the conditions  . Let
. Let  be an
be an  -strongly convex function with constant
-strongly convex function with constant  which satisfies the conditions
which satisfies the conditions  and
and  with
with  . Let
. Let  ,
,  , and
, and  be sequences generated by
be sequences generated by

where  is a sequence in
is a sequence in  and
and  in
in  satisfying conditions
satisfying conditions  and
and  . Then the sequences
. Then the sequences  and
and  converge strongly to
converge strongly to  , and
, and  converges strongly to
converges strongly to  , where
, where  .
.
Proof.
Let  in Theorem 3.2 for
in Theorem 3.2 for  , where
, where  is an identity mapping. Then
is an identity mapping. Then  for
for  Thus, the condition
Thus, the condition  is satisfied. Now Corollary 3.5 follows from Theorem 3.2. This completes the proof.
is satisfied. Now Corollary 3.5 follows from Theorem 3.2. This completes the proof.
References
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994, 63(1–4):123-145.
Huang N-J, Lan H-Y, Teo KL: On the existence and convergence of approximate solutions for equilibrium problems in Banach spaces. Journal of Inequalities and Applications 2007, 2007:-14.
Giannessi F, Maugeri A, Pardalos PM (Eds): Equilibrium Problems: Nonsmooth Optimization and Variational Inequality Models, Nonconvex Optimization and Its Applications. Volume 58. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2001.
Flores-Bazán F: Existence theorems for generalized noncoercive equilibrium problems: the quasi-convex case. SIAM Journal on Optimization 2000, 11(3):675-690.
Mosco U: Implicit variational problems and quasi variational inequalities. In Nonlinear Operators and the Calculus of Variations (Summer School, Univ. Libre Bruxelles, Brussels, 1975), Lecture Notes in Mathematics. Volume 543. Springer, Berlin, Germany; 1976:83-156.
Sahu DR, Wong N-C, Yao J-C: On convergence analysis of an iterative algorithm for finding common solution of generalized mixed equilibrium problems and fixed point problemes. to appear in Mathematical Inequalities & Applications
Peng J-W, Yao J-C: A new hybrid-extragradient method for generalized mixed equilibrium problems, fixed point problems and variational inequality problems. Taiwanese Journal of Mathematics 2008, 12(6):1401-1432.
Peng J-W, Yao J-C: Some new iterative algorithms for generalized mixed equilibrium problems with strict pseudo-contractions and monotone mappings. to appear in Taiwanese Journal of Mathematics
Glowinski R, Lions J-L, Tremolieres R: Numerical Analysis of Variational Inequalities, Studies in Mathematics and Its Applications. Volume 8. North-Holland, Amsterdam, The Netherlands; 1981:xxix+776.
Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000, 241(1):46-55. 10.1006/jmaa.1999.6615
Hirstoaga SA: Iterative selection methods for common fixed point problems. Journal of Mathematical Analysis and Applications 2006, 324(2):1020-1035. 10.1016/j.jmaa.2005.12.064
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007, 331(1):506-515. 10.1016/j.jmaa.2006.08.036
Yao Y, Liou Y-C, Yao J-C: Convergence theorem for equilibrium problems and fixed point problems of infinite family of nonexpansive mappings. Fixed Point Theory and Applications 2007, 2007:-12.
Shimoji K, Takahashi W: Strong convergence to common fixed points of infinite nonexpansive mappings and applications. Taiwanese Journal of Mathematics 2001, 5(2):387-404.
Takahashi W: Nonlinear Functional Analysis. Fixed Point Theory and Its Application. Yokohama, Yokohama, Japan; 2000:iv+276.
Nadler SB Jr.: Multi-valued contraction mappings. Pacific Journal of Mathematics 1969, 30: 475-488.
Osilike MO, Aniagbosor SC: Weak and strong convergence theorems for fixed points of asymptotically nonexpansive mappings. Mathematical and Computer Modelling 2000, 32(10):1181-1191. 10.1016/S0895-7177(00)00199-0
Xu H-K: Iterative algorithms for nonlinear operators. Journal of the London Mathematical Society 2002, 66(1):240-256. 10.1112/S0024610702003332
Acknowledgments
The authors would like to thank the referees very much for their valuable comments and suggestions. This work was supported by the National Natural Science Foundation of China (10671135) and Specialized Research Fund for the Doctoral Program of Higher Education (20060610005).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zeng, WY., Huang, NJ. & Zhao, CW. Viscosity Approximation Methods for Generalized Mixed Equilibrium Problems and Fixed Points of a Sequence of Nonexpansive Mappings. Fixed Point Theory Appl 2008, 714939 (2008). https://doi.org/10.1155/2008/714939
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/714939
 and
and 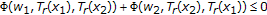 for all
for all 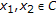 and all
and all 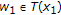 ,
,  , it follows that
, it follows that 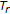 is nonexpansive;
is nonexpansive; for all
for all 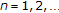 and
and 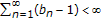 ;
;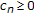 for all
for all 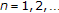 and
and 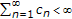 .
.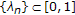 ,
, 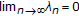 and
and 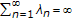 ;
;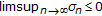 ;
;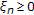 for all
for all 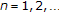 and
and  .
.