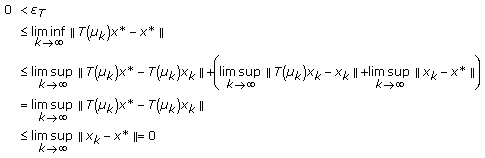- Research Article
- Open access
- Published:
Stability and Convergence Results Based on Fixed Point Theory for a Generalized Viscosity Iterative Scheme
Fixed Point Theory and Applications volume 2009, Article number: 314581 (2009)
Abstract
A generalization of Halpern's iteration is investigated on a compact convex subset of a smooth Banach space. The modified iteration process consists of a combination of a viscosity term, an external sequence, and a continuous nondecreasing function of a distance of points of an external sequence, which is not necessarily related to the solution of Halpern's iteration, a contractive mapping, and a nonexpansive one. The sum of the real coefficient sequences of four of the above terms is not required to be unity at each sample but it is assumed to converge asymptotically to unity. Halpern's iteration solution is proven to converge strongly to a unique fixed point of the asymptotically nonexpansive mapping.
1. Introduction
Fixed point theory is a powerful tool for investigating the convergence of the solutions of iterative discrete processes or that of the solutions of differential equations to fixed points in appropriate convex compact subsets of complete metric spaces or Banach spaces, in general, [1–12]. A key point is that the equations under study are driven by contractive maps or at least by asymptotically nonexpansive maps. By that reason, the fixed point formalism is useful in stability theory to investigate the asymptotic convergence of the solution to stable attractors which are stable equilibrium points. The uniqueness of the fixed point is not required in the most general context although it can be sometimes suitable provided that only one such a point exists in some given problem. Therefore, the theory is useful for stability problems subject to multiple stable equilibrium points. Compared to Lyapunov's stability theory, it may be a more powerful tool in cases when searching a Lyapunov functional is a difficult task or when there exist multiple equilibrium points, [1, 12]. Furthermore, it is not easy to obtain the value of the equilibrium points from that of the Lyapunov functional in the case that the last one is very involved. A generalization of the contraction principle in metric spaces by using continuous nondecreasing functions subject to an inequality-type constraint has been performed in [2]. The concept of  -times reasonable expansive mapping in a complete metric space is defined in [3] and proven to possess a fixed point. In [5], the
-times reasonable expansive mapping in a complete metric space is defined in [3] and proven to possess a fixed point. In [5], the  -stability of Picard's iteration is investigated with
-stability of Picard's iteration is investigated with  being a self-mapping of
being a self-mapping of  where (
where ( ) is a complete metric space. The concept of
) is a complete metric space. The concept of  -stability is set as follows: if a solution sequence converges to an existing fixed point of
-stability is set as follows: if a solution sequence converges to an existing fixed point of  , then the error in terms of distance of any two consecutive values of any solution generated by Picard's iteration converges asymptotically to zero. On the other hand, an important effort has been devoted to the investigation of Halpern's iteration scheme and many associate extensions during the last decades (see, e.g., [4, 6, 9, 10]). Basic Halpern's iteration is driven by an external sequence plus a contractive mapping whose two associate coefficient sequences sum unity for all samples, [9]. Recent extensions of Halpern's iteration to viscosity iterations have been proposed in [4, 6]. In the first reference, a viscosity-type term is added as extraforcing term to the basic external sequence of Halpern's scheme. In the second one, the external driving term is replaced with two ones, namely, a viscosity-type term plus an asymptotically nonexpansive mapping taking values on a left reversible semigroup of asymptotically nonexpansive Lipschitzian mappings on a compact convex subset
, then the error in terms of distance of any two consecutive values of any solution generated by Picard's iteration converges asymptotically to zero. On the other hand, an important effort has been devoted to the investigation of Halpern's iteration scheme and many associate extensions during the last decades (see, e.g., [4, 6, 9, 10]). Basic Halpern's iteration is driven by an external sequence plus a contractive mapping whose two associate coefficient sequences sum unity for all samples, [9]. Recent extensions of Halpern's iteration to viscosity iterations have been proposed in [4, 6]. In the first reference, a viscosity-type term is added as extraforcing term to the basic external sequence of Halpern's scheme. In the second one, the external driving term is replaced with two ones, namely, a viscosity-type term plus an asymptotically nonexpansive mapping taking values on a left reversible semigroup of asymptotically nonexpansive Lipschitzian mappings on a compact convex subset  of the Banach space
of the Banach space  . The final iteration process investigated in [6] consists of three forcing terms, namely, a contraction on
. The final iteration process investigated in [6] consists of three forcing terms, namely, a contraction on  , an asymptotically nonexpansive Lipschitzian mapping taking values in a left reversible semigroup of mappings from a subset of that of bounded functions on its dual. It is proven that the solution converges to a unique common fixed point of all the set asymptotic nonexpansive mappings for any initial conditions on
, an asymptotically nonexpansive Lipschitzian mapping taking values in a left reversible semigroup of mappings from a subset of that of bounded functions on its dual. It is proven that the solution converges to a unique common fixed point of all the set asymptotic nonexpansive mappings for any initial conditions on  . The objective of this paper is to investigate further generalizations for Halpern's iteration process via fixed point theory by using two more driving terms, namely, an external one taking values on
. The objective of this paper is to investigate further generalizations for Halpern's iteration process via fixed point theory by using two more driving terms, namely, an external one taking values on  plus a nonlinear term given by a continuous nondecreasing function, subject to an inequality-type constraint as proposed in [2], whose argument is the distance between pairs of points of sequences in certain complete metric space which are not necessarily directly related to the sequence solution taking values in the subset
plus a nonlinear term given by a continuous nondecreasing function, subject to an inequality-type constraint as proposed in [2], whose argument is the distance between pairs of points of sequences in certain complete metric space which are not necessarily directly related to the sequence solution taking values in the subset  of the Banach space
of the Banach space  . Another generalization point is that the sample-by-sample sum of the scalar coefficient sequences of all the driving terms is not necessarily unity but it converges asymptotically to unity.
. Another generalization point is that the sample-by-sample sum of the scalar coefficient sequences of all the driving terms is not necessarily unity but it converges asymptotically to unity.
2. Stability and Boundedness Properties of a Viscosity-Type Difference Equation
In this section a real difference equation scheme is investigated from a stability point of view by also discussing the existence of stable limiting finite points. The structure of such an iterative scheme supplies the structural basis for the general viscosity iterative scheme later discussed formally in Section 4 in the light of contractive and asymptotically nonexpansive mappings in compact convex subsets of Banach spaces. The following well-known iterative scheme is investigated for an iterative scheme which generates real sequences.
Theorem 2.1.
Consider the difference equation:

such that the error sequence  is generated by
is generated by

for all  , where
, where  .
.
Assume that  and
and  are bounded real constants and
are bounded real constants and  ; for all
; for all  . Then, the following properties hold.
. Then, the following properties hold.
-
(i)
The real sequences
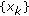 ,
,  , and
, and 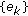 are uniformly bounded if
are uniformly bounded if 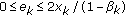 if
if 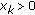 and
and  if
if 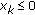 ; for all
; for all  . If, furthermore,
. If, furthermore, 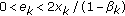 if
if  and
and 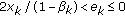 , if
, if  , with
, with 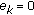 if and only if
if and only if 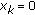 ; for all
; for all 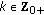 , then the sequences
, then the sequences 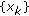 ,
, 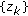 , and
, and 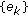 converge asymptotically to the zero equilibrium point as
converge asymptotically to the zero equilibrium point as 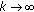 and
and 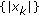 is monotonically decreasing.
is monotonically decreasing. -
(ii)
Let the real sequence
 be defined by
be defined by 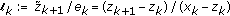 if
if 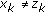 and
and  if
if 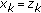 (what implies that
(what implies that 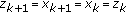 from (2.1) and
from (2.1) and 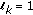 ). Then,
). Then, 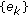 is uniformly bounded if
is uniformly bounded if  ; for all
; for all 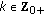 . If, furthermore,
. If, furthermore,  ; for all
; for all  then
then 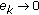 as
as 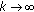 .
. -
(iii)
Let
 and let
and let 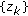 a positive real sequence (i.e., all its elements are nonnegative real constants). Define
a positive real sequence (i.e., all its elements are nonnegative real constants). Define 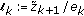 if
if  and
and 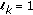 if
if 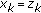 . Then,
. Then, 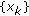 is a positive real sequence and
is a positive real sequence and 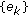 is uniformly bounded if
is uniformly bounded if 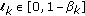 ; for all
; for all 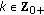 . If, furthermore,
. If, furthermore, 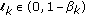 ; for all
; for all 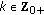 , then
, then 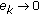 as
as 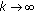 .
. -
(iv)
If
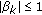 ; for all
; for all 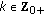 and
and 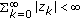 , then
, then 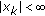 ; for all
; for all 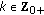 . If
. If  and
and 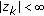 ; for all
; for all 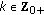 , then
, then 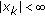 ; for all
; for all 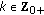 . If
. If  and
and 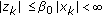 ; for all
; for all 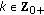 for some
for some 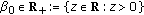 , with
, with  , then
, then  ; for all
; for all  and
and  as
as 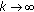 .
. -
(v)
(Corollary to Venter's theorem, [7]). Assume that
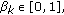 for all
for all  ,
, 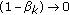 as
as  and
and 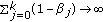 (what imply
(what imply 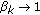 as
as 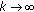 and the sequence
and the sequence 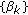 has only a finite set of unity values). Assume also that
has only a finite set of unity values). Assume also that 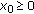 and
and 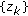 is a nonnegative real sequence with
is a nonnegative real sequence with  . Then
. Then 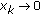 as
as 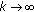 .
. -
(vi)
(Suzuki [8]; see also Saeidi [6]). Let
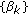 be a sequence in
be a sequence in 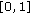 with
with 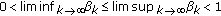 , and let
, and let 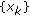 and
and 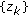 be bounded sequences. Then,
be bounded sequences. Then, 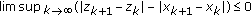 .
. -
(vii)
(Halpern [9]; see Hu [4]). Let
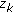 be
be 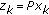 ; for all
; for all  in (2.1) subject to
in (2.1) subject to 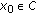 ,
, 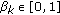 ; for all
; for all 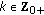 with
with 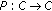 being a nonexpansive self-mapping on
being a nonexpansive self-mapping on  . Thus,
. Thus,  converges weakly to a fixed point of
converges weakly to a fixed point of 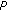 in the framework of Hilbert spaces endowed with the inner product
in the framework of Hilbert spaces endowed with the inner product  , for all
, for all 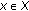 , if
, if  for any
for any 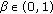 .
.
Proof.
-
(i)
Direct calculations with (2.1) lead to
 (2.3)
(2.3)
so that  if
if  , and equivalently, if
, and equivalently, if  and
and  with
with  , and
, and

Thus,  ,
,  and
and  . If, in addition,
. If, in addition,  and
and  with
with  then
then  and
and  is a monotonically decreasing sequence,
is a monotonically decreasing sequence,  and
and  as
as  . Property (i) has been proven.
. Property (i) has been proven.
-
(ii)
Direct calculations with (2.2) yield for
 ,
, 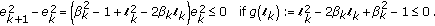 (2.5)
(2.5)
Since  is a convex parabola
is a convex parabola  for all
for all  if real constants
if real constants  exist such that
exist such that  ;
;  . The parabola zeros are
. The parabola zeros are  so that
so that  if
if  . If
. If  , then
, then  with
with  . Thus,
. Thus,  if
if  , for all
, for all  . If
. If  , then
, then  as
as  . Property (ii) has been proven.
. Property (ii) has been proven.
-
(iii)
If
 is positive then
is positive then 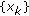 is positive from direct calculations through (2.1). The second part follows directly from Property (ii) by restricting
is positive from direct calculations through (2.1). The second part follows directly from Property (ii) by restricting  for uniform boundedness of
for uniform boundedness of 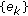 and
and 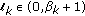 for its asymptotic convergence to zero in the case of nonzero
for its asymptotic convergence to zero in the case of nonzero  .
. -
(iv)
If
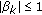 ; for all
; for all 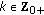 and
and 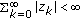 , then from recursive evaluation of (2.1):
, then from recursive evaluation of (2.1):  (2.6)
(2.6)
If,  and
and  ; for all
; for all  , then
, then

If  and
and  , for all
, for all  for some
for some  , then
, then  , for all
, for all  ; thus,
; thus,  is monotonically strictly decreasing so that it converges asymptotically to zero.
is monotonically strictly decreasing so that it converges asymptotically to zero.
Equation (2.1) under the form

with  and
and  being a nonexpansive self-mapping on
being a nonexpansive self-mapping on  under the weak or strong convergence conditions of Theorem 2.1(vii) is known as Halpern's iteration [4], which is a particular case of the generalized viscosity iterative scheme studied in the subsequent sections. Theorem 2.1(vi) extends stability Venter's theorem which is useful in recursive stochastic estimation theory when investigating the asymptotic expectation of the norm-squared parametrical estimation error [7]. Note that the stability result of this section has been derived by using discrete Lyapunov's stability theorem with Lyapunov's sequence
under the weak or strong convergence conditions of Theorem 2.1(vii) is known as Halpern's iteration [4], which is a particular case of the generalized viscosity iterative scheme studied in the subsequent sections. Theorem 2.1(vi) extends stability Venter's theorem which is useful in recursive stochastic estimation theory when investigating the asymptotic expectation of the norm-squared parametrical estimation error [7]. Note that the stability result of this section has been derived by using discrete Lyapunov's stability theorem with Lyapunov's sequence  what guarantees global asymptotic stability to the zero equilibrium point if it is strictly monotonically decreasing on
what guarantees global asymptotic stability to the zero equilibrium point if it is strictly monotonically decreasing on  and to global stability (stated essentially in terms of uniform boundedness of the sequence
and to global stability (stated essentially in terms of uniform boundedness of the sequence  ) if it is monotonically decreasing on
) if it is monotonically decreasing on  . The links between Lyapunov's stability and fixed point theory are clear (see, e.g., [1, 2]). However, fixed point theory is a more powerful tool in the case of uncertain problems since it copes more easily with the existence of multiple stable equilibrium points and with nonlinear mappings. Note that the results of Theorem 2.1 may be further formalized in the context of fixed point theory by defining a complete metric space
. The links between Lyapunov's stability and fixed point theory are clear (see, e.g., [1, 2]). However, fixed point theory is a more powerful tool in the case of uncertain problems since it copes more easily with the existence of multiple stable equilibrium points and with nonlinear mappings. Note that the results of Theorem 2.1 may be further formalized in the context of fixed point theory by defining a complete metric space  , respectively,
, respectively,  for the particular results being applicable to a positive system under nonnegative initial conditions, with the Euclidean metrics defined by
for the particular results being applicable to a positive system under nonnegative initial conditions, with the Euclidean metrics defined by  .
.
3. Some Definitions and Background as Preparatory Tools for Section 4
The four subsequent definitions are then used in the results established and proven in Section 4.
Definition 3.1.
 is a left reversible semigroup if
is a left reversible semigroup if  ; for all
; for all  .
.
It is possible to define a partial preordering relation " " by
" by  ; for all
; for all  for any semigroup
for any semigroup  . Thus,
. Thus,  , for some existing
, for some existing and
and  , such that
, such that  if
if  is left reversible. The semigroup
is left reversible. The semigroup  is said to be left-amenable if it has a left-invariant mean and it is then left reversible, [6, 13].
is said to be left-amenable if it has a left-invariant mean and it is then left reversible, [6, 13].
 is said to be a representation of a left reversible semigroup
is said to be a representation of a left reversible semigroup  as Lipschitzian mappings on
as Lipschitzian mappings on  if
if  is a Lipschitzian mapping on
is a Lipschitzian mapping on  with Lipschitz constant
with Lipschitz constant  and, furthermore,
and, furthermore,  ; for all
; for all  .
.
The representation  may be nonexpansive, asymptotically nonexpansive, contractive and asymptotically contractive according to Definitions 3.3 and 3.4 which follow.
may be nonexpansive, asymptotically nonexpansive, contractive and asymptotically contractive according to Definitions 3.3 and 3.4 which follow.
Definition 3.3.
A representation  of a left reversible semigroup
of a left reversible semigroup  as Lipschitzian mappings on
as Lipschitzian mappings on  , a nonempty weakly compact convex subset of
, a nonempty weakly compact convex subset of  , with Lipschitz constants
, with Lipschitz constants  is said to be a nonexpansive (resp., asymptotically nonexpansive, [6]) semigroup on
is said to be a nonexpansive (resp., asymptotically nonexpansive, [6]) semigroup on  if it holds the uniform Lipschitzian condition
if it holds the uniform Lipschitzian condition  (resp.,
(resp.,  ) on the Lipschitz constants.
) on the Lipschitz constants.
Definition 3.4.
A representation  of a left reversible semigroup
of a left reversible semigroup  as Lipschitzian mappings on
as Lipschitzian mappings on  with Lipschitz constants
with Lipschitz constants  is said to be a contractive (resp., asymptotically contractive) semigroup on
is said to be a contractive (resp., asymptotically contractive) semigroup on  if it holds the uniform Lipschitzian condition
if it holds the uniform Lipschitzian condition  (resp.,
(resp.,  ) on the Lipschitz constants.
) on the Lipschitz constants.
The iteration process (3.1) is subject to a forcing term generated by a set of Lipschitzian mappings  where
where  is a sequence of means on
is a sequence of means on  , with the subset
, with the subset  (defined in Definition 3.5 below) containing unity, where
(defined in Definition 3.5 below) containing unity, where  is the Banach space of all bounded functions on
is the Banach space of all bounded functions on  endowed with the supremum norm, such that
endowed with the supremum norm, such that  where
where  is the dual of
is the dual of  .
.
Definition 3.5.
The real sequence  is a sequence of means on
is a sequence of means on  if
if  .
.
Some particular characterizations of sequences of means to be invoked later on in the results of Section 4 are now given in the definitions which follow.
Definition 3.6.
The sequence of means  on
on  is
is
(1)left invariant if  ; for all
; for all  , for all
, for all  , for all
, for all  in
in  for
for  ;
;
(2)strongly left regular if  , for all
, for all  , where
, where  is the adjoint operator of
is the adjoint operator of  defined by
defined by  ; for all
; for all  , for all
, for all  .
.
Parallel definitions follow for right-invariant and strongly right-amenable sequences of means.  is said to be left (resp., right)-amenable if it has a left (resp., right)-invariant mean. A general viscosity iteration process considered in [6] is the following:
is said to be left (resp., right)-amenable if it has a left (resp., right)-invariant mean. A general viscosity iteration process considered in [6] is the following:

where
(i)the real sequences  ,
,  , and
, and  have elements in
have elements in  of sum being identity, for all
of sum being identity, for all  ;
;
(ii) is a representation of a left reversible semigroup with identity
is a representation of a left reversible semigroup with identity  being asymptotically nonexpansive, on a compact convex subset
being asymptotically nonexpansive, on a compact convex subset  of a smooth Banach space, with respect to a left-regular sequence of means defined on an appropriate invariant subspace of
of a smooth Banach space, with respect to a left-regular sequence of means defined on an appropriate invariant subspace of  ;
;
(iii) is a contraction on
is a contraction on  .
.
It has been proven that the solution of the sequence converges strongly to a unique common fixed point of the representation  which is the solution of a variational inequality [6]. The viscosity iteration process (3.1) generalizes that proposed in [13] for
which is the solution of a variational inequality [6]. The viscosity iteration process (3.1) generalizes that proposed in [13] for  and
and  and also that proposed in [14, 15] with
and also that proposed in [14, 15] with  ,
,  and
and  ; for all
; for all  . Halpern's iteration is obtained by replacing
. Halpern's iteration is obtained by replacing  and
and  in (3.1) by using the formalism of Hilbert spaces, for all
in (3.1) by using the formalism of Hilbert spaces, for all  (see, e.g., [4, 9, 10]). There has been proven the weak convergence of the sequence
(see, e.g., [4, 9, 10]). There has been proven the weak convergence of the sequence  to a fixed point of
to a fixed point of  for any given
for any given  if
if  for
for  [9], also proven to converge strongly to one such a point if
[9], also proven to converge strongly to one such a point if  and
and  as
as  , and
, and  [10]. On the other hand, note that if
[10]. On the other hand, note that if  ,
,  , and
, and  with
with  , for all
, for all  , then the resulting particular iteration process (3.1) becomes the difference equation (2.1) discussed in Theorem 2.1 from a stability point of view provided that the boundedness of the solution is ensured on some convex compact set
, then the resulting particular iteration process (3.1) becomes the difference equation (2.1) discussed in Theorem 2.1 from a stability point of view provided that the boundedness of the solution is ensured on some convex compact set  ; for all
; for all  .
.
4. Boundedness and Convergence Properties of a More General Difference Equation
The viscosity iteration process (3.1) is generalized in this section by including two more forcing terms not being directly related to the solution sequence. One of them being dependent on a nondecreasing distance-valued function related to a complete metric space while the other forcing term is governed by an external sequence  . Furthermore the sum of the four terms of the scalar sequences
. Furthermore the sum of the four terms of the scalar sequences  ,
,  , and
, and  and
and  at each sample is not necessarily unity but it is asymptotically convergent to unity.
at each sample is not necessarily unity but it is asymptotically convergent to unity.
The following generalized viscosity iterative scheme, which is a more general difference equation than (3.1), is considered in the sequel

for all  for a sequence of given finite numbers
for a sequence of given finite numbers  with
with  (if
(if  , then the corresponding sum is dropped off) which can be rewritten as (2.1) if
, then the corresponding sum is dropped off) which can be rewritten as (2.1) if  ; for all
; for all  (except possibly for a finite number of values of the sequence
(except possibly for a finite number of values of the sequence  what implies
what implies  ) by defining the sequence
) by defining the sequence

with  , where
, where
(i) is a strongly left-regular sequence of means on
is a strongly left-regular sequence of means on  , that is,
, that is,  . See Definition 3.5;
. See Definition 3.5;
(ii) is a left reversible semigroup represented as Lipschitzian mappings on
is a left reversible semigroup represented as Lipschitzian mappings on  by
by  .
.
The iterative scheme is subject to the following assumptions.
Assumption 1.
( )
)  ,
,  , and
, and  are real sequences in
are real sequences in  ,
,  is a real sequence in
is a real sequence in  , and
, and  are sequences in
are sequences in  , for all
, for all  for some given
for some given  and
and  .
.
( )
)  ,
,  .
.
( )
)  .
.
( )
)  .
.
( )
)  ; for all
; for all  with
with  being a bounded real sequence satisfying
being a bounded real sequence satisfying  and
and  .
.
( )
)  is a contraction on a nonempty compact convex subset
is a contraction on a nonempty compact convex subset  , of diameter
, of diameter  of a Banach space
of a Banach space  , of topological dual
, of topological dual  , which is smooth, that is, its normalized duality mapping
, which is smooth, that is, its normalized duality mapping  from
from  into the family of nonempty (by the Hahn-Banach theorem [6, 11]), weak-star compact convex subsets of
into the family of nonempty (by the Hahn-Banach theorem [6, 11]), weak-star compact convex subsets of  , defined by
, defined by

is single valued.
( ) The representation
) The representation  of the left reversible semigroup
of the left reversible semigroup  with identity is asymptotically nonexpansive on
with identity is asymptotically nonexpansive on  (see Definition 3.3) with respect to
(see Definition 3.3) with respect to  , with
, with  which is strongly left regular so that it fulfils
which is strongly left regular so that it fulfils  .
.
( )
)  .
.
( )
)  is a complete metric space and
is a complete metric space and  is a self-mapping satisfying the inequality
is a self-mapping satisfying the inequality

where  , for all
, for all  are continuous monotone nondecreasing functions satisfying
are continuous monotone nondecreasing functions satisfying  if and only if
if and only if  ; for all
; for all  .
.
( )
)  is a sequence in
is a sequence in  generated as
generated as  ,
,  with
with  and
and  is a finite given number.
is a finite given number.
Note that Assumption 1( ) is stronger than the conditions imposed on the sequence
) is stronger than the conditions imposed on the sequence  in Theorem 2.1 for (2.1). However, the whole viscosity iteration is much more general than the iterative equation (2.1). Three generalizations compared to existing schemes of this class are that an extracoefficient sequence
in Theorem 2.1 for (2.1). However, the whole viscosity iteration is much more general than the iterative equation (2.1). Three generalizations compared to existing schemes of this class are that an extracoefficient sequence  is added to the set of usual coefficient sequences and that the exact constraint for the sum of coefficients
is added to the set of usual coefficient sequences and that the exact constraint for the sum of coefficients  being unity for all
being unity for all  is replaced by a limit-type constraint
is replaced by a limit-type constraint  as
as  while during the transient such a constraint can exceed unity or be below unity at each sample (see Assumption 1(
while during the transient such a constraint can exceed unity or be below unity at each sample (see Assumption 1( ). Another generalization is the inclusion of a nonnegative term with generalized contractive mapping
). Another generalization is the inclusion of a nonnegative term with generalized contractive mapping  involving another iterative scheme evolving on another, and in general distinct, complete metric space
involving another iterative scheme evolving on another, and in general distinct, complete metric space  (see Assumptions 1(
(see Assumptions 1( ) and 1(
) and 1( ). Some boundedness and convergence properties of the iterative process (4.1) are formulated and proven in the subsequent result.
). Some boundedness and convergence properties of the iterative process (4.1) are formulated and proven in the subsequent result.
Theorem 4.1.
The difference iterative scheme (4.1) and equivalently the difference equation (2.1) subject to (4.2) possess the following properties under Assumption 1.
(i) . Also,
. Also,  and
and  for any norm defined on the smooth Banach space
for any norm defined on the smooth Banach space  and there exists a nonempty bounded compact convex set
and there exists a nonempty bounded compact convex set  such that the solution of (4.2) is permanent in
such that the solution of (4.2) is permanent in  , for all
, for all  and some sufficiently large finite
and some sufficiently large finite  with
with  .
.
(ii) and
and  as
as  .
.
-
(iii)
 (4.5)
(4.5)
(iv)Assume that  such that each sequence element
such that each sequence element  (the first closed orthant of
(the first closed orthant of  ); for all
); for all  , for some
, for some  so that (4.1) is a positive viscosity iteration scheme. Then,
so that (4.1) is a positive viscosity iteration scheme. Then,
(iv.1) is a nonnegative sequence (i.e., all its components are nonnegative for all
is a nonnegative sequence (i.e., all its components are nonnegative for all  , for all
, for all  ), denoted as
), denoted as  ; for all
; for all  .
.
(iv.2)Property (i) holds for  and Property (ii) also holds for a limiting point
and Property (ii) also holds for a limiting point  .
.
(iv.3)Property (iii) becomes

what implies that either

or

Proof.
From (4.2) and substituting the real sequence  from the constraint Assumption 1(
from the constraint Assumption 1( ), we have the following:
), we have the following:

Thus,

where  is an arbitrary finite sufficiently large integer, and
is an arbitrary finite sufficiently large integer, and

since the functions  are continuous on
are continuous on  with
with  and
and  as
as  , [2] with
, [2] with  being prefixed and arbitrarily small. The constants
being prefixed and arbitrarily small. The constants  and
and  are finite for sufficiently large
are finite for sufficiently large  since
since  (Assumption 1(
(Assumption 1( ),
),  is a contraction on
is a contraction on  (Assumption 1(
(Assumption 1( ), and
), and  is a self-mapping on
is a self-mapping on  satisfying Assumption 1(
satisfying Assumption 1( ). Since
). Since  ,
,  and
and  as
as  from Assumptions 1(
from Assumptions 1( ) and 1(
) and 1( ) and
) and  is finite,
is finite,  as
as  and
and  ; for all
; for all  being arbitrarily small since
being arbitrarily small since  is arbitrarily large. Since from Assumption 1(
is arbitrarily large. Since from Assumption 1( ),
),  is an asymptotically nonexpansive semigroup on
is an asymptotically nonexpansive semigroup on  , and
, and  ,
,  , and
, and  as
as  :
:

with  as
as  . One gets from (4.12) into (4.10),
. One gets from (4.12) into (4.10),

what implies that

(see [8]) since  as
as  since
since  is in
is in  and
and  is a strongly left-regular sequence of means on
is a strongly left-regular sequence of means on  such that
such that  ; furthermore,
; furthermore,  ,
,  ,
,  ,
,  ,
,  as
as  and
and  as
as  . Thus, from (4.14) and using the above technical result in [8] for difference equations of the class (2.1) (see also [2]), it follows that
. Thus, from (4.14) and using the above technical result in [8] for difference equations of the class (2.1) (see also [2]), it follows that

since  from Assumption 1(
from Assumption 1( ) since
) since  ,
,  , and
, and  as
as  . From (4.1),
. From (4.1),

so that

Using Assumption 1 and using (4.15) into (4.17) yield

since  ,
,  ,
,  ,
,  as
as  . Also, it follows that
. Also, it follows that  as
as  from (4.15) and (4.18). Note that it has not been proven yet that the sequences
from (4.15) and (4.18). Note that it has not been proven yet that the sequences  and
and  converge to a finite limit as
converge to a finite limit as  since it has not been proven that they are bounded. Thus, the four sequences
since it has not been proven that they are bounded. Thus, the four sequences  and
and  converge asymptotically to the same finite or infinite real limit. Proceed recursively with the solution of (4.1). Thus, for a given sufficiently large finite
converge asymptotically to the same finite or infinite real limit. Proceed recursively with the solution of (4.1). Thus, for a given sufficiently large finite  and for all
and for all  , one gets
, one gets


for all  , for some positive real sequences
, for some positive real sequences ,
,  , and
, and  satisfying
satisfying  and
and  ,
,  and
and  as
as  with
with  and
and  being arbitrarily small for sufficiently large
being arbitrarily small for sufficiently large  , and
, and

for sufficiently large  and a sufficiently small
and a sufficiently small  which exists from Assumptions 1(
which exists from Assumptions 1( ) and 1(
) and 1( ). Note that the sequences
). Note that the sequences  and
and  may be chosen to satisfy
may be chosen to satisfy  and
and  ; for all
; for all  . Now, proceed by complete induction by assuming that
. Now, proceed by complete induction by assuming that  for given sufficiently large
for given sufficiently large  and finite
and finite  . Then, one gets from (4.20) that
. Then, one gets from (4.20) that  for any prescribed
for any prescribed  if
if

with  and
and  which always holds for sufficiently large finite
which always holds for sufficiently large finite  since
since  as
as  . It has been proven by complete induction that the first part of Property (i) holds with the set
. It has been proven by complete induction that the first part of Property (i) holds with the set  being built such that
being built such that  for the given initial condition
for the given initial condition  . For a set of initial conditions
. For a set of initial conditions  with any set
with any set  convex and bounded, a common set
convex and bounded, a common set  might be defined for any initial condition of (4.1) in
might be defined for any initial condition of (4.1) in  with a redefinition of the constant
with a redefinition of the constant  as
as  . The second part of Property (i) follows for any norm on
. The second part of Property (i) follows for any norm on  from the property of equivalence of norms. Furthermore, the real sequences
from the property of equivalence of norms. Furthermore, the real sequences  and
and  converge strongly to a finite limit in
converge strongly to a finite limit in  since they are uniformly bounded so that Property (ii) has also been proven. Property (iii) follows directly from (4.1) and Property (ii). Property (iv.
since they are uniformly bounded so that Property (ii) has also been proven. Property (iii) follows directly from (4.1) and Property (ii). Property (iv. ) follows since
) follows since  is a nonnegative
is a nonnegative  -vector sequence provided that
-vector sequence provided that  if
if  what follows from simple inspection of (4.1). Properties (iv.
what follows from simple inspection of (4.1). Properties (iv. )-(iv.
)-(iv. ) follow directly from separating nonnegative positive and nonpositive terms in the right-hand side of the expression in Property (iii).
) follow directly from separating nonnegative positive and nonpositive terms in the right-hand side of the expression in Property (iii).
The convergence properties of Theorem 4.1(ii) are now related to the limits being fixed points of the asymptotically nonexpansive semigroup  which is the representation as Lipschitzian mappings on
which is the representation as Lipschitzian mappings on  of a left reversible semigroup
of a left reversible semigroup  with identity.
with identity.
Theorem 4.2.
The following properties hold.
-
(i)
Let
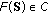 be the set of fixed points of the asymptotically nonexpansive semigroup
be the set of fixed points of the asymptotically nonexpansive semigroup 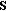 on
on 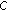 . Then, the common strong limit
. Then, the common strong limit 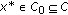 of the sequences
of the sequences 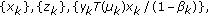 and
and  in Theorem 4.1(ii) is a fixed point of
in Theorem 4.1(ii) is a fixed point of 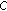 located in
located in 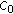 and, thus, a stable equilibrium point of the iterative scheme (4.1) provided that
and, thus, a stable equilibrium point of the iterative scheme (4.1) provided that 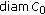 , and then
, and then 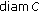 , is sufficiently large.
, is sufficiently large.
(ii) .
.
Proof.
-
(i)
Proceed by contradiction by assuming that
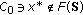 so that there exists
so that there exists  such that
such that 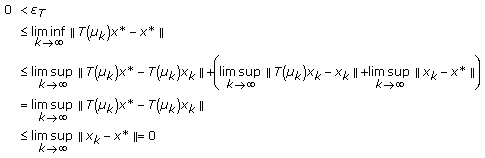 (4.23)
(4.23)
since  , where the above two limits exist and are zero from Theorem 4.1(ii). Then,
, where the above two limits exist and are zero from Theorem 4.1(ii). Then,  , with
, with  being nonempty since, at least one such finite fixed point exists in
being nonempty since, at least one such finite fixed point exists in  .
.
Property (ii) follows directly from Theorem 4.1(iii)-(iv).
Remark 4.3.
Note that the boundedness property of Theorem 4.1(i) does not require explicitly the condition of Assumption 1( ) that
) that  is asymptotically nonexpansive. On the other hand, neither Theorem 4.1 nor Theorem 4.2 requires Assumption 1(
is asymptotically nonexpansive. On the other hand, neither Theorem 4.1 nor Theorem 4.2 requires Assumption 1( ).
).
Definition 4.4 (see [8]).
Let the sequence of means  be in
be in  , and let
, and let  be a representation of a left reversible semigroup
be a representation of a left reversible semigroup  . Then
. Then  is
is  -stable if the functions
-stable if the functions  and
and  on
on  are also in
are also in  ; for all
; for all  , for all
, for all  .
.
Let  and
and  be convex subsets of the Banach space
be convex subsets of the Banach space  , with
, with  under proper inclusion, and let
under proper inclusion, and let  be a retraction of
be a retraction of  onto
onto  . Then
. Then  is said to be sunny if
is said to be sunny if  ; for all
; for all  , for all
, for all  provided that
provided that  .
.
Definition 4.6.
 is said t be a sunny nonexpansive retract of
is said t be a sunny nonexpansive retract of  if there exists a sunny nonexpansive retraction
if there exists a sunny nonexpansive retraction  of
of  onto
onto  .
.
It is known that if  is weakly compact,
is weakly compact,  is a mean on
is a mean on  (see Definition 3.5), and
(see Definition 3.5), and  is in
is in  for each
for each  , then there is a unique
, then there is a unique  such that
such that  for each
for each  . Also, if
. Also, if  is smooth, that is, the duality mapping
is smooth, that is, the duality mapping  of
of  is single valued then a retraction
is single valued then a retraction  of
of  onto
onto  is sunny and nonexpansive if and only if
is sunny and nonexpansive if and only if  , for all
, for all  [6, 11].
[6, 11].
Remark 4.7.
Note that Theorem 4.2 proves the convergence to a fixed point in  , with
, with  being constructively proven to be nonempty by first building a sufficiently large convex compact
being constructively proven to be nonempty by first building a sufficiently large convex compact  so that the solution of the iterative scheme (4.1) is always bounded on
so that the solution of the iterative scheme (4.1) is always bounded on  . Note also that Theorems 4.1 and 4.2 need not the assumption of
. Note also that Theorems 4.1 and 4.2 need not the assumption of  being a left-invariant
being a left-invariant  -stable subspace of containing "
-stable subspace of containing " " and to be a left-invariant mean on
" and to be a left-invariant mean on  , although it is assumed to be strongly left regular so that it fulfils
, although it is assumed to be strongly left regular so that it fulfils  ; for all
; for all  (Assumption 1(
(Assumption 1( ), see Definition 3.6. However, the convergence to a unique fixed point in the set
), see Definition 3.6. However, the convergence to a unique fixed point in the set  is not proven under those less stringent assumptions. Note also that Assumption 1(
is not proven under those less stringent assumptions. Note also that Assumption 1( ) required by Theorem 4.1 and also by Theorem 4.2 as a result is one of the two properties associated with the
) required by Theorem 4.1 and also by Theorem 4.2 as a result is one of the two properties associated with the  -stability of
-stability of  .
.
The results of Theorems 4.1 and 4.2 with further considerations by using Definitions 4.4 and 4.5 allow to obtain the convergence to a unique fixed point under more stringent conditions for the semigroup of self-mappings ,
,  as follows.
as follows.
Theorem 4.8.
If Assumption 1 hold and, furthermore,  is a left-invariant
is a left-invariant  -stable subspace of
-stable subspace of  then the sequence
then the sequence  , generated by (4.1), converges strongly to a unique
, generated by (4.1), converges strongly to a unique  ; for all
; for all  , for all
, for all  , for all
, for all  which is the unique solution of the variational inequality
which is the unique solution of the variational inequality  . Equivalently,
. Equivalently,  where
where  is the unique sunny nonexpansive retraction of
is the unique sunny nonexpansive retraction of  onto
onto  .
.
The proof follows under similar tools as those used in [6] since  is a nonempy sunny nonexpansive retract of
is a nonempy sunny nonexpansive retract of  which is unique since
which is unique since  is nonexpansive for all
is nonexpansive for all  .
.
Proof.
Let  be the sequence solution generated by the particular iterative scheme resulting from (4.1) for any initial conditions
be the sequence solution generated by the particular iterative scheme resulting from (4.1) for any initial conditions  when all the functions
when all the functions  and
and  are zeroed. It is obvious by the calculation of the recursive solution of (4.1) from (4.19) that the error from both solutions satisfies
are zeroed. It is obvious by the calculation of the recursive solution of (4.1) from (4.19) that the error from both solutions satisfies

Since the convergence of the solution to fixed points of Theorems 4.1, 4.2, and 4.8 follows also for the sequence  it follows that a unique fixed point exists satisfying
it follows that a unique fixed point exists satisfying

where  is unique since
is unique since  is also unique from Theorem 4.8. Assume that
is also unique from Theorem 4.8. Assume that  with
with  . Then,
. Then,

If  and
and  ; for all
; for all  and the
and the  -functions are zero then both fixed points are related by the constraint
-functions are zero then both fixed points are related by the constraint  . Thus, consider a representation
. Thus, consider a representation  of a left reversible semigroup
of a left reversible semigroup  as Lipschitzian mappings on
as Lipschitzian mappings on  (see Definitions 3.2 and 3.3), a nonempty compact subset of the smooth Banach space
(see Definitions 3.2 and 3.3), a nonempty compact subset of the smooth Banach space  with Lipschitz constants
with Lipschitz constants  which is asymptotically nonexpansive. Consider the iteration scheme:
which is asymptotically nonexpansive. Consider the iteration scheme:


with  , where
, where
(i) is a strongly left-regular sequence of means on
is a strongly left-regular sequence of means on  , that is,
, that is,  (the dual of
(the dual of  ). See Definitions 3.5 and 3.6;
). See Definitions 3.5 and 3.6;
(ii) is a left reversible semigroup represented as Lipschitzian mappings on
is a left reversible semigroup represented as Lipschitzian mappings on  by
by  .
.
Assumption 2.
The iterative scheme (4.27) keeps the applicable parts of Assumptions 1( )–1(
)–1( ), 1(
), 1( ) for the nonidentically zero parameterizing sequences
) for the nonidentically zero parameterizing sequences  ,
,  and
and  . Assumptions 1(
. Assumptions 1( ) and 1(
) and 1( ) are modified with the replacements
) are modified with the replacements  ,
,  , and
, and  .
.
Theorems 4.1 and 4.8 result in the following result for the iterative scheme (4.27) for  ,
,  :
:
Theorem 4.9.
The following properties hold under Assumption 2.
(i) ; for all
; for all  . Also,
. Also,  and
and  for any norm defined on the smooth Banach space
for any norm defined on the smooth Banach space  and there exists a nonempty bounded compact convex set
and there exists a nonempty bounded compact convex set  such that the solution of (4.2) is permanent in
such that the solution of (4.2) is permanent in  , for all
, for all  and some sufficiently large finite
and some sufficiently large finite  with
with  .
.
(ii) and
and  as
as  .
.
(iii)
(iv)Assume that the nonempty convex subset  of the smooth Banach space
of the smooth Banach space  , which contains the sequence
, which contains the sequence  of means on
of means on  , is such that each element
, is such that each element  ; for all
; for all  , for some
, for some  so that (4.1) is a positive viscosity iteration scheme (4.27). Then,
so that (4.1) is a positive viscosity iteration scheme (4.27). Then,
(iv.1) is a nonnegative sequence (i.e., all its components are nonnegative for all
is a nonnegative sequence (i.e., all its components are nonnegative for all  , for all
, for all  ), denoted as
), denoted as  ; for all
; for all  .
.
(iv.2)Property (i) holds for  and Property (ii) also holds for a limiting point
and Property (ii) also holds for a limiting point  .
.
(iv.3)Property (iii) becomes

what implies that either

or

(v)If, furthermore,  is a left-invariant
is a left-invariant  -stable subspace of
-stable subspace of  , then the sequence
, then the sequence  , generated by (4.27), converges strongly to a unique
, generated by (4.27), converges strongly to a unique  ; for all
; for all  , for all
, for all  which is the unique solution of the variational inequality
which is the unique solution of the variational inequality  . Equivalently,
. Equivalently,  where
where  is the unique sunny nonexpansive retraction of
is the unique sunny nonexpansive retraction of  onto
onto  . Furthermore, the unique fixed points of the iterative schemes (4.1) and (4.27) are related by
. Furthermore, the unique fixed points of the iterative schemes (4.1) and (4.27) are related by

If, in addition,  and
and  and the
and the  -functions are identically zero in the iterative scheme (4.1), then
-functions are identically zero in the iterative scheme (4.1), then  .
.
Remark 4.10.
Note that the results of Section 4 generalize those of Section 2 since the iterative process (4.1) possesses simultaneously a nonlinear contraction and a nonexpansive mapping plus terms associated to driving terms combining both external driving forces plus the contribution of a nonlinear function evaluating distances over, in general, distinct metric spaces than that generating the solution of the iteration process. Therefore, the results about fixed points in Theorem 2.1(vi)-(vii) are directly included in Theorem 4.1.
Venter's theorem can be used for the convergence to the equilibrium points of the solutions of the generalized iterative schemes (4.1) and (4.27), provided they are positive, as follows.
Corollary 4.11.
Assume that
( )
)  are both contractive mappings with
are both contractive mappings with  being compact and convex,
being compact and convex,  , such that
, such that  is a left-invariant
is a left-invariant  -stable subspace of
-stable subspace of  with
with  being a left reversible semigroup;
being a left reversible semigroup;
( )
)  , with
, with  being compact and convex,
being compact and convex,  ,
,  ,
,  and
and  ; for all
; for all  for some real constants
for some real constants  , and
, and  if
if  ;
;
( )
)  and
and  .
.
Then, the sets of fixed points of the positive iteration schemes (4.1) and (4.27) contain a common stable equilibrium point  which is a unique solution to the variational equations of Theorems 4.8 and 4.9; that is,
which is a unique solution to the variational equations of Theorems 4.8 and 4.9; that is,  and that
and that  .
.
Outline of Proof
The fact that the mappings  are both contractive,
are both contractive,  and
and  imply that the generated sequences
imply that the generated sequences  ,
,  are both nonnegative and bounded for any
are both nonnegative and bounded for any  and they have unique zero limits from Theorem 2.1(v).
and they have unique zero limits from Theorem 2.1(v).
The following result is obvious since if the representation  is nonexpansive, contractive or asymptotically contractive (Definitions 3.3 and 3.4), then it is also asymptotically nonexpansive as a result.
is nonexpansive, contractive or asymptotically contractive (Definitions 3.3 and 3.4), then it is also asymptotically nonexpansive as a result.
Corollary 4.12.
If the representation  is nonexpansive, contractive or asymptotically contractive, then Theorems 4.1, 4.2, and 4.8 still hold under Assumption 1, and Theorem 4.9 still holds under Assumption 2.
is nonexpansive, contractive or asymptotically contractive, then Theorems 4.1, 4.2, and 4.8 still hold under Assumption 1, and Theorem 4.9 still holds under Assumption 2.
References
Burton TA: Stability by Fixed Point Theory for Functional Differential Equations. Dover Publications, Mineola, NY, USA; 2006:xiv+348.
Dutta PN, Choudhury BS: A generalisation of contraction principle in metric spaces. Fixed Point Theory and Applications 2008, Article ID 406368, 2008:-8.
Chen C, Zhu C: Fixed point theorems for times reasonable expansive mapping. Fixed Point Theory and Applications 2008, Article ID 302617, 2008:-6.
Hu LG: Strong convergence of a modified Halpern's iteration for nonexpansive mappings. Fixed Point Theory and Applications 2008, Article ID 649162, 2008:-9.
Qing Y, Rhoades BE: -stability of Picard iteration in metric spaces. Fixed Point Theory and Applications 2008, Article ID 418971, 2008:-4.
Saeidi S: Approximating common fixed points of Lipschitzian semigroup in smooth Banach spaces. Fixed Point Theory and Applications 2008, Article ID 363257, 2008:-17.
Mendel JM: Discrete Techniques of Parameter Estimation: The Equation Error Formulation. Marcel Dekker, New York, NY, USA; 1973:xiv+385. Control Theory: A Series of Monographs and Textbooks
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals. Journal of Mathematical Analysis and Applications 2005,305(1):227–239. 10.1016/j.jmaa.2004.11.017
Halpern B: Fixed points of nonexpanding maps. Bulletin of the American Mathematical Society 1967, 73: 957–961. 10.1090/S0002-9904-1967-11864-0
Lions PL: Approximation de points fixes de contractions. Comptes Rendus de l'Académie des Sciences, Série A-B 1977,284(21):A1357-A1359.
Aleyner A, Reich S: An explicit construction of sunny nonexpansive retractions in Banach spaces. Fixed Point Theory and Applications 2005,2005(3):295–305. 10.1155/FPTA.2005.295
De la Sen M: About robust stability of dynamic systems with time delays through fixed point theory. Fixed Point Theory and Applications 2008, Article ID 480187, 2008:-20.
Lau ATM, Miyake H, Takahashi W: Approximation of fixed points for amenable semigroups of nonexpansive mappings in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2007,67(4):1211–1225. 10.1016/j.na.2006.07.008
Xu HK: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004,298(1):279–291. 10.1016/j.jmaa.2004.04.059
Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000,241(1):46–55. 10.1006/jmaa.1999.6615
Acknowledgments
The author is very grateful to the Spanish Ministry of Education by its partial support of this work through Grant DPI2006-00714. He is also grateful to the Basque Government by its support through Grants GIC07143-IT-269-07 and SAIOTEK S-PE08UN15. The author is also grateful to the reviewers for their interesting comments which helped him to improve the final version of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
De la Sen, M. Stability and Convergence Results Based on Fixed Point Theory for a Generalized Viscosity Iterative Scheme. Fixed Point Theory Appl 2009, 314581 (2009). https://doi.org/10.1155/2009/314581
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/314581
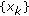 ,
,  , and
, and 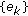 are uniformly bounded if
are uniformly bounded if 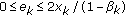 if
if 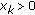 and
and  if
if 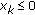 ; for all
; for all  . If, furthermore,
. If, furthermore, 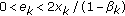 if
if  and
and 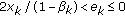 , if
, if  , with
, with 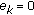 if and only if
if and only if 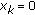 ; for all
; for all 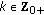 , then the sequences
, then the sequences 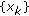 ,
, 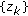 , and
, and 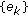 converge asymptotically to the zero equilibrium point as
converge asymptotically to the zero equilibrium point as 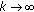 and
and 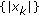 is monotonically decreasing.
is monotonically decreasing. be defined by
be defined by 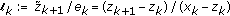 if
if 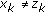 and
and  if
if 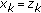 (what implies that
(what implies that 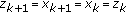 from (2.1) and
from (2.1) and 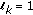 ). Then,
). Then, 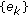 is uniformly bounded if
is uniformly bounded if  ; for all
; for all 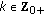 . If, furthermore,
. If, furthermore,  ; for all
; for all  then
then 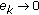 as
as 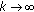 .
. and let
and let 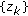 a positive real sequence (i.e., all its elements are nonnegative real constants). Define
a positive real sequence (i.e., all its elements are nonnegative real constants). Define 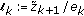 if
if  and
and 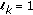 if
if 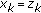 . Then,
. Then, 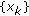 is a positive real sequence and
is a positive real sequence and 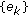 is uniformly bounded if
is uniformly bounded if 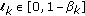 ; for all
; for all 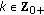 . If, furthermore,
. If, furthermore, 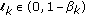 ; for all
; for all 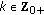 , then
, then 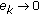 as
as 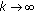 .
.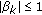 ; for all
; for all 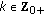 and
and 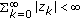 , then
, then 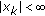 ; for all
; for all 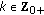 . If
. If  and
and 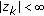 ; for all
; for all 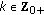 , then
, then 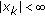 ; for all
; for all 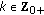 . If
. If  and
and 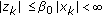 ; for all
; for all 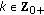 for some
for some 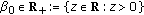 , with
, with  , then
, then  ; for all
; for all  and
and  as
as 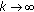 .
.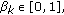 for all
for all  ,
, 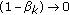 as
as  and
and 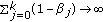 (what imply
(what imply 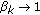 as
as 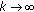 and the sequence
and the sequence 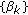 has only a finite set of unity values). Assume also that
has only a finite set of unity values). Assume also that 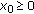 and
and 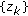 is a nonnegative real sequence with
is a nonnegative real sequence with  . Then
. Then 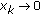 as
as 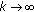 .
.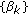 be a sequence in
be a sequence in 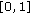 with
with 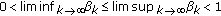 , and let
, and let 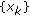 and
and 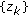 be bounded sequences. Then,
be bounded sequences. Then, 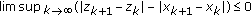 .
.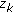 be
be 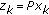 ; for all
; for all  in (2.1) subject to
in (2.1) subject to 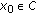 ,
, 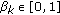 ; for all
; for all 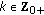 with
with 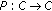 being a nonexpansive self-mapping on
being a nonexpansive self-mapping on  . Thus,
. Thus,  converges weakly to a fixed point of
converges weakly to a fixed point of 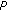 in the framework of Hilbert spaces endowed with the inner product
in the framework of Hilbert spaces endowed with the inner product  , for all
, for all 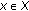 , if
, if  for any
for any 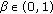 .
.
 ,
, 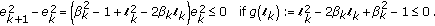
 is positive then
is positive then 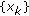 is positive from direct calculations through (2.1). The second part follows directly from Property (ii) by restricting
is positive from direct calculations through (2.1). The second part follows directly from Property (ii) by restricting  for uniform boundedness of
for uniform boundedness of 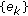 and
and 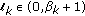 for its asymptotic convergence to zero in the case of nonzero
for its asymptotic convergence to zero in the case of nonzero  .
.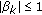 ; for all
; for all 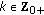 and
and 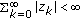 , then from recursive evaluation of (2.1):
, then from recursive evaluation of (2.1): 

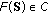 be the set of fixed points of the asymptotically nonexpansive semigroup
be the set of fixed points of the asymptotically nonexpansive semigroup 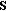 on
on 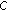 . Then, the common strong limit
. Then, the common strong limit 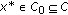 of the sequences
of the sequences 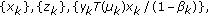 and
and  in Theorem 4.1(ii) is a fixed point of
in Theorem 4.1(ii) is a fixed point of 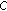 located in
located in 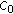 and, thus, a stable equilibrium point of the iterative scheme (4.1) provided that
and, thus, a stable equilibrium point of the iterative scheme (4.1) provided that 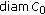 , and then
, and then 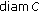 , is sufficiently large.
, is sufficiently large.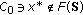 so that there exists
so that there exists  such that
such that