- Research Article
- Open access
- Published:
Some Sufficient Conditions for Fixed Points of Multivalued Nonexpansive Mappings
Fixed Point Theory and Applications volume 2009, Article number: 319804 (2010)
Abstract
We show some sufficient conditions on a Banach space  concerning the generalized James constant, the generalized Jordan-von Neumann constant, the generalized Zbagănu constant, the coefficient
concerning the generalized James constant, the generalized Jordan-von Neumann constant, the generalized Zbagănu constant, the coefficient  , the weakly convergent sequence coefficient WCS(
, the weakly convergent sequence coefficient WCS( ), and the coefficient of weak orthogonality, which imply the existence of fixed points for multivalued nonexpansive mappings. These fixed point theorems improve some previous results in the recent papers.
), and the coefficient of weak orthogonality, which imply the existence of fixed points for multivalued nonexpansive mappings. These fixed point theorems improve some previous results in the recent papers.
1. Introduction
In 1969, Nadler [1] established the multivalued version of Banach contraction principle. Since then the metric fixed point theory of multivalued mappings has been rapidly developed. Some classical fixed point theorems for singlevalued nonexpansive mappings have been extended to multivalued nonexpansive mappings. However, many questions remain open, for instance, the possibility of extending the well-known Kirk's theorem [2], that is, "Do Banach spaces with weak normal structure have the fixed point property (FPP) for multivalued nonexpansive mappings?"
Since weak normal structure is implied by different geometric properties of Banach spaces, it is natural to study whether those properties imply the FPP for multivalued mappings. Dhompongsa et al. [3, 4] introduced the DL condition and property (D) which imply the FPP for multivalued nonexpansive mappings. A possible approach to the above problem is to look for geometric conditions in a Banach space  which imply either the DL condition or property (D). In this setting the following results have been obtained.
which imply either the DL condition or property (D). In this setting the following results have been obtained.
(i)Kaewkhao [5] proved that a Banach space  with
with

satisfies the DL condition. He also showed that the condition

implies the DL condition [6].
(ii)Saejung [7] showed that a Banach space  has property (D) whenever
has property (D) whenever  .
.
In this paper, we show some sufficient conditions on a Banach space  concerning the generalized James constant, the generalized Jordan-von Neumann constant, the generalized Zbăganu constant, the coefficient
concerning the generalized James constant, the generalized Jordan-von Neumann constant, the generalized Zbăganu constant, the coefficient  , the weakly convergent sequence coefficient
, the weakly convergent sequence coefficient  , and the coefficient of weak orthogonality, which imply the existence of fixed points for multivalued nonexpansive mappings. These theorems improve the above results.
, and the coefficient of weak orthogonality, which imply the existence of fixed points for multivalued nonexpansive mappings. These theorems improve the above results.
2. Preliminaries
Before going to the result, let us recall some concepts and results which will be used in the following sections. Let  be a Banach space with the unit ball
be a Banach space with the unit ball  and the unit sphere
and the unit sphere  . The two constants of a Banach space
. The two constants of a Banach space

are called the von Neumann-Jordan [8] and James constants [9], respectively, and are widely studied by many authors [10–20]. Recently, both constants are generalized in the following ways for  (see [12, 13]):
(see [12, 13]):

It is clear that  and
and  .
.
Recently, Gao and Saejung in [6] define a new constant for  :
:

which is inspired by Zbăganu paper [21]. It is clear that

The modulus of convexity of  (see [22]) is a function
(see [22]) is a function  defined by
defined by

The function  is strictly increasing on
is strictly increasing on  . Here
. Here  is the characteristic of convexity of
is the characteristic of convexity of  , and the space is called uniformly nonsquare if
, and the space is called uniformly nonsquare if  .
.
In [23] the author introduces a modulus that scales the 3-dimensional convexity of the unit ball: he considers the number

and defines the function  by
by

He also considers the coefficient corresponding to this modulus:

It is evident that  for all
for all  and in consequence
and in consequence  . Moreover this last inequality can be strict, since it was shown in [23] the existence of Banach spaces with
. Moreover this last inequality can be strict, since it was shown in [23] the existence of Banach spaces with  which are not uniformly nonsquare.
which are not uniformly nonsquare.
The weakly convergent sequence coefficient  of
of  is defined as follows:
is defined as follows:  where the infimum is taken over all weakly null sequences
where the infimum is taken over all weakly null sequences  in
in  such that
such that  and
and  exist.
exist.
The WORTH property was introduced by Sims in [24] as follows. A Banach space  has the WORTH property if
has the WORTH property if

for all  and all weakly null sequences
and all weakly null sequences  . In [25], Jiménez-Melado and Llorens-Fuster defined the coefficient of weak orthogonality, which measures the degree of WORTH wholeness, by
. In [25], Jiménez-Melado and Llorens-Fuster defined the coefficient of weak orthogonality, which measures the degree of WORTH wholeness, by

where the infimum is taken over all  and all weakly null sequence
and all weakly null sequence  . It is known that
. It is known that  has the WORTH property if and only if
has the WORTH property if and only if  .
.
Let  be a nonempty subset of a Banach space
be a nonempty subset of a Banach space  . We shall denote by
. We shall denote by  the family of all nonempty closed bounded subsets of
the family of all nonempty closed bounded subsets of  and by
and by  the family of all nonempty compact convex subsets of
the family of all nonempty compact convex subsets of  . A multivalued mapping
. A multivalued mapping  is said to be nonexpansive if
is said to be nonexpansive if

where  denotes the Hausdorff metric on
denotes the Hausdorff metric on  defined by
defined by

Let  be a bounded sequence in
be a bounded sequence in  . The asymptotic radius
. The asymptotic radius  and the asymptotic center
and the asymptotic center  of
of  in
in  are defined by
are defined by


respectively. It is known that  is a nonempty weakly compact convex set whenever
is a nonempty weakly compact convex set whenever  is.
is.
The sequence  is called regular with respect to
is called regular with respect to  if
if  for all subsequences
for all subsequences  of
of  , and
, and  is called asymptotically uniform with respect to
is called asymptotically uniform with respect to  if
if  for all subsequences
for all subsequences  of
of  .
.
Lemma 2.1.
-
(i)
(See Goebel [26] and Lim [27]) There always exists a subsequence of
 which is regular with respect to
which is regular with respect to 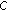 .
. -
(ii)
(See Kirk [28]) If
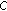 is separable, then
is separable, then 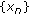 contains a subsequence which is asymptotically uniform with respect to
contains a subsequence which is asymptotically uniform with respect to  .
.
If  is a bounded subset of
is a bounded subset of  , then the Chebyshev radius of
, then the Chebyshev radius of  relative to
relative to  is defined by
is defined by

Dhompongsa et al. [4] introduced the property (D) if there exists  such that for any nonempty weakly compact convex subset
such that for any nonempty weakly compact convex subset  of
of  , any sequence
, any sequence  which is regular asymptotically uniform relative to
which is regular asymptotically uniform relative to  , and any sequence
, and any sequence  which is regular asymptotically uniform relative to
which is regular asymptotically uniform relative to  we have
we have

The Domínguez-Lorenzo condition, DL condition in short form, introduced in [3] is defined as follows: if there exists  such that for every weakly compact convex subset
such that for every weakly compact convex subset  of
of  and for every bounded sequence
and for every bounded sequence  in
in  which is regular with respect to
which is regular with respect to  we have,
we have,

It is clear from the definition that property (D) is weaker than the DL condition. The next results show that property (D) is stronger than weak normal structure and also implies the existence of fixed points for multivalued nonexpansive mappings [4].
Theorem 2.2.
Let  be a Banach space satisfying property (D). Then
be a Banach space satisfying property (D). Then  has weak normal structure.
has weak normal structure.
Theorem 2.3.
Let  be a nonempty weakly compact convex subset of a Banach space
be a nonempty weakly compact convex subset of a Banach space  which satisfies the property (D). Let
which satisfies the property (D). Let  be a nonexpansive mapping, then
be a nonexpansive mapping, then  has a fixed point.
has a fixed point.
3. Main Results
Theorem 3.1.
Let  be a weakly compact convex subset of a Banach space
be a weakly compact convex subset of a Banach space  and let
and let  be a bounded sequence in
be a bounded sequence in  regular with respect to
regular with respect to  . Then for every
. Then for every  ,
,

Proof.
Denote  and
and  . We can assume that
. We can assume that  . By passing to a subsequence if necessary, we can also assume that
. By passing to a subsequence if necessary, we can also assume that  is weakly convergent to a point
is weakly convergent to a point  . Since
. Since  is regular with respect to
is regular with respect to  , then passing through a subsequence does not have any effect to the asymptotic radius of the whole sequence
, then passing through a subsequence does not have any effect to the asymptotic radius of the whole sequence . Let
. Let  , then we have that
, then we have that

Denote  . By the definition of
. By the definition of  we have that
we have that

Convexity of  implies that
implies that  and thus, we obtain
and thus, we obtain

On the other hand, by the weak lower semicontinuity of the norm, we have that

For every  there exists
there exists  such that
such that
(1) ,
,
(2)
(3)
(4)
Now, put  ,
,  and
and  . Using the above estimates, we obtain
. Using the above estimates, we obtain  ,
,  and
and

Thus,

By the weak lower semicontinuity of the norm again, we conclude that  and hence,
and hence,

Therefore  Since the above inequality is true for every
Since the above inequality is true for every  and every
and every  , we obtain
, we obtain

and therefore,

Corollary 3.2.
Let  be a nonempty bounded closed convex subset of a Banach space
be a nonempty bounded closed convex subset of a Banach space  such that
such that  and let
and let  be a nonexpansive mapping. Then
be a nonexpansive mapping. Then  has a fixed point.
has a fixed point.
Proof.
When  , then
, then  satisfies the DL condition by Theorem 3.1. So
satisfies the DL condition by Theorem 3.1. So  has a fixed point by Theorem 2.3.
has a fixed point by Theorem 2.3.
Remark 3.3.
In particular, when  , we get the result of Kaewkhao; a Banach space
, we get the result of Kaewkhao; a Banach space  with
with

satisfies the DL condition.
Theorem 3.4.
Let  be a weakly compact convex subset of a Banach space
be a weakly compact convex subset of a Banach space  and let
and let  be a bounded sequence in
be a bounded sequence in  regular with respect to
regular with respect to  . Then for every
. Then for every  ,
,

Proof.
Let  , and
, and  be as in the proof of the previous theorem. Thus,
be as in the proof of the previous theorem. Thus,

Since  and by the definition of
and by the definition of  , we obtain
, we obtain

On the other hand, by the weak lower semicontinuity of the norm, we have that

For every  , there exists
, there exists  such that
such that
(1)
(2)
(3)
(4)
Now, put  ,
,  and
and  and use the above estimates to obtain
and use the above estimates to obtain  ,
,  ,
,  , and
, and  , so that
, so that

By the definition of  , we get
, we get

Let  ; we obtain that
; we obtain that  . Then we have
. Then we have

This holds for arbitrary  ; hence, we have that
; hence, we have that

Corollary 3.5.
Let  be a nonempty bounded closed convex subset of a Banach space
be a nonempty bounded closed convex subset of a Banach space  such that
such that  and let
and let  be a nonexpansive mapping. Then
be a nonexpansive mapping. Then  has a fixed point.
has a fixed point.
Proof.
When  , then
, then  satisfies the DL condition by Theorem 3.4. So
satisfies the DL condition by Theorem 3.4. So  has a fixed point by Theorem 2.3.
has a fixed point by Theorem 2.3.
Remark 3.6.
In particular, when  , we get the result of Kaewkhao; a Banach space
, we get the result of Kaewkhao; a Banach space  with
with

satisfies the DL condition.
Repeating the arguments in the proof of Theorem 3.4, we can easily get the following conclusion.
Theorem 3.7.
Let  be a nonempty bounded closed convex subset of a Banach space
be a nonempty bounded closed convex subset of a Banach space  such that
such that  and let
and let  be a nonexpansive mapping. Then
be a nonexpansive mapping. Then  has a fixed point.
has a fixed point.
Remark 3.8.
In particular, when  , we get that
, we get that

satisfies the DL condition which improves the result of Kaewkhao; a Banach space  with
with

satisfies the DL condition.
Theorem 3.9.
A Banach space  has property (D) whenever
has property (D) whenever  .
.
Proof.
Let  be a nonempty weakly compact convex subset of
be a nonempty weakly compact convex subset of  . Suppose that
. Suppose that  and
and  are regular asymptotically uniforms relative to
are regular asymptotically uniforms relative to  . Passing to a subsequence, we may assume that
. Passing to a subsequence, we may assume that  is weakly convergent to a point
is weakly convergent to a point  and
and  exists. Let
exists. Let  . Again, passing to a subsequence of
. Again, passing to a subsequence of  , still denoted by
, still denoted by  , we assume in addition that
, we assume in addition that

for all  . Now, put
. Now, put

It is easy to see that  ,
,  ,
,  , and
, and  . This implies that
. This implies that  or
or  Now we estimate
Now we estimate  as follows:
as follows:

Hence,

Remark 3.10.
-
(1)
Theorem 3.9 strengthens the result of Saejung [7] and
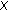 has property (D) whenever
has property (D) whenever 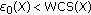 .
. -
(2)
Theorem 3.9 also improves the result
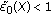 implying that the Banach space
implying that the Banach space 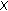 has normal structure from Theorem 2.2.
has normal structure from Theorem 2.2.
References
Nadler SB Jr.: Multi-valued contraction mappings. Pacific Journal of Mathematics 1969, 30: 475–488.
Kirk WA: A fixed point theorem for mappings which do not increase distances. The American Mathematical Monthly 1965, 72: 1004–1006. 10.2307/2313345
Dhompongsa S, Kaewcharoen A, Kaewkhao A: The Domínguez-Lorenzo condition and multivalued nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 2006,64(5):958–970. 10.1016/j.na.2005.05.051
Dhompongsa S, Domínguez Benavides T, Kaewcharoen A, Kaewkhao A, Panyanak B: The Jordan-von Neumann constants and fixed points for multivalued nonexpansive mappings. Journal of Mathematical Analysis and Applications 2006,320(2):916–927. 10.1016/j.jmaa.2005.07.063
Kaewkhao A: The James constant, the Jordan-von Neumann constant, weak orthogonality, and fixed points for multivalued mappings. Journal of Mathematical Analysis and Applications 2007,333(2):950–958. 10.1016/j.jmaa.2006.12.001
Gao J, Saejung S: Normal structure and the generalized James and Zbăganu constants. Nonlinear Analysis: Theory, Methods & Applications 2009,71(7–8):3047–3052. 10.1016/j.na.2009.01.216
Saejung S: Remarks on sufficient conditions for fixed points of multivalued nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 2007,67(5):1649–1653. 10.1016/j.na.2006.07.037
Clarkson JA: The von Neumann-Jordan constant for the Lebesgue spaces. Annals of Mathematics 1937,38(1):114–115. 10.2307/1968512
Gao J, Lau K-S: On two classes of Banach spaces with uniform normal structure. Studia Mathematica 1991,99(1):41–56.
Alonso J, Martín P: A counterexample to a conjecture of G. Zbăganu about the Neumann-Jordan constant. Revue Roumaine de Mathématiques Pures et Appliquées 2006,51(2):135–141.
Yunan C, Zhanfei Z: Geometric properties concerning some parameters. Journal of Natural Science of Heilongjiang University 2008, 6: 711–718.
Dhompongsa S, Piraisangjun P, Saejung S: Generalised Jordan-von Neumann constants and uniform normal structure. Bulletin of the Australian Mathematical Society 2003,67(2):225–240. 10.1017/S0004972700033694
Dhompongsa S, Kaewkhao A, Tasena S: On a generalized James constant. Journal of Mathematical Analysis and Applications 2003,285(2):419–435. 10.1016/S0022-247X(03)00408-6
Jiménez-Melado A, Llorens-Fuster E, Saejung S: The von Neumann-Jordan constant, weak orthogonality and normal structure in Banach spaces. Proceedings of the American Mathematical Society 2006,134(2):355–364.
Saejung S: On James and von Neumann-Jordan constants and sufficient conditions for the fixed point property. Journal of Mathematical Analysis and Applications 2006,323(2):1018–1024. 10.1016/j.jmaa.2005.11.005
Zuo Z, Cui Y: On some parameters and the fixed point property for multivalued nonexpansive mappings. Journal of Mathematical Sciences: Advances and Applications 2008,1(1):183–199.
Zuo Z, Cui Y: A note on the modulus of -convexity and modulus of -convexity. Journal of Inequalities in Pure and Applied Mathematics 2008,9(4):1–7.
Zuo Z, Cui Y: Some modulus and normal structure in Banach space. Journal of Inequalities and Applications 2009, Article ID 676373, 2009:-15.
Zuo Z, Cui Y: A coefficient related to some geometric properties of a Banach space. Journal of Inequalities and Applications 2009, Article ID 934321, 2009:-14.
Zuo Z, Cui Y: The application of generalization modulus of convexity in fixed point theory. Journal of Natural Science of Heilongjiang University 2009, 2: 206–210.
Zbăganu G: An inequality of M. Rădulescu and S. Rădulescu which characterizes the inner product spaces. Revue Roumaine de Mathématiques Pures et Appliquées 2002,47(2):253–257.
Day MM: Normed Linear Spaces, Ergebnisse der Mathematik und Ihrer Grenzgebiete. Volume 2. 3rd edition. Springer, New York, NY, USA; 1973:viii+211.
Jiménez-Melado A: The fixed point property for some uniformly nonoctahedral Banach spaces. Bulletin of the Australian Mathematical Society 1999,59(3):361–367. 10.1017/S0004972700033037
Sims B: Orthogonality and fixed points of nonexpansive maps. In Workshop/Miniconference on Functional Analysis and Optimization (Canberra, 1988), Proceedings of the Centre for Mathematical Analysis, Australian National University. Volume 20. Australian National University, Canberra; 1988:178–186.
Jiménez-Melado A, Llorens-Fuster E: The fixed point property for some uniformly nonsquare Banach spaces. Bollettino della Unione Matemàtica Italiana 1996,10(3):587–595.
Goebel K: On a fixed point theorem for multivalued nonexpansive mappings. Annales Universitatis Mariae Curie-Skłodowska 1975, 29: 69–72.
Lim TC: A fixed point theorem for multivalued nonexpansive mappings in a uniformly convex Banach space. Bulletin of the American Mathematical Society 1974, 80: 1123–1126. 10.1090/S0002-9904-1974-13640-2
Kirk WA: Nonexpansive mappings in product spaces, set-valued mappings and -uniform rotundity. In Nonlinear Functional Analysis and Its Applications, Part 2 (Berkeley, 1983), Proceedings of Symposia in Pure Mathematics. Volume 45. Edited by: Browder FE. American Mathematical Society, Providence, RI, USA; 1986:51–64.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zuo, Z., Cui, Y. Some Sufficient Conditions for Fixed Points of Multivalued Nonexpansive Mappings. Fixed Point Theory Appl 2009, 319804 (2010). https://doi.org/10.1155/2009/319804
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/319804
 which is regular with respect to
which is regular with respect to 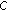 .
.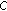 is separable, then
is separable, then 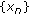 contains a subsequence which is asymptotically uniform with respect to
contains a subsequence which is asymptotically uniform with respect to  .
.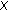 has property (D) whenever
has property (D) whenever 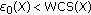 .
.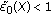 implying that the Banach space
implying that the Banach space 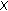 has normal structure from Theorem 2.2.
has normal structure from Theorem 2.2.