- Research Article
- Open access
- Published:
Quasicone Metric Spaces and Generalizations of Caristi Kirk's Theorem
Fixed Point Theory and Applications volume 2009, Article number: 574387 (2009)
Abstract
Cone-valued lower semicontinuous maps are used to generalize Cristi-Kirik's fixed point theorem to Cone metric spaces. The cone under consideration is assumed to be strongly minihedral and normal. First we prove such a type of fixed point theorem in compact cone metric spaces and then generalize to complete cone metric spaces. Some more general results are also obtained in quasicone metric spaces.
1. Introduction and Preliminaries
In 2007, Huang and Zhang [1] introduced the notion of cone metric spaces (CMSs) by replacing real numbers with an ordering Banach space. The authors there gave an example of a function which is contraction in the category of cone metric spaces but not contraction if considered over metric spaces and hence, by proving a fixed point theorem in cone metric spaces, ensured that this map must have a unique fixed point. After that series of articles about cone metric spaces started to appear. Some of those articles dealt with the extension of certain fixed point theorems to cone metric spaces (see, e.g., [2–5]), and some other with the structure of the spaces themselves (see, e.g., [3, 6]). Very recently, some authors have used regular cones to extend some fixed point theorems. For example, in [7] a result about Meir-Keeler type contraction mappings has been extended to regular cone metric spaces. In other works, some results about fixed points of multifunctions on cone metric spaces with normal cones have been obtained as well [8]. For the use of lower semicontinuous functions in obtaining fixed point theorems in cone metric spaces we refer to [9].
In this manuscript, we use cone-valued lower semicontinuous functions to extend some of the results in Caristi [10] and Ekeland [11] to CMS and quasicone metric space (QCMS). The cones under consideration are assumed to be strongly minihedral and normal and hence regular. In particular the cone  in the real line
in the real line  is strongly minihedral and normal; hence the results mentioned in the above references are recovered.
is strongly minihedral and normal; hence the results mentioned in the above references are recovered.
Throughout this paper  stands for a real Banach space. Let
stands for a real Banach space. Let  always be a closed subset of
always be a closed subset of  .
.  is called cone if the following conditions are satisfied:
is called cone if the following conditions are satisfied:
 ,
,
 for all
for all  and non-negative real numbers
and non-negative real numbers  ,
,
 and
and  .
.
For a given cone  , one can define a partial ordering (denoted by
, one can define a partial ordering (denoted by  or
or  ) with respect to
) with respect to  by
by  if and only if
if and only if  . The notation
. The notation  indicates that
indicates that  and
and  while
while  will show
will show  , where
, where  denotes the interior of
denotes the interior of  . From now on, it is assumed that
. From now on, it is assumed that 
The cone  is called
is called
()normal if there is a number  such that for all
such that for all  ,
,

()regular if every increasing sequence which is bounded from above is convergent. That is, if  is a sequence such that
is a sequence such that  for some
for some  , then there is
, then there is  such that
such that  .
.
In  , the least positive integer
, the least positive integer  , satisfying (1.1), is called the normal constant of
, satisfying (1.1), is called the normal constant of  . Note that, in [1, 2], normal constant
. Note that, in [1, 2], normal constant  is stated a positive real number, (
is stated a positive real number, ( ). However, later on and in [2, Lemma
). However, later on and in [2, Lemma  ] it was proved that there is no normal cone with constant
] it was proved that there is no normal cone with constant  .
.
Lemma 1.1.
-
(i)
Every regular cone is normal.
-
(ii)
For each
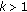 , there is a normal cone with normal constant
, there is a normal cone with normal constant 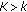 .
. -
(iii)
The cone
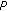 is regular if every decreasing sequence which is bounded from below is convergent.
is regular if every decreasing sequence which is bounded from below is convergent.
The proof of (i) and (ii) were given in [2] and the last one just follows from definition.
Example 1.2 (see [2]).
Let  with the norm
with the norm  , and consider the cone
, and consider the cone 
For each  , put
, put  and
and  Then,
Then,  ,
,  and
and  Since
Since  ,
,  is not normal constant of
is not normal constant of  and hence
and hence  is a nonnormal cone.
is a nonnormal cone.
Definition 1.3.
Let  be a nonempty set. Suppose that the mapping
be a nonempty set. Suppose that the mapping  satisfies the following:
satisfies the following:
() for all
for all  ,
,
() if and only if
if and only if  ,
,
() , for all
, for all  .
.
Then  is said to be a quasicone metric on
is said to be a quasicone metric on  , and the pair
, and the pair  is called a quasicone metric space (QCMS). Additionally, if
is called a quasicone metric space (QCMS). Additionally, if  also satisfies
also satisfies
() for all
for all  ,
,
then  is called a cone metric on
is called a cone metric on  , and the pair
, and the pair  is called a cone metric space (CMS).
is called a cone metric space (CMS).
Example 1.4.
Let  and
and  and
and  . Define
. Define  by
by  , where
, where  are positive constants. Then
are positive constants. Then  is a CMS. Note that the cone
is a CMS. Note that the cone  is normal with the normal constant
is normal with the normal constant 
Definition 1.5.
Let  be a CMS,
be a CMS,  , and let
, and let  be a sequence in
be a sequence in  . Then
. Then
(i) converges to
converges to if for every
if for every  with
with  there is a natural number
there is a natural number  , such that
, such that  for all
for all  . It is denoted by
. It is denoted by  or
or  ;
;
(ii) is a Cauchy sequence if for every
is a Cauchy sequence if for every  with
with  there is a natural number
there is a natural number  , such that
, such that  for all
for all  ;
;
(iii) is a complete cone metric space if every Cauchy sequence in
is a complete cone metric space if every Cauchy sequence in  is convergent in
is convergent in  .
.
Lemma 1.6 (see [1]).
Let  be a CMS, let
be a CMS, let  be a normal cone with normal constant
be a normal cone with normal constant  , and let
, and let  be a sequence in
be a sequence in  . Then,
. Then,
(i)the sequence  converges to
converges to  if and only if d (
if and only if d ( ,
, )
)  0
0  or equivalently
or equivalently  ;
;
(ii)the sequence  is Cauchy if and only if
is Cauchy if and only if  (or equivalently
(or equivalently  );
);
(iii)the sequence  converges to
converges to  and the sequence
and the sequence  converges to
converges to  then
then  .
.
Let  be a CMS over a cone
be a CMS over a cone  in
in  . Thenone has the following.
. Thenone has the following.
(1) and
and  ,
,  .
.
(2)If  , then there exists
, then there exists  such that
such that  implies
implies  .
.
(3)For any given  and
and  there exists
there exists  such that
such that  .
.
(4)If  ,
,  are sequences in
are sequences in  such that
such that  ,
,  and
and  for all
for all  , then
, then  .
.
Definition 1.8 (see [12]).
 is called minihedral cone if
is called minihedral cone if  exists for all
exists for all  , and strongly minihedral if every subset of
, and strongly minihedral if every subset of  which is bounded from above has a supremum.
which is bounded from above has a supremum.
It is easy to see that every strongly minihedral normal cone is regular.
Example 1.9.
Let  with the supremum norm and
with the supremum norm and  Then
Then  is a cone with normal constant
is a cone with normal constant  which is not regular. This is clear, since the sequence
which is not regular. This is clear, since the sequence  is monotonicly decreasing, but not uniformly convergent to
is monotonicly decreasing, but not uniformly convergent to  . Thus,
. Thus,  is not strongly minihedral. It is easy to see that the cone mentioned in Example 1.4 is strongly minihedral.
is not strongly minihedral. It is easy to see that the cone mentioned in Example 1.4 is strongly minihedral.
Definition 1.10 (see [1]).
Let  be a CMS and
be a CMS and  .
.  is said to be sequentially compact if for any sequence
is said to be sequentially compact if for any sequence  in
in  there is a subsequence
there is a subsequence  of
of  such that
such that  is convergent in
is convergent in  .
.
Remark 1.11 (see [6]).
Every cone metric space  is a topological space which is denoted by
is a topological space which is denoted by  . Moreover, a subset
. Moreover, a subset  is sequentially compact if and only if
is sequentially compact if and only if  is compact.
is compact.
2. Main Results
Let  be a CMS,
be a CMS,  , and
, and  a function on
a function on  . Then, the function
. Then, the function  is called a lower semicontinuous (l.s.c) on
is called a lower semicontinuous (l.s.c) on  whenever
whenever

Also, let  be an arbitrary selfmapping on
be an arbitrary selfmapping on  such that
such that

Then,  is called a Caristi map on
is called a Caristi map on  .
.
The following Lemma will be used to prove the next results.
Lemma 2.1.
If  is a decreasing sequence (via the partial ordering obtained by the closed cone
is a decreasing sequence (via the partial ordering obtained by the closed cone  ) such that
) such that  , then
, then 
Proof.
Since  is an increasing sequence,
is an increasing sequence,  , for
, for  and
and  for all
for all  . Then closeness of
. Then closeness of  implies that
implies that  for all
for all  . To see that
. To see that  is the greatest lower bound of
is the greatest lower bound of  , assume that some
, assume that some  satisfies
satisfies  for all
for all  . From
. From  and the closeness of
and the closeness of  we get
we get  or
or  which shows that
which shows that 
Proposition 2.2.
Let  be a compact CMS,
be a compact CMS,  a strongly minihedral cone, and
a strongly minihedral cone, and  a lower semicontinuous
a lower semicontinuous  function. Then,
function. Then,  attains a minimum on
attains a minimum on  .
.
Proof.
Let  which exists by strong minihedrality. For each
which exists by strong minihedrality. For each  , there is an
, there is an  such that
such that  , where
, where  . Since
. Since  is compact, then
is compact, then  has a convergent subsequence. Let
has a convergent subsequence. Let  be this sequence and let
be this sequence and let  .
.
From the definition of lower semicontinuity and Lemma 2.1 it follows that

But then, by the definition of  ,
,  for all
for all  . This completes the proof.
. This completes the proof.
Theorem 2.3.
Let  be a CMS,
be a CMS,  a compact subset of
a compact subset of  ,
,  a strongly minihedral normal cone, and
a strongly minihedral normal cone, and  a lower semicontinuous
a lower semicontinuous  function. Then, each selfmap
function. Then, each selfmap  satisfying (2.2) has a fixed point in
satisfying (2.2) has a fixed point in  .
.
Proof.
By Proposition 2.2,  attains its minimum at some point of
attains its minimum at some point of  , say
, say  . Since
. Since  is the minimum point of
is the minimum point of  , we have
, we have  . By (2.2),
. By (2.2),

Thus,  and so
and so 
The following theorem is an extension of the result of Caristi ([10, Theorem  ]).
]).
Theorem 2.4.
Let  be a complete CMS,
be a complete CMS,  a strongly minihedral normal cone, and
a strongly minihedral normal cone, and  a lower semicontinuous
a lower semicontinuous  function. Then, each selmap
function. Then, each selmap  satisfying (2.2) has a fixed point in
satisfying (2.2) has a fixed point in  .
.
Proof.
Let  have the normal constant
have the normal constant  . Let
. Let  and
and  for all
for all  . Since
. Since  ,
,  and so
and so  .
.
For  , set
, set  and construct a sequence
and construct a sequence  in the following way: let
in the following way: let  be such that
be such that  , where
, where  . Thus, one can observe that
. Thus, one can observe that
(i) ,
,
(ii)
for all  . Note that, (i) implies that the sequence
. Note that, (i) implies that the sequence  is a decreasing sequence in
is a decreasing sequence in  and
and  is regular cone. So, the sequence
is regular cone. So, the sequence  is convergent. Thus, for each
is convergent. Thus, for each  , there exists
, there exists  such that
such that  for all
for all  ,
,  . For
. For  , the triangular inequality implies that
, the triangular inequality implies that

Hence,  . By Lemma 1.6,
. By Lemma 1.6,  yields that the sequence
yields that the sequence  is a Cauchy in
is a Cauchy in  . Completeness of
. Completeness of  implies that the sequence
implies that the sequence  is convergent to some point in
is convergent to some point in  , say
, say 
By (2.5),  and so
and so

for all  . By regarding (2.6), Lemma 1.6, and lower semicontinuity of the function
. By regarding (2.6), Lemma 1.6, and lower semicontinuity of the function  , one can obtain that
, one can obtain that

for all  . Thus,
. Thus,

for all  . Hence,
. Hence,  and it is trivial that
and it is trivial that  for all
for all  . Note that (ii) implies that
. Note that (ii) implies that

Thus,  for all
for all  . On the other hand, by lower semicontinuity of
. On the other hand, by lower semicontinuity of  and (2.9), one can obtain that
and (2.9), one can obtain that

Therefore,  .
.
Since  for each
for each  and
and  , the following inequalities are obtained:
, the following inequalities are obtained:

Hence,  for all
for all  . This implies that
. This implies that  for all
for all  .
.
By (2.9),  is obtained. As
is obtained. As  is observed by (2.2) and that
is observed by (2.2) and that  , then
, then

is achieved. Hence,  . Finally, by (2.2) we have
. Finally, by (2.2) we have  .
.
The following theorem is a generalization of the result in [11].
Theorem 2.5.
Let  be a
be a  function on a complete CMS, where
function on a complete CMS, where  is a strongly minihedral normal cone. If
is a strongly minihedral normal cone. If  is bounded below, then there exits
is bounded below, then there exits  such that
such that

Proof.
It is enough to show that the point  , obtained in Theorem 2.4, satisfies the statement of the theorem. Following the same notation in the proof of Theorem 2.4, it is needed to show that
, obtained in Theorem 2.4, satisfies the statement of the theorem. Following the same notation in the proof of Theorem 2.4, it is needed to show that  for
for  . Assume the contrary that for some
. Assume the contrary that for some  , we have
, we have  . Then,
. Then,  implies
implies  . By triangular inequality,
. By triangular inequality,

which implies that  and thus
and thus  for all
for all  . Taking the limit when
. Taking the limit when  tends to infinity, one can obtain
tends to infinity, one can obtain  , which is in contradiction with
, which is in contradiction with  . Thus, for any
. Thus, for any  ,
,  implies
implies  , that is,
, that is,

Let  be defined by
be defined by  .
.
Theorem 2.6.
Let  be a sequentially complete QCMS and let
be a sequentially complete QCMS and let  be a strongly minihedral normal cone. Assume that for each
be a strongly minihedral normal cone. Assume that for each  , the function
, the function  defined above is continuous on
defined above is continuous on  and
and  is a family of mappings
is a family of mappings  . If there exists a l.s.c function
. If there exists a l.s.c function  such that
such that

then for each  there is a common fixed point
there is a common fixed point  of
of  such that
such that

Proof.
Let  be strongly minihedral normal cone with normal constant
be strongly minihedral normal cone with normal constant  . First note that strong minihedrality of
. First note that strong minihedrality of  guarantees that
guarantees that  exists. Let
exists. Let  and
and  for all
for all  . Note that
. Note that  , so
, so  and also
and also  .
.
For  , set
, set  and construct a sequence
and construct a sequence  as in the proof of Theorem 2.4:
as in the proof of Theorem 2.4:  such that
such that  ,
,  . Thus, one can observe that for each
. Thus, one can observe that for each  ,
,
(i) ,
,
(ii) .
.
Similar to the proof of Theorem 2.4, (ii) implies that

Also, by using the same method in the proof of Theorem 2.4, it can be shown that  is a Cauchy sequence and converges to some
is a Cauchy sequence and converges to some  and
and  .
.
We shall show that  for all
for all  . Assume the contrary that there is
. Assume the contrary that there is  such that
such that  . Then (2.16) with
. Then (2.16) with  implies that
implies that  Thus, by definition of
Thus, by definition of  , there is
, there is  such that
such that  . Since
. Since  ,
,

which implies that  . Hence
. Hence  which is in a contradiction with
which is in a contradiction with  Thus,
Thus,  for all
for all  . Since
. Since  , we have
, we have

is obtained.
The following theorem is a generalization of [13, Theorem  ].
].
Theorem 2.7.
Let  be a set,
be a set,  as in Theorem 2.6,
as in Theorem 2.6,  a surjective mapping, and
a surjective mapping, and  a family of arbitrary mappings
a family of arbitrary mappings  . If there exists a
. If there exists a  function
function  such that
such that

and each  , then
, then  and
and  have a common coincidence point, that is, for some
have a common coincidence point, that is, for some  ,
,  for all
for all  .
.
Proof.
Let  be arbitrary and
be arbitrary and  as in Theorem 2.6. Since
as in Theorem 2.6. Since  is surjective, for each
is surjective, for each  there is some
there is some  such that
such that  . Let
. Let  be a fixed mapping. Define by
be a fixed mapping. Define by  a mapping
a mapping  of
of  into itself such that
into itself such that  , where
, where  , that is,
, that is,  . Let
. Let  be a family of all mappings
be a family of all mappings  . Then, (2.21) yields that
. Then, (2.21) yields that

Thus, by Theorem 2.6,  for all
for all  . Hence
. Hence  for all
for all  , where
, where  is such that
is such that  .
.
References
Huang L-G, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. Journal of Mathematical Analysis and Applications 2007,332(2):1468–1476. 10.1016/j.jmaa.2005.03.087
Rezapour Sh, Hamlbarani R: Some notes on the paper: "cone metric spaces and fixed point theorems of contractive mappings". Journal of Mathematical Analysis and Applications 2008,345(2):719–724. 10.1016/j.jmaa.2008.04.049
Turkoglu D, Abuloha M: Cone metric spaces and fixed point theorems in diametrically contractive mappings. Acta Mathematica Sinica, English Series, submitted
Turkoglu D, Abuloha M, Abdeljawad T: KKM mappings in cone metric spaces and some fixed point theorems. Nonlinear Analysis: Theory, Methods and Applications 2010,72(1):348–353. 10.1016/j.na.2009.06.058
Şahin İ, Telci M: Fixed points of contractive mappings on complete cone metric spaces. Hacettepe Journal of Mathematics and Statistics 2008, 345: 719–724.
Rezapour Sh, Derafshpour M, Hamlbarani R: A Review on Topological Properties of Cone Metric Spaces. Analysis, Topology and Applications 2008 (ATA2008), the 30th of May to the 4th of June, 2008, Technical Faculty, Cacak, University of Kragujevac Vrnjacka Banja, Serbia
Haghi RH, Rezapour Sh: Fixed points of multifunctions on regular cone metric spaces. Expositiones Mathematicae. In press
Rezapour Sh, Haghi RH: Fixed point of multifunctions on cone metric spaces. Numerical Functional Analysis and Optimization 2009,30(7–8):825–832. 10.1080/01630560903123346
Klim D, Wardowski D: Dynamic processes and fixed points of set-valued nonlinear contractions in cone metric spaces. Nonlinear Analysis: Theory, Methods and Applications 2009,71(11):5170–5175. 10.1016/j.na.2009.04.001
Caristi J: Fixed point theorems for mappings satisfying inwardness conditions. Transactions of the American Mathematical Society 1976, 215: 241–251.
Ekeland I: Sur les problèmes variationnels. Comptes Rendus de l'Académie des Sciences 1972, 275: A1057-A1059.
Deimling K: Nonlinear Functional Analysis. Springer, Berlin, Germany; 1985:xiv+450.
Ćirić LB: On a common fixed point theorem of a Greguš type. Publications de l' Institut Mathématique 1991,49(63):174–178.
Acknowledgment
This work is partially supported by the Scientific and Technical Research Council of Turkey.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Abdeljawad, T., Karapinar, E. Quasicone Metric Spaces and Generalizations of Caristi Kirk's Theorem. Fixed Point Theory Appl 2009, 574387 (2009). https://doi.org/10.1155/2009/574387
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/574387
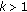 , there is a normal cone with normal constant
, there is a normal cone with normal constant 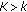 .
.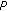 is regular if every decreasing sequence which is bounded from below is convergent.
is regular if every decreasing sequence which is bounded from below is convergent.