- Research Article
- Open access
- Published:
An Extragradient Method for Mixed Equilibrium Problems and Fixed Point Problems
Fixed Point Theory and Applications volume 2009, Article number: 632819 (2009)
Abstract
The purpose of this paper is to investigate the problem of approximating a common element of the set of fixed points of a demicontractive mapping and the set of solutions of a mixed equilibrium problem. First, we propose an extragradient method for solving the mixed equilibrium problems and the fixed point problems. Subsequently, we prove the strong convergence of the proposed algorithm under some mild assumptions.
1. Introduction
Let  be a real Hilbert space and let
be a real Hilbert space and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a real-valued function and
be a real-valued function and  be an equilibrium bifunction, that is,
be an equilibrium bifunction, that is,  for each
for each  . We consider the following mixed equilibrium problem (MEP) which is to find
. We consider the following mixed equilibrium problem (MEP) which is to find  such that
such that

In particular, if  , this problem reduces to the equilibrium problem (EP), which is to find
, this problem reduces to the equilibrium problem (EP), which is to find  such that
such that

Denote the set of solutions of (MEP) by  and the set of solutions of (EP) by
and the set of solutions of (EP) by  . The mixed equilibrium problems include fixed point problems, optimization problems, variational inequality problems, Nash equilibrium problems, and the equilibrium problems as special cases; see, for example, [1–5]. Some methods have been proposed to solve the equilibrium problems, see, for example, [5–21].
. The mixed equilibrium problems include fixed point problems, optimization problems, variational inequality problems, Nash equilibrium problems, and the equilibrium problems as special cases; see, for example, [1–5]. Some methods have been proposed to solve the equilibrium problems, see, for example, [5–21].
In 1997, Flåm and Antipin [15] introduced an iterative algorithm of finding the best approximation to the initial data when  and proved a strong convergence theorem. Recently by using the viscosity approximation method S. Takahashi and W. Takahashi [8] introduced another iterative algorithm for finding a common element of the set of solutions of (EP) and the set of fixed points of a nonexpansive mapping in a real Hilbert space. Let
and proved a strong convergence theorem. Recently by using the viscosity approximation method S. Takahashi and W. Takahashi [8] introduced another iterative algorithm for finding a common element of the set of solutions of (EP) and the set of fixed points of a nonexpansive mapping in a real Hilbert space. Let  be a nonexpansive mapping and
be a nonexpansive mapping and  be a contraction. Starting with arbitrary initial
be a contraction. Starting with arbitrary initial  , define the sequences
, define the sequences  and
and  recursively by
recursively by

-
S.
Takahashi and W. Takahashi proved that the sequences
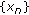 and
and 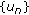 defined by (TT) converge strongly to
defined by (TT) converge strongly to  with the following restrictions on algorithm parameters
with the following restrictions on algorithm parameters 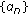 and
and 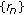 :
:
(i) and
and  ;
;
(ii) ;
;
(iii)(A1):  ; and (R1):
; and (R1):  .
.
Subsequently, some iterative algorithms for equilibrium problems and fixed point problems have further developed by some authors. In particular, Zeng and Yao [16] introduced a new hybrid iterative algorithm for mixed equilibrium problems and fixed point problems and Mainge and Moudafi [22] introduced an iterative algorithm for equilibrium problems and fixed point problems.
On the other hand, for solving the equilibrium problem (EP), Moudafi [23] presented a new iterative algorithm and proved a weak convergence theorem. Ceng et al. [24] introduced another iterative algorithm for finding an element of  . Let
. Let  be a
be a  -strict pseudocontraction for some
-strict pseudocontraction for some  such that
such that  . For given
. For given  , let the sequences
, let the sequences  and
and  be generated iteratively by
be generated iteratively by

where the parameters  and
and  satisfy the following conditions:
satisfy the following conditions:
(i) for some
for some  ;
;
(ii) and
and  .
.
Then, the sequences  and
and  generated by (CAY) converge weakly to an element of
generated by (CAY) converge weakly to an element of  .
.
At this point, we should point out that all of the above results are interesting and valuable. At the same time, these results also bring us the following conjectures.
Questions
(1)Could we weaken or remove the control condition (iii) on algorithm parameters in S. Takahashi and W. Takahashi [8]?
(2)Could we construct an iterative algorithm for  -strict pseudocontractions such that the strong convergence of the presented algorithm is guaranteed?
-strict pseudocontractions such that the strong convergence of the presented algorithm is guaranteed?
(3)Could we give some proof methods which are different from those in [8, 12, 16, 24].
It is our purpose in this paper that we introduce a general iterative algorithm for approximating a common element of the set of fixed points of a demicontractive mapping and the set of solutions of a mixed equilibrium problem. Subsequently, we prove the strong convergence of the proposed algorithm under some mild assumptions. Our results give positive answers to the above questions.
2. Preliminaries
Let  be a real Hilbert space with inner product
be a real Hilbert space with inner product  and norm
and norm  . Let
. Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  .
.
Let  be a mapping. We use
be a mapping. We use  to denote the set of the fixed points of
to denote the set of the fixed points of  . Recall what follows.
. Recall what follows.
(i) is called demicontractive if there exists a constant
is called demicontractive if there exists a constant  such that
such that

for all  and
and  , which is equivalent to
, which is equivalent to

For such case, we also say that  is a
is a  -demicontractive mapping.
-demicontractive mapping.
(ii) is called nonexpansive if
is called nonexpansive if

for all  .
.
(iii) is called quasi-nonexpansive if
is called quasi-nonexpansive if

for all  and
and  .
.
(iv) is called strictly pseudocontractive if there exists a constant
is called strictly pseudocontractive if there exists a constant  such that
such that

for all  .
.
It is worth noting that the class of demicontractive mappings includes the class of the nonexpansive mappings, the quasi-nonexpansive mappings and the strictly pseudo-contractive mappings as special cases.
Let us also recall that  is called demiclosed if for any sequence
is called demiclosed if for any sequence  and
and  , we have
, we have

It is well-known that the nonexpansive mappings, strictly pseudo-contractive mappings are all demiclosed. See, for example, [25–27].
An operator  is said to be
is said to be  -strongly monotone if there exists a positive constant
-strongly monotone if there exists a positive constant  such that
such that

for all  .
.
Now we concern the following problem: find  such that
such that

In this paper, for solving problem (2.8) with an equilibrium bifunction  , we assume that
, we assume that  satisfies the following conditions:
satisfies the following conditions:
(H1) is monotone, that is,
is monotone, that is,  for all
for all  ;
;
(H2) for each fixed  ,
,  is concave and upper semicontinuous;
is concave and upper semicontinuous;
(H3) for each  ,
,  is convex.
is convex.
A mapping  is called Lipschitz continuous, if there exists a constant
is called Lipschitz continuous, if there exists a constant  such that
such that

A differentiable function  on a convex set
on a convex set  is called
is called
(i) -convex if
-convex if

where  is the Frechet derivative of
is the Frechet derivative of  at
at  ;
;
(ii) -strongly convex if there exists a constant
-strongly convex if there exists a constant  such that
such that

Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  ,
,  be real-valued function and
be real-valued function and  be an equilibrium bifunction. Let
be an equilibrium bifunction. Let  be a positive number. For a given point
be a positive number. For a given point  , the auxiliary problem for (MEP) consists of finding
, the auxiliary problem for (MEP) consists of finding  such that
such that

Let  be the mapping such that for each
be the mapping such that for each  ,
,  is the solution set of the auxiliary problem, that is,
is the solution set of the auxiliary problem, that is,  ,
,

We need the following important and interesting result for proving our main results.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  and let
and let  be a lower semicontinuous and convex functional. Let
be a lower semicontinuous and convex functional. Let  be an equilibrium bifunction satisfying conditions (H1)–(H3). Assume what follows.
be an equilibrium bifunction satisfying conditions (H1)–(H3). Assume what follows.
(i) is Lipschitz continuous with constant
is Lipschitz continuous with constant  such that
such that
(a) ,
,
(b) is affine in the first variable,
is affine in the first variable,
(c)for each fixed  is sequentially continuous from the weak topology to the weak topology.
is sequentially continuous from the weak topology to the weak topology.
(ii) is
is  -strongly convex with constant
-strongly convex with constant  and its derivative
and its derivative  is sequentially continuous from the weak topology to the strong topology.
is sequentially continuous from the weak topology to the strong topology.
(iii)For each  , there exist a bounded subset
, there exist a bounded subset  and
and  such that for any
such that for any  ,
,

Then there hold the following:
(i) is single-valued;
is single-valued;
(ii) is nonexpansive if
is nonexpansive if  is Lipschitz continuous with constant
is Lipschitz continuous with constant  such that
such that  and
and

where  for
for  ;
;
(iii) ;
;
(iv) is closed and convex.
is closed and convex.
3. Main Results
Let  be a real Hilbert space,
be a real Hilbert space,  be a lower semicontinuous and convex real-valued function,
be a lower semicontinuous and convex real-valued function,  be an equilibrium bifunction. Let
be an equilibrium bifunction. Let  be a mapping and
be a mapping and  be a mapping. In this section, we first introduce the following new iterative algorithm.
be a mapping. In this section, we first introduce the following new iterative algorithm.
Algorithm 3.1.
Let  be a positive parameter. Let
be a positive parameter. Let  be a sequence in
be a sequence in  and
and  be a sequence in
be a sequence in  . Define the sequences
. Define the sequences  ,
,  and
and  by the following manner:
by the following manner:

Now we give a strong convergence result concerning Algorithm 3.1 as follows.
Theorem 3.2.
Let  be a real Hilbert space. Let
be a real Hilbert space. Let  be a lower semicontinuous and convex functional. Let
be a lower semicontinuous and convex functional. Let  be an equilibrium bifunction satisfying conditions (H1)–(H3). Let
be an equilibrium bifunction satisfying conditions (H1)–(H3). Let  be an
be an  -Lipschitz continuous and
-Lipschitz continuous and  -strongly monotone mapping and
-strongly monotone mapping and  be a demiclosed and
be a demiclosed and  -demicontractive mapping such that
-demicontractive mapping such that  . Assume what follows.
. Assume what follows.
(i) is Lipschitz continuous with constant
is Lipschitz continuous with constant  such that
such that
(a) ,
,
(b) is affine in the first variable,
is affine in the first variable,
(c)for each fixed  ,
,  is sequentially continuous from the weak topology to the weak topology.
is sequentially continuous from the weak topology to the weak topology.
(ii) is
is  -strongly convex with constant
-strongly convex with constant  and its derivative
and its derivative  is not only sequentially continuous from the weak topology to the strong topology but also Lipschitz continuous with constant
is not only sequentially continuous from the weak topology to the strong topology but also Lipschitz continuous with constant  such that
such that  .
.
(iii)For each  ; there exist a bounded subset
; there exist a bounded subset  and
and  such that, for any
such that, for any  ,
,

(iv) for some
for some  ,
,  and
and  .
.
Then the sequences  ,
,  , and
, and  generated by (3.1) converge strongly to
generated by (3.1) converge strongly to  which solves the problem (2.8) provided
which solves the problem (2.8) provided  is firmly nonexpansive.
is firmly nonexpansive.
Proof.
First, we prove that  ,
,  , and
, and  are all bounded. Without loss of generality, we may assume that
are all bounded. Without loss of generality, we may assume that  . Given
. Given  and
and  , we have
, we have

that is,

Take  . From (3.1), we have
. From (3.1), we have

Therefore,

where  .
.
Note that  and
and  are firmly nonexpansive. Hence, we have
are firmly nonexpansive. Hence, we have

which implies that

From (2.2) and (3.1), we have

From (3.6)–(3.9), we have

This implies that  is bounded, so are
is bounded, so are  and
and  .
.
From (3.1), we can write  . Thus, from (3.9), we have
. Thus, from (3.9), we have

Since  ,
,  . Therefore, from (3.8) and (3.11), we obtain
. Therefore, from (3.8) and (3.11), we obtain

We note that  and
and  are bounded. So there exists a constant
are bounded. So there exists a constant  such that
such that

Consequently, we get

Now we divide two cases to prove that  converges strongly to
converges strongly to  .
.
Case 1.
Assume that the sequence  is a monotone sequence. Then
is a monotone sequence. Then  is convergent. Setting
is convergent. Setting  .
.
(i)If  , then the desired conclusion is obtained.
, then the desired conclusion is obtained.
(ii)Assume that  . Clearly, we have
. Clearly, we have

this together with  and (3.14) implies that
and (3.14) implies that

that is to say

Let  be a weak limit point of
be a weak limit point of  . Then there exists a subsequence of
. Then there exists a subsequence of  , still denoted by
, still denoted by  which weakly converges to
which weakly converges to  . Noting that
. Noting that  , we also have
, we also have

Combining (3.1) and (3.17), we have

Since  is demiclosed, then we obtain
is demiclosed, then we obtain  .
.
Next we show that  . Since
. Since  , we derive
, we derive

From the monotonicity of  , we have
, we have

and hence

Since  and
and  weakly, from the weak lower semicontinuity of
weakly, from the weak lower semicontinuity of  and
and  in the second variable
in the second variable  , we have
, we have

for all  . For
. For  and
and  , let
, let  . Since
. Since  and
and  , we have
, we have  and hence
and hence  . From the convexity of equilibrium bifunction
. From the convexity of equilibrium bifunction  in the second variable
in the second variable  , we have
, we have

and hence  . Then, we have
. Then, we have

for all  and hence
and hence  .
.
Therefore, we have

Thus, if  is a solution of problem (2.8), we have
is a solution of problem (2.8), we have

Suppose that there exists another subsequence  which weakly converges to
which weakly converges to  . It is easily checked that
. It is easily checked that  and
and

Therefor, we have

Since  is
is  -strongly monotone, we have
-strongly monotone, we have

By (3.17)–(3.30), we get

From (3.12), for  , we deduce that there exists a positive integer number
, we deduce that there exists a positive integer number  large enough, when
large enough, when  ,
,

This implies that

Since  and
and  is bounded, hence the last inequality is a contraction. Therefore,
is bounded, hence the last inequality is a contraction. Therefore,  , that is to say,
, that is to say,  .
.
Case 2.
Assume that  is not a monotone sequence. Set
is not a monotone sequence. Set  and let
and let  be a mapping for all
be a mapping for all  by
by

Clearly,  is a nondecreasing sequence such that
is a nondecreasing sequence such that  as
as  and
and  for
for  . From (3.14), we have
. From (3.14), we have

thus

Therefore,

Since  , for all
, for all  , from (3.12), we get
, from (3.12), we get

which implies that

Since  is bounded, there exists a subsequence of
is bounded, there exists a subsequence of  , still denoted by
, still denoted by  which converges weakly to
which converges weakly to  . It is easily checked that
. It is easily checked that  . Furthermore, we observe that
. Furthermore, we observe that

Hence, for all  ,
,

Therefore

which implies that

Thus,

It is immediate that

Furthermore, for  , it is easily observed that
, it is easily observed that  if
if  (i.e.,
(i.e.,  ), because
), because  for
for  . As a consequence, we obtain for all
. As a consequence, we obtain for all  ,
,

Hence  , that is,
, that is,  converges strongly to
converges strongly to  . Consequently, it easy to prove that
. Consequently, it easy to prove that  and
and  converge strongly to
converge strongly to  . This completes the proof.
. This completes the proof.
Remark 3.3.
The advantages of these results in this paper are that less restrictions on the parameters  are imposed.
are imposed.
As direct consequence of Theorem 3.2, we obtain the following.
Corollary 3.4.
Let  be a real Hilbert space. Let
be a real Hilbert space. Let  be a lower semicontinuous and convex functional. Let
be a lower semicontinuous and convex functional. Let  be an equilibrium bifunction satisfying conditions (H1)–(H3). Let
be an equilibrium bifunction satisfying conditions (H1)–(H3). Let  be an
be an  -Lipschitz continuous and
-Lipschitz continuous and  -strongly monotone mapping and
-strongly monotone mapping and  be a nonexpansive mapping such that
be a nonexpansive mapping such that  . Assume what follows.
. Assume what follows.
(i) is Lipschitz continuous with constant
is Lipschitz continuous with constant  such that;
such that;
(a) ,
,
(b) is affine in the first variable,
is affine in the first variable,
(c)for each fixed  ,
,  is sequentially continuous from the weak topology to the weak topology.
is sequentially continuous from the weak topology to the weak topology.
(ii) is
is  -strongly convex with constant
-strongly convex with constant  and its derivative
and its derivative  is not only sequentially continuous from the weak topology to the strong topology but also Lipschitz continuous with constant
is not only sequentially continuous from the weak topology to the strong topology but also Lipschitz continuous with constant  such that
such that  .
.
(iii)For each  ; there exist a bounded subset
; there exist a bounded subset  and
and  such that, for any
such that, for any  ,
,

(iv) for some
for some  ,
,  and
and  .
.
Then the sequences  ,
,  , and
, and  generated by (3.1) converge strongly to
generated by (3.1) converge strongly to  which solves the problem (2.8) provided
which solves the problem (2.8) provided  is firmly nonexpansive.
is firmly nonexpansive.
Corollary 3.5.
Let  be a real Hilbert space. Let
be a real Hilbert space. Let  be a lower semicontinuous and convex functional. Let
be a lower semicontinuous and convex functional. Let  be an equilibrium bifunction satisfying conditions (H1)–(H3). Let
be an equilibrium bifunction satisfying conditions (H1)–(H3). Let  be an
be an  -Lipschitz continuous and
-Lipschitz continuous and  -strongly monotone mapping and
-strongly monotone mapping and  be a strictly pseudo-contractive mapping such that
be a strictly pseudo-contractive mapping such that  . Assume what follows.
. Assume what follows.
(i) is Lipschitz continuous with constant
is Lipschitz continuous with constant  such that
such that
(a) ,
,
(b) is affine in the first variable,
is affine in the first variable,
(c)for each fixed  ,
,  is sequentially continuous from the weak topology to the weak topology.
is sequentially continuous from the weak topology to the weak topology.
(ii) is
is  -strongly convex with constant
-strongly convex with constant  and its derivative
and its derivative  is not only sequentially continuous from the weak topology to the strong topology but also Lipschitz continuous with constant
is not only sequentially continuous from the weak topology to the strong topology but also Lipschitz continuous with constant  such that
such that  .
.
(iii)For each  ; there exist a bounded subset
; there exist a bounded subset  and
and  such that, for any
such that, for any  ,
,

(iv) for some
for some  ,
,  and
and  .
.
Then the sequences  ,
,  and
and  generated by (3.1) converge strongly to
generated by (3.1) converge strongly to  which solves the problem (2.8) provided
which solves the problem (2.8) provided  is firmly nonexpansive.
is firmly nonexpansive.
References
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994, 63: 123–145.
Zeng L-C, Wu S-Y, Yao J-C: Generalized KKM theorem with applications to generalized minimax inequalities and generalized equilibrium problems. Taiwanese Journal of Mathematics 2006,10(6):1497–1514.
Chadli O, Wong NC, Yao J-C: Equilibrium problems with applications to eigenvalue problems. Journal of Optimization Theory and Applications 2003,117(2):245–266. 10.1023/A:1023627606067
Chadli O, Schaible S, Yao J-C: Regularized equilibrium problems with application to noncoercive hemivariational inequalities. Journal of Optimization Theory and Applications 2004,121(3):571–596.
Konnov IV, Schaible S, Yao J-C: Combined relaxation method for mixed equilibrium problems. Journal of Optimization Theory and Applications 2005,126(2):309–322. 10.1007/s10957-005-4716-0
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. Journal of Nonlinear and Convex Analysis 2005,6(1):117–136.
Flåm SD, Antipin AS: Equilibrium programming using proximal-like algorithms. Mathematical Programming 1997,78(1):29–41.
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,331(1):506–515. 10.1016/j.jmaa.2006.08.036
Chadli O, Konnov IV, Yao J-C: Descent methods for equilibrium problems in a banach space. Computers and Mathematics with Applications 2004,48(3–4):609–616. 10.1016/j.camwa.2003.05.011
Ding X-P, Lin Y-C, Yao J-C: Predictor-corrector algorithms for solving generalized mixed implicit quasi-equilibrium problems. Applied Mathematics and Mechanics 2006,27(9):1157–1164. 10.1007/s10483-006-0901-1
Yao Y, Liou Y-C, Yao J-C: Convergence theorem for equilibrium problems and fixed point problems of infinite family of nonexpansive mappings. Fixed Point Theory and Applications 2007, Article ID 64363, 2007:-12.
Plubtieng S, Punpaeng R: A general iterative method for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,336(1):455–469. 10.1016/j.jmaa.2007.02.044
Tada A, Takahashi W: Strong convergence theorem for an equilibrium problem and a nonexpansive mapping. In Nonlinear Analysis and Convex Analysis. Edited by: Takahashi W, Tanaka T. Yokohama, Yokohama, Japan; 2007:609–617.
Noor MA: Fundamentals of equilibrium problems. Mathematical Inequalities & Applications 2006,9(3):529–566.
Yao Y, Noor MA, Liou Y-C: On iterative methods for equilibrium problems. Nonlinear Analysis 2009, 70: 497–509. 10.1016/j.na.2007.12.021
Zeng L-C, Yao J-C: A hybrid iterative scheme for mixed equilibrium problems and fixed point problems. Journal of Computational and Applied Mathematics 2008,214(1):186–201. 10.1016/j.cam.2007.02.022
Yao Y, Noor MA, Zainab S, Liou Y-C: Mixed equilibrium problems and optimization problems. Journal of Mathematical Analysis and Applications 2009,354(1):319–329. 10.1016/j.jmaa.2008.12.055
Yao Y, Zhou H, Liou Y-C: Weak and strong convergence theorems for an asymptotically -strict pseudocontraction and a mixed equilibrium problem. Journal of the Korean Mathematical Society 2009, 46: 561–576. 10.4134/JKMS.2009.46.3.561
Mainge P-E: Regularized and inertial algorithms for common fixed points of nonlinear operators. Journal of Mathematical Analysis and Applications 2008,344(2):876–887. 10.1016/j.jmaa.2008.03.028
Yao Y, Liou Y-C, Yao J-C: An iterative algorithm for approximating convex minimization problem. Applied Mathematics and Computation 2007,188(1):648–656. 10.1016/j.amc.2006.10.039
Marino G, Colao V, Muglia L, Yao Y: Krasnoselski-Mann iteration for hierarchical fixed points and equilibrium problem. Bulletin of the Australian Mathematical Society 2009, 79: 187–200. 10.1017/S000497270800107X
Mainge P-E, Moudafi A: Coupling viscosity methods with the extragradient algorithm for solving equilibrium problems. Journal of Nonlinear and Convex Analysis 2008,9(2):283–294.
Moudafi A: Weak convergence theorems for nonexpansive mappings and equilibrium problems. Journal of Nonlinear and Convex Analysis 2008,9(1):37–43.
Ceng L-C, Al-Homidan S, Ansari QH, Yao J-C: An iterative scheme for equilibrium problems and fixed point problems of strict pseudo-contraction mappings. Journal of Computational and Applied Mathematics 2009,223(2):967–974. 10.1016/j.cam.2008.03.032
Marino G, Xu H-K: Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,329(1):336–346. 10.1016/j.jmaa.2006.06.055
Zeng L-C, Wong N-C, Yao J-C: Strong convergence theorems for strictly pseudocontractive mappings of Browder-Petryshyn type. Taiwanese Journal of Mathematics 2006,10(4):837–849.
Zhou H: Convergence theorems of common fixed points for a finite family of Lipschitz pseudocontractions in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,68(10):2977–2983. 10.1016/j.na.2007.02.041
Konnov IV: Generalized monotone equilibrium problems and variational inequalities. In Handbook of Generalized Convexity and Generalized Monotonicity. Edited by: Hadjisavvas N, Komlosi S, Schaible S. Springer, New York, NY, USA; 2005.
Acknowledgment
The authors are extremely grateful to the anonymous referee for his/her useful comments and suggestions. The first author was partially supposed by National Natural Science Foundation of China Grant 10771050. The second author was partially supposed by the Grant NSC 97-2221-E-230-017.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yao, Y., Liou, YC. & Wu, YJ. An Extragradient Method for Mixed Equilibrium Problems and Fixed Point Problems. Fixed Point Theory Appl 2009, 632819 (2009). https://doi.org/10.1155/2009/632819
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/632819
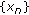 and
and 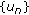 defined by (TT) converge strongly to
defined by (TT) converge strongly to  with the following restrictions on algorithm parameters
with the following restrictions on algorithm parameters 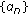 and
and 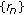 :
: