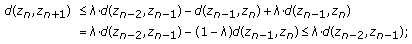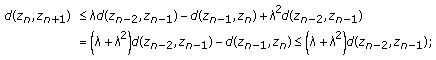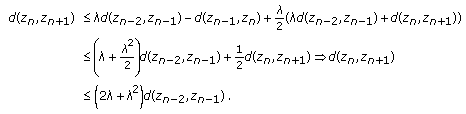- Research Article
- Open access
- Published:
Assad-Kirk-Type Fixed Point Theorems for a Pair of Nonself Mappings on Cone Metric Spaces
Fixed Point Theory and Applications volume 2009, Article number: 761086 (2009)
Abstract
New fixed point results for a pair of non-self mappings defined on a closed subset of a metrically convex cone metric space (which is not necessarily normal) are obtained. By adapting Assad-Kirk's method the existence of a unique common fixed point for a pair of non-self mappings is proved, using only the assumption that the cone interior is nonempty. Examples show that the obtained results are proper extensions of the existing ones.
1. Introduction and Preliminaries
Cone metric spaces were introduced by Huang and Zhang in [1], where they investigated the convergence in cone metric spaces, introduced the notion of their completeness, and proved some fixed point theorems for contractive mappings on these spaces. Recently, in [2–4], some common fixed point theorems have been proved for maps on cone metric spaces. However, in [1–3], the authors usually obtain their results for normal cones. In this paper we do not impose the normality condition for the cones.
We need the following definitions and results, consistent with [1], in the sequel.
Let 
be a real Banach space. A subset 
of 
is a cone if
(i)
is closed, nonempty and 
(ii)
, and 
imply 
(iii)
.
Given a cone 
, we define the partial ordering 
with respect to 
by 
if and only if 
. We write 
to indicate that 
but 
, while 
stands for 
(the interior of 
).
There exist two kinds of cones: normal and nonnormal cones. A cone 
is a normal cone if
or, equivalently, if there is a number 
such that for all 
,
The least positive number satisfying (1.2) is called the normal constant of 
. It is clear that 
.
It follows from (1.1) that 
is nonnormal if and only if there exist sequences 
such that
So, in this case, the Sandwich theorem does not hold.
Example 1.1 (see [5]).
Let 
with 
and 
. This cone is not normal. Consider, for example,
Then 
and 
.
Definition 1.2 (see [1]).
Let 
be a nonempty set. Suppose that the mapping 
satisfies
(d1)
for all 
and 
if and only if 
;
(d2)
for all 
;
(d3)
for all 
.
Then 
is called a cone metric on 
and 
is called a cone metric space.
The concept of a cone metric space is more general than that of a metric space, because each metric space is a cone metric space with 
and 
(see [1, Example??1] and [4, Examples??1.2 and??2.2]).
Let 
be a sequence in 
, and let 
. If, for every 
in 
with 
, there is an 
such that for all 
, 
, then it is said that 
converges to 
, and this is denoted by 
, or 
, 
. If for every 
in 
with 
, there is an 
such that for all 
, 
, then 
is called a Cauchy sequence in 
. If every Cauchy sequence is convergent in 
, then 
is called a complete cone metric space.
Huang and Zhang [1] proved that if 
is a normal cone then 
converges to 
if and only if 
, 
, and that 
is a Cauchy sequence if and only if 
, 
.
Let 
be a cone metric space. Then the following properties are often useful (particulary when dealing with cone metric spaces in which the cone needs not to be normal):
() if 
and 
, then 
() if 
for each 
then 
() if 
for each 
then 
() if 
, and 
, then 
() if 
for each 
and 
, 
, then 
() if 
and 
, then 
where 
and 
are, respectively, a sequence and a given point in 
() if 
is a real Banach space with a cone 
and if 
where 
and 
, then 
() if 
, 
and 
, then there exists 
such that for all 
we have 
.
It follows from (
) that the sequence 
converges to 
if 
as 
and 
is a Cauchy sequence if 
as 
. In the case when the cone is not necessarily normal, we have only one half of the statements of Lemmas??1 and??4 from [1]. Also, in this case, the fact that 
if 
and 
is not applicable.
There exist a lot of fixed-point theorems for self-mappings defined on closed subsets of Banach spaces. However, for applications (numerical analysis, optimization, etc.) it is important to consider functions that are not self-mappings, and it is natural to search for sufficient conditions which would guarantee the existence of fixed points for such mappings.
In what follows we suppose only that 
is a Banach space, that 
is a cone in 
with 
and that 
is the partial ordering with respect to 
.
Rhoades [6] proved the following result, generalizing theorems of Assad [7] and Assad and Kirk [8].
Theorem 1.3.
Let 
be a Banach space, 
a nonempty closed subset of 
and let 
be a mapping from 
into 
satisfying the condition
for some 
, 
, and for all 
in 
. Let 
have the additional property that for each 
, 
the boundary of 
, 
. Then 
has the unique fixed point.
Recently Imdad and Kumar [9] extended this result of Rhoades by considering a pair of maps in the following way.
Theorem 1.4.
Let 
be a Banach space, let 
be a nonempty closed subset of 
and let 
be two mappings satisfying the condition
for some 
, 
, and for all 
and suppose
(i)
, 
,
(ii)
,
(iii)
is closed in 
.
Then there exists a coincidence point 
of 
in 
. Moreover, if 
and 
are coincidentally commuting, then 
is the unique common fixed point of 
and 
.
Recall that a pair 
of mappings is coincidentally commuting (see, e.g., [2]) if they commute at their coincidence point, that is, if 
for some 
, implies 
.
In [10, 11] these results were extended using complete metric spaces of hyperbolic type, instead of Banach spaces.
2. Results
2.1. Main Result
In [12], assuming only that 
, Theorems 1.3 and 1.4 are extended to the setting of cone metric spaces. Thus, proper generalizations of the results of Rhoades [6] (for one map) and of Imdad and Kumar [9] (for two maps) were obtained. Example 1.1 of a nonnormal cone shows that the method of proof used in [6, 8, 9] cannot be fully applied in the new setting.
The purpose of this paper is to extend the previous results to the cone metric spaces, but with new contractive conditions. This is worthwhile, since from [2, 13] we know that self-mappings that satisfy the new conditions (given below) do have a unique common fixed point. Let us note that the questions concerning common fixed points for self-mappings in metric spaces, under similar conditions, were considered in [14]. It seems that these questions were not considered for nonself mappings. This is an additional motivation for studying these problems.
We begin with the following definition.
Definition 2.1.
Let 
be a cone metric space, let 
be a nonempty closed subset of 
, and let 
. Denote, for 
,
Then 
is called a generalized
-contractive mapping of 
into 
if for some 
there exists
such that for all 
in 
Our main result is the following.
Theorem 2.2.
Let 
be a complete cone metric space, let 
be a nonempty closed subset of 
such that, for each 
and each 
there exists a point 
such that
Suppose that 
is a generalized 
-contractive mapping of 
into 
and
(i)
, 
,
(ii)
,
(iii)
is closed in 
.
Then there exists a coincidence point 
of 
in 
. Moreover, if the pair 
is coincidentally commuting, then 
is the unique common fixed point of 
and 
.
Proof.
We prove the theorem under the hypothesis that neither of the mappings 
and 
is necessarily a self-mapping. We proceed in several steps.
Step 1 (construction of three sequences).
The following construction is the same as the construction used in [10] in the case of hyperbolic metric spaces. It differs slightly from the constructions in [6, 9].
Let 
be arbitrary. We construct three sequences: 
and 
in 
and 
in 
in the following way. Set 
. Since 
, by (i) there exists a point 
such that 
. Since 
, from (ii) we conclude that 
. Then from (i), 
. Thus, there exists 
such that 
. Set 
and 
.
If 
, then from (i), 
and so there is a point 
such that 
.
If 
, then 
is a point in 
, 
such that 
. By (i), there is 
such that 
. Thus 
and 
.
Now we set 
. Since 
, from (ii) there is a point 
such that 
.
Note that in the case 
, we have 
and 
.
Continuing the foregoing procedure we construct three sequences: 
, 
and 
such that:
(a)
;
(b)
;
(c)
if and only if 
;
(d)
whenever 
and then 
and 
.
Step 2 ( 
is a Cauchy sequence).
First, note that if 
, then 
, which then implies, by (b), (ii), and (a), that 
Also, 
implies that 
since otherwise 
, which then implies 
.
Proof of Step 2
Now we have to estimate 
. If 
for some 
, then it is easy to show that 
for all 
Suppose that 
for all 
. There are three possibilities:
(1)
and 
;
(2)
, but 
; and
(3)
in which case 
and 
.
Note that the estimate of 
in this cone version differs from those from [6, 8–11]. In the case of convex metric spaces it can be used that, for each 
and each 
, it is 
. In cone spaces the maximum of the set 
needs not to exist. Therefore, besides (2.4), we have to use here the relation "
'', and to consider several cases. In cone metric spaces as well as in metric spaces the key step is Assad-Kirk's induction.
Case 1.
Let 
and let 
. Then 
, 
and 
(observe that it is not necessarily 
). Then from (2.3),
where
Clearly, there are infinitely many 
's such that at least one of the following cases holds:
(I)
(II)
contradicting the assumption that 
for each 
. Hence, (I) holds,
(III)
, that is, (I) holds.
From (I), (II), and (III) it follows that in Case 1
Case 2.
Let 
but 
. Then 
and 
. It follows that
that is, according to (2.3), 
, where
Again, we obtain the following three cases
(I)
.
(II)
, contradicting the assumption that 
for each 
. It follows that (I) holds.
(III)
, that is 
.
From (2.8), (I), (II), and (III), we have
in Case 2.
Case 3.
Let 
Then 
and we have 
and 
. From this and using (2.4) we get
We have to estimate 
and 
. Since 
, one can conclude that
in view of Case 2. Further,
where
Since
, 
, and 
, we have that
where
Substituting (2.12) and (2.16) into (2.11) we get
We have now the following four cases:
-
(I)
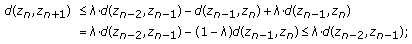(2.19)
-
(II)
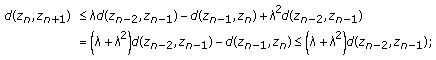(2.20)
-
(III)
(2.21)
-
(IV)
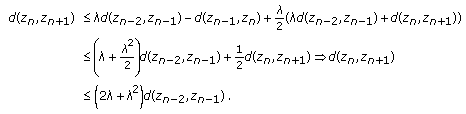(2.22)
It follows from (I), (II), (III), and (IV) that
Thus, in all Cases 1–3,
where 
and
It is not hard to conclude that for 
,
Now, following the procedure of Assad and Kirk [8], it can be shown by induction that, for 
,
where 
.
From (2.27) and using the triangle inequality, we have for 
According to the property (
) from the Introduction, 
that is, 
is a Cauchy sequence.
Step 3 (Common fixed point for 
and 
).
In this step we use only the definition of convergence in the terms of the relation "
''. The only assumption is that the interior of the cone 
is nonempty; so we use neither continuity of vector metric 
, nor the Sandwich theorem.
Since 
and 
is complete, there is some point 
such that 
. Let 
be such that 
. By the construction of 
, there is a subsequence 
such that 
and hence 
.
We now prove that 
. We have
where
From the definition of convergence and the fact that 
, as 
, we obtain (for the given 
with 
)
In all the cases we obtain 
for each 
. According to the property (
), it follows that 
, that is, 
.
Suppose now that 
and 
are coincidentally commuting. Then
Then from (2.3),
where
Hence, we obtain the following cases:
which implies that 
, that is, 
is a common fixed point of 
and 
.
Uniqueness of the common fixed point follows easily. This completes the proof of the theorem.
2.2. Examples
We present now two examples showing that Theorem 2.2 is a proper extension of the known results. In both examples, the conditions of Theorem 2.2 are fulfilled, but in the first one (because of nonnormality of the cone) the main theorems from [6, 9] cannot be applied. This shows that Theorem 2.2 is more general, that is, the main theorems from [6, 9] can be obtained as its special cases (for 
) taking 
, 
and 
.
Example 2.3 (The case of a nonnormal cone).
Let 
, let 
, and 
, and let 
. The mapping 
is defined in the following way: 
, where 
is a fixed function, for example, 
. Take functions 
, 
, 
, so that 
, which map the set 
into 
. We have that 
is a complete cone metric space with a nonnormal cone having the nonempty interior. The topological and "metric'' notions are used in the sense of definitions from [15, 16]. For example, one easily checks the condition (2.4), that is, that for 
, 
the following holds
The mappings 
and 
are weakly compatible, that is, they commute in their fixed point 
. All the conditions of Theorem 2.2 are fulfilled, and so the nonself mappings 
and 
have a unique common fixed point 
.
Example 2.4 (The case of a normal cone).
Let 
, let 
, let 
, and let 
. The mapping 
is defined as 
, 
. Take the functions 
, 
, 
, so that 
, which map the set 
into 
. We have that 
is a complete cone metric space with a normal cone having the normal coefficient 
, whose interior is obviously nonempty. All the conditions of Theorem 2.2 are fulfilled. We check again the condition (2.4), that is, that for 
, 
the following holds
The mappings 
and 
are weakly compatible, that is, they commute in their fixed point 
. All the conditions of Theorem 2.2 are again fulfilled. The point 
is the unique common fixed point for nonself mappings 
and 
.
2.3. Further Results
Remark 2.5.
The following definition is a special case of Definition 2.1 when 
is a metric space. But when 
is a cone metric space, which is not a metric space, this is not true. Indeed, there may exist 
such that the vectors 
and 
are incomparable. For the same reason Theorems 2.2 and 2.7 (given below) are incomparable.
Definition 2.6.
Let 
be a cone metric space, let 
be a nonempty closed subset of 
, and let 
. Denote
Then 
is called a generalized
-contractive mapping from 
into 
if for some 
there exists
such that for all 
in 
Our next result is the following.
Theorem 2.7.
Let 
be a complete cone metric space, and let 
be a nonempty closed subset of 
such that for each 
and 
there exists a point 
such that
Suppose that 
is a generalized 
-contractive mapping of 
into 
and
(i)
, 
,
(ii)
,
(iii)
is closed in 
.
Then there exists a coincidence point 
of 
and 
in 
. Moreover, if the pair 
is coincidentally commuting, then 
is the unique common fixed point of 
and 
.
The proof of this theorem is very similar to the proof of Theorem 2.2 and it is omitted.
We now list some corollaries of Theorems 2.2 and 2.7.
Corollary 2.8.
Let 
be a complete cone metric space, and let 
be a nonempty closed subset of 
such that, for each 
and each 
there exists a point 
such that
Let 
be such that
for some 
and for all 
.
Suppose, further, that 
and 
satisfy the following conditions:
(i)
, 
,
(ii)
,
(iii)
is closed in 
.
Then there exists a coincidence point 
of 
and 
in 
. Moreover, if 
is a coincidentally commuting pair, then 
is the unique common fixed point of 
and 
.
Corollary 2.9.
Let 
be a complete cone metric space, and let 
be a nonempty closed subset of 
such that, for each 
and each 
there exists a point 
such that
Let 
be such that
for some 
and for all 
.
Suppose, further, that 
and 
satisfy the following conditions:
(i)
, 
,
(ii)
,
(iii)
is closed in 
.
Then there exists a coincidence point 
of 
and 
in 
. Moreover, if 
is a coincidentally commuting pair, then 
is the unique common fixed point of 
and 
.
Corollary 2.10.
Let 
be a complete cone metric space, and let 
be a nonempty closed subset of 
such that, for each 
and each 
there exists a point 
such that
Let 
be such that
for some 
and for all 
.
Suppose, further, that 
and 
satisfy the following conditions:
(i)
, 
,
(ii)
,
(iii)
is closed in 
.
Then there exists a coincidence point 
of 
and 
in 
. Moreover, if 
is a coincidentally commuting pair, then 
is the unique common fixed point of 
and 
.
Remark 2.11.
Corollaries 2.8–2.10 are the corresponding theorems of Abbas and Jungck from [2] in the case that 
are nonself mappings.
Remark 2.12.
If 
is a metrically convex cone metric space, that is, if for each 
there is 
such that 
, we do not know whether (2.4) holds for every nonempty closed subset 
in 
(see [8]).
References
Huang L-G, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. Journal of Mathematical Analysis and Applications 2007,332(2):1468–1476. 10.1016/j.jmaa.2005.03.087
Abbas M, Jungck G: Common fixed point results for noncommuting mappings without continuity in cone metric spaces. Journal of Mathematical Analysis and Applications 2008,341(1):416–420. 10.1016/j.jmaa.2007.09.070
Ilic D, Rakocevic V: Common fixed points for maps on cone metric space. Journal of Mathematical Analysis and Applications 2008,341(2):876–882. 10.1016/j.jmaa.2007.10.065
Rezapour Sh, Hamlbarani R: Some notes on the paper: "Cone metric spaces and fixed point theorems of contractive mappings". Journal of Mathematical Analysis and Applications 2008,345(2):719–724. 10.1016/j.jmaa.2008.04.049
Deimling K: Nonlinear Functional Analysis. Springer, Berlin, Germany; 1985:xiv+450.
Rhoades BE: A fixed point theorem for some non-self-mappings. Mathematica Japonica 1978,23(4):457–459.
Assad NA: On a fixed point theorem of Kannan in Banach spaces. Tamkang Journal of Mathematics 1976,7(1):91–94.
Assad NA, Kirk WA: Fixed point theorems for set-valued mappings of contractive type. Pacific Journal of Mathematics 1972,43(3):553–562.
Imdad M, Kumar S: Rhoades-type fixed-point theorems for a pair of nonself mappings. Computers & Mathematics with Applications 2003,46(5–6):919–927. 10.1016/S0898-1221(03)90153-2
Ciric Lj: Non-self mappings satisfying non-linear contractive condition with applications. Nonlinear Analysis, Theory, Methods and Applications 2009,71(7–8):2927–2935. 10.1016/j.na.2009.01.174
Gajic Lj, Rakocevic V: Pair of non-self-mappings and common fixed points. Applied Mathematics and Computation 2007,187(2):999–1006. 10.1016/j.amc.2006.09.143
Radenovic S, Rhoades BE: Fixed point theorem for two non-self mappings in cone metric spaces. Computers and Mathematics with Applications 2009,57(10):1701–1707. 10.1016/j.camwa.2009.03.058
Jungck G, Radenovic S, Radojevic S, Rakocevic V: Common fixed point theorems for weakly compatible pairs on cone metric spaces. Fixed Point Theory and Applications 2009, 2009: 13.
Rhoades BE: A comparison of various definitions of contractive mappings. Transactions of the American Mathematical Society 1977, 226: 257–290.
Kadelburg Z, Radenovic S, Rakocvic V: Remarks on "Quasi-contractions on cone metric spaces". Applied Mathematics Letters, (2009). In press
Rezapour Sh: A review on topological properties of cone metric spaces. Proceedings of the International Conference Analysis, Topology and Applications (ATA '08), May-June 2008, Vrnjacka Banja, Serbia
Acknowledgment
This work was supported by Grant 14021 of the Ministry of Science and Environmental Protection of Serbia.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jankovic, S., Kadelburg, Z., Radenovic, S. et al. Assad-Kirk-Type Fixed Point Theorems for a Pair of Nonself Mappings on Cone Metric Spaces. Fixed Point Theory Appl 2009, 761086 (2009). https://doi.org/10.1155/2009/761086
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/761086