- Research Article
- Open access
- Published:
Global Attractivity Results for Mixed-Monotone Mappings in Partially Ordered Complete Metric Spaces
Fixed Point Theory and Applications volume 2009, Article number: 762478 (2009)
Abstract
We prove fixed point theorems for mixed-monotone mappings in partially ordered complete metric spaces which satisfy a weaker contraction condition than the classical Banach contraction condition for all points that are related by given ordering. We also give a global attractivity result for all solutions of the difference equation  ,
,  where
where  satisfies mixed-monotone conditions with respect to the given ordering.
satisfies mixed-monotone conditions with respect to the given ordering.
1. Introduction and Preliminaries
The following results were obtained first in [1] and were extended to the case of higher-order difference equations and systems in [2–6]. For the sake of completeness and the readers convenience, we are including short proofs.
Theorem 1.1.
Let  be a compact interval of real numbers, and assume that
be a compact interval of real numbers, and assume that

is a continuous function satisfying the following properties:
-
(a)
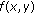 is nondecreasing in
is nondecreasing in  for each
for each  , and
, and 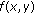 is nonincreasing in
is nonincreasing in  for each
for each 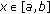 ;
; -
(b)
If
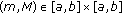 is a solution of the system
is a solution of the system  (1.2)
(1.2)
then  .
.
Then

has a unique equilibrium  and every solution of (1.3) converges to
and every solution of (1.3) converges to  .
.
Proof.
Set

and for  set
set

Now observe that for each  ,
,

Set

Then

and by the continuity of  ,
,

Therefore in view of (b),

from which the result follows.
Theorem 1.2.
Let  be an interval of real numbers and assume that
be an interval of real numbers and assume that

is a continuous function satisfying the following properties:
(a) is nonincreasing in
is nonincreasing in  for each
for each  , and
, and  is nondecreasing in
is nondecreasing in  for each
for each  ;
;
(b)the difference equation (1.3) has no solutions of minimal period two in  . Then (1.3) has a unique equilibrium
. Then (1.3) has a unique equilibrium  and every solution of (1.3) converges to
and every solution of (1.3) converges to  .
.
Proof.
Set

and for  set
set

Now observe that for each  ,
,

Set

Then clearly (1.8) holds and by the continuity of  ,
,

In view of (b),

from which the result follows.
These results have been very useful in proving attractivity results for equilibrium or periodic solutions of (1.3) as well as for higher-order difference equations and systems of difference equations; see [2, 7–12]. Theorems 1.1 and 1.2 have attracted considerable attention of the leading specialists in difference equations and discrete dynamical systems and have been generalized and extended to the case of maps in  , see [3], and maps in Banach space with the cone see [4–6]. In this paper, we will extend Theorems 1.1 and 1.2 to the case of monotone mappings in partially ordered complete metric spaces.
, see [3], and maps in Banach space with the cone see [4–6]. In this paper, we will extend Theorems 1.1 and 1.2 to the case of monotone mappings in partially ordered complete metric spaces.
On the other hand, there has been recent interest in establishing fixed point theorems in partially ordered complete metric spaces with a contractivity condition which holds for all points that are related by partial ordering; see [13–20]. These fixed point results have been applied mainly to the existence of solutions of boundary value problems for differential equations and one of them, namely [20], has been applied to the problem of solving matrix equations. See also [21], where the application to the boundary value problems for integro-differential equations is given and [22] for application to some classes of nonexpansive mappings and [23] for the application of the Leray-Schauder theory to the problems of an impulsive boundary value problem under the condition of non-well-ordered upper and lower solutions. None of these results is global result, but they are rather existence results. In this paper, we combine the existence results with the results of the type of Theorems 1.1 and 1.2 to obtain global attractivity results.
2. Main Results: Mixed Monotone Case I
Let  be a partially ordered set and let
be a partially ordered set and let  be a metric on
be a metric on  such that
such that  is a complete metric space. Consider
is a complete metric space. Consider  We will use the following partial ordering.
We will use the following partial ordering.
For  , we have
, we have

This partial ordering is well known as "south-east ordering" in competitive systems in the plane; see [5, 6, 12, 24, 25].
Let  be a metric on
be a metric on  defined as follows:
defined as follows:

Clearly

We prove the following theorem.
Theorem 2.1.
Let  be a map such that
be a map such that  is nonincreasing in
is nonincreasing in  for all
for all  and nondecreasing in
and nondecreasing in  for all
for all  Suppose that the following conditions hold.
Suppose that the following conditions hold.
(i)There exists  with
with

-
(ii)
There exists
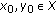 such that the following condition holds:
such that the following condition holds:  (2.5)
(2.5)
-
(iii)
If
 is a nondecreasing convergent sequence such that
is a nondecreasing convergent sequence such that 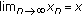 , then
, then 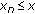 , for all
, for all 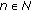 and if
and if  is a nonincreasing convergent sequence such that
is a nonincreasing convergent sequence such that  , then
, then 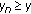 , for all
, for all 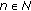 ; if
; if 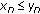 for every
for every  , then
, then 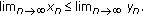
Then we have the following.
-
(a)
For every initial point
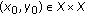 such that condition (2.5) holds,
such that condition (2.5) holds,  , where
, where 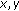 satisfy
satisfy  (2.6)
(2.6)
If  in condition (2.5), then
in condition (2.5), then  If in addition
If in addition  , then
, then  converge to the equilibrium of the equation
converge to the equilibrium of the equation

-
(b)
In particular, every solution
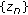 of
of  (2.8)
(2.8)
such that  converges to the equilibrium of (2.8).
converges to the equilibrium of (2.8).
-
(c)
The following estimates hold:
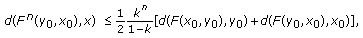 (2.9)
(2.9)

Proof.
Let  and
and  Since
Since  and
and  for
for  we have
we have

Now, we have

For  we let
we let

By using the monotonicity of  , we obtain
, we obtain

that is

We claim that for all  the following inequalities hold:
the following inequalities hold:


Indeed, for  using
using  ,??
,?? , and (2.3), we obtain
, and (2.3), we obtain

Assume that (2.16) holds. Using the inequalities

and the contraction condition (2.4), we have

Similarly,

This implies that  and
and  are Cauchy sequences in
are Cauchy sequences in 
Indeed,

Since  we have
we have

Using (2.23), we conclude that  is a Cauchy sequence. Similarly, we conclude that
is a Cauchy sequence. Similarly, we conclude that  is a Cauchy sequence. Since
is a Cauchy sequence. Since  is a complete metric space, then there exist
is a complete metric space, then there exist  such that
such that

Using the continuity of  which follows from contraction condition (2.4), the equations
which follows from contraction condition (2.4), the equations

imply (2.6).
Assume that  Then, in view of the monotonicity of
Then, in view of the monotonicity of 

By using induction, we can show that  for all
for all  Assume that
Assume that  Then, in view of the monotonicity of
Then, in view of the monotonicity of  , we have
, we have

Continuing in a similar way we can prove that  for all
for all  By using condition (iii) we conclude that whenever
By using condition (iii) we conclude that whenever  exists we must have
exists we must have

which in the case when  implies
implies 
By letting  in (2.23), we obtain the estimate (2.9).
in (2.23), we obtain the estimate (2.9).
Remark 2.2.
Property (iii) is usually called closedness of the partial ordering, see [6], and is an important ingredient of the definition of an ordered  -space; see [17, 19].
-space; see [17, 19].
Theorem 2.3.
Assume that along with conditions (i) and (ii) of Theorem 2.1, the following condition is satisfied:
-
(iv)
every pair of elements has either a lower or an upper bound.
Then, the fixed point  is unique and
is unique and 
Proof.
First, we prove that the fixed point  is unique. Condition (iv) is equivalent to the following. For every
is unique. Condition (iv) is equivalent to the following. For every  there exists
there exists  that is comparable to
that is comparable to  See [16].
See [16].
Let  and
and  be two fixed points of the map
be two fixed points of the map  .
.
We consider two cases.
Case 1.
If  is comparable to
is comparable to  then for all
then for all  is comparable to
is comparable to  We have to prove that
We have to prove that

Indeed, using (2.2), we obtain

We estimate  , and
, and 
First, by using contraction condition (2.4), we have

Now, by using (2.31) and (2.30), we have

which implies that

Case 2.
If  is not comparable to
is not comparable to  then there exists an upper bound or a lower bound
then there exists an upper bound or a lower bound  of
of  and
and  Then,
Then,  is comparable to
is comparable to  and
and 
Therefore, we have

Now, we obtain

We now estimate the right-hand side of (2.35).
First, by using

we have

Similarly,

So,

Using induction, we obtain

Using (2.40), relation (2.35) becomes

So,

Finally, we prove that  We will consider two cases.
We will consider two cases.
Case A.
If  is comparable to
is comparable to  then
then  is comparable to
is comparable to  Now, we obtain
Now, we obtain

since  this implies
this implies

Case B.
If  is not comparable to
is not comparable to  then there exists an upper bound or alower bound of
then there exists an upper bound or alower bound of  and
and  , that is, there exists
, that is, there exists  such that
such that  Then by using monotonicity character of
Then by using monotonicity character of  we have
we have

Now,

that is

Furthermore,

that is

Similarly,

that is

and

By using induction, we have

Since  is a fixed point, we obtain
is a fixed point, we obtain

Using the contractivity condition (2.4) on  we have
we have

Now, we estimate the terms on the right-hand side

Now, we have

Continuing this process, we obtain

Using the contractivity of  we have
we have

That is

So,

3. Main Results: Mixed Monotone Case II
Let  be a partially ordered set and let
be a partially ordered set and let  be a metric on
be a metric on  such that
such that  is a complete metric space. Consider
is a complete metric space. Consider  We will use the following partial order.
We will use the following partial order.
For  , we have
, we have

Let  be a metric on
be a metric on  defined as follows:
defined as follows:

The following two theorems have similar proofs to the proofs of Theorems 2.1 and 2.3, respectively, and so their proofs will be skipped. Significant parts of these results have been included in [14] and applied successfully to some boundary value problems in ordinary differential equations.
Theorem 3.1.
Let  be a map such that
be a map such that  is nondecreasing in
is nondecreasing in  for all
for all  and nonincreasing in
and nonincreasing in  for all
for all  Suppose that the following conditions hold.
Suppose that the following conditions hold.
-
(i)
There exists
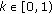 with
with 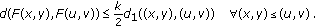 (3.3)
(3.3)
-
(ii)
There exists
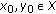 such that the following condition holds:
such that the following condition holds:  (3.4)
(3.4)
-
(iii)
If
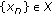 is a nondecreasing convergent sequence such that
is a nondecreasing convergent sequence such that  , then
, then  , for all
, for all 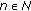 and if
and if 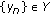 is a nonincreasing convergent sequence such that
is a nonincreasing convergent sequence such that  , then
, then  , for all
, for all  ; if
; if 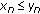 for every
for every  , then
, then 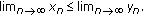
Then we have the following.
-
(a)
For every initial point
 such that the condition (3.2) holds,
such that the condition (3.2) holds, 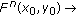
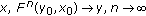 , where
, where  satisfy
satisfy  (3.5)
(3.5)
If  in condition (3.4), then
in condition (3.4), then  If in addition
If in addition  , then
, then  converge to the equilibrium of the equation
converge to the equilibrium of the equation

-
(b)
In particular, every solution
 of
of  (3.7)
(3.7)
such that  converges to the equilibrium of (3.7).
converges to the equilibrium of (3.7).
-
(c)
The following estimates hold:
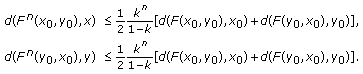 (3.8)
(3.8)
Theorem 3.2.
Assume that along with conditions (i) and (ii) of Theorem 3.1, the following condition is satisfied:
-
(iv)
every pair of elements has either a lower or an upper bound.
Then, the fixed point  is unique and
is unique and 
Remark 3.3.
Theorems 3.1 and 3.2 generalize and extend the results in [14]. The new feature of our results is global attractivity part that extends Theorems 1.1 and 1.2. Most of presented ideas were presented for the first time in [14].
References
Kulenović MRS, Ladas G, Sizer WS: On the recursive sequence .
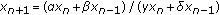 Mathematical Sciences Research Hot-Line 1998,2(5):1–16.
Mathematical Sciences Research Hot-Line 1998,2(5):1–16.Kulenović MRS, Ladas G: Dynamics of Second Order Rational Difference Equations: With Open Problems and Conjecture. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2002:xii+218.
Kulenović MRS, Merino O: A global attractivity result for maps with invariant boxes. Discrete and Continuous Dynamical Systems. Series B 2006,6(1):97–110.
Nussbaum RD: Global stability, two conjectures and Maple. Nonlinear Analysis: Theory, Methods & Applications 2007,66(5):1064–1090. 10.1016/j.na.2006.01.005
Smith HL: The discrete dynamics of monotonically decomposable maps. Journal of Mathematical Biology 2006,53(4):747–758. 10.1007/s00285-006-0004-3
Smith HL: Global stability for mixed monotone systems. Journal of Difference Equations and Applications 2008,14(10–11):1159–1164. 10.1080/10236190802332126
Camouzis E, Ladas G: Dynamics of Third-Order Rational Difference Equations with Open Problems and Conjectures, Advances in Discrete Mathematics and Applications. Volume 5. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2008:xxii+554.
Gibbons CH, Kulenović MRS, Ladas G: On the recursive sequence .
 Mathematical Sciences Research Hot-Line 2000,4(2):1–11.
Mathematical Sciences Research Hot-Line 2000,4(2):1–11.Gibbons CH, Kulenović MRS, Ladas G, Voulov HD: On the trichotomy character of .
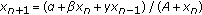 Journal of Difference Equations and Applications 2002,8(1):75–92. 10.1080/10236190211940
Journal of Difference Equations and Applications 2002,8(1):75–92. 10.1080/10236190211940Grove EA, Ladas G: Periodicities in Nonlinear Difference Equations, Advances in Discrete Mathematics and Applications. Volume 4. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2005:xiv+379.
Kulenović MRS, Merino O: Discrete Dynamical Systems and Difference Equations with Mathematica. Chapman & Hall/CRC, Boca Raton, Fla, USA; 2002:xvi+344.
Kulenović MRS, Nurkanovic M: Asymptotic behavior of a system of linear fractional difference equations. Journal of Inequalities and Applications 2005,2005(2):127–143. 10.1155/JIA.2005.127
Agarwal RP, El-Gebeily MA, O'Regan D: Generalized contractions in partially ordered metric spaces. Applicable Analysis 2008,87(1):109–116. 10.1080/00036810701556151
Gnana Bhaskar T, Lakshmikantham V: Fixed point theorems in partially ordered metric spaces and applications. Nonlinear Analysis: Theory, Methods & Applications 2006,65(7):1379–1393. 10.1016/j.na.2005.10.017
Nieto JJ, Rodríguez-López R: Existence and uniqueness of fixed point in partially ordered sets and applications to ordinary differential equations. Acta Mathematica Sinica 2007,23(12):2205–2212. 10.1007/s10114-005-0769-0
Nieto JJ, Rodríguez-López R: Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations. Order 2005,22(3):223–239. 10.1007/s11083-005-9018-5
Nieto JJ, Pouso RL, Rodríguez-López R: Fixed point theorems in ordered abstract spaces. Proceedings of the American Mathematical Society 2007,135(8):2505–2517. 10.1090/S0002-9939-07-08729-1
O'Regan D, Petruşel A: Fixed point theorems for generalized contractions in ordered metric spaces. Journal of Mathematical Analysis and Applications 2008,341(2):1241–1252. 10.1016/j.jmaa.2007.11.026
Petruşel A, Rus IA: Fixed point theorems in ordered -spaces. Proceedings of the American Mathematical Society 2006,134(2):411–418.
Ran ACM, Reurings MCB: A fixed point theorem in partially ordered sets and some applications to matrix equations. Proceedings of the American Mathematical Society 2004,132(5):1435–1443. 10.1090/S0002-9939-03-07220-4
Ahmad B, Nieto JJ: The monotone iterative technique for three-point second-order integrodifferential boundary value problems with -Laplacian. Boundary Value Problems 2007, 2007:-9.
Su Y, Wang D, Shang M: Strong convergence of monotone hybrid algorithm for hemi-relatively nonexpansive mappings. Fixed Point Theory and Applications 2008, 2008:-8.
Xian X, O'Regan D, Agarwal RP: Multiplicity results via topological degree for impulsive boundary value problems under non-well-ordered upper and lower solution conditions. Boundary Value Problems 2008, 2008:-21.
Kulenović MRS, Merino O: Competitive-exclusion versus competitive-coexistence for systems in the plane. Discrete and Continuous Dynamical Systems. Series B 2006,6(5):1141–1156.
Smith HL: Planar competitive and cooperative difference equations. Journal of Difference Equations and Applications 1998,3(5–6):335–357. 10.1080/10236199708808108
Acknowledgment
The authors are grateful to the referees for pointing out few fine details that improved the presented results.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Burgić, D., Kalabušić, S. & Kulenović, M.R.S. Global Attractivity Results for Mixed-Monotone Mappings in Partially Ordered Complete Metric Spaces. Fixed Point Theory Appl 2009, 762478 (2009). https://doi.org/10.1155/2009/762478
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/762478
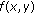 is nondecreasing in
is nondecreasing in  for each
for each  , and
, and 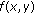 is nonincreasing in
is nonincreasing in  for each
for each 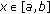 ;
;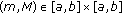 is a solution of the system
is a solution of the system 
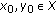 such that the following condition holds:
such that the following condition holds: 
 is a nondecreasing convergent sequence such that
is a nondecreasing convergent sequence such that 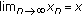 , then
, then 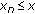 , for all
, for all 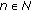 and if
and if  is a nonincreasing convergent sequence such that
is a nonincreasing convergent sequence such that  , then
, then 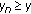 , for all
, for all 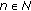 ; if
; if 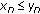 for every
for every  , then
, then 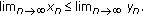
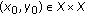 such that condition (2.5) holds,
such that condition (2.5) holds,  , where
, where 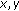 satisfy
satisfy 
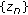 of
of 
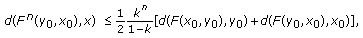
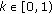 with
with 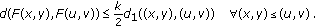
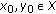 such that the following condition holds:
such that the following condition holds: 
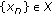 is a nondecreasing convergent sequence such that
is a nondecreasing convergent sequence such that  , then
, then  , for all
, for all 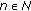 and if
and if 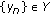 is a nonincreasing convergent sequence such that
is a nonincreasing convergent sequence such that  , then
, then  , for all
, for all  ; if
; if 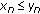 for every
for every  , then
, then 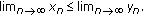
 such that the condition (3.2) holds,
such that the condition (3.2) holds, 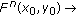
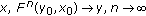 , where
, where  satisfy
satisfy 
 of
of 
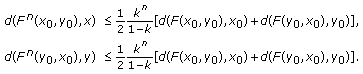
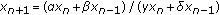 Mathematical Sciences Research Hot-Line 1998,2(5):1–16.
Mathematical Sciences Research Hot-Line 1998,2(5):1–16. Mathematical Sciences Research Hot-Line 2000,4(2):1–11.
Mathematical Sciences Research Hot-Line 2000,4(2):1–11.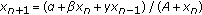 Journal of Difference Equations and Applications 2002,8(1):75–92. 10.1080/10236190211940
Journal of Difference Equations and Applications 2002,8(1):75–92. 10.1080/10236190211940