- Research Article
- Open access
- Published:
Approximate Fixed Point Theorems for the Class of Almost 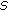 -
- Mappings in Abstract Convex Uniform Spaces
Mappings in Abstract Convex Uniform Spaces
Fixed Point Theory and Applications volume 2009, Article number: 791514 (2009)
Abstract
We use a concept of abstract convexity to define the almost  -
- property, al-
property, al- -
- family, and almost
family, and almost  -spaces. We get some new approximate fixed point theorems and fixed point theorems in almost
-spaces. We get some new approximate fixed point theorems and fixed point theorems in almost  -spaces. Our results extend some results of other authors.
-spaces. Our results extend some results of other authors.
1. Introduction and Preliminaries
In 1929, Knaster et al. [1] proved the well-known  theorem for an
theorem for an  -simplex. Ky Fan's generalization of the
-simplex. Ky Fan's generalization of the  theorem to infinite dimensional topological vector spaces in 1961 [2] proved to be a very versatile tool in modern nonlinear analysis with many far-reaching applications.
theorem to infinite dimensional topological vector spaces in 1961 [2] proved to be a very versatile tool in modern nonlinear analysis with many far-reaching applications.
Chang and Yen [3] undertook a systematic study of the  property, and Chang et al. [4] generalized this property as well as the notion of a
property, and Chang et al. [4] generalized this property as well as the notion of a  family of [4] to the wider concepts of the
family of [4] to the wider concepts of the  -
- property and its related
property and its related  -
- family.
family.
Among the many contributions in the study of the  property and related topics, we mention the work by Amini et al. [5] where the classes of
property and related topics, we mention the work by Amini et al. [5] where the classes of  and
and  -
- mappings have been introduced in the framework of abstract convex spaces. The authors of [5] also define a concept of convexity that contains a number of other concepts of abstract convexities and obtain fixed point theorems for multifunctions verifying the
mappings have been introduced in the framework of abstract convex spaces. The authors of [5] also define a concept of convexity that contains a number of other concepts of abstract convexities and obtain fixed point theorems for multifunctions verifying the  -
- property on
property on  -spaces that extend results of Ben-El-Mechaiekh et al. [6] and Horvath [7], motivated by the works of Ky Fan [2] and Browder [8]. We refer for the study of these notions to Ben-El-Mechaiekh et al. [9], and more recently, to Park [10], and Kim and Park [11].
-spaces that extend results of Ben-El-Mechaiekh et al. [6] and Horvath [7], motivated by the works of Ky Fan [2] and Browder [8]. We refer for the study of these notions to Ben-El-Mechaiekh et al. [9], and more recently, to Park [10], and Kim and Park [11].
In this paper, we use a concept of abstract convexity to define the almost  -
- property, the corresponding notion of almost
property, the corresponding notion of almost  -
- family as well as the concept of almost
family as well as the concept of almost  -spaces.
-spaces.
Let  and
and  be two sets, and let
be two sets, and let  be a set-valued mapping. We will use the following notations in the sequel;
be a set-valued mapping. We will use the following notations in the sequel;
(i)
(ii)
(iii)
(iv) and
and
(v)if  is a nonempty subset of
is a nonempty subset of  , then
, then  denotes the class of all nonempty finite subsets of
denotes the class of all nonempty finite subsets of  .
.
For the case where  and
and  are two topological spaces, a set-valued map
are two topological spaces, a set-valued map  is said to be closed if its graph
is said to be closed if its graph  is closed.
is closed.  is said to be compact if the image
is said to be compact if the image  of
of  under
under  is contained in a compact subset of
is contained in a compact subset of  .
.
Definition 1.1.
An abstract convex space  consists of a nonempty topological space
consists of a nonempty topological space  , and a family
, and a family  of subsets of
of subsets of  such that
such that  and
and  belong to
belong to  and
and  is closed under arbitrary intersection. This kind of abstract convexity was widely studied; see [5, 9, 12, 13].
is closed under arbitrary intersection. This kind of abstract convexity was widely studied; see [5, 9, 12, 13].
Suppose that  is a nonempty subset of an abstract convex space
is a nonempty subset of an abstract convex space  . Then
. Then
(i)a natural definition of  -convex hull of
-convex hull of  is
is

(ii)we say that  is
is  -convex if for each
-convex if for each  ,
,  .
.
Remark 1.2.
It is clear that if  , then
, then  is
is  -convex. That is, each member of
-convex. That is, each member of  is
is  -convex.
-convex.
Definition 1.3.
We list some properties of a uniform space. A uniformity [14] for a set  is a nonempty family
is a nonempty family  of subsets of
of subsets of  such that
such that
(i)each member of  contains the diagonal
contains the diagonal  where the diagonal
where the diagonal  denotes the set of all pairs
denotes the set of all pairs  for
for  in
in  ;
;
(ii)if  , then
, then  ;
;
(iii)if  , then
, then  for some
for some  ;
;
(iv)if  , then
, then  ;
;
(v)if  and
and  , then
, then  .
.
The pair  is called a uniform space. Every member
is called a uniform space. Every member  in
in  is called an entourage. An entourage is said to be symmetric if
is called an entourage. An entourage is said to be symmetric if  whenever
whenever  .
.
Definition 1.4.
If  is an abstract convex space with a uniformity
is an abstract convex space with a uniformity  , then we say that
, then we say that  is an abstract convex uniform space.
is an abstract convex uniform space.
Definition 1.5.
Let  be a nonempty subset of an abstract convex uniform space
be a nonempty subset of an abstract convex uniform space  which has a uniformity
which has a uniformity  , and
, and  has a symmetric basis
has a symmetric basis  . Then
. Then  is called almost
is called almost  -convex if, for any
-convex if, for any  and for any
and for any  , there exists a mapping
, there exists a mapping  such that
such that  for all
for all  and
and  . Moreover, we call the mapping
. Moreover, we call the mapping  a
a  -convex-inducing mapping.
-convex-inducing mapping.
Remark 1.6.
It is clear that every  -convex set must be almost
-convex set must be almost  -convex, but the converse is not true. And in general, the
-convex, but the converse is not true. And in general, the  -convex-inducing mapping is not unique. If
-convex-inducing mapping is not unique. If  and
and  , then
, then  can be regarded as
can be regarded as  . If
. If  , then
, then  can be regarded as
can be regarded as  .
.
Recently, Amini et al. [5] introduced the class of multifunctions with the  property in abstract convex spaces.
property in abstract convex spaces.
Definition 1.7 (see [5]).
Let  be a nonempty set,
be a nonempty set,  an abstract convex space, and
an abstract convex space, and  a topological space. If
a topological space. If  ,
,  and
and  are three multifunctions satisfying
are three multifunctions satisfying

then  is called a
is called a  -
- mapping with respect to
mapping with respect to  . If the multifunction
. If the multifunction  satisfies the requirement that for any
satisfies the requirement that for any  -
- mapping
mapping  with respect to
with respect to  , the family
, the family  has the finite intersection property where
has the finite intersection property where  denotes the closure of
denotes the closure of  , then
, then  is said to have the
is said to have the  -
- property with respect to
property with respect to  . We define
. We define

We extended the  property to the almost
property to the almost  property, as follows.
property, as follows.
Definition 1.8.
Let  be a nonempty set, let
be a nonempty set, let  be an almost
be an almost  -convex subset of an abstract convex uniform space
-convex subset of an abstract convex uniform space  which has a uniformity
which has a uniformity  and
and  has a symmetric basis
has a symmetric basis  , and let
, and let  be a topological space. If
be a topological space. If  ,
,  and
and  are three multifunctions satisfying for each
are three multifunctions satisfying for each  , each
, each  , and each
, and each  , there exists a
, there exists a  -convex-inducing mapping
-convex-inducing mapping  such that
such that

then  is called an almost
is called an almost  -
- mapping with respect to
mapping with respect to  . If the multifunction
. If the multifunction  satisfies the requirement that for any almost
satisfies the requirement that for any almost  -
- mapping
mapping  with respect to
with respect to  , the family
, the family  has the finite intersection property, then
has the finite intersection property, then  is said to have the almost
is said to have the almost  -
- property with respect to
property with respect to  . We define
. We define

From the above definitions, we have the following proposition of the  family.
family.
Proposition 1.9.
Let  be a nonempty set, let
be a nonempty set, let  be an almost
be an almost  -convex subset of an abstract convex uniform space
-convex subset of an abstract convex uniform space  , let
, let  and
and  be two topological spaces, and let
be two topological spaces, and let  be a multifunction. If
be a multifunction. If  and if
and if  is continuous, then
is continuous, then 
The  -mappings and the
-mappings and the  -spaces, in an abstract convex space setting, were also introduced by Amini et al. [5].
-spaces, in an abstract convex space setting, were also introduced by Amini et al. [5].
Definition 1.10 (see [5]).
Let  be an abstract convex space, and
be an abstract convex space, and  a topological space.
a topological space.  map
map  is called a
is called a  -mapping if there exists a multifunction
-mapping if there exists a multifunction  such that
such that
(i)for each  ,
,  implies
implies  , and
, and
(ii) .
.
The mapping  is called a companion mapping of
is called a companion mapping of  .
.
Furthermore, if the abstract convex space  which has a uniformity
which has a uniformity  and
and  has a symmetric basis
has a symmetric basis  , then
, then  is called a
is called a  -space if for each entourage
-space if for each entourage  , there exists a
, there exists a  -mapping
-mapping  such that
such that  .
.
Remark 1.11.
(i)If  is a
is a  -mapping, then for each nonempty subset
-mapping, then for each nonempty subset  of
of  ,
,  is also a
is also a  -mapping.
-mapping.
(ii)It is easy to see that if  and
and  , then
, then  is also a
is also a  -space.
-space.
In order to establish the main result of this paper for the multifunctions with the almost  property, we need the following definitions concerning the almost
property, we need the following definitions concerning the almost  -mappings and the almost
-mappings and the almost  -spaces.
-spaces.
Definition 1.12.
Let  be an almost
be an almost  -convex subset of an abstract convex uniform space
-convex subset of an abstract convex uniform space  which has a uniformity
which has a uniformity  and
and  has a symmetric base family
has a symmetric base family  , and
, and  a topological space. A map
a topological space. A map  is called an almost
is called an almost  -mapping if there exists a multifunction
-mapping if there exists a multifunction  such that
such that
(i)for each  ,
,  and
and  , there exists a
, there exists a  -convex-inducing
-convex-inducing  such that
such that  , and
, and
(ii)
The mapping  is called an almost companion mapping of
is called an almost companion mapping of  .
.
Furthermore,  is called an almost
is called an almost  -space, if, for each entourage
-space, if, for each entourage  , there exists an almost
, there exists an almost  -mapping
-mapping  such that
such that  .
.
Definition 1.13.
Let  be an almost
be an almost  -space, and let
-space, and let  . We say that
. We say that  has the approximate fixed point property if, for each
has the approximate fixed point property if, for each  , there exists
, there exists  such that
such that  .
.
2. Main Results
Using the above introduced concepts and definitions, we now state our main theorem.
Theorem 2.1.
Let  be an almost
be an almost  -space, and let
-space, and let  be a surjective single-valued function. If
be a surjective single-valued function. If  is compact, then
is compact, then  has the approximate fixed point property.
has the approximate fixed point property.
Proof.
Let  be a symmetric basis of the uniform structure, and let
be a symmetric basis of the uniform structure, and let  . Take
. Take  such that
such that  . Then, by the definition of the almost
. Then, by the definition of the almost  -space, there exists an almsot
-space, there exists an almsot  -mapping
-mapping  such that
such that  . Since
. Since  is an almsot
is an almsot  -mapping, there exists an almost companion mapping
-mapping, there exists an almost companion mapping  such that
such that  .
.
Let  . Then
. Then  is compact, since
is compact, since  is compact. Hence there exists
is compact. Hence there exists  such that
such that  . Since
. Since  is surjective, there exists a finite subset
is surjective, there exists a finite subset  of
of  such that
such that  .
.
Now, we define  by
by

By the definition of  , we obtain that
, we obtain that  is not an almost
is not an almost  mapping with respect to
mapping with respect to  . Hence, there exist
. Hence, there exist  and
and  such that for any
such that for any  -convex-inducing
-convex-inducing  , we have
, we have

So, for any  -convex-inducing
-convex-inducing  , there exist
, there exist  and
and  such that
such that  . Consequently,
. Consequently,  , and so
, and so  for all
for all  . Since
. Since  is an almost
is an almost  -mapping, there exists a
-mapping, there exists a  -convex-inducing
-convex-inducing  such that
such that  . So
. So  and
and  . Thus, there exists
. Thus, there exists  such that
such that  . Since
. Since  is an almost
is an almost  -space, we have
-space, we have  , and so
, and so  , that is,
, that is,  .
.
Therefore,  . The proof is finished.
. The proof is finished.
Remark 2.2.
In the case, if  is a
is a  -space and
-space and  , then the above theorem reduces to Amini et al. [5, Theorem 2.5]
, then the above theorem reduces to Amini et al. [5, Theorem 2.5]
From Theorem 2.1 above, we obtain immediately the following fixed point theorem.
Theorem 2.3.
Suppose that all of the assumptions of Theorem 2.1 hold. If  is closed, then
is closed, then  has a fixed point in
has a fixed point in  .
.
Proof.
By Theorem 2.1, for each  , there exist
, there exist  such that
such that  . Since
. Since  is compact, without loss of generality, we may assume that
is compact, without loss of generality, we may assume that  converges to some
converges to some  in
in  ; then
; then  also converges to
also converges to  since
since  is a Hausdorff uniform space and
is a Hausdorff uniform space and  for each
for each  . By the closedness of
. By the closedness of  , we have that
, we have that  .
.
Corollary 2.4.
Let  be an almost
be an almost  -space, and let
-space, and let  be a surjective single-valued function. Suppose
be a surjective single-valued function. Suppose  such that
such that  is totally bounded. Then
is totally bounded. Then  has the approximate fixed point property.
has the approximate fixed point property.
Corollary 2.5.
Suppose that all of the assumptions of the above Corollary 2.5 hold. If  is closed, then
is closed, then  has a fixed point in
has a fixed point in  .
.
In case  is an almost convex subset of Hausdorff topological vector spaces and for each
is an almost convex subset of Hausdorff topological vector spaces and for each  , we have
, we have
(i) , and
, and
(ii) .
.
This allows us to state the following results.
Theorem 2.6.
Let  be a Hausdorff locally convex space, let
be a Hausdorff locally convex space, let  be an almost convex subset of
be an almost convex subset of  , and let
, and let  be a surjective function. Assume that
be a surjective function. Assume that  is compact and closed, then
is compact and closed, then  has a fixed point in
has a fixed point in  .
.
Proof.
Let  be the family of all convex subsets of
be the family of all convex subsets of  , and let
, and let  be a local basis of
be a local basis of  such that each
such that each  is symmetric and convex for each
is symmetric and convex for each  . For each
. For each  , we set
, we set  . Noting that
. Noting that  . Set
. Set

Then  is a basis of a uniformity of
is a basis of a uniformity of  . For each
. For each  ,
,  , we define the two set-valued mappings
, we define the two set-valued mappings  by
by  for each
for each  . Then we have
. Then we have
-
(i)
for each
 ,
, 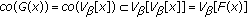 , and
, and
(ii) .
.
So,  is an almost companion mapping of
is an almost companion mapping of  . This implies that
. This implies that  is an almost
is an almost  -mapping such that
-mapping such that  . Therefore,
. Therefore,  is an almost
is an almost  -space.
-space.
All conditions of Theorems 2.1 and 2.3 are therefore fulfilled; the result follows from an argument similar to those in the proofs of Theorems 2.1 and 2.3.
Theorem 2.7.
Let  be a topological vector space, let
be a topological vector space, let  be an almost convex subset of
be an almost convex subset of  , and let
, and let  be a surjective function. Suppose that
be a surjective function. Suppose that  is compact, then for any symmetric convex neighborhood
is compact, then for any symmetric convex neighborhood  of
of  in
in  , there is
, there is  such that
such that  .
.
Proof.
Let  be the family of all convex subsets of
be the family of all convex subsets of  , and let
, and let  be a new local basis of
be a new local basis of  . We will use
. We will use  to construct a weaker topology on
to construct a weaker topology on  such that
such that  becomes a new topological vector space. For each
becomes a new topological vector space. For each  , we set
, we set  . Noting that
. Noting that  . Set
. Set

Then  is a basis of a uniformity of
is a basis of a uniformity of  . In vein of the reasonings similar to those of Theorems 2.1 and 2.6, we complete the proof.
. In vein of the reasonings similar to those of Theorems 2.1 and 2.6, we complete the proof.
References
Knaster B, Kuratowski C, Mazurkiewicz S: Ein Beweis des Fixpunksatzes fur -dimensionale Simplexe. Fundamenta Mathematicae 1929, 14: 132–137.
Fan K: A generalization of Tychonoff's fixed point theorem. Mathematische Annalen 1961, 142: 305–310. 10.1007/BF01353421
Chang T-H, Yen C-L: KKM property and fixed point theorems. Journal of Mathematical Analysis and Applications 1996,203(1):224–235. 10.1006/jmaa.1996.0376
Chang T-H, Huang Y-Y, Jeng J-C: Fixed-point theorems for multifunctions in S-KKM class. Nonlinear Analysis: Theory, Methods & Applications 2001,44(8):1007–1017. 10.1016/S0362-546X(99)00318-1
Amini A, Fakhar M, Zafarani J: Fixed point theorems for the class S-KKM mappings in abstract convex spaces. Nonlinear Analysis: Theory, Methods & Applications 2007,66(1):14–21. 10.1016/j.na.2005.11.005
Ben-El-Mechaiekh H, Deguire P, Granas A: Points fixes et cocidences pour les fonctions multivoques (applications de type et
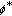 ). II. Comptes Rendus de l'Académie des Sciences 1982,295(5):381–384.
). II. Comptes Rendus de l'Académie des Sciences 1982,295(5):381–384.Horvath CD: Contractibility and generalized convexity. Journal of Mathematical Analysis and Applications 1991,156(2):341–357. 10.1016/0022-247X(91)90402-L
Browder FE: The fixed point theory of multi-valued mappings in topological vector spaces. Mathematische Annalen 1968, 177: 283–301. 10.1007/BF01350721
Ben-El-Mechaiekh H, Chebbi S, Florenzano M, Llinares J-V: Abstract convexity and fixed points. Journal of Mathematical Analysis and Applications 1998,222(1):138–150. 10.1006/jmaa.1998.5918
Park S: Fixed points of better admissible maps on generalized convex spaces. Journal of the Korean Mathematical Society 2000,37(6):885–899.
Kim J-H, Park S: Comments on some fixed point theorems in hyperconvex metric spaces. Journal of Mathematical Analysis and Applications 2004,291(1):154–164. 10.1016/j.jmaa.2003.10.022
Kay DC, Womble EW: Axiomatic convexity theory and relationships between the Caratheodory, Helly, and Radon numbers. Pacific Journal of Mathematics 1971, 38: 471–485.
Llinares J-V: Abstract convexity, some relations and applications. Optimization 2002,51(6):797–818. 10.1080/0233193021000015587
Kelly JL: General Topology. Van Nostrand, Princeton, NJ, USA; 1955.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chang, TH., Chen, CM. & Huang, YH. Approximate Fixed Point Theorems for the Class of Almost 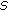 -
- Mappings in Abstract Convex Uniform Spaces.
Fixed Point Theory Appl 2009, 791514 (2009). https://doi.org/10.1155/2009/791514
Mappings in Abstract Convex Uniform Spaces.
Fixed Point Theory Appl 2009, 791514 (2009). https://doi.org/10.1155/2009/791514
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/791514
 ,
, 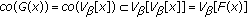 , and
, and ). II. Comptes Rendus de l'Académie des Sciences 1982,295(5):381–384.
). II. Comptes Rendus de l'Académie des Sciences 1982,295(5):381–384.