- Research Article
- Open access
- Published:
An Iterative Algorithm Combining Viscosity Method with Parallel Method for a Generalized Equilibrium Problem and Strict Pseudocontractions
Fixed Point Theory and Applications volume 2009, Article number: 794178 (2009)
Abstract
We introduce a new approximation scheme combining the viscosity method with parallel method for finding a common element of the set of solutions of a generalized equilibrium problem and the set of fixed points of a family of finitely strict pseudocontractions. We obtain a strong convergence theorem for the sequences generated by these processes in Hilbert spaces. Based on this result, we also get some new and interesting results. The results in this paper extend and improve some well-known results in the literature.
1. Introduction
Let  be a real Hilbert space with inner product
be a real Hilbert space with inner product  and induced norm
and induced norm  and let
and let  be a nonempty-closed convex subset of
be a nonempty-closed convex subset of  . Let
. Let  be a function and let
be a function and let  be a bifunction from
be a bifunction from  to
to  such that
such that  , where
, where  is the set of real numbers and
is the set of real numbers and  . Flores-Bazán [1] introduced the following generalized equilibrium problem:
. Flores-Bazán [1] introduced the following generalized equilibrium problem:

The set of solutions of (1.1) is denoted by  . Flores-Bazán [1] provided some characterizations of the nonemptiness of the solution set for problem (1.1) in reflexive Banach spaces in the quasiconvex case. Bigi et al. [2] studied a dual problem associated with the problem (1.1) with
. Flores-Bazán [1] provided some characterizations of the nonemptiness of the solution set for problem (1.1) in reflexive Banach spaces in the quasiconvex case. Bigi et al. [2] studied a dual problem associated with the problem (1.1) with  .
.
Let  . Here
. Here  denotes the indicator function of the set
denotes the indicator function of the set  ; that is,
; that is,  if
if  and
and  otherwise. Then the problem (1.1) becomes the following equilibrium problem:
otherwise. Then the problem (1.1) becomes the following equilibrium problem:

The set of solutions of (1.2) is denoted by  . The problem (1.2) includes, as special cases, the optimization problem, the variational inequality problem, the fixed point problem, the nonlinear complementarity problem, the Nash equilibrium problem in noncooperative games, and the vector optimization problem. For more detail, please see [3–5] and the references therein.
. The problem (1.2) includes, as special cases, the optimization problem, the variational inequality problem, the fixed point problem, the nonlinear complementarity problem, the Nash equilibrium problem in noncooperative games, and the vector optimization problem. For more detail, please see [3–5] and the references therein.
If  for all
for all  , where
, where  is a function, then the problem (1.1) becomes a problem of finding
is a function, then the problem (1.1) becomes a problem of finding  which is a solution of the following minimization problem:
which is a solution of the following minimization problem:

The set of solutions of (1.3) is denoted by  .
.
If  is replaced by a real-valued function
is replaced by a real-valued function  , the problem (1.1) reduces to the following mixed equilibrium problem introduced by Ceng and Yao [6]:
, the problem (1.1) reduces to the following mixed equilibrium problem introduced by Ceng and Yao [6]:

Recall that a mapping  is said to be a
is said to be a  -strict pseudocontraction [7] if there exists
-strict pseudocontraction [7] if there exists  such that
such that

where  denotes the identity operator on
denotes the identity operator on  . When
. When  ,
,  is said to be nonexpansive. Note that the class of strict pseudocontraction mappings strictly includes the class of nonexpansive mappings. We denote the set of fixed points of
is said to be nonexpansive. Note that the class of strict pseudocontraction mappings strictly includes the class of nonexpansive mappings. We denote the set of fixed points of  by
by  .
.
Ceng and Yao [6], Yao et al. [8], and Peng and Yao [9, 10] introduced some iterative schemes for finding a common element of the set of solutions of the mixed equilibrium problem (1.4) and the set of common fixed points of a family of finitely (infinitely) nonexpansive mappings (strict pseudocontractions) in a Hilbert space and obtained some strong convergence theorems(weak convergence theorems). Some methods have been proposed to solve the problem (1.2); see, for instance, [3–5, 11–18] and the references therein. Recently, S. Takahashi and W. Takahashi [12] introduced an iterative scheme by the viscosity approximation method for finding a common element of the set of solutions of problem (1.2) and the set of fixed points of a nonexpansive mapping in a Hilbert space and proved a strong convergence theorem. Su et al. [13] introduced an iterative scheme by the viscosity approximation method for finding a common element of the set of solutions of problem (1.2) and the set of fixed points of a nonexpansive mapping and the set of solutions of the variational inequality problem for an  -inverse strongly monotone mapping in a Hilbert space. Tada and Takahashi [14] introduced two iterative schemes for finding a common element of the set of solutions of problem (1.2) and the set of fixed points of a nonexpansive mapping in a Hilbert space and obtained both strong convergence theorem and weak convergence theorem. Ceng et al. [15] introduced an iterative algorithm for finding a common element of the set of solutions of problem (1.2) and the set of fixed points of a strict pseudocontraction mapping. Chang et al. [16] introduced some iterative processes based on the extragradient method for finding the common element of the set of fixed points of a family of infinitely nonexpansive mappings, the set of problem (1.2), and the set of solutions of a variational inequality problem for an
-inverse strongly monotone mapping in a Hilbert space. Tada and Takahashi [14] introduced two iterative schemes for finding a common element of the set of solutions of problem (1.2) and the set of fixed points of a nonexpansive mapping in a Hilbert space and obtained both strong convergence theorem and weak convergence theorem. Ceng et al. [15] introduced an iterative algorithm for finding a common element of the set of solutions of problem (1.2) and the set of fixed points of a strict pseudocontraction mapping. Chang et al. [16] introduced some iterative processes based on the extragradient method for finding the common element of the set of fixed points of a family of infinitely nonexpansive mappings, the set of problem (1.2), and the set of solutions of a variational inequality problem for an  -inverse strongly monotone mapping. Colao et al. [17] introduced an iterative method for finding a common element of the set of solutions of problem (1.2) and the set of fixed points of a finite family of nonexpansive mappings in a Hilbert space and proved the strong convergence of the proposed iterative algorithm to the unique solution of a variational inequality, which is the optimality condition for a minimization problem. To the best of our knowledge, there is not any algorithms for solving problem (1.1).
-inverse strongly monotone mapping. Colao et al. [17] introduced an iterative method for finding a common element of the set of solutions of problem (1.2) and the set of fixed points of a finite family of nonexpansive mappings in a Hilbert space and proved the strong convergence of the proposed iterative algorithm to the unique solution of a variational inequality, which is the optimality condition for a minimization problem. To the best of our knowledge, there is not any algorithms for solving problem (1.1).
On the other hand, Marino and Xu [19] and Zhou [20] introduced and researched some iterative scheme for finding a fixed point of a strict pseudocontraction mapping. Acedo and Xu [21] introduced some parallel and cyclic algorithms for finding a common fixed point of a family of finite strict pseudocontraction mappings and obtained both weak and strong convergence theorems for the sequences generated by the iterative schemes.
In the present paper, we introduce a new approximation scheme combining the viscosity method with parallel method for finding a common element of the set of solutions of the generalized equilibrium problem and the set of fixed points of a family of finitely strict pseudocontractions. We obtain a strong convergence theorem for the sequences generated by these processes. Based on this result, we also get some new and interesting results. The results in this paper extend and improve some well-known results in the literature.
2. Preliminaries
Let  be a real Hilbert space with inner product
be a real Hilbert space with inner product  and norm
and norm  . Let
. Let  be a nonempty-closed convex subset of
be a nonempty-closed convex subset of  . Let symbols
. Let symbols  and
and  denote strong and weak convergences, respectively. In a real Hilbert space
denote strong and weak convergences, respectively. In a real Hilbert space  , it is well known that
, it is well known that

for all  and
and  .
.
For any  , there exists a unique nearest point in
, there exists a unique nearest point in  , denoted by
, denoted by  , such that
, such that  for all
for all  . The mapping
. The mapping  is called the metric projection of
is called the metric projection of  onto
onto  . We know that
. We know that  is a nonexpansive mapping from
is a nonexpansive mapping from  onto
onto  . It is also known that
. It is also known that  and
and

for all  and
and  .
.
For each  , we denote by
, we denote by  the convex hull of
the convex hull of  . A multivalued mapping
. A multivalued mapping  is said to be a KKM map if, for every finite subset
is said to be a KKM map if, for every finite subset  ,
, 
We will use the following results in the sequel.
Lemma 2.1 (see [22]).
Let  be a nonempty subset of a Hausdorff topological vector space
be a nonempty subset of a Hausdorff topological vector space  and let
and let  be a KKM map. If
be a KKM map. If  is closed for all
is closed for all  and is compact for at least one
and is compact for at least one  , then
, then 
For solving the generalized equilibrium problem, let us give the following assumptions for the bifunction  ,
,  and the set
and the set  :
:
(A1) for all
for all  ;
;
(A2) is monotone, that is,
is monotone, that is,  for any
for any  ;
;
(A3) for each  ,
,  is weakly upper semicontinuous;
is weakly upper semicontinuous;
(A4)for each  is convex;
is convex;
(A5)for each  is lower semicontinuous;
is lower semicontinuous;
(B1)For each  and
and  , there exist a bounded subset
, there exist a bounded subset  and
and  such that for any
such that for any  ,
,

(B2) is a bounded set.
is a bounded set.
Lemma 2.2.
Let  be a nonempty-closed convex subset of
be a nonempty-closed convex subset of  . Let
. Let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4) and let
satisfying (A1)–(A4) and let  be a proper lower semicontinuous and convex function such that
be a proper lower semicontinuous and convex function such that  . For
. For  and
and  define a mapping
define a mapping  as follows:
as follows:

for all  . Assume that either (B1) or (B2) holds. Then, the following conclusions hold:
. Assume that either (B1) or (B2) holds. Then, the following conclusions hold:
(1)for each  ,
,  ;
;
(2) is single-valued;
is single-valued;
(3) is firmly nonexpansive, that is, for any
is firmly nonexpansive, that is, for any 

(4)
(5) is closed and convex.
is closed and convex.
Proof.
Let  be any given point in
be any given point in  . For each
. For each  , we define
, we define

Note that for each  ,
,  is nonempty since
is nonempty since  and for each
and for each  ,
,  . We will prove that
. We will prove that  is a KKM map on
is a KKM map on  . Suppose that there exists a finite subset
. Suppose that there exists a finite subset  of
of  and
and  for all
for all  with
with  such that
such that  for each
for each  . Then we have
. Then we have

for each  . By (A4) and the convexity of
. By (A4) and the convexity of  , we have
, we have

which is a contradiction. Hence,  is a KKM map on
is a KKM map on  . Note that
. Note that  (the weak closure of
(the weak closure of  ) is a weakly closed subset of
) is a weakly closed subset of  for each
for each  . Moreover, if (B2) holds, then
. Moreover, if (B2) holds, then  is also weakly compact for each
is also weakly compact for each  . If (B1) holds, then for
. If (B1) holds, then for  , there exists a bounded subset
, there exists a bounded subset  and
and  such that for any
such that for any  ,
,

This shows that

Hence,  is weakly compact. Thus, in both cases, we can use Lemma 2.1 and have
is weakly compact. Thus, in both cases, we can use Lemma 2.1 and have  .
.
Next, we will prove that  for each
for each  ; that is,
; that is,  is weakly closed. Let
is weakly closed. Let  and let
and let  be a sequence in
be a sequence in  such that
such that  . Then,
. Then,

Since  is weakly lower semicontinuous, we can show that
is weakly lower semicontinuous, we can show that

It follows from (A3) and the weak lower semicontinuity of  that
that

This implies that  . Hence,
. Hence,  is weakly closed. Hence,
is weakly closed. Hence,  . Hence, from the arbitrariness of
. Hence, from the arbitrariness of  , we conclude that
, we conclude that  ,
,  .
.
We observe that  . So by similar argument with that in the proof of Lemma 2.3 in [9], we can easily show that
. So by similar argument with that in the proof of Lemma 2.3 in [9], we can easily show that  is single-valued and
is single-valued and  is a firmly nonexpansive-type map. Next, we claim that
is a firmly nonexpansive-type map. Next, we claim that  . Indeed, we have the following:
. Indeed, we have the following:

At last, we claim that  is a closed convex. Indeed, Since
is a closed convex. Indeed, Since  is firmly nonexpansive,
is firmly nonexpansive,  is also nonexpansive. By [23, Proposition 5.3], we know that
is also nonexpansive. By [23, Proposition 5.3], we know that  is closed and convex.
is closed and convex.
Remark 2.3.
It is easy to see that Lemma 2.2 is a generalization of [9, Lemma 2.3].
Assume that  is a sequence of nonnegative real numbers such that
is a sequence of nonnegative real numbers such that

where  is a sequence in
is a sequence in  and
and  is a sequence such that
is a sequence such that

Then, 
Lemma 2.5.
In a real Hilbert space  , there holds the following inequality:
, there holds the following inequality:

for all 
3. Strong Convergence Theorems
In this section, we show a strong convergence of an iterative algorithm based on both viscosity approximation method and parallel method which solves the problem of finding a common element of the set of solutions of a generalized equilibrium problem and the set of fixed points of a family of finitely strict pseudocontractions in a Hilbert space.
We need the following assumptions for the parameters 
 and
and  :
:
(C1) and
and  ;
;
(C2) ;
;
(C3) for some
for some  and
and  ;
;
(C4) and
and  ;
;
(C5) for all
for all  .
.
Theorem 3.1.
Let  be a nonempty-closed convex subset of a real Hilbert space
be a nonempty-closed convex subset of a real Hilbert space  . Let
. Let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A5), and let
satisfying (A1)–(A5), and let  be a proper lower semicontinuous and convex function such that
be a proper lower semicontinuous and convex function such that  . Let
. Let  be an integer. For each
be an integer. For each  , let
, let  be an
be an  -strict pseudocontraction for some
-strict pseudocontraction for some  such that
such that  . Assume for each
. Assume for each  ,
,  is a finite sequence of positive numbers such that
is a finite sequence of positive numbers such that  for all
for all  and
and  for all
for all  . Let
. Let  . Assume that either (B1) or (B2) holds. Let
. Assume that either (B1) or (B2) holds. Let  be a contraction of
be a contraction of  into itself and let
into itself and let  ,
,  and
and  be sequences generated by
be sequences generated by

for every  , where
, where  and
and  are sequences of numbers satisfying the conditions (C1)–(C5). Then,
are sequences of numbers satisfying the conditions (C1)–(C5). Then,  ,
,  and
and  converge strongly to
converge strongly to  .
.
Proof.
We show that  is a contraction of
is a contraction of  into itself. In fact, there exists
into itself. In fact, there exists  such that
such that  for all
for all  . So, we have
. So, we have

for all  Since
Since  is complete, there exists a unique element
is complete, there exists a unique element  such that
such that  .
.
Let  and let
and let  be a sequence of mappings defined as in Lemma 2.2. From
be a sequence of mappings defined as in Lemma 2.2. From  , we have
, we have

We define a mapping  by
by

By [21, Proposition 2.6], we know that  is an
is an  -strict pseudocontraction and
-strict pseudocontraction and  . It follows from (3.3),
. It follows from (3.3),  and
and  such that
such that

Put  It is obvious that
It is obvious that  Suppose
Suppose  From (3.3), (3.5), and
From (3.3), (3.5), and  , we have
, we have

for every  Therefore,
Therefore,  is bounded. From (3.3) and (3.5), we also obtain that
is bounded. From (3.3) and (3.5), we also obtain that  and
and  are bounded.
are bounded.
Following [26], define  by
by

As shown in [26], each  is a nonexpansive mapping on
is a nonexpansive mapping on  . Set
. Set  , we have
, we have

On the other hand, from  and
and  , we have
, we have


Putting  in (3.9) and
in (3.9) and  in (3.10), we have
in (3.10), we have

So, from the monotonicity of  , we get
, we get

hence

Without loss of generality, let us assume that there exists a real number  such that
such that  for all
for all  Then,
Then,

hence

where 
It follows from (3.8) and (3.15) that

Define a sequence  such that
such that

Then, we have

From (3.18) and (3.16), we have

It follows from (C1)–(C5) that

Hence, by [27, Lemma 2.2], we have  . Consequently,
. Consequently,

Since  , we have
, we have

thus

It follows from (C1) and (C2) that  .
.
Since  for
for  , it follows from (3.5) and (3.3) that
, it follows from (3.5) and (3.3) that

from which it follows that

It follows from (C1)–(C3) and  that
that

For  , we have from Lemma 2.2,
, we have from Lemma 2.2,

Hence,

By (3.24) and (3.28), we have

Hence,

It follows from (C1), (C2), and  that
that  .
.
Next, we show that

where  . To show this inequality, we can choose a subsequence
. To show this inequality, we can choose a subsequence  of
of  such that
such that

Since  is bounded, there exists a subsequence
is bounded, there exists a subsequence  of
of  which converges weakly to
which converges weakly to  . Without loss of generality, we can assume that
. Without loss of generality, we can assume that  From
From  , we obtain that
, we obtain that  . From
. From  , we also obtain that
, we also obtain that  . Since
. Since  and
and  is closed and convex, we obtain
is closed and convex, we obtain  .
.
We first show that  To see this, we observe that we may assume (by passing to a further subsequence if necessary)
To see this, we observe that we may assume (by passing to a further subsequence if necessary)  (as
(as  ) for
) for  It is easy to see that
It is easy to see that  and
and  . We also have
. We also have

where  . Note that by [21, Proposition 2.6],
. Note that by [21, Proposition 2.6],  is an
is an  -strict pseudocontraction and
-strict pseudocontraction and  . Since
. Since

it follows from (3.26) and  that
that

So by the demiclosedness principle [21, Proposition 2.6(ii)], it follows that  .
.
We now show  By
By  we know that
we know that

It follows from (A2) that

Hence,

It follows from (A4), (A5) and the weakly lower semicontinuity of  ,
,  and
and  that
that

For  with
with  and
and  , let
, let  Since
Since  and
and  , we obtain
, we obtain  and hence
and hence  . So by (A4) and the convexity of
. So by (A4) and the convexity of  , we have
, we have

Dividing by  , we get
, we get

Letting  , it follows from (A3) and the weakly lower semicontinuity of
, it follows from (A3) and the weakly lower semicontinuity of  that
that

for all  . Observe that if
. Observe that if  , then
, then  holds. Moreover, hence
holds. Moreover, hence  . This implies
. This implies  Therefore, we have
Therefore, we have

Finally, we show that  , where
, where  .
.
From Lemma 2.5, we have

thus

It follows from (C1), (3.43), (3.45), and Lemma 2.4 that  . From
. From  and
and  , we have
, we have  and
and  . The proof is now complete.
. The proof is now complete.
Theorem 3.2.
Let  be a nonempty-closed convex subset of a real Hilbert space
be a nonempty-closed convex subset of a real Hilbert space  . Let
. Let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A5), and let
satisfying (A1)–(A5), and let  be a proper lower semicontinuous and convex function such that
be a proper lower semicontinuous and convex function such that  . Let
. Let  be an integer. For each
be an integer. For each  , let
, let  be an
be an  -strict pseudocontraction for some
-strict pseudocontraction for some  such that
such that  . Assume for each
. Assume for each  ,
,  is a finite sequence of positive numbers such that
is a finite sequence of positive numbers such that  for all
for all  and
and  for all
for all  . Let
. Let  . Assume that either (B1) or (B2) holds. Let
. Assume that either (B1) or (B2) holds. Let  be an arbitrary point in
be an arbitrary point in  and let
and let  ,
,  and
and  be sequences generated by
be sequences generated by

for every  where
where  and
and  are sequences of numbers satisfying the conditions (C1)–(C5). Then,
are sequences of numbers satisfying the conditions (C1)–(C5). Then,  ,
,  and
and  converge strongly to
converge strongly to  .
.
Proof.
Let  for all
for all  , by Theorem 3.1, we obtain the desired result.
, by Theorem 3.1, we obtain the desired result.
4. Applications
By Theorems 3.1 and 3.2, we can obtain many new and interesting strong convergence theorems. Now, give some examples as follows: for  , let
, let  , by Theorems 3.1 and 3.2, respectively, we have the following results.
, by Theorems 3.1 and 3.2, respectively, we have the following results.
Theorem 4.1.
Let  be a nonempty-closed convex subset of a real Hilbert space
be a nonempty-closed convex subset of a real Hilbert space  . Let
. Let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A5), and let
satisfying (A1)–(A5), and let  be a proper lower semicontinuous and convex function such that
be a proper lower semicontinuous and convex function such that  . Let
. Let  be an
be an  -strict pseudocontraction for some
-strict pseudocontraction for some  such that
such that  . Assume that either (B1) or (B2) holds. Let
. Assume that either (B1) or (B2) holds. Let  be a contraction of
be a contraction of  into itself and let
into itself and let  ,
,  and
and  be sequences generated by
be sequences generated by

for every  where
where  ,
,  ,
,  and
and  are sequences of numbers satisfying the conditions (C1)–(C4). Then,
are sequences of numbers satisfying the conditions (C1)–(C4). Then,  ,
,  and
and  converge strongly to
converge strongly to  .
.
Theorem 4.2.
Let  be a nonempty-closed convex subset of a real Hilbert space
be a nonempty-closed convex subset of a real Hilbert space  . Let
. Let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A5), and let
satisfying (A1)–(A5), and let  be a proper lower semicontinuous and convex function such that
be a proper lower semicontinuous and convex function such that  . Let
. Let  be an
be an  -strict pseudocontraction for some
-strict pseudocontraction for some  such that
such that  . Assume that either (B1) or (B2) holds. Let
. Assume that either (B1) or (B2) holds. Let  be an arbitrary point in
be an arbitrary point in  and let
and let  ,
,  and
and  be sequences generated by
be sequences generated by

for every  where
where  ,
,  ,
,  and
and  are sequences of numbers satisfying the conditions (C1)–(C4). Then,
are sequences of numbers satisfying the conditions (C1)–(C4). Then,  ,
,  and
and  converge strongly to
converge strongly to  .
.
We need the following two assumptions.
(B3)For each  and
and  , there exist a bounded subset
, there exist a bounded subset  and
and  such that for any
such that for any  ,
,

(B4)For each  and
and  , there exist a bounded subset
, there exist a bounded subset  and
and  such that for any
such that for any  ,
,

Let  , by Theorems 3.1 and 3.2, respectively, we obtain the following results.
, by Theorems 3.1 and 3.2, respectively, we obtain the following results.
Theorem 4.3.
Let  be a nonempty-closed convex subset of a real Hilbert space
be a nonempty-closed convex subset of a real Hilbert space  . Let
. Let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A5). Let
satisfying (A1)–(A5). Let  be an integer. For each
be an integer. For each  , let
, let  be an
be an  -strict pseudocontraction for some
-strict pseudocontraction for some  such that
such that  . Assume for each
. Assume for each  ,
,  is a finite sequence of positive numbers such that
is a finite sequence of positive numbers such that  for all
for all  and
and  for all
for all  . Let
. Let  . Assume that either (B3) or (B2) holds. Let
. Assume that either (B3) or (B2) holds. Let  be a contraction of
be a contraction of  into itself, and let
into itself, and let  ,
,  and
and  be sequences generated by
be sequences generated by

for every  where
where  and
and  are sequences of numbers satisfying the conditions (C1)–(C5). Then,
are sequences of numbers satisfying the conditions (C1)–(C5). Then,  ,
,  and
and  converge strongly to
converge strongly to  .
.
Theorem 4.4.
Let  be a nonempty-closed convex subset of a real Hilbert space
be a nonempty-closed convex subset of a real Hilbert space  . Let
. Let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A5). Let
satisfying (A1)–(A5). Let  be an integer. For each
be an integer. For each  , let
, let  be an
be an  -strict pseudocontraction for some
-strict pseudocontraction for some  such that
such that  . Assume for each
. Assume for each  ,
,  is a finite sequence of positive numbers such that
is a finite sequence of positive numbers such that  for all
for all  and
and  for all
for all  . Let
. Let  . Assume that either (B3) or (B2) holds. Let
. Assume that either (B3) or (B2) holds. Let  be an arbitrary point in
be an arbitrary point in  and let
and let  ,
,  and
and  be sequences generated by
be sequences generated by

for every  where
where  and
and  are sequences of numbers satisfying the conditions (C1)–(C5). Then,
are sequences of numbers satisfying the conditions (C1)–(C5). Then,  ,
,  and
and  converge strongly to
converge strongly to  .
.
Let  for all
for all  , by Theorems 3.1 and 3.2, respectively, we obtain the following results.
, by Theorems 3.1 and 3.2, respectively, we obtain the following results.
Theorem 4.5.
Let  be a nonempty-closed convex subset of a real Hilbert space
be a nonempty-closed convex subset of a real Hilbert space  . Let
. Let  be a lower semicontinuous and convex function, and let
be a lower semicontinuous and convex function, and let  be a proper lower semicontinuous and convex function such that
be a proper lower semicontinuous and convex function such that  . Let
. Let  be an integer. For each
be an integer. For each  , let
, let  be an
be an  -strict pseudocontraction for some
-strict pseudocontraction for some  such that
such that  . Assume for each
. Assume for each  ,
,  is a finite sequence of positive numbers such that
is a finite sequence of positive numbers such that  for all
for all  and
and  for all
for all  . Let
. Let  . Assume that either (B4) or (B2) holds. Let
. Assume that either (B4) or (B2) holds. Let  be a contraction of
be a contraction of  into itself, and let
into itself, and let  ,
,  and
and  be sequences generated by
be sequences generated by

for every  , where
, where  and
and  are sequences of numbers satisfying the conditions (C1)–(C5). Then,
are sequences of numbers satisfying the conditions (C1)–(C5). Then,  ,
,  and
and  converge strongly to
converge strongly to  .
.
Theorem 4.6.
Let  be a nonempty-closed convex subset of a real Hilbert space
be a nonempty-closed convex subset of a real Hilbert space  . Let
. Let  be a lower semicontinuous and convex function, and let
be a lower semicontinuous and convex function, and let  be a proper lower semicontinuous and convex function such that
be a proper lower semicontinuous and convex function such that  . Let
. Let  be an integer. For each
be an integer. For each  , let
, let  be an
be an  -strict pseudocontraction for some
-strict pseudocontraction for some  such that
such that  . Assume for each
. Assume for each  ,
,  is a finite sequence of positive numbers such that
is a finite sequence of positive numbers such that  for all
for all  and
and  for all
for all  . Let
. Let  . Assume that either (B4) or (B2) holds. Let
. Assume that either (B4) or (B2) holds. Let  be an arbitrary point in
be an arbitrary point in  and let
and let  ,
,  and
and  be sequences generated by
be sequences generated by

for every  where
where  and
and  are sequences of numbers satisfying the conditions (C1)–(C5). Then,
are sequences of numbers satisfying the conditions (C1)–(C5). Then,  ,
,  and
and  converge strongly to
converge strongly to  .
.
Let  , and let
, and let  for all
for all  . Then
. Then  . By Theorems 3.1 and 3.2, we obtain the following results.
. By Theorems 3.1 and 3.2, we obtain the following results.
Theorem 4.7.
Let  be a nonempty-closed convex subset of a real Hilbert space
be a nonempty-closed convex subset of a real Hilbert space  . Let
. Let  be an integer. For each
be an integer. For each  , let
, let  be an
be an  -strict pseudocontraction for some
-strict pseudocontraction for some  such that
such that  . Assume for each
. Assume for each  ,
,  is a finite sequence of positive numbers such that
is a finite sequence of positive numbers such that  for all
for all  and
and  for all
for all  . Let
. Let  . Let
. Let  be a contraction of
be a contraction of  into itself, and let
into itself, and let  and
and  be sequences generated by
be sequences generated by

for every  , where
, where  and
and  are sequences of numbers satisfying the conditions (C1)–(C3) and (C5). Then,
are sequences of numbers satisfying the conditions (C1)–(C3) and (C5). Then,  and
and  converge strongly to
converge strongly to  .
.
Theorem 4.8.
Let  be a nonempty-closed convex subset of a real Hilbert space
be a nonempty-closed convex subset of a real Hilbert space  . Let
. Let  be an integer. For each
be an integer. For each  , let
, let  be an
be an  -strict pseudocontraction for some
-strict pseudocontraction for some  such that
such that  . Assume for each
. Assume for each  ,
,  is a finite sequence of positive numbers such that
is a finite sequence of positive numbers such that  for all
for all  and
and  for all
for all  . Let
. Let  . Let
. Let  be an arbitrary point in
be an arbitrary point in  and let
and let  and
and  be sequences generated by
be sequences generated by

for every  , where
, where  and
and  are sequences of numbers satisfying the conditions (C1)–(C3) and (C5). Then,
are sequences of numbers satisfying the conditions (C1)–(C3) and (C5). Then,  and
and  converge strongly to
converge strongly to  .
.
Remark 4.9.
-
(1)
Since the nonexpansive mappings have been replaced by the strict pseudocontractions, Theorems 3.1, 3.2, 4.1 and 4.2 extend and improve [6, Theorem 3.1], [8, Theorem 3.5], [9, Theorems 4.1 and 4.2], [18, Theorem 4.1], and the main results in [9–11, 13–16].
-
(2)
Since the weak convergence has been replaced by strong convergence, Theorems 3.1, 3.2, 4.1−4.4 extend and improve [12, Theorem 3.1], [10, Corollary 4.1].
-
(3)
Theorems 4.7 and 4.8 are strong convergence theorems for strict pseudocontractions without
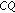 constraints and hence they improve the corresponding results in [19, 21]. Theorems 3.1 and 3.2 also improve [10, Corollary 3.1].
constraints and hence they improve the corresponding results in [19, 21]. Theorems 3.1 and 3.2 also improve [10, Corollary 3.1].
References
Flores-Bazán F: Existence theorems for generalized noncoercive equilibrium problems: the quasi-convex case. SIAM Journal on Optimization 2000,11(3):675–690.
Bigi G, Castellani M, Kassay G: A dual view of equilibrium problems. Journal of Mathematical Analysis and Applications 2008,342(1):17–26. 10.1016/j.jmaa.2007.11.034
Iusem AN, Sosa W: Iterative algorithms for equilibrium problems. Optimization 2003,52(3):301–316. 10.1080/0233193031000120039
Flåm SD, Antipin AS: Equilibrium programming using proximal-like algorithms. Mathematical Programming 1997,78(1):29–41.
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994,63(1–4):123–145.
Ceng L-C, Yao J-C: A hybrid iterative scheme for mixed equilibrium problems and fixed point problems. Journal of Computational and Applied Mathematics 2008,214(1):186–201. 10.1016/j.cam.2007.02.022
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
Yao Y, Liou Y-C, Yao J-C: A new hybrid iterative algorithm for fixed-point problems, variational inequality problems, and mixed equilibrium problems. Fixed Point Theory and Applications 2008, 2008:-15.
Peng J-W, Yao J-C: A new hybrid-extragradient method for generalized mixed equilibrium problems, fixed point problems and variational inequality problems. Taiwanese Journal of Mathematics 2008,12(6):1401–1432.
Peng J-W, Yao J-C: Some new iterative algorithms for generalized mixed equilibrium problems with strict pseudo-contractions and monotone mappings. to appear in Taiwanese Journal of Mathematics
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. Journal of Nonlinear and Convex Analysis 2005,6(1):117–136.
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,331(1):506–515. 10.1016/j.jmaa.2006.08.036
Su Y, Shang M, Qin X: An iterative method of solution for equilibrium and optimization problems. Nonlinear Analysis: Theory, Methods & Applications 2008,69(8):2709–2719. 10.1016/j.na.2007.08.045
Tada A, Takahashi W: Weak and strong convergence theorems for a nonexpansive mapping and an equilibrium problem. Journal of Optimization Theory and Applications 2007,133(3):359–370. 10.1007/s10957-007-9187-z
Ceng L-C, AI-Homidan S, Ansari QH, Yao J-C: An iterative scheme for equilibrium problems and fixed point problems of strict pseudo-contraction mappings. Journal of Computational and Applied Mathematics 2009,223(2):967–974. 10.1016/j.cam.2008.03.032
Chang SS, Joseph Lee HW, Chan CK: A new method for solving equilibrium problem, fixed point problem and variational inequality problem with application to optimization. Nonlinear Analysis: Theory, Methods & Applications. In press
Colao V, Marino G, Xu H-K: An iterative method for finding common solutions of equilibrium and fixed point problems. Journal of Mathematical Analysis and Applications 2008,344(1):340–352. 10.1016/j.jmaa.2008.02.041
Takahashi S, Takahashi W: Strong convergence theorem for a generalized equilibrium problem and a nonexpansive mapping in a Hilbert space. Nonlinear Analysis: Theory, Methods & Applications 2008,69(3):1025–1033. 10.1016/j.na.2008.02.042
Marino G, Xu H-K: Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,329(1):336–346. 10.1016/j.jmaa.2006.06.055
Zhou H: Convergence theorems of fixed points for -strict pseudo-contractions in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,69(2):456–462. 10.1016/j.na.2007.05.032
Acedo GL, Xu H-K: Iterative methods for strict pseudo-contractions in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 2007,67(7):2258–2271. 10.1016/j.na.2006.08.036
Fan K: A generalization of Tychonoff's fixed point theorem. Mathematische Annalen 1961, 142: 305–310. 10.1007/BF01353421
Goebel K, Reich S: Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings, Monographs and Textbooks in Pure and Applied Mathematics. Volume 83. Marcel Dekker, New York, NY, USA; 1984:ix+170.
Xu H-K: Iterative algorithms for nonlinear operators. Journal of the London Mathematical Society. Second Series 2002,66(1):240–256. 10.1112/S0024610702003332
Xu HK: An iterative approach to quadratic optimization. Journal of Optimization Theory and Applications 2003,116(3):659–678. 10.1023/A:1023073621589
Marino G, Colao V, Qin X, Kang SM: Strong convergence of the modified Mann iterative method for strict pseudo-contractions. Computers & Mathematics with Applications 2009,57(3):455–465. 10.1016/j.camwa.2008.10.073
Suzuki T: Strong convergence theorems for infinite families of nonexpansive mappings in general Banach spaces. Fixed Point Theory and Applications 2005,2005(1):103–123. 10.1155/FPTA.2005.103
Acknowledgments
The first author was supported by the National Natural Science Foundation of China (Grants No. 10771228 and No. 10831009), the Science and Technology Research Project of Chinese Ministry of Education (Grant no. 206123), the Education Committee project Research Foundation of Chongqing Normal University (Grant no. KJ070816); the second and third authors were partially supported by the Grants NSC97-2221-E-230-017 and NSC96-2628-E-110-014-MY3, respectively.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Peng, JW., Liou, YC. & Yao, JC. An Iterative Algorithm Combining Viscosity Method with Parallel Method for a Generalized Equilibrium Problem and Strict Pseudocontractions. Fixed Point Theory Appl 2009, 794178 (2009). https://doi.org/10.1155/2009/794178
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/794178
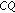 constraints and hence they improve the corresponding results in [
constraints and hence they improve the corresponding results in [