- Research Article
- Open access
- Published:
On a Suzuki Type General Fixed Point Theorem with Applications
Fixed Point Theory and Applications volume 2010, Article number: 234717 (2010)
Abstract
The main result of this paper is a fixed-point theorem which extends numerous fixed point theorems for contractions on metric spaces and recently developed Suzuki type contractions. Applications to certain functional equations and variational inequalities are also discussed.
1. Introduction
The classical Banach contraction theorem has numerous generalizations, extensions, and applications. In a comprehensive comparison of contractive conditions, Rhoades [1] recognized that Ćirić's quasicontraction [2] (see condition (C) below) is the most general condition for a self-map  of a metric space which ensures the existence of a unique fixed point. Pal and Maiti [3] proposed a set of conditions (see (PM.1)–(PM.4) below) as an extension of the principle of quasicontraction (C), under which
of a metric space which ensures the existence of a unique fixed point. Pal and Maiti [3] proposed a set of conditions (see (PM.1)–(PM.4) below) as an extension of the principle of quasicontraction (C), under which  may have more than one fixed point (see Example 2.7 below). Thus the condition (C) is independent of the conditions (PM.1)–(PM.4) (see also Rhoades [4, page 42]).
may have more than one fixed point (see Example 2.7 below). Thus the condition (C) is independent of the conditions (PM.1)–(PM.4) (see also Rhoades [4, page 42]).
On the other hand, Suzuki [5] recently obtained a remarkable generalization of the Banach contraction theorem which itself has been extended and generalized on various settings (see, e.g, [6–15]). With a view of extending Suzuki's contraction theorem [5] and its several generalizations, we combine the ideas of Pal and Maiti [3], Suzuki [5], and Popescu [10] to obtain a very general fixed-point theorem. Subsequently, we use our results to solve certain functional equations and variational inequalities under different conditions than those considered in Bhakta and Mitra [16], Baskaran and Subrahmanyam [17], Pathak et al. [18, 19], Singh and Mishra [11, 12], and Pathak et al. [20, and references thereof].
Consider the following conditions for a map  from a metric space
from a metric space  to itself for
to itself for  :
:
(C) ,
,  ,
,
(PM.1) ,
,  ,
,
(PM.2) ,
,  ,
,
(PM.3) ,
,  ,
,
(PM.4) ,
,  .
.
2. Main Results
Throughout this paper, we denote by  the set of natural numbers. We suppose that
the set of natural numbers. We suppose that

where  , and
, and  are as in conditions (PM.1)–(PM.4).
are as in conditions (PM.1)–(PM.4).
Notice that

Evidently,  .
.
An orbit  of
of  at
at  is a sequence
is a sequence  . A space
. A space  is
is  -orbitally complete if and only if every Cauchy sequence contained in the orbit
-orbitally complete if and only if every Cauchy sequence contained in the orbit  converges in
converges in  , for all
, for all  .
.
An orbit of a multivalued map  , the collection of nonempty subsets of
, the collection of nonempty subsets of  , at
, at  is a sequence
is a sequence  .
.  is called
is called  -orbitally complete if every Cauchy sequence of the form
-orbitally complete if every Cauchy sequence of the form  converges in
converges in  , for all
, for all  . For details, refer to Ćirić [2, 21].
. For details, refer to Ćirić [2, 21].
The following theorem is our main result.
Theorem 2.1.
Let  be a self-map of a metric space
be a self-map of a metric space  and
and  be
be  -orbitally complete. Assume that there exists an
-orbitally complete. Assume that there exists an  such that for any two elements
such that for any two elements  ,
,

implies that at least one of the conditions (PM.1), (PM.2), (PM.3), and (PM.4) is true. Then, the sequence  converges in
converges in  and
and  is a fixed point of
is a fixed point of  .
.
Proof.
Define a sequence  such that
such that  , where
, where  ,
,  . Since
. Since  for any
for any  , one of the conditions (PM.1)–(PM.4) is true for the pair
, one of the conditions (PM.1)–(PM.4) is true for the pair  . If (PM.1) is true, then
. If (PM.1) is true, then

This yields

Similarly, if (PM.2), (PM.3), and (PM.4) are true, then correspondingly we obtain

Hence, from (2.5)-(2.6),

where

Since  , the sequence
, the sequence  is Cauchy. By the
is Cauchy. By the  -orbital completeness of
-orbital completeness of  , the limit
, the limit  of the sequence
of the sequence  is in
is in  . Moreover, there exists
. Moreover, there exists  such that
such that

for  , where
, where  . Therefore, by conditions (PM.1)–(PM.4), we have one of the following for
. Therefore, by conditions (PM.1)–(PM.4), we have one of the following for  :
:

which yields on making  ,
,

and similarly



that is,

or

and in this case

that is,

Thus, in view of (2.11), (2.12), (2.13), (2.18), and (2.15), one of the following is true for  :
:


Case 1.
Suppose that (2.19) is true. Then, by the assumption, one of (PM.1)–(PM.4) is true, that is,

Taking  in these inequaliteis and making
in these inequaliteis and making  , we see that one of the following is true:
, we see that one of the following is true:

All these possibilities lead to the fact that  .
.
Case 2.
Suppose that (2.20) is true. We show that there exists a subsequence  of
of  such that
such that

Recall that by (2.7),

Suppose that

Then

Since without loss of generality, we may take  , we have
, we have

This is a contradiction. Therefore, either

This implies that either

holds for  . Thus, there exists a subsequence
. Thus, there exists a subsequence  of
of  such that
such that

that is,

Hence, by the assumption, one of the conditions (PM.1)–(PM.4) is satisfied for  and
and  , and making
, and making  , we obtain
, we obtain  .
.
Remark 2.2.
If only the condition (PM.4) is satisfied in Theorem 2.1, then the uniqueness of the fixed-point  follows easily. Hence, we have the following (see also [10, Corollary 2.1]).
follows easily. Hence, we have the following (see also [10, Corollary 2.1]).
Corollary 2.3.
Let  be a self-map of a metric space
be a self-map of a metric space  and
and  be
be  -orbitally complete. Assume that there exists an
-orbitally complete. Assume that there exists an  such that for any two elements
such that for any two elements  ,
,

implies the condition (PM.4). Then  has a unique fixed point.
has a unique fixed point.
Remark 2.4.
Corollary 2.3 generalizes certain theorems from [7, 9–11] and others.
Remark 2.5.
It is clear from the proof of Theorem 2.1 that the best value of  in class (PM.1)–(PM.4) is, respectively,
in class (PM.1)–(PM.4) is, respectively,  ,
,  ,
,  , and
, and  .
.
The following result is close in spirit to several generalizations of the Banach contraction theorem by Edelstein [22], Sehgal [23], Chatterjea [24], Rhoades [1, conditions (20) and (22)], and Suzuki [15, Theorem 3].
Theorem 2.6.
Let  be a self-map of a metric space
be a self-map of a metric space  . Assume that
. Assume that
-
(i)
there exists a point
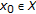 such that the orbit
such that the orbit 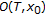 has a cluster point
has a cluster point  ,
,
(ii) and
and  are continuous at
are continuous at  ,
,
-
(iii)
for any two distinct elements

 (2.33)
(2.33)
implies one of the following conditions:
(PM.1)* ,
,
(PM.2)* ,
,
(PM.3)* ,
,
(PM.4)*
Then  is a fixed point of
is a fixed point of  .
.
Proof.
An appropriate blend of the proof of Theorems 2.1 and 2 of Pal and Maiti [3] works.
If only the condition (PM.4)* is satisfied in Theorem 2.6, then the uniqueness of the fixed-point  follows easily.
follows easily.
Example 2.7.
Let  and
and  ,
,  . Then, the map
. Then, the map  satisfies all the requirements of Theorem 2.1 with
satisfies all the requirements of Theorem 2.1 with  ,
,  , and
, and  . Further,
. Further,  is not a Ćirić-Suzuki contraction, that is,
is not a Ćirić-Suzuki contraction, that is,  does not satify the requirements of [10, Corollary 2.1]. Evidently,
does not satify the requirements of [10, Corollary 2.1]. Evidently,  is not a quasicontraction.
is not a quasicontraction.
Example 2.8.
Let  and
and

Then, one of the conditions (PM.1)–(PM.4) is satisfied (e.g.,  ,
,  ). As
). As  has two fixed points, it cannot satisfy any of the conditions which guarantee the existence of a unique fixed point.
has two fixed points, it cannot satisfy any of the conditions which guarantee the existence of a unique fixed point.
Example 2.9.
Let  and
and

Then, the map  satisfies all the requirements of Theorem 2.6. If in Theorem 2.6, the initial choice is
satisfies all the requirements of Theorem 2.6. If in Theorem 2.6, the initial choice is  (resp.,
(resp.,  ), then
), then  converges to 6 (resp., 3).
converges to 6 (resp., 3).
For any subsets  of
of  ,
,  denotes the gap between
denotes the gap between  and
and  , while
, while

As usual, we write  (resp.,
(resp.,  ) for
) for  (resp.,
(resp.,  ) when
) when  .
.
We use Theorem 2.1 to obtain the following result for a multivalued map.
Theorem 2.10.
Let  and let
and let  be
be  -orbitally complete. Assume that there exist
-orbitally complete. Assume that there exist  , and
, and  as defined in Section 2 such that for any
as defined in Section 2 such that for any 

implies that at least one of the following conditions is true:
(PM.1)** ,
,
(PM.2)** ,
,
(PM.3)** ,
,
(PM.4)**
Then  has a fixed point.
has a fixed point.
Proof.
It may be completed following Reich [25], Ćirić [2], and Singh and Mishra [11]. However, a basic skech of the same is given below.
Let  . Define a single-valued map
. Define a single-valued map  as follows. For each
as follows. For each  , let
, let  be a point of
be a point of  such that
such that

Since  ,
,  . So, (2.37) gives
. So, (2.37) gives

and in view of conditions (PM.1)**–(PM.4)**, this implies that one of the following is true:

This means Theorem 2.1 applies as " " in the statement of Theorem 2.1 may be replaced by "
" in the statement of Theorem 2.1 may be replaced by " ". Hence, there exists a point
". Hence, there exists a point  such that
such that  , and
, and  .
.
3. Applications
3.1. Application to Dynamic Programming
In this section, we assume that  and
and  are Banach spaces,
are Banach spaces,  and
and  . Let
. Let  denote the field of reals,
denote the field of reals,  ,
,  and
and  . The subspaces
. The subspaces  and
and  are considered as the state and decision spaces, respectively. Then, the problem of dynamic programming reduces to the problem of solving the functional equation
are considered as the state and decision spaces, respectively. Then, the problem of dynamic programming reduces to the problem of solving the functional equation

In multistage processes, some functional equations arise in a natural way (cf. Bellman [26] and Bellman and Lee [27]). The intent of this section is to study the existence of the solution of the functional equation (3.1) arising in dynamic programming.
Let  denote the set of all bounded real-valued functions on
denote the set of all bounded real-valued functions on  . For an arbitrary
. For an arbitrary  , define
, define  . Then,
. Then,  is a Banach space. Assume that
is a Banach space. Assume that  ,
,  and the following conditions hold:
and the following conditions hold:
(DP.1) are bounded.
are bounded.
(DP.2)Assume that for every  ,
,  and
and  ,
,

implies

where  is defined as follows:
is defined as follows:

Theorem 3.1.
Assume that the conditions (DP.1) and (DP.2) are satisfied. Then, the functional equation (3.1) has a unique bounded solution.
Proof.
We note that  is a complete metric space, where
is a complete metric space, where  is the metric induced by the supremum norm on
is the metric induced by the supremum norm on  . By (DP.1),
. By (DP.1),  is a self-map of
is a self-map of  .
.
Pick  and
and  . Let μ be an arbitrary positive number. We can choose
. Let μ be an arbitrary positive number. We can choose  such that
such that

where  ,
,  .
.
Further, we have


Therefore, (3.2) becomes

Set

From (3.5), (3.7), and (3.8), we have

Similarly, from (3.5), (3.6), and (3.8), we get

From (3.10) and (3.11), we have

Since the inequality (3.12) is true for any  , and
, and  is arbitrary, we find from (3.8) that
is arbitrary, we find from (3.8) that

implies

So Corollary 2.3 applies, wherein  corresponds to the map
corresponds to the map  . Therefore,
. Therefore,  has a unique fixed-point
has a unique fixed-point  , that is,
, that is,  is the unique bounded solution of the functional equation (3.1).
is the unique bounded solution of the functional equation (3.1).
3.2. Application to Variational Inequalities
As another application of Corollary 2.3, we show the existence of solutions of variational inequalities as in the work of Belbas and Mayergoyz [28]. Variational inequalities arise in optimal stochastic control [29] as well as in other problems in mathematical physics, for examples, deformation of elastic bodies stretched over solid obstacles, elastoplastic torsion, and so forth, [30]. The iterative method for solutions of discrete variational inequalities is very suitable for implementation on parallel computers with single-instruction, multiple-data architecture, particularly on massively parallel processors.
The variational inequality problem is to find a function  such that
such that

where  is a nonempty
is a nonempty  -starshaped open bounded subset of
-starshaped open bounded subset of  for some
for some  with smooth boundary such that
with smooth boundary such that  ,
,  is an elliptic operator defined on
is an elliptic operator defined on  by
by

where summation with respect to repeated indices is implied,  ,
,  is a strictly positive definite matrix, uniformly in
is a strictly positive definite matrix, uniformly in  , for
, for  and
and  are smooth functions defined in
are smooth functions defined in  and
and  satisfies the condition:
satisfies the condition:  ,
,  .
.
The corresponding problem of stochastic optimal control can be described as follows:  is the generator of a diffusion process in
is the generator of a diffusion process in  ,
,  is a discount factor,
is a discount factor,  is the continuous cost, and
is the continuous cost, and  represents the cost incurred by stopping the process. The boundary condition "
represents the cost incurred by stopping the process. The boundary condition " on
on  " expresses the fact that stopping takes place either prior or at the time that the diffusion process exists from
" expresses the fact that stopping takes place either prior or at the time that the diffusion process exists from  .
.
A problem related to (3.15) is the two-obstacle variational inequality. Given two smooth functions  and μ defined on
and μ defined on  such that
such that  in
in  ,
,  on
on  , the corresponding variational inequality is as follows:
, the corresponding variational inequality is as follows:

Note that the problem (3.17) arises in stochastic game theory.
Let  be an
be an  matrix corresponding to the finite difference discretizations of the operator
matrix corresponding to the finite difference discretizations of the operator  . We make the following assumptions about the matrix
. We make the following assumptions about the matrix  :
:

These assumptions are related to the definition of " -matrices", arising from the finite difference discretization of continuous elliptic operators having the property (3.18) under the appropriate conditions and
-matrices", arising from the finite difference discretization of continuous elliptic operators having the property (3.18) under the appropriate conditions and  denotes the set of all discretized vectors in
denotes the set of all discretized vectors in  (see [31, 32]). Note that the matrix
(see [31, 32]). Note that the matrix  is an
is an  -matrix if and only if every off-diagonal entry of
-matrix if and only if every off-diagonal entry of  is nonpositive.
is nonpositive.
Let  . Then, the corresponding properties for the
. Then, the corresponding properties for the  -matrices are
-matrices are

Let  and
and  an
an  matrix such that
matrix such that  and
and  for
for  . Then, we have
. Then, we have  .
.
Now, we show the existence of iterative solutions of variational inequalities.
Consider the following discrete variational inequalities mentioned above:

where  is an operator from
is an operator from  into itself implicitly defined by
into itself implicitly defined by

for all  such that for all
such that for all  , the condition
, the condition

holds. Suppose that the condition (3.22) implies that  is defined in
is defined in  as in (3.21), then (3.20) is equivalent to the fixed-point problem
as in (3.21), then (3.20) is equivalent to the fixed-point problem

that is,  .
.
Notice that in two-person game, we have to determine the best strategies for each player on the basis of maximin and minimax criterion of optimality. This criterion will be well stated as follows: a player lists his/her worst possible outcomes, and then he/she chooses that strategy which corresponds to the best of these worst outcomes. Here, the problem (3.20) exhibits the situation in which two players are trying to control a diffusion process; the first player is trying to maximize a cost functional, and the second player is trying to minimize a similar functional. The first player is called the maximizing player and the second one the minimizing player. Here,  represents the continuous rate of cost for both players,
represents the continuous rate of cost for both players,  is the stopping cost for the maximizing player, and μ is the stopping cost for the minimizing player. This problem is fixed by inducting an operator
is the stopping cost for the maximizing player, and μ is the stopping cost for the minimizing player. This problem is fixed by inducting an operator  implicitly defined for all
implicitly defined for all  as in (3.21).
as in (3.21).
Theorem 3.2.
Under the assumptions (3.18) and (3.19), a solution for (3.23) exists.
Proof.
Let  for any
for any  and any
and any  . Now, for any
. Now, for any  , since
, since  , we have
, we have

that is, if the maximizing player succeeds to maximize a cost functional in his/her strategy which corresponds to the best of  worst outcomes from his/her list, then the game would be one-sided. In this situation, we introduce the one sided operator
worst outcomes from his/her list, then the game would be one-sided. In this situation, we introduce the one sided operator

Therefore, we have

Now, if  , then since
, then since

by using (3.18), we have

If  , then since
, then since

we have

Hence, from (3.18)–(3.20), we have

Since  and
and  are arbitrarily chosen, we have
are arbitrarily chosen, we have

Therefore, from (3.31) and (3.32), it follows that

This yields

where  . Thus, we see that under the assumptions (3.18) and (3.19), for all
. Thus, we see that under the assumptions (3.18) and (3.19), for all  ,
,

implies

Note that  is complete and
is complete and  a closed subset of
a closed subset of  , it follows that
, it follows that  is complete. As a consequence,
is complete. As a consequence,  is orbitally complete.
is orbitally complete.
Hence, we conclude that all the conditions of Corollary 2.3 are satisfied in  . Therefore, Corollary 2.3 ensures the existence of a solution of (3.23).
. Therefore, Corollary 2.3 ensures the existence of a solution of (3.23).
References
Rhoades BE: A comparison of various definitions of contractive mappings. Transactions of the American Mathematical Society 1977, 226: 257–290.
Ćirić LB: A generalization of Banach's contraction principle. Proceedings of the American Mathematical Society 1974, 45: 267–273.
Pal TK, Maiti M: Extensions of fixed point theorems of Rhoades and Ćirić. Proceedings of the American Mathematical Society 1977,64(2):283–286.
Rhoades BE: Extensions of some fixed point theorems of Ćirić, Maiti, and Pal. Mathematics Seminar Notes. Kobe University 1978,6(1):41–46.
Suzuki T: A generalized Banach contraction principle that characterizes metric completeness. Proceedings of the American Mathematical Society 2008,136(5):1861–1869.
Abkar A, Eslamian M: Fixed point theorems for Suzuki generalized nonexpansive multivalued mappings in Banach spaces. Fixed Point Theory and Applications 2010, 2010:-10.
Dhompongsa S, Yingtaweesittikul H: Fixed points for multivalued mappings and the metric completeness. Fixed Point Theory and Applications 2009, 2009:-15.
Kikkawa M, Suzuki T: Three fixed point theorems for generalized contractions with constants in complete metric spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,69(9):2942–2949. 10.1016/j.na.2007.08.064
Moţ G, Petruşel A: Fixed point theory for a new type of contractive multivalued operators. Nonlinear Analysis: Theory, Methods & Applications 2009,70(9):3371–3377. 10.1016/j.na.2008.05.005
Popescu O: Two fixed point theorems for generalized contractions with constants in complete metric space. Central European Journal of Mathematics 2009,7(3):529–538. 10.2478/s11533-009-0019-2
Singh SL, Mishra SN: Coincidence theorems for certain classes of hybrid contractions. Fixed Point Theory and Applications 2010, 2010:-14.
Singh SL, Mishra SN: Remarks on recent fixed point theorems. Fixed Point Theory and Applications 2010, 2010:-18.
Suzuki T: Some remarks on recent generalization of the Banach contraction principle. Proceedings of the 8th International Conference on Fixed Point Theory and Its Applications, 2007 751–761.
Suzuki T: Fixed point theorems and convergence theorems for some generalized nonexpansive mappings. Journal of Mathematical Analysis and Applications 2008,340(2):1088–1095. 10.1016/j.jmaa.2007.09.023
Suzuki T: A new type of fixed point theorem in metric spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(11):5313–5317. 10.1016/j.na.2009.04.017
Bhakta PC, Mitra S: Some existence theorems for functional equations arising in dynamic programming. Journal of Mathematical Analysis and Applications 1984,98(2):348–362. 10.1016/0022-247X(84)90254-3
Baskaran R, Subrahmanyam PV: A note on the solution of a class of functional equations. Applicable Analysis 1986,22(3–4):235–241. 10.1080/00036818608839621
Pathak HK, Cho YJ, Kang SM, Lee BS: Fixed point theorems for compatible mappings of type (P) and applications to dynamic programming. Le Matematiche 1995,50(1):15–33.
Pathak HK, Fisher B: Common fixed point theorems with applications in dynamic programming. Glasnik Matematički 1996,31(51)(2):321–328.
Pathak HK, Mishra SN, Kalinde AK: Some Gregus type common fixed point theorems with applications. Demonstratio Mathematica 2003,36(2):413–426.
Ćirić LB: Generalized contractions and fixed-point theorems. Publications de l'Institut Mathématique 1971, 12(26): 19–26.
Edelstein M: On fixed and periodic points under contractive mappings. Journal of the London Mathematical Society 1962, 37: 74–79. 10.1112/jlms/s1-37.1.74
Sehgal VM: On fixed and periodic points for a class of mappings. Journal of the London Mathematical Society 1972, 5: 571–576. 10.1112/jlms/s2-5.3.571
Chatterjea SK: Fixed-point theorems. Comptes Rendus de l'Académie Bulgare des Sciences 1972, 25: 727–730.
Reich S: Fixed points of contractive functions. Bollettino della Unione Matematica Italiana 1972, 5: 26–42.
Bellman R: Methods of Nonliner Analysis. Vol. II, Mathematics in Science and Engineering, Vol. 61-II. Academic Press, New York, NY, USA; 1973:xvii+261.
Bellman R, Lee ES: Functional equations in dynamic programming. Aequationes Mathematicae 1978,17(1):1–18. 10.1007/BF01818535
Belbas SA, Mayergoyz ID: Applications of fixed-point methods to discrete variational and quasivariational inequalities. Numerische Mathematik 1987,51(6):631–654. 10.1007/BF01400174
Bensoussan A, Lions J-L: Applications des inéquations variationnelles en contrôle stochastique, Méthodes Mathématiques de l'Informatique, no. 6. Dunod, Paris, France; 1978:viii+545.
Duvaut G, Lions J-L: Inequalities in Mechanics and Physics, Grundlehren der Mathematischen Wissenschaften, 21. Springer, Berlin, Germany; 1976:xvi+397.
Berman A, Plemmons RJ: Nonnegative Matrices in the Mathematical Sciences, Computer Science and Applied Mathematics. Academic Press, New York, NY, USA; 1979:xviii+316.
Varga RS: Matrix Iterative Analysis. Prentice-Hall, Englewood Cliffs, NJ, USA; 1982.
Acknowledgment
This research is supported by the Directorate of Research Development, Walter Sisulu University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Singh, S., Pathak, H. & Mishra, S. On a Suzuki Type General Fixed Point Theorem with Applications. Fixed Point Theory Appl 2010, 234717 (2010). https://doi.org/10.1155/2010/234717
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/234717
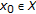 such that the orbit
such that the orbit 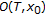 has a cluster point
has a cluster point  ,
,
