- Research Article
- Open access
- Published:
Fixed Point Theorems on Spaces Endowed with Vector-Valued Metrics
Fixed Point Theory and Applications volume 2010, Article number: 281381 (2010)
Abstract
The purpose of this work is to present some (local and global) fixed point results for singlevalued and multivalued generalized contractions on spaces endowed with vector-valued metrics. The results are extensions of some theorems given by Perov (1964), Bucur et al. (2009), M. Berinde and V. Berinde (2007), O'Regan et al. (2007), and so forth.
1. Introduction
The classical Banach contraction principle was extended for contraction mappings on spaces endowed with vector-valued metrics by Perov in 1964 (see [1]).
Let  be a nonempty set. A mapping
be a nonempty set. A mapping  is called a vector-valued metric on
is called a vector-valued metric on  if the following properties are satisfied:
if the following properties are satisfied:
 for all
for all  ; if
; if  , then
, then  ;
;
 for all
for all  ;
;
 for all
for all  .
.
If  ,
,  ,
,  , and
, and  , by
, by  (resp.,
(resp.,  ) we mean that
) we mean that  (resp.,
(resp.,  ) for
) for  and by
and by  we mean that
we mean that  for
for  .
.
A set  equipped with a vector-valued metric
equipped with a vector-valued metric  is called a generalized metric space. We will denote such a space with
is called a generalized metric space. We will denote such a space with  . For the generalized metric spaces, the notions of convergent sequence, Cauchy sequence, completeness, open subset, and closed subset are similar to those for usual metric spaces.
. For the generalized metric spaces, the notions of convergent sequence, Cauchy sequence, completeness, open subset, and closed subset are similar to those for usual metric spaces.
If  is a generalized metric space,
is a generalized metric space,  and
and  , with
, with  for each
for each  , then we will denote by
, then we will denote by

the open ball centered in  with radius
with radius  , by
, by  the closure (in
the closure (in  ) of the open ball, and by
) of the open ball, and by

the closed ball centered in  with radius
with radius 
If  is a singlevalued operator, then we denote by
is a singlevalued operator, then we denote by  the set of all fixed points of
the set of all fixed points of  ; that is,
; that is, 
For the multivalued operators we use the following notations:

Now, if  is a multivalued operator, then we denote by
is a multivalued operator, then we denote by  the fixed points set of
the fixed points set of  , that is,
, that is,  .
.
The set  is called the graph of the multivalued operator
is called the graph of the multivalued operator  .
.
In the context of a metric space  , if
, if  , then we will use the following notations:
, then we will use the following notations:
(a)the gap functional  :
:

(b)the generalized excess functional  :
:

(c)the generalized Pompeiu-Hausdorff functional  :
:

It is well known that  is a generalized metric, in the sense that if
is a generalized metric, in the sense that if  , then
, then  .
.
Throughout this paper we denote by  the set of all
the set of all  matrices with positive elements, by
matrices with positive elements, by  the zero
the zero  matrix, and by
matrix, and by  the identity
the identity  matrix. If
matrix. If  , then the symbol
, then the symbol  stands for the transpose matrix of
stands for the transpose matrix of  . Notice also that, for the sake of simplicity, we will make an identification between row and column vectors in
. Notice also that, for the sake of simplicity, we will make an identification between row and column vectors in  .
.
Recall that a matrix  is said to be convergent to zero if and only if
is said to be convergent to zero if and only if  as
as  (see Varga [2]).
(see Varga [2]).
Notice that, for the proof of the main results, we need the following theorem, part of which being a classical result in matrix analysis; see, for example, [3, Lemma  , page 55], [4, page 37], and [2, page 12]. For the assertion (iv) see [5].
, page 55], [4, page 37], and [2, page 12]. For the assertion (iv) see [5].
Theorem 1.1.
Let  . The following are equivalents.
. The following are equivalents.
(i) is convergent towards zero.
is convergent towards zero.
(ii) as
as  .
.
(iii)The eigenvalues of  are in the open unit disc, that is,
are in the open unit disc, that is,  , for every
, for every  with
with  .
.
(iv)The matrix  is nonsingular and
is nonsingular and

(v)The matrix  is nonsingular and
is nonsingular and  has nonnenegative elements.
has nonnenegative elements.
(vi) and
and  as
as  , for each
, for each  .
.
Remark 1.2.
Some examples of matrix convergent to zero are
(a)any matrix  , where
, where  and
and  ;
;
(b)any matrix  , where
, where  and
and  ;
;
(c)any matrix  , where
, where  and
and  .
.
For other examples and considerations on matrices which converge to zero, see Rus [4], Turinici [6], and so forth.
Main result for self contractions on generalized metric spaces is Perov's fixed point theorem; see [1].
Theorem 1.3 (Perov [3]).
Let  be a complete generalized metric space and the mapping
be a complete generalized metric space and the mapping  with the property that there exists a matrix
with the property that there exists a matrix  such that
such that  for all
for all  .
.
If  is a matrix convergent towards zero, then
is a matrix convergent towards zero, then
(1) ;
;
(2)the sequence of successive approximations  ,
,  is convergent and it has the limit
is convergent and it has the limit  , for all
, for all  ;
;
(3)one has the following estimation:

(4)if  satisfies the condition
satisfies the condition  , for all
, for all  and considering the sequence
and considering the sequence  one has
one has

On the other hand, notice that the evolution of macrosystems under uncertainty or lack of precision, from control theory, biology, economics, artificial intelligence, or other fields of knowledge, is often modeled by semilinear inclusion systems:

(where  for
for  are multivalued operators; here
are multivalued operators; here  stands for the family of all nonempty subsets of a Banach space
stands for the family of all nonempty subsets of a Banach space  ). The system above can be represented as a fixed point problem of the form
). The system above can be represented as a fixed point problem of the form

Hence, it is of great interest to give fixed point results for multivalued operators on a set endowed with vector-valued metrics or norms. However, some advantages of a vector-valued norm with respect to the usual scalar norms were already pointed out by Precup in [5]. The purpose of this work is to present some new fixed point results for generalized (singlevalued and multivalued) contractions on spaces endowed with vector-valued metrics. The results are extensions of the theorems given by Perov [1], O'Regan et al. [7], M. Berinde and V. Berinde [8], and by Bucur et al. [9].
2. Main Results
We start our considerations by a local fixed point theorem for a class of generalized singlevalued contractions.
Theorem 2.1.
Let  be a complete generalized metric space,
be a complete generalized metric space,  ,
,  with
with  for each
for each  and let
and let  having the property that there exist
having the property that there exist  such that
such that

for all  . We suppose that
. We suppose that
(1) is a matrix that converges toward zero;
is a matrix that converges toward zero;
(2)if  is such that
is such that  , then
, then  ;
;
(3)
Then 
In addition, if the matrix  converges to zero, then
converges to zero, then  .
.
Proof.
We consider  the sequence of successive approximations for the mapping
the sequence of successive approximations for the mapping  , defined by
, defined by

Using  , we have
, we have  .
.
Thus, by  we get that
we get that  and hence
and hence  . Similarly,
. Similarly,  .
.
Since  , by
, by  we get
we get

Thus  and hence
and hence  .
.
Inductively, we construct the sequence  in
in  satisfying, for all
satisfying, for all  , the following conditions:
, the following conditions:
(i) ;
;
(ii) ;
;
(iii) .
.
From  we get, for all
we get, for all  and
and  , that
, that

Hence  is a Cauchy sequence. Using the fact that
is a Cauchy sequence. Using the fact that  is a complete metric space, we get that
is a complete metric space, we get that  is convergent in the closed set
is convergent in the closed set  . Thus, there exists
. Thus, there exists  such that
such that 
Next, we show that 
Indeed, we have the following estimation:

Hence  . In addition, letting
. In addition, letting  in the estimation of
in the estimation of  , we get
, we get

We show now the uniqueness of the fixed point.
Let  with
with  . Then
. Then

which implies  Taking into account that
Taking into account that  is nonsingular and
is nonsingular and  we deduce that
we deduce that  and thus
and thus 
Remark 2.2.
By similitude to [10], a mapping  satisfying the condition
satisfying the condition

for some matrices  with
with  a matrix that converges toward zero, could be called an almost contraction of Perov type.
a matrix that converges toward zero, could be called an almost contraction of Perov type.
We have also a global version of Theorem 2.1, expressed by the following result.
Corollary 2.3.
Let  be a complete generalized metric space. Let
be a complete generalized metric space. Let  be a mapping having the property that there exist
be a mapping having the property that there exist  such that
such that

If  is a matrix that converges towards zero, then
is a matrix that converges towards zero, then
(1) ;
;
(2)the sequence  given by
given by  converges towards a fixed point of
converges towards a fixed point of  , for all
, for all  ;
;
(3)one has the estimation

where 
In addition, if the matrix  converges to zero, then
converges to zero, then 
Remark 2.4.
Any matrix  , where
, where  and
and  , satisfies the assumptions (
, satisfies the assumptions ( )-(
)-( ) in Theorem 2.1.
) in Theorem 2.1.
Remark 2.5.
Let us notice here that some advantages of a vector-valued norm with respect to the usual scalar norms were very nice pointed out, by several examples, in Precup in [5]. More precisely, one can show that, in general, the condition that  is a matrix convergent to zero is weaker than the contraction conditions for operators given in terms of the scalar norms on
is a matrix convergent to zero is weaker than the contraction conditions for operators given in terms of the scalar norms on  of the following type:
of the following type:

 or
or
 .
.
As an application of the previous results we present an existence theorem for a system of operatorial equations.
Theorem 2.6.
Let  be a Banach space and let
be a Banach space and let  be two operators. Suppose that there exist
be two operators. Suppose that there exist  ,
,  such that, for each
such that, for each  , one has:
, one has:
(1)
(2)
In addition, assume that the matrix  converges to
converges to  .
.
Then, the system

has at least one solution  . Moreover, if, in addition, the matrix
. Moreover, if, in addition, the matrix  converges to zero, then the above solution is unique.
converges to zero, then the above solution is unique.
Proof.
Consider  and the operator
and the operator  given by the expression
given by the expression  . Then our system is now represented as a fixed point equation of the following form:
. Then our system is now represented as a fixed point equation of the following form:  ,
,  . Notice also that the conditions
. Notice also that the conditions  can be jointly represented as follows:
can be jointly represented as follows:

Hence, Corollary 2.3 applies in  , with
, with  .
.
We present another result in the case of a generalized metric space but endowed with two metrics.
Theorem 2.7.
Let  be a nonempty set and let
be a nonempty set and let  be two generalized metrics on
be two generalized metrics on  . Let
. Let  be an operator. We assume that
be an operator. We assume that
(1)there exists  such that
such that 
(2) is a complete generalized metric space;
is a complete generalized metric space;
(3) is continuous;
is continuous;
(4)there exists  such that for all
such that for all  one has
one has

If the matrix  converges towards zero, then
converges towards zero, then 
In addition, if the matrix  converges to zero, then
converges to zero, then 
Proof.
We consider the sequence of successive approximations  defined recurrently by
defined recurrently by  ,
,  being arbitrary. The following statements hold:
being arbitrary. The following statements hold:

Now, let  ,
,  . We estimate
. We estimate

Letting  we obtain that
we obtain that  . Thus
. Thus  is a Cauchy sequence with respect to
is a Cauchy sequence with respect to  .
.
On the other hand, using the statement  , we get
, we get

Hence,  is a Cauchy sequence with respect to
is a Cauchy sequence with respect to  . Since
. Since  is complete, one obtains the existence of an element
is complete, one obtains the existence of an element  such that
such that  with respect to
with respect to  .
.
We prove next that  , that is,
, that is,  . Indeed, since
. Indeed, since  , for all
, for all  , letting
, letting  and taking into account that
and taking into account that  is continuous with respect to
is continuous with respect to  , we get that
, we get that  .
.
The uniqueness of the fixed point  is proved below.
is proved below.
Let  such that
such that  . We estimate
. We estimate

Thus, using the additional assumption on the matrix  , we have that
, we have that

In what follows, we will present some results for the case of multivalued operators.
Theorem 2.8.
Let  be a complete generalized metric space and let
be a complete generalized metric space and let  ,
,  with
with  for each
for each  . Consider
. Consider  a multivalued operator. One assumes that
a multivalued operator. One assumes that
(i)there exist  such that for all
such that for all  and
and  there exists
there exists  with
with

(ii)there exists  such that
such that 
(iii)if  is such that
is such that  , then
, then  .
.
If  is a matrix convergent towards zero, then
is a matrix convergent towards zero, then  .
.
Proof.
By  and
and  , there exists
, there exists  such that
such that

For  , there exists
, there exists  with
with

Hence

Next, for  , there exists
, there exists  with
with

and hence

By induction, we construct the sequence  in
in  such that, for all
such that, for all  , we have
, we have
(1)
(2)
(3) .
.
By a similar approach as before (see the proof of Theorem 2.1), we get that  is a Cauchy sequence in the complete space
is a Cauchy sequence in the complete space  . Hence
. Hence  is convergent in
is convergent in  . Thus, there exists
. Thus, there exists  such that
such that 
Next we show that  .
.
Using  and the fact that
and the fact that  , for all
, for all  , we get, for each
, we get, for each  , the existence of
, the existence of  such that
such that

On the other hand

Letting  , we get
, we get  Hence, we have
Hence, we have  and since
and since  and
and  is closed set, we get that
is closed set, we get that  .
.
Remark 2.9.
From the proof of the above theorem, we also get the following estimation:

where  is a fixed point for the multivalued operator
is a fixed point for the multivalued operator  , and the pair
, and the pair  is arbitrary.
is arbitrary.
We have also a global variant for the Theorem 2.8 as follows.
Corollary 2.10.
Let  be a complete generalized metric space and
be a complete generalized metric space and  a multivalued operator. One supposes that there exist
a multivalued operator. One supposes that there exist  such that for each
such that for each  and all
and all  , there exists
, there exists  with
with

If  is a matrix convergent towards zero, then
is a matrix convergent towards zero, then  .
.
Remark 2.11.
By a similar approach to that given in Theorem 2.6, one can obtain an existence result for a system of operatorial inclusions of the following form:

where  are multivalued operators satisfying a contractive type condition (see also [9]).
are multivalued operators satisfying a contractive type condition (see also [9]).
The following results are obtained in the case of a set  endowed with two metrics.
endowed with two metrics.
Theorem 2.12.
Let  be a complete generalized metric space and
be a complete generalized metric space and  another generalized metric on
another generalized metric on  . Let
. Let  be a multivalued operator. One assumes that
be a multivalued operator. One assumes that
(i)there exists a matrix  such that
such that  , for all
, for all  ;
;
(ii) has closed graph;
has closed graph;
(iii)there exist  such that for all
such that for all  and
and  , there exists
, there exists  with
with

If  is a matrix convergent towards zero, then
is a matrix convergent towards zero, then  .
.
Proof.
Let  such that
such that  .
.
For  , there exists
, there exists  such that
such that

For  , there exists
, there exists  such that
such that

Consequently, we construct by induction the sequence  in
in  which satisfies the following properties:
which satisfies the following properties:
(1) , for all
, for all  ;
;
(2) , for all
, for all  .
.
We show that  is a Cauchy sequence in
is a Cauchy sequence in  with respect to
with respect to  . In order to do that, let
. In order to do that, let  . One has the estimation
. One has the estimation

Since the matrix  converges towards zero, one has
converges towards zero, one has  as
as  . Letting
. Letting  one get
one get  which implies that
which implies that  is a Cauchy sequence with respect to
is a Cauchy sequence with respect to  .
.
Using  , we obtain that
, we obtain that  as
as  . Thus,
. Thus,  is a Cauchy sequence with respect to
is a Cauchy sequence with respect to  too.
too.
Since  is complete, the sequence
is complete, the sequence  is convergent in
is convergent in  . Thus there exists
. Thus there exists  such that
such that  with respect to
with respect to  .
.
Finally, we show that  .
.
Since  , for all
, for all  and
and  has closed graph, by using the limit presented above, we get that
has closed graph, by using the limit presented above, we get that  , that is,
, that is,  .
.
Remark 2.13.
-
(1)
Theorem 2.12 holds even if the assumption
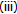 is replaced by
is replaced by
 there exist
there exist  such that for all
such that for all  and
and  , there exists
, there exists  such that
such that
-
(2)
Letting
 in the estimation of
in the estimation of 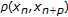 , presented in the proof of Theorem 2.12, we get
, presented in the proof of Theorem 2.12, we get  (2.34)
(2.34)
Using the relation between the generalized metrics  and
and  , one has immediately
, one has immediately

Theorem 2.14.
Let  be a complete generalized metric space and
be a complete generalized metric space and  another generalized metric on
another generalized metric on  . Let
. Let  ,
,  with
with  for each
for each  and let
and let  be a multivalued operator. Suppose that
be a multivalued operator. Suppose that
(i)there exists  such that
such that  , for all
, for all  ;
;
(ii) has closed graph;
has closed graph;
(iii)there exist  such that
such that  is a matrix that converges to zero and for all
is a matrix that converges to zero and for all  and
and  , there exists
, there exists  such that
such that

(iv)if  is such that
is such that  , then
, then  ;
;
(v)
Then  .
.
Proof.
Let  such that
such that  . By
. By  one has
one has

which implies  .
.
Since  , there exists
, there exists  such that
such that

Hence,

which implies that  , that is,
, that is,  .
.
For  , there exists
, there exists  such that
such that

Then the following estimation holds:

and thus  , that is,
, that is,  .
.
Inductively, we can construct the sequence  which has its elements in the closed ball
which has its elements in the closed ball  and satisfies the following conditions:
and satisfies the following conditions:
(1) , for all
, for all  ;
;
(2) , for all
, for all  .
.
By a similar approach as in the proof of Theorem 2.12, the conclusion follows.
A homotopy result for multivalued operators on a set endowed with a vector-valued metric is the following.
Theorem 2.15.
Let  be a generalized complete metric space in Perov sense, let
be a generalized complete metric space in Perov sense, let  be an open subset of
be an open subset of  , and let
, and let  be a closed subset of
be a closed subset of  , with
, with  . Let
. Let  be a multivalued operator with closed (with respect to
be a multivalued operator with closed (with respect to  ) graph, such that the following conditions are satisfied:
) graph, such that the following conditions are satisfied:
(a) , for each
, for each  and each
and each  ;
;
(b)there exist  such that the matrix
such that the matrix  is convergent to zero such that for each
is convergent to zero such that for each  , for each
, for each  and all
and all  , there exists
, there exists  with
with  .
.
(c)there exists a continuous increasing function  such that for all
such that for all  , each
, each  and each
and each  there exists
there exists  such that
such that  ;
;
(d)if  are such that
are such that  , then
, then  ;
;
Then  has a fixed point if and only if
has a fixed point if and only if  has a fixed point.
has a fixed point.
Proof.
Suppose that  has a fixed point
has a fixed point  . From (a) we have that
. From (a) we have that  . Define
. Define

Clearly  , since
, since  . Consider on
. Consider on  a partial order defined as follows:
a partial order defined as follows:

Let  be a totally ordered subset of
be a totally ordered subset of  and consider
and consider  . Consider a sequence
. Consider a sequence  such that
such that  for each
for each  and
and  , as
, as  . Then
. Then

When  , we obtain
, we obtain  and, thus,
and, thus,  is
is  -Cauchy. Thus
-Cauchy. Thus  is convergent in
is convergent in  . Denote by
. Denote by  its limit. Since
its limit. Since  and since
and since  is
is  -closed, we have that
-closed, we have that  . Thus, from (a), we have
. Thus, from (a), we have  . Hence
. Hence  . Since
. Since  is totally ordered we get that
is totally ordered we get that  , for each
, for each  . Thus
. Thus  is an upper bound of
is an upper bound of  . By Zorn's Lemma,
. By Zorn's Lemma,  admits a maximal element
admits a maximal element  . We claim that
. We claim that  . This will finish the proof.
. This will finish the proof.
Suppose  . Choose
. Choose  with
with  for each
for each  and
and  such that
such that  , where
, where  . Since
. Since  , by (c), there exists
, by (c), there exists  such that
such that  . Thus,
. Thus,  .
.
Since  , the multivalued operator
, the multivalued operator  satisfies, for all
satisfies, for all  , the assumptions of Theorem 2.1 Hence, for all
, the assumptions of Theorem 2.1 Hence, for all  , there exists
, there exists  such that
such that  . Thus
. Thus  . Since
. Since  , we immediately get that
, we immediately get that  . This is a contradiction with the maximality of
. This is a contradiction with the maximality of  .
.
Conversely, if  has a fixed point, then putting
has a fixed point, then putting  and using first part of the proof we get the conclusion.
and using first part of the proof we get the conclusion.
Remark 2.16.
Usually in the above result, we take  . Notice that in this case, condition (a) becomes
. Notice that in this case, condition (a) becomes
 , for each
, for each  and each
and each  .
.
Remark 2.17.
If in the above results we consider  , then we obtain, as consequences, several known results in the literature, as those given by M. Berinde and V. Berinde [8], Precup [5], Petruşel and Rus [11], and Feng and Liu [12]. Notice also that the theorems presented here represent extensions of some results given Bucur et al. [9], O'Regan and Precup [13], O'Regan et al. [7], Perov [1], and so forth.
, then we obtain, as consequences, several known results in the literature, as those given by M. Berinde and V. Berinde [8], Precup [5], Petruşel and Rus [11], and Feng and Liu [12]. Notice also that the theorems presented here represent extensions of some results given Bucur et al. [9], O'Regan and Precup [13], O'Regan et al. [7], Perov [1], and so forth.
Remark 2.18.
Notice also that since  is a particular type of cone in a Banach space, it is a nice direction of research to obtain extensions of these results for the case of operators on
is a particular type of cone in a Banach space, it is a nice direction of research to obtain extensions of these results for the case of operators on  -metric (or
-metric (or  -normed) spaces (see Zabrejko [14]). For other similar results, open questions, and research directions see [7, 11–13, 15–18].
-normed) spaces (see Zabrejko [14]). For other similar results, open questions, and research directions see [7, 11–13, 15–18].
References
Perov AI: On the Cauchy problem for a system of ordinary differential equations. Pviblizhen. Met. Reshen. Differ. Uvavn. 1964, 2: 115–134.
Varga RS: Matrix Iterative Analysis, Springer Series in Computational Mathematics. Volume 27. Springer, Berlin, Germany; 2000:x+358.
Allaire G, Kaber SM: Numerical Linear Algebra, Texts in Applied Mathematics. Volume 55. Springer, New York, NY, USA; 2008:xii+271.
Rus IA: Principles and Applications of the Fixed Point Theory. Dacia, Cluj-Napoca, Romania; 1979.
Precup R: The role of matrices that are convergent to zero in the study of semilinear operator systems. Mathematical and Computer Modelling 2009,49(3–4):703–708. 10.1016/j.mcm.2008.04.006
Turinici M: Finite-dimensional vector contractions and their fixed points. Studia Universitatis Babeş-Bolyai. Mathematica 1990,35(1):30–42.
O'Regan D, Shahzad N, Agarwal RP: Fixed point theory for generalized contractive maps on spaces with vector-valued metrics. In Fixed Point Theory and Applications. Vol. 6. Nova Science, New York, NY, USA; 2007:143–149.
Berinde M, Berinde V: On a general class of multi-valued weakly Picard mappings. Journal of Mathematical Analysis and Applications 2007,326(2):772–782. 10.1016/j.jmaa.2006.03.016
Bucur A, Guran L, Petruşel A: Fixed points for multivalued operators on a set endowed with vector-valued metrics and applications. Fixed Point Theory 2009,10(1):19–34.
Berinde V, Păcurar M: Fixed points and continuity of almost contractions. Fixed Point Theory 2008,9(1):23–34.
Petruşel A, Rus IA: Fixed point theory for multivalued operators on a set with two metrics. Fixed Point Theory 2007,8(1):97–104.
Feng Y, Liu S: Fixed point theorems for multi-valued contractive mappings and multi-valued Caristi type mappings. Journal of Mathematical Analysis and Applications 2006,317(1):103–112. 10.1016/j.jmaa.2005.12.004
O'Regan D, Precup R: Continuation theory for contractions on spaces with two vector-valued metrics. Applicable Analysis 2003,82(2):131–144. 10.1080/0003681031000063784
Zabrejko PP: -metric and -normed linear spaces: survey. Collectanea Mathematica 1997,48(4–6):825–859.
Chiş-Novac A, Precup R, Rus IA: Data dependence of fixed points for non-self generalized contractions. Fixed Point Theory 2009,10(1):73–87.
Rus IA, Petruşel A, Petruşel G: Fixed Point Theory. Cluj University Press, Cluj-Napoca, Romania; 2008:xx+509.
Chifu C, Petruşel G: Well-posedness and fractals via fixed point theory. Fixed Point Theory and Applications 2008, 2008:-9.
Voicu F: Fixed-point theorems in vector metric spaces. Studia Universitatis Babeş-Bolyai. Mathematica 1991,36(4):53–56.
Acknowledgments
The authors are thankful to anonymous reviewer(s) for remarks and suggestions that improved the quality of the paper. The first author wishes to thank for the financial support provided from programs co-financed by The Sectoral Operational Programme Human Resources Development, Contract POS DRU 6/1.5/S/3-"Doctoral studies: through science towards society".
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Filip, AD., Petruşel, A. Fixed Point Theorems on Spaces Endowed with Vector-Valued Metrics. Fixed Point Theory Appl 2010, 281381 (2010). https://doi.org/10.1155/2010/281381
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/281381
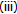 is replaced by
is replaced by in the estimation of
in the estimation of 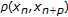 , presented in the proof of Theorem 2.12, we get
, presented in the proof of Theorem 2.12, we get 