- Research Article
- Open access
- Published:
Some Fixed Point Properties of Self-Maps Constructed by Switched Sets of Primary Self-Maps on Normed Linear Spaces
Fixed Point Theory and Applications volume 2010, Article number: 438614 (2010)
Abstract
This paper is devoted to the investigation of the existence of fixed points in a normed linear space  endowed with a norm
endowed with a norm  for self-maps
for self-maps  from
from  to
to  which are constructed from a given class of so-called primary self- maps being also from
which are constructed from a given class of so-called primary self- maps being also from  to
to  . The construction of the self-maps of interest is performed via a so-called switching rule which is a piecewise-constant map from a set
. The construction of the self-maps of interest is performed via a so-called switching rule which is a piecewise-constant map from a set  to some finite subset of the positive integers or a sequence map which domain in some discrete subset of
to some finite subset of the positive integers or a sequence map which domain in some discrete subset of  .
.
1. Introduction
This paper is devoted to the investigation of the existence of fixed points in a normed linear space  with norm
with norm  for self-maps from
for self-maps from  to
to  which are constructed from a given class of so-called primary self-maps from
which are constructed from a given class of so-called primary self-maps from  to
to  . The construction of the maps
. The construction of the maps  of interest is performed via a so-called switching rule
of interest is performed via a so-called switching rule  which is a piecewise-constant map from a set
which is a piecewise-constant map from a set  to some finite subset of the positive integers. The potential discontinuity points of such a self-map in a discrete subset
to some finite subset of the positive integers. The potential discontinuity points of such a self-map in a discrete subset  are the so-called switching points at which a new primary self-map in a class
are the so-called switching points at which a new primary self-map in a class  is activated to construct the self-map
is activated to construct the self-map  of interest, each of those self-maps depends also on some given switching rule
of interest, each of those self-maps depends also on some given switching rule  .
.
In particular,  , for all
, for all  where
where  are two consecutive elements in the sequence ST generated by the switching rule
are two consecutive elements in the sequence ST generated by the switching rule  such that
such that  , for all
, for all  , for all
, for all  provided that there is no
provided that there is no  .
.
The class of primary self-maps  used to generate the self-map
used to generate the self-map  from
from  to
to  might contain itself, in the most general case, a class of contractive primary self-maps from
might contain itself, in the most general case, a class of contractive primary self-maps from  to
to  , a class of large contractive self-maps from
, a class of large contractive self-maps from  to
to  , a class of nonexpansive self-maps from
, a class of nonexpansive self-maps from  to
to  , as well as a class of expansive self-maps from
, as well as a class of expansive self-maps from  to X. The problem is easily extendable to the case when the switching rule is a discrete sequence of domain in a discrete set of
to X. The problem is easily extendable to the case when the switching rule is a discrete sequence of domain in a discrete set of  and of codomain again being the set of nonnegative integers. The study is of particular interest for its potential application to the study of eventual fixed points in the state-trajectory solution of either continuous-time or discrete-time switched dynamic systems [1–6], constructed from a fixed set of primary parameterizations.
and of codomain again being the set of nonnegative integers. The study is of particular interest for its potential application to the study of eventual fixed points in the state-trajectory solution of either continuous-time or discrete-time switched dynamic systems [1–6], constructed from a fixed set of primary parameterizations.
It is well known that contractive self-maps in normed linear spaces and in metric spaces possess a fixed point which is unique in Banach spaces  and in complete metric spaces
and in complete metric spaces  , [7–10]. Under additional boundedness-type conditions, a large contractive self-map
, [7–10]. Under additional boundedness-type conditions, a large contractive self-map  from
from  to
to  which generates uniformly bounded iterates for any number of iterations still possesses a unique fixed point in a complete metric space
which generates uniformly bounded iterates for any number of iterations still possesses a unique fixed point in a complete metric space  (or in a Banach space
(or in a Banach space  [6]. Some nonexpansive self-maps as well as certain expansive self-maps also possess fixed points (see, e.g., [11, 12]). On the other hand, pseudocontractive self-maps and semicontinuous compact maps in Banach spaces can also possess fixed points [13, 14]. Those features motivate in this paper the choice of the given class of primary self-maps for this investigation. It is also taken into account as motivation that unforced linear time-invariant dynamic systems are exponentially stable to the origin if the matrix of dynamics is a stability matrix. In the case that such a matrix has some pair of complex conjugate eigenvalues then the solution is bounded and the solution trajectory may oscillate, and if there is some eigenvalue with positive real part (i.e., within the instability region), then the state trajectory solution is unbounded. The two first situations can be discussed using the fixed pointy formalism, [1, 2, 6]. Thus, it is of interest to have some extended formalism to investigate time-varying switched dynamic systems obtained under switched linear primary parameterizations not all of them being necessarily stable and then associated with asymptotic contractive self-maps. It is also of interest the basic investigation on the existence of fixed points of discontinuous self-maps which are identical to some self-maps in a prescribed class over each connected subset of
[6]. Some nonexpansive self-maps as well as certain expansive self-maps also possess fixed points (see, e.g., [11, 12]). On the other hand, pseudocontractive self-maps and semicontinuous compact maps in Banach spaces can also possess fixed points [13, 14]. Those features motivate in this paper the choice of the given class of primary self-maps for this investigation. It is also taken into account as motivation that unforced linear time-invariant dynamic systems are exponentially stable to the origin if the matrix of dynamics is a stability matrix. In the case that such a matrix has some pair of complex conjugate eigenvalues then the solution is bounded and the solution trajectory may oscillate, and if there is some eigenvalue with positive real part (i.e., within the instability region), then the state trajectory solution is unbounded. The two first situations can be discussed using the fixed pointy formalism, [1, 2, 6]. Thus, it is of interest to have some extended formalism to investigate time-varying switched dynamic systems obtained under switched linear primary parameterizations not all of them being necessarily stable and then associated with asymptotic contractive self-maps. It is also of interest the basic investigation on the existence of fixed points of discontinuous self-maps which are identical to some self-maps in a prescribed class over each connected subset of being generated from a switching rule
being generated from a switching rule of switching points in the sequence
of switching points in the sequence . The switching rule which governs the definition of the self-map
. The switching rule which governs the definition of the self-map  from
from  to
to  from the primary class of self-maps from
from the primary class of self-maps from  to
to  is shown to be crucial for
is shown to be crucial for  to possess a fixed point.
to possess a fixed point.  is assumed to be a normed linear space which is not necessarily either a Banach space or assumed to have some uniform structure [15].
is assumed to be a normed linear space which is not necessarily either a Banach space or assumed to have some uniform structure [15].
Three examples of the formalism are provided two of them being referred to the use of arbitrary primary self-maps on  while the third one refers to linear time-varying dynamic systems subject to simultaneous parameterization switching and impulsive controls.
while the third one refers to linear time-varying dynamic systems subject to simultaneous parameterization switching and impulsive controls.
2. Notation
 where
where  .
.
 where
where  .
.
 , respectively,
, respectively,  are the sets of
are the sets of  -real, respectively,
-real, respectively,  -complex vector functions of domain
-complex vector functions of domain  of class
of class  , that is,
, that is,  times
times  -real, respectively,
-real, respectively,  -complex continuously differentiable everywhere in its definition domain
-complex continuously differentiable everywhere in its definition domain  .
.
 , respectively,
, respectively,  are the sets of
are the sets of  -real or, respectively,
-real or, respectively,  -complex vector functions of domain
-complex vector functions of domain  of class
of class  with its
with its  th time derivative being necessarily everywhere piecewise-continuous in
th time derivative being necessarily everywhere piecewise-continuous in  . Thus,
. Thus,  , respectively,
, respectively,  are the sets of all
are the sets of all  -real, respectively,
-real, respectively,  -complex vector functions being piecewise—continuous everywhere in
-complex vector functions being piecewise—continuous everywhere in  .
.
If  is a first-class discontinuity point of
is a first-class discontinuity point of  , then
, then  , simplifying the customary notation
, simplifying the customary notation  , denotes the lower limit of
, denotes the lower limit of  at
at  and
and  denotes the right limit of
denotes the right limit of  at
at  .
.
 denotes the Lebesgue measure of a subset
denotes the Lebesgue measure of a subset  of
of  .
.
 is the discrete measure of the sequence
is the discrete measure of the sequence  (A being Lebesgue-measurable) defined via the Kronecker-delta defined by
(A being Lebesgue-measurable) defined via the Kronecker-delta defined by  if
if  and
and  , otherwise.
, otherwise.
The symbols  , and
, and  mean logic conjunction, disjunction, and negation, respectively, and
mean logic conjunction, disjunction, and negation, respectively, and  is a subset of the positive integer numbers.
is a subset of the positive integer numbers.
To establish the general framework for the formulation, consider a set  which is a proper or improper subset of
which is a proper or improper subset of  (it could also be a subset of
(it could also be a subset of  ) and
) and  being a linear normed space endowed with the norm
being a linear normed space endowed with the norm  .
.
Consider also a class of so-called primary (i.e., auxiliary) self-maps  , for all
, for all  to be used to build the class of maps under study through Fixed Point Theory which is defined by
to be used to build the class of maps under study through Fixed Point Theory which is defined by

The class  of primary self-maps of
of primary self-maps of  , which generate the class
, which generate the class  , is defined by
, is defined by  for some proper or improper subset
for some proper or improper subset  of
of  , for all
, for all  . In many applications
. In many applications  ; for all
; for all  . However, the possibility of taking different subsets
. However, the possibility of taking different subsets  of
of  remains open within this formulation, for instance, for cases when the various
remains open within this formulation, for instance, for cases when the various  parameterizations (or some of them) are not defined or, simply, not allowed to switch arbitrarily but each with its own switching restrictions. The map
parameterizations (or some of them) are not defined or, simply, not allowed to switch arbitrarily but each with its own switching restrictions. The map  (
( ) is the so-called switching rule being an integer-valued switching function if
) is the so-called switching rule being an integer-valued switching function if  is a subset of
is a subset of  of nonzero measure and a nonnegative integer-valued switching sequence of real domain if
of nonzero measure and a nonnegative integer-valued switching sequence of real domain if  is a subset of
is a subset of  . Each element of
. Each element of  for which the initial condition is fixed is also axiomatically considered a switching point for any arbitrary switching rule. That intuitively means that a switching rule involves a switch
for which the initial condition is fixed is also axiomatically considered a switching point for any arbitrary switching rule. That intuitively means that a switching rule involves a switch  . The discrete switching sequence
. The discrete switching sequence of switching points
of switching points  , indexed for
, indexed for  and which is generated by the switching rule
and which is generated by the switching rule  [3–5], is defined as follows,
[3–5], is defined as follows,

 is the number of switching points which is either finite or infinity numerable.
is the number of switching points which is either finite or infinity numerable.  (the so-called Switching Property of the switching rule
(the so-called Switching Property of the switching rule  ): the switching sequence ST is defined according to the
): the switching sequence ST is defined according to the  -Property:
-Property:

Note that each switching-dependent integer  is some integer in the set
is some integer in the set  which defines the configuration within the set of
which defines the configuration within the set of  configurations which remains active within the interval
configurations which remains active within the interval  for two consecutive switching points
for two consecutive switching points  so that for any three consecutive
so that for any three consecutive  ,
,

The discrete switching sequence  may also be viewed as a discrete strictly ordered set of real or integer nonnegative numbers of first element (i.e., first switching point)
may also be viewed as a discrete strictly ordered set of real or integer nonnegative numbers of first element (i.e., first switching point)  in the sense that
in the sense that  such that
such that  . Also,
. Also,  such that
such that  ; for all
; for all . Note that the switching sequence is a strictly ordered sequence of real numbers which depends on the switching rule
. Note that the switching sequence is a strictly ordered sequence of real numbers which depends on the switching rule  . If the switching rule is a piecewise continuous function, that is,
. If the switching rule is a piecewise continuous function, that is,  is a countable union of real intervals then its discontinuity point happen at points of ST since the function
is a countable union of real intervals then its discontinuity point happen at points of ST since the function  changes to another primary function being distinct from the previous one. It is being supposed through the manuscript that
changes to another primary function being distinct from the previous one. It is being supposed through the manuscript that  (being either
(being either  or
or  ) and
) and  .
.
The above framework is useful for examples of composed functions, multi-parameterizations of dynamic systems, and so forth involving mappings with some kind of switching. In particular, it is useful to investigate the stability and asymptotic stability of certain dynamic systems which switched parameterizations. Examples of problems situations adjusting to the above description are [3–5].
-
(a)
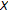 , a subset of
, a subset of 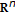 , is the state space of a continuous-time linear time-varying unforced dynamic system described for
, is the state space of a continuous-time linear time-varying unforced dynamic system described for 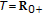 by
by 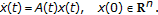 (2.5)
(2.5)
 is a real matrix function of piecewise constant entries whose image is
is a real matrix function of piecewise constant entries whose image is  , where
, where  , for all
, for all  with
with  if
if  .
.
Then,  where
where  is a fundamental matrix of (2.5), for all
is a fundamental matrix of (2.5), for all on the interval
on the interval  , for all
, for all and
and  is a piecewise constant function taking values in the integer set
is a piecewise constant function taking values in the integer set  which changes value at each
which changes value at each  so that
so that  , for all
, for all . The unique state trajectory-solution for each given initial conditions
. The unique state trajectory-solution for each given initial conditions  is
is  with
with  being differentiable everywhere in
being differentiable everywhere in  with
with  having first-class discontinuities in ST.
having first-class discontinuities in ST.
The eventual discontinuity points of the piecewise continuous switching function  , that is,
, that is,

are the discontinuity points of the state trajectory time-derivative  since they generate discontinuities in at least one entry of
since they generate discontinuities in at least one entry of  , for all
, for all  .
.
-
(b)
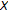 , a subset of
, a subset of  , is the state space of a discrete-time linear time-varying unforced dynamic system described for
, is the state space of a discrete-time linear time-varying unforced dynamic system described for 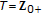 by
by  (2.7)
(2.7)
 is a real matrix sequence whose image is
is a real matrix sequence whose image is  , where
, where  , for all
, for all  .
.
The changes of value of the discrete switching function  at a sample
at a sample  imply changes of values in at least one entry of
imply changes of values in at least one entry of 
The class  of primary self-maps of
of primary self-maps of  is a union
is a union  of disjoint sets, of respective disjoint indexing sets
of disjoint sets, of respective disjoint indexing sets  and
and  whose sum of respective cardinals equalizes
whose sum of respective cardinals equalizes  that is
that is

with at least one of them being nonempty. Note from (2.1) that any function in  is constructed by taking a function in its primary class
is constructed by taking a function in its primary class  for each interval
for each interval  ; for all
; for all and some
and some  . In this way,
. In this way,  , with
, with  , is identical to some
, is identical to some  , for some
, for some  within each real interval
within each real interval  for each pair
for each pair  with the switching rule
with the switching rule  being defined in such a way that
being defined in such a way that  and
and  . Thus,
. Thus,  ; for all
; for all  . The sets
. The sets  and
and  considered in this section of the manuscript are defined in the sequel.
considered in this section of the manuscript are defined in the sequel.
-
(1)
The class
 of strictly contractive primary self-maps from
of strictly contractive primary self-maps from 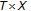 to
to 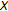 is defined as follows.
is defined as follows.
Definition 2.1.
 belongs to the class
belongs to the class  of strictly contractive primary self-maps from
of strictly contractive primary self-maps from  to
to  if for any
if for any  , for all
, for all  , the following inequality holds:
, the following inequality holds:

where  for some real constants
for some real constants  where
where  denotes the value in
denotes the value in  of
of  at
at  .
.
Note from Definition 2.1 that for each  in
in  it exists a function
it exists a function  for some real constant
for some real constant  , for all
, for all  . It is assumed that
. It is assumed that  is the first element in ST. The terminology "strictly contractive self-map" is used for the standard contractions referred to in the Banach contraction principle [6, 16] as a counterpart of the alternative terminology used for large contractions [6], here introduced below. Since strict contractions are also large contractions, since contractive self-maps are also nonexpansive ones, and since the sets
is the first element in ST. The terminology "strictly contractive self-map" is used for the standard contractions referred to in the Banach contraction principle [6, 16] as a counterpart of the alternative terminology used for large contractions [6], here introduced below. Since strict contractions are also large contractions, since contractive self-maps are also nonexpansive ones, and since the sets  and
and  are investigated as corresponding unions of disjoint components, the class of large contractions (resp., that of nonexpansive self-maps) are characterized as members of a set which excludes the strict contractions (resp., as members of a class which excludes any contractive self-map).
are investigated as corresponding unions of disjoint components, the class of large contractions (resp., that of nonexpansive self-maps) are characterized as members of a set which excludes the strict contractions (resp., as members of a class which excludes any contractive self-map).
Remark 2.2.
Note that the dependence of the functions  on the switching rule
on the switching rule  is a generalization which often occurs in practical cases. For instance, if a dynamic system (2.5) changes its parameterization at time
is a generalization which often occurs in practical cases. For instance, if a dynamic system (2.5) changes its parameterization at time  from a stability matrix
from a stability matrix  to another one
to another one  then
then  ; some
; some  so that
so that  , for all
, for all  what leads to
what leads to

for some sufficiently small real constant  if
if  . Since
. Since  is also a fundamental matrix of a time-invariant linear dynamic system (i.e., the active system parameterization starting at time
is also a fundamental matrix of a time-invariant linear dynamic system (i.e., the active system parameterization starting at time  ) for initial vector state
) for initial vector state  , then it is of exponential order so that
, then it is of exponential order so that  for
for  for some real constant
for some real constant  and some real constants
and some real constants  (being norm-dependent) and
(being norm-dependent) and  ;
;  .
.
-
(2)
The class
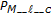 ofnonstrictly contractive large-contractive primary self-maps from
ofnonstrictly contractive large-contractive primary self-maps from 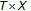 to
to 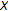 is now defined as follows.
is now defined as follows.
Definition 2.3.
 belongs to the class
belongs to the class  of nonstrictly contractive large-contractive primary self-maps from
of nonstrictly contractive large-contractive primary self-maps from  to
to  if it fulfils the joint condition
if it fulfils the joint condition  for any
for any  , for all
, for all , where Conditions
, where Conditions  and
and  are defined as follows.
are defined as follows.
(a) satisfies Condition
satisfies Condition 

(b) satisfies Condition
satisfies Condition  for all
for all  such that
such that

where  for some real constant
for some real constant  .
.
Definition 2.3 applies to all  in
in  with
with  for some real constant
for some real constant  , for all
, for all .
.
-
(3)
The class
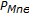 of noncontractive nonexpansive primary self-maps from
of noncontractive nonexpansive primary self-maps from  to
to  is defined as follows.
is defined as follows.
Definition 2.4.
 belongs to the class
belongs to the class  of noncontractive nonexpansive primary self-maps from
of noncontractive nonexpansive primary self-maps from  to
to  if for any
if for any  ,
,  , the following inequality holds:
, the following inequality holds:

Note that the above inequality is fulfilled by any  , for all
, for all  .
.
-
(4)
The class
 of expansive upper-bounded primary self-maps from
of expansive upper-bounded primary self-maps from 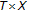 to
to 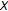 satisfying a global Lipschitz condition and an additional bounding property is now defined as follows.
satisfying a global Lipschitz condition and an additional bounding property is now defined as follows.
Definition 2.5.
 belongs to the class
belongs to the class  of expansive upper-bounded primary self-maps from
of expansive upper-bounded primary self-maps from  to
to  satisfying a global Lipschitz condition and an additional bounding property if for any
satisfying a global Lipschitz condition and an additional bounding property if for any  , the following inequalities hold:
, the following inequalities hold:

where  and
and  for some real constants
for some real constants  and
and  .
.
The above upper-bounding condition has been assumed to facilitate the subsequent exposition. Note that there exists  and
and  for some finite real constants
for some finite real constants  and
and  for any
for any  in
in  , for all
, for all  and that
and that  . Note also that this requirement is not very restrictive since it is fulfilled, for instance, by compact self-maps from
. Note also that this requirement is not very restrictive since it is fulfilled, for instance, by compact self-maps from  to
to  , also by bounded self-maps from
, also by bounded self-maps from  to
to  and, even, by unbounded piecewise-continuous maps of positive exponential order. That means that any state-trajectory solution generated from bounded initial conditions in globally exponentially stable continuous-time linear dynamic systems fulfil such a property for finite time in
and, even, by unbounded piecewise-continuous maps of positive exponential order. That means that any state-trajectory solution generated from bounded initial conditions in globally exponentially stable continuous-time linear dynamic systems fulfil such a property for finite time in  . Many nonlinear dynamic systems whose state-trajectory solutions do not exhibit finite escape times also possess this property.
. Many nonlinear dynamic systems whose state-trajectory solutions do not exhibit finite escape times also possess this property.
-
(5)
The class
 of neither nonexpansive nor expansive primary self-maps from
of neither nonexpansive nor expansive primary self-maps from 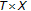 to
to 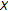 satisfying a global Lipschitz condition is defined in the sequel. This class includes, for instance, primary self-maps which are expansive and globally Lipschitzian and nonexpansive over alternate subsets of
satisfying a global Lipschitz condition is defined in the sequel. This class includes, for instance, primary self-maps which are expansive and globally Lipschitzian and nonexpansive over alternate subsets of  of finite measure and primary functions which are, for instance, asymptotically nonexpansive while being expansive for proper (then finite) subsets
of finite measure and primary functions which are, for instance, asymptotically nonexpansive while being expansive for proper (then finite) subsets  .
.
Definition 2.6.
 belongs to the class
belongs to the class  of neither nonexpansive nor expansive primary self-maps from
of neither nonexpansive nor expansive primary self-maps from  to
to  satisfying a global Lipschitz condition if it satisfies the following inequality:
satisfying a global Lipschitz condition if it satisfies the following inequality:

where  is uniformly upper-bounded by some finite real constant
is uniformly upper-bounded by some finite real constant  .
.
There exist  being uniformly upper-bounded by some finite real constants
being uniformly upper-bounded by some finite real constants  , for each
, for each  in
in  , for all
, for all  . Note that
. Note that 
Since  , and all the self-mappings
, and all the self-mappings  from
from  to
to  in all the component subsets satisfy a global Lipschitz condition, the following result is direct via recursion for each pair of consecutive elements of
in all the component subsets satisfy a global Lipschitz condition, the following result is direct via recursion for each pair of consecutive elements of  from the definition of the class of primary functions
from the definition of the class of primary functions  for
for  as a union of disjoint classes and Definition 2.1 and Definitions 2.3–2.6.
as a union of disjoint classes and Definition 2.1 and Definitions 2.3–2.6.
Lemma 2.7.
 , being generated from a class of primary self-maps
, being generated from a class of primary self-maps  of
of  in
in  by any switching rule
by any switching rule  , possesses the two following properties:
, possesses the two following properties:
-
(i)
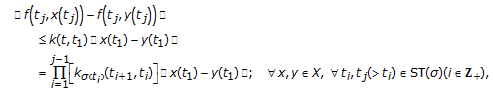 (2.16)
(2.16)
-
(ii)
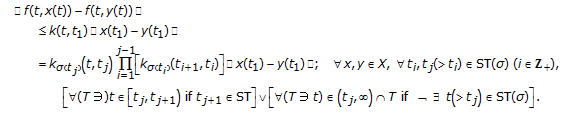 (2.17)
(2.17)
Proof.
Any function  in
in  is constructed for each interval
is constructed for each interval  by taking a function in its primary class
by taking a function in its primary class  , for all
, for all  and some
and some  . In this way,
. In this way,  , with
, with  , is identical to some
, is identical to some  , for some
, for some  within each real interval
within each real interval  for each pair
for each pair  with the switching rule
with the switching rule  being defined in such a way that
being defined in such a way that  and
and  . Thus,
. Thus,  , for all
, for all  . The primary class consists of a disjoint union of classes defined in Definition 2.1 and Definitions 2.3–2.6 which all have upper-bounding functions of the form of the first inequality in (2.16). The function
. The primary class consists of a disjoint union of classes defined in Definition 2.1 and Definitions 2.3–2.6 which all have upper-bounding functions of the form of the first inequality in (2.16). The function  can be directly expanded for any
can be directly expanded for any  and
and  , provided that some next consecutive
, provided that some next consecutive  exists, and for any
exists, and for any  , otherwise (i.e., if switching ends, i.e.,
, otherwise (i.e., if switching ends, i.e.,  has finite cardinal, and the last switching point is
has finite cardinal, and the last switching point is  ) via recursion from the preceding interswitching intervals
) via recursion from the preceding interswitching intervals  ;
;  , for all
, for all .
.
Remark 2.8.
The last logic proposition for the validity of Property (ii) of Lemma 2.7 means that  if
if  and, otherwise, that is, if
and, otherwise, that is, if  so that
so that  is the last element in ST (with the physical sense that the switching process generated by the switch rule
is the last element in ST (with the physical sense that the switching process generated by the switch rule  stops in finite time), then
stops in finite time), then  .
.
Lemma 2.7(ii) leads to the following direct consequent result.
Lemma 2.9.
Assume that  is Lebesgue-mesasurable with
is Lebesgue-mesasurable with  . Then, the self-map
. Then, the self-map  , being generated from a class of primary self-maps
, being generated from a class of primary self-maps  from
from  to
to  , which satisfies the given assumptions, from the switching rule
, which satisfies the given assumptions, from the switching rule  , is strictly contractive if there exists some finite
, is strictly contractive if there exists some finite  with
with  such that
such that

with  for all
for all  ,
,  . The condition (2.18) implies
. The condition (2.18) implies

where  , for all
, for all  ,
,  , and also
, and also

where  , for all
, for all  ,
,  .
.
The self-map  is still strictly contractive if (2.18) holds by replacing
is still strictly contractive if (2.18) holds by replacing  for some finite
for some finite  even if
even if  .
.
Proof.
It follows that if (2.18) holds, then proceeding inductively

so that one gets

so that  , being generated from a classof primary self-maps
, being generated from a classof primary self-maps  from
from  to
to  from the switching rule
from the switching rule  , is strictly contractive from Banach's contraction principle. Equations (2.19) and (2.20) are a direct consequence of the fact that (2.18) implies directly
, is strictly contractive from Banach's contraction principle. Equations (2.19) and (2.20) are a direct consequence of the fact that (2.18) implies directly

The second part of the result is obvious since the finite interval  of
of  may be removed from the discussion by still keeping the strict contraction property.
may be removed from the discussion by still keeping the strict contraction property.
To discuss some practical situations that guarantee the fulfilment of the condition (2.18), let us define the following subsets  of
of  , as a union of disjoint components associated with some proper or improper subset of the class of primary functions being active to build
, as a union of disjoint components associated with some proper or improper subset of the class of primary functions being active to build  each on some nonempty subset of the subset
each on some nonempty subset of the subset  of
of  :
:

with

being such that 


where  for any
for any  such that
such that  for any proper or improper subset of
for any proper or improper subset of  and
and

Note that  depends on
depends on  , but not on the
, but not on the  , since a particular switching rule can remove some primary self-maps from generating a particular self-map from
, since a particular switching rule can remove some primary self-maps from generating a particular self-map from  to
to  . Note also that the above decompositions are also extendable "mutatis-mutandis" to any subsets
. Note also that the above decompositions are also extendable "mutatis-mutandis" to any subsets  and
and  .
.
The interpretation of  is the number of strictly contractive primary self-maps from
is the number of strictly contractive primary self-maps from  to
to  ; that is, members of
; that is, members of  being active on any of the subsets of finite measure of
being active on any of the subsets of finite measure of  . Note that the sets
. Note that the sets  and
and  are, respectively, the set of switching points used to build
are, respectively, the set of switching points used to build  from the primary class of functions
from the primary class of functions  on
on  by the switching rule and
by the switching rule and  which restrict its image (since its domain is restricted) to some
which restrict its image (since its domain is restricted) to some which is the subset of active primary functions for some nonempty subset of
which is the subset of active primary functions for some nonempty subset of  . The interpretations of the disjoint decompositions of, in general, nonconnected subsets, of the sets
. The interpretations of the disjoint decompositions of, in general, nonconnected subsets, of the sets  and ST in (2.28) are related to. Note that for any given
and ST in (2.28) are related to. Note that for any given  , one has by construction
, one has by construction


where the sets  are connected disjoint subsets of
are connected disjoint subsets of  since
since  and
and  are consecutive switching points under the switching rule
are consecutive switching points under the switching rule  ,
,  if
if  (i.e., infinity numerable if
(i.e., infinity numerable if  generates infinitely many switching points), and
generates infinitely many switching points), and  with
with  and
and  , otherwise. However, the subsets
, otherwise. However, the subsets  and
and  of
of  are not necessarily connected for any given switching rule
are not necessarily connected for any given switching rule  since it can make a particular primary function at disjoint subsets of
since it can make a particular primary function at disjoint subsets of  active to build
active to build 
Note that the set  also includes any subset being obtained by replacing
also includes any subset being obtained by replacing  in (2.30) with any other of the disjoint components of
in (2.30) with any other of the disjoint components of  . Note also that Condition (2.18) needs the presence of a strictly contractive self-map as a member of the primary functions for the given switching rule as it is discussed in the subsequent result.
. Note also that Condition (2.18) needs the presence of a strictly contractive self-map as a member of the primary functions for the given switching rule as it is discussed in the subsequent result.
Lemma 2.10.
A necessary condition for the strict contractive condition (2.18) to hold is that switching rule  which generates
which generates  has at least one self-map
has at least one self-map  being a member of the primary self-maps
being a member of the primary self-maps  .
.
Proof.
Proceed by contradiction by assuming that the generalized condition obtained from (2.18) for any finite  holds with
holds with  . If
. If  then
then  and then (2.18) does not hold and, instead, we have,
and then (2.18) does not hold and, instead, we have,

so that

and, then, either

provided that it exists, or if the above limit does not exist, then  is not strictly contractive. A second possibility is
is not strictly contractive. A second possibility is  and
and  so that
so that  . Then, for any such a
. Then, for any such a 

Now, if  then the same contradiction as above follows. Otherwise, if
then the same contradiction as above follows. Otherwise, if  then either
then either  fails, for all
fails, for all , or it holds for some
, or it holds for some  but there is no
but there is no  such that (2.18) holds since it has been assumed that
such that (2.18) holds since it has been assumed that  satisfies
satisfies  .
.
Remark 2.11.
Concerning Lemma 2.10, note that fixed points can still exist for  even if
even if  . A such a situation can happen, for instance, if a self-map
. A such a situation can happen, for instance, if a self-map  of
of  is built with a switching rule
is built with a switching rule  involving above primary functions in a class
involving above primary functions in a class  . It is well known that a large contraction self-map in a Banach space can possess fixed points (see, e.g., [6]). However, Lemma 2.10 proves that if
. It is well known that a large contraction self-map in a Banach space can possess fixed points (see, e.g., [6]). However, Lemma 2.10 proves that if  , the strict contraction condition (2.18) does not hold for any
, the strict contraction condition (2.18) does not hold for any 
The mains result of this section follows.
Theorem 2.12.
Assume that  is Lebesgue-mesasurable with
is Lebesgue-mesasurable with  and consider a switching rule
and consider a switching rule  which generates
which generates  , with
, with  defined by the class
defined by the class  of primary self-maps from
of primary self-maps from  to
to  satisfying the given assumptions. The following properties hold.
satisfying the given assumptions. The following properties hold.
(i) has a fixed point under Lemma 2.9 if
has a fixed point under Lemma 2.9 if  and
and 
(ii) has a fixed point if
has a fixed point if  and
and  and, furthermore,
and, furthermore,  such that the boundedness condition
such that the boundedness condition

holds in the case that  is not Lipschitzian.
is not Lipschitzian.
(iii) has a fixed point if
has a fixed point if  and
and  and, furthermore,
and, furthermore,  such that the boundedness condition
such that the boundedness condition

holds in the case that  is not Lipschitzian; then
is not Lipschitzian; then  has a fixed point.
has a fixed point.
Proof.
-
(i)
Proceed by contradiction by taking into account the set inclusion properties (2.30) and by assuming that the extended form of (2.18) in Lemma 2.9 to any replacement
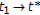 (finite) does not hold. Since
(finite) does not hold. Since  and
and  , there exists a finite
, there exists a finite 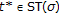 such that
such that  for
for 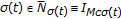 ; for all
; for all 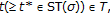 and for
and for 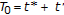 (some finite
(some finite 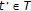 ), it follows by complete induction that
), it follows by complete induction that  (2.37)
(2.37)
for some  since
since  , for all
, for all  which is a contradiction. Then, Lemma 2.9 holds with
which is a contradiction. Then, Lemma 2.9 holds with  for the valid replacement
for the valid replacement  so that
so that  is strictly contractive and has a fixed point.
is strictly contractive and has a fixed point.
-
(ii)
Since
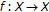 is a large contraction, the real sequence below
is a large contraction, the real sequence below 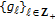 is bounded monotonically strictly decreasing for any pair
is bounded monotonically strictly decreasing for any pair 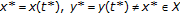 since
since 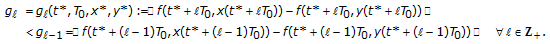 (2.38)
(2.38)
Thus, for any prefixed  and
and  such that
such that

provided that  is sufficiently close to zero satisfying
is sufficiently close to zero satisfying  where
where  is the Lipschitz constant of the self-map
is the Lipschitz constant of the self-map  from
from  to
to  , provided to be Lipschitzian, and any given
, provided to be Lipschitzian, and any given  . If
. If  as
as  , then the self-map
, then the self-map  from
from  to
to  has a fixed point in
has a fixed point in  and the result is proven. Furthermore, the error sequence
and the result is proven. Furthermore, the error sequence  which maps
which maps  in
in  is a Cauchy sequence and has a zero fixed point in
is a Cauchy sequence and has a zero fixed point in  . Also,
. Also,  is a Cauchy sequence with a limit in
is a Cauchy sequence with a limit in  which is a fixed point of
which is a fixed point of  . Otherwise, assume that
. Otherwise, assume that  such that
such that  is not a Cauchy sequence or, if so, it does not converge to zero while satisfying
is not a Cauchy sequence or, if so, it does not converge to zero while satisfying  ; for all
; for all  Then,
Then,  such that
such that

Then, there is a finite sufficiently large  such that the above result is a contradiction for all
such that the above result is a contradiction for all  . Then, the self-map the Lipschitzian self-map
. Then, the self-map the Lipschitzian self-map  from
from  to
to  has a fixed point in
has a fixed point in  . Now, if
. Now, if  is not Lipschitzian, but it satisfies the given boundedness alternative condition, then
is not Lipschitzian, but it satisfies the given boundedness alternative condition, then

which is again a contradiction for for all  such that
such that  concluding that
concluding that  has a fixed point.(iii)Since
has a fixed point.(iii)Since  then either
then either
(1) and then the proof follows from Property (i), or
and then the proof follows from Property (i), or
(2) and then the proof follows from Property (ii), or
and then the proof follows from Property (ii), or
(3) and then the proof also follows from Property (ii).
and then the proof also follows from Property (ii).
Remark 2.13 (An interpretation of Theorem 2.12).
Theorem 2.12 extends the Banach contraction principle of strictly contractive maps and the fixed point properties of large contractions to the case when the self-map is defined via switching-based combination of contractive primary self-maps as follows. If  , then the self-map
, then the self-map  from
from  to
to  is built with a set of strictly contractive self-maps from
is built with a set of strictly contractive self-maps from  to
to  on a subset of its domain of infinity Lebesgue measure. If, furthermore,
on a subset of its domain of infinity Lebesgue measure. If, furthermore,  , then there is a finite
, then there is a finite  (e.g., a finite time instant if
(e.g., a finite time instant if  ) such that all the primary self-maps used to build the self-map
) such that all the primary self-maps used to build the self-map  are strictly contractive for all
are strictly contractive for all  . A conclusion is that the self-map
. A conclusion is that the self-map  from
from  to
to  is strictly contractive so that it has a fixed point. A close reasoning leads to the conclusion that the self-map
is strictly contractive so that it has a fixed point. A close reasoning leads to the conclusion that the self-map  from
from  to
to  is a large contraction if
is a large contraction if  and
and  or if
or if  and
and  . In all those cases, the subset of the domain of
. In all those cases, the subset of the domain of  where each primary self-map is activated by the switching rule
where each primary self-map is activated by the switching rule  are not necessarily connected. In the case when
are not necessarily connected. In the case when  (Theorem 2.12(iii)) the joint subset of the domain of
(Theorem 2.12(iii)) the joint subset of the domain of  where the primary self-maps building
where the primary self-maps building  are either strictly contractive or large contractive has infinite measure, what leads to the same conclusions about the existence of fixed points as in the two former cases, although it is not necessarily connected. A counterpart of Theorem 2.12 can be formulated for the case when
are either strictly contractive or large contractive has infinite measure, what leads to the same conclusions about the existence of fixed points as in the two former cases, although it is not necessarily connected. A counterpart of Theorem 2.12 can be formulated for the case when  is discrete countable sequence (say, e.g.,
is discrete countable sequence (say, e.g.,  ). In this case, the finite Lebesgue measures referred to in Theorem 2.12 are replaced by the cardinals of finite subsequences of
). In this case, the finite Lebesgue measures referred to in Theorem 2.12 are replaced by the cardinals of finite subsequences of  and the infinity Lebesgue measures are replaced by
and the infinity Lebesgue measures are replaced by  (i.e., sequences of countable infinity many nonnegative integers). The usefulness of the extended results ofTheorem 2.12relies on its use on the stability properties of switched dynamic systems with asymptotic convergence of their state trajectory solutions to a fixed point. They also rely, to a more basic level, on the fixed point properties of maps which are not necessarily Lipschitz-continuous but being built with Lipschitz-continuous functions through a switching process.
(i.e., sequences of countable infinity many nonnegative integers). The usefulness of the extended results ofTheorem 2.12relies on its use on the stability properties of switched dynamic systems with asymptotic convergence of their state trajectory solutions to a fixed point. They also rely, to a more basic level, on the fixed point properties of maps which are not necessarily Lipschitz-continuous but being built with Lipschitz-continuous functions through a switching process.
Remark 2.14.
In the case that  the existence of a fixed point is not guaranteed under the given conditions. Some "ad hoc" conditions for the existence of fixed points are given in the next section.
the existence of a fixed point is not guaranteed under the given conditions. Some "ad hoc" conditions for the existence of fixed points are given in the next section.
Remark 2.15.
If a fixed point exists for a particular self-map  built with a class
built with a class  of
of  primary self-maps switched according to a rule
primary self-maps switched according to a rule  under the sufficiency-type conditions of Theorem 2.12, then such a fixed point is unique in the Banach space
under the sufficiency-type conditions of Theorem 2.12, then such a fixed point is unique in the Banach space  . The result is directly extendable to complete metric spaces
. The result is directly extendable to complete metric spaces  what allows to consider a parallel formulation for the case that the domain of
what allows to consider a parallel formulation for the case that the domain of  , that is
, that is  , is an infinite sequence on nonnegative real numbers. If the formalism is applied on a compact metric space, then it is not required for large contractions the fulfilment of the boundedness condition of Theorem 2.12(ii)-(iii) from Edelstein fixed point theorem [8] which can be proven using the Meir-Keeler theorem [9] as observed in [10].
, is an infinite sequence on nonnegative real numbers. If the formalism is applied on a compact metric space, then it is not required for large contractions the fulfilment of the boundedness condition of Theorem 2.12(ii)-(iii) from Edelstein fixed point theorem [8] which can be proven using the Meir-Keeler theorem [9] as observed in [10].
The following property from  to
to  being a fixed point space relative to a set of maps [16] is obvious under the conditions which guarantee the existence of at least a fixed point in
being a fixed point space relative to a set of maps [16] is obvious under the conditions which guarantee the existence of at least a fixed point in  for any
for any  in the class
in the class  .
.
Assertion 2.16.
The Banach space  is a fixed point space relative to the class of self-maps
is a fixed point space relative to the class of self-maps  which satisfies any of the properties of Theorem 2.12.
which satisfies any of the properties of Theorem 2.12.
Example 2.17.
Consider  and a set
and a set  of
of  primary self-maps
primary self-maps  all having the structure
all having the structure

for some given  (being piecewise continuous and uniformly bounded on
(being piecewise continuous and uniformly bounded on  );
);  , for all
, for all  . Note that the primary self-maps depend on a switching rule
. Note that the primary self-maps depend on a switching rule  which is a piecewise constant real function defined as
which is a piecewise constant real function defined as  , for all
, for all  where
where  is the switching sequence. The class
is the switching sequence. The class  consists of the piecewise continuous self-maps f on
consists of the piecewise continuous self-maps f on  built as follows:
built as follows:

Note that  , for all
, for all  , for all
, for all 
If  , for all
, for all  then
then

Theorem 2.12 is applied as follows. If all the primary self-maps are strictly contractive for the switching rule  , that is,
, that is,  , for all
, for all  that is, a sufficiently fast switching cadence is used, it follows that the real self-map possesses a fixed point from Banach contraction principle for any switching rule. It is not difficult to see that the property also holds if the primary self-maps are large contractions or there are mixed large and strict contractions used by the switching rule to build the self-map
that is, a sufficiently fast switching cadence is used, it follows that the real self-map possesses a fixed point from Banach contraction principle for any switching rule. It is not difficult to see that the property also holds if the primary self-maps are large contractions or there are mixed large and strict contractions used by the switching rule to build the self-map  Each particular fixed point may depend on the switching rule and
Each particular fixed point may depend on the switching rule and  is a fixed point space for the class
is a fixed point space for the class  of self-maps built in such a way. The property may be generalized by using also primary nonexpansive maps with associated
of self-maps built in such a way. The property may be generalized by using also primary nonexpansive maps with associated  having unity absolute upper-bound provided that the switching rule involves nonexpansive self-maps being always used on subsets of
having unity absolute upper-bound provided that the switching rule involves nonexpansive self-maps being always used on subsets of  of finite Lebesgue measure or, otherwise, combined with contractive primary self-maps both (alternately) run on sets of infinity Lebesgue measure. If
of finite Lebesgue measure or, otherwise, combined with contractive primary self-maps both (alternately) run on sets of infinity Lebesgue measure. If  has also nonexpansive self maps, then a fixed point does not exist for all the class
has also nonexpansive self maps, then a fixed point does not exist for all the class  of constructed self-maps so that
of constructed self-maps so that  is not a fixed point space. Finally, if expansive primary self-maps are also considered, then a fixed point still exists for switching rules satisfying a condition like that of Lemma 2.9 for some finite real
is not a fixed point space. Finally, if expansive primary self-maps are also considered, then a fixed point still exists for switching rules satisfying a condition like that of Lemma 2.9 for some finite real  according to the following constraint:
according to the following constraint:

for some real constant  , where
, where

The above results are directly extendable to the linear space  endowed with any Euclidean norm.
endowed with any Euclidean norm.
Example 2.18.
If the replacements  , are performed in (2.42) to define the class of primary self-maps, that is, a sufficiently slow switching cadence is used, then, the residence interval taken for the next switch after the switch at
, are performed in (2.42) to define the class of primary self-maps, that is, a sufficiently slow switching cadence is used, then, the residence interval taken for the next switch after the switch at  makes to strictly decrease the function
makes to strictly decrease the function  . As a result, the existence of a fixed point is guaranteed by any switching rule involving at least a primary self-map generating
. As a result, the existence of a fixed point is guaranteed by any switching rule involving at least a primary self-map generating  or sufficiently large residence intervals compared with the times where the remaining primary self-maps are used to generate
or sufficiently large residence intervals compared with the times where the remaining primary self-maps are used to generate  .
.
3. Some Extensions
It is now assumed that the class  of primary self-maps from
of primary self-maps from  to
to  still satisfies weaker assumptions than the given ones in the previous section as follows.
still satisfies weaker assumptions than the given ones in the previous section as follows.
 The real constants
The real constants  are not necessarily upper-bounds for the primary self-maps
are not necessarily upper-bounds for the primary self-maps  from
from  to
to  in
in  . Instead, the class
. Instead, the class  is redefined so that the upper-bounding functions
is redefined so that the upper-bounding functions  , for all
, for all  , for all
, for all are assumed to be nonnegative and uniformly upper-bounded by finite constants
are assumed to be nonnegative and uniformly upper-bounded by finite constants  (possibly exceeding or being equal to unity within some subsets of their definition domains) on
(possibly exceeding or being equal to unity within some subsets of their definition domains) on  . Furthermore, they are assumed to be asymptotically strictly contractive (i.e., taking asymptotically values being less than unity) in the precise sense that
. Furthermore, they are assumed to be asymptotically strictly contractive (i.e., taking asymptotically values being less than unity) in the precise sense that  for some
for some  . Note that this condition implies that for any given
. Note that this condition implies that for any given  with arbitrary
with arbitrary  such that
such that  , the upper-bounding function
, the upper-bounding function  associated with
associated with  satisfies the limiting upper-bounding condition
satisfies the limiting upper-bounding condition  .
.
Note that the condition  is fulfilled if
is fulfilled if  is uniformly bounded in
is uniformly bounded in  and it is also monotone strictly decreasing on some
and it is also monotone strictly decreasing on some  . In this case, there is also a subinterval
. In this case, there is also a subinterval  in which
in which  , for all
, for all  . This condition is important in practice since exponentially stable dynamics such as those in (2.5) systems fulfil it. Thus, it is possible to construct switching rules which respect a sufficiently large minimum residence time interval at least at one of their stable parameterizations to guarantee the existence of a fixed point and the exponential stability to the origin in the dynamic system is unforced as a result.
. This condition is important in practice since exponentially stable dynamics such as those in (2.5) systems fulfil it. Thus, it is possible to construct switching rules which respect a sufficiently large minimum residence time interval at least at one of their stable parameterizations to guarantee the existence of a fixed point and the exponential stability to the origin in the dynamic system is unforced as a result.
 The class
The class  is assumed to be the set of asymptotically large contractive primary self-maps from
is assumed to be the set of asymptotically large contractive primary self-maps from  to
to  in the sense that Condition
in the sense that Condition  for any primary self-map
for any primary self-map  from
from  to
to  in the class
in the class  is replaced with its asymptotic counterpart:
is replaced with its asymptotic counterpart:

so that  fulfils the strict upper-bounding condition in some subset of
fulfils the strict upper-bounding condition in some subset of  of infinite Lebesgue measure. The Condition
of infinite Lebesgue measure. The Condition  is left unaltered.
is left unaltered.
 The class of noncontractive nonexpansive self-maps
The class of noncontractive nonexpansive self-maps  from
from  to
to  is defined to fulfil a similar condition to the above one by using instead under nonstrict inequality.
is defined to fulfil a similar condition to the above one by using instead under nonstrict inequality.
 The remaining classes of primary functions are assumed to be as those given in Section 2.
The remaining classes of primary functions are assumed to be as those given in Section 2.
Although three of the subsets of primary self-maps are redefined under weaker conditions, the notation of Section 2 is kept for them in order to facilitate the exposition. The subsequent notation  , for
, for  , stands for switching points of
, stands for switching points of  the rule
the rule  acting on the primary class
acting on the primary class  of self-maps from
of self-maps from  to
to  being within the subset
being within the subset  If the arguments and
If the arguments and  are omitted, then
are omitted, then  is understood to be within any subset of
is understood to be within any subset of  .
.
The main result of this section extends Theorem 2.12 as follows.
Theorem 3.1.
Under the assumptions in this section, assume also that all the self-maps of the class  in
in  are also uniformly bounded, that
are also uniformly bounded, that  is Lebesgue-measurable with
is Lebesgue-measurable with  and consider a switching rule
and consider a switching rule  which generates
which generates  , with
, with  defined by the set
defined by the set  of primary self-maps from
of primary self-maps from  to
to  satisfying all the above assumptions. The following properties hold.
satisfying all the above assumptions. The following properties hold.
(i) has a fixed point if
has a fixed point if  ,
,  and a minimum finite residence interval
and a minimum finite residence interval  being sufficiently large compared to
being sufficiently large compared to  is respected at any
is respected at any  , for all
, for all  before the next switching in the following precise sense:
before the next switching in the following precise sense:

or there is a finite number of switches with the last switching point being to a primary self-map in  .
.
(ii) has a fixed point if
has a fixed point if  and
and  and, furthermore,
and, furthermore,  such that the boundedness condition
such that the boundedness condition

holds in the case that  is not Lipschitzian, then
is not Lipschitzian, then  has a fixed point and a minimum finite residence interval
has a fixed point and a minimum finite residence interval  being sufficiently large compared to
being sufficiently large compared to  is respected at any
is respected at any  , for all
, for all  .
.
(iii) has a fixed point if
has a fixed point if  and
and  and, furthermore,
and, furthermore,  such that the boundedness condition
such that the boundedness condition

holds in the case that  is not Lipschitzian, then
is not Lipschitzian, then  has a fixed point providing that a minimum residence interval is respected for at least one of the asymptotically strictly contractive or asymptotically large contractive self-maps in
has a fixed point providing that a minimum residence interval is respected for at least one of the asymptotically strictly contractive or asymptotically large contractive self-maps in  .
.
Proof.
-
(i)
Assume
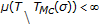 ,
,  . Since
. Since  is uniformly bounded piecewise-continuous since all the functions in
is uniformly bounded piecewise-continuous since all the functions in 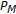 are also uniformly bounded, the corresponding rate over-bounding functions
are also uniformly bounded, the corresponding rate over-bounding functions 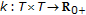 are also uniformly bounded. Then, since
are also uniformly bounded. Then, since 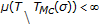 , then the following situations can occur.
, then the following situations can occur.
 The last switching occurs at a finite point
The last switching occurs at a finite point  in
in  with switching of the self-map
with switching of the self-map  from
from  to
to  to an asymptotically contractive primary self-map. Also,
to an asymptotically contractive primary self-map. Also,  is the left boundary of a connected interval of
is the left boundary of a connected interval of  being of infinity Lebesgue measure. Formally:
being of infinity Lebesgue measure. Formally: such that
such that  for some
for some  , that is, there is no switching point being larger than the largest switching point
, that is, there is no switching point being larger than the largest switching point  in ST under the switching rule
in ST under the switching rule  . Then,
. Then,

provided that  for any given positive real constant
for any given positive real constant  such that
such that  is sufficiently large but finite since
is sufficiently large but finite since  . Thus, the self-map
. Thus, the self-map  has a fixed point.
has a fixed point.
 There is no last switching point but after a finite switching points all the switching points exceeding some sufficiently large finite one involve switches to asymptotically strictly contractive primary self-maps from
There is no last switching point but after a finite switching points all the switching points exceeding some sufficiently large finite one involve switches to asymptotically strictly contractive primary self-maps from  to
to  .
.
Then,  such that
such that  and
and  for some
for some  . First, assume that
. First, assume that  and
and  generates the next switching point
generates the next switching point  under a primary self-map in
under a primary self-map in  with
with  , and
, and

This situation can occur of a simply connected subinterval  of
of  Using a parallel reasoning to that of case (
Using a parallel reasoning to that of case ( involving complete induction, one gets that
involving complete induction, one gets that  since
since

with  provided that
provided that  if
if  for some
for some  with
with  being sufficiently large but finite. It is again concluded that the self-map
being sufficiently large but finite. It is again concluded that the self-map  has a fixed point.
has a fixed point.
 There is no last switching point but, after a finite switching point, the sequence of all the switching points exceeding some sufficiently large finite one contains an infinite sequence of switching points to primary self-maps from
There is no last switching point but, after a finite switching point, the sequence of all the switching points exceeding some sufficiently large finite one contains an infinite sequence of switching points to primary self-maps from  to
to  which are not asymptotically contractive. This case cannot occur since then
which are not asymptotically contractive. This case cannot occur since then  contradicting the given assumptions.
contradicting the given assumptions.
Property (i) has been fully proven.
Properties (ii)-(iii) are proven in a similar way to their stronger parallel properties in Theorem 2.12 by using the upper-bounding limiting property of (2.18) for the extended class of primary self-maps. The detailed proof is omitted.
Corollary 3.2.
Theorem 3.1(i) is fulfilled for any switching rule such that the minimum residence intervals referred to are respected in only one of the asymptotically strictly contractive primary self-maps. Theorem 3.1(ii) is extendable to the fulfilment of a sufficiently large residence interval by one of the asymptotically large contractive primary self-maps. Theorem 3.1(iii) is extendable to the fulfilment of the above property by either one of the asymptotically strictly contractive or one of the asymptotically large contractive primary self-maps.
Theorem 3.1 addresses the case when the subset of  , where
, where  is defined via not asymptotically (strict or large) contractive primary self-maps in
is defined via not asymptotically (strict or large) contractive primary self-maps in  , has a finite Lebesgue measure; that is, switches in-between primary self-maps can involve no contractive self-maps over finite intervals. It is furthermore interesting to make that assumption more powerful by considering that
, has a finite Lebesgue measure; that is, switches in-between primary self-maps can involve no contractive self-maps over finite intervals. It is furthermore interesting to make that assumption more powerful by considering that  is the countable union of infinitely many connected subsets of finite Lebesgue measure whose boundaries are each pair of consecutive switching points. Sets formed by unions of some finite number of those subsets for consecutive switching points are assumed to contain at least one asymptotically either strict or large contractive primary self-map generating
is the countable union of infinitely many connected subsets of finite Lebesgue measure whose boundaries are each pair of consecutive switching points. Sets formed by unions of some finite number of those subsets for consecutive switching points are assumed to contain at least one asymptotically either strict or large contractive primary self-map generating  . The subsequent result extends Theorem 3.1 to the case when the conditions of Lemma 2.9 are modified to their asymptotic versions. It is admitted that the sets of primary self-maps which are not contractive may be asymptotically compensated by the contractive ones, so that the built
. The subsequent result extends Theorem 3.1 to the case when the conditions of Lemma 2.9 are modified to their asymptotic versions. It is admitted that the sets of primary self-maps which are not contractive may be asymptotically compensated by the contractive ones, so that the built by the switching rule
by the switching rule is asymptotically contractive in some sense to guarantee the existence of a fixed point. Its proof follows directly by combining a directly extended Lemma 2.9 to its asymptotic version with Theorem 3.1 since any
is asymptotically contractive in some sense to guarantee the existence of a fixed point. Its proof follows directly by combining a directly extended Lemma 2.9 to its asymptotic version with Theorem 3.1 since any  is uniformly bounded on its definition domain.
is uniformly bounded on its definition domain.
Corollary 3.3.
Assume that all the self-maps of the class  in
in  are also uniformly bounded, that
are also uniformly bounded, that  is Lebesgue-measurable with
is Lebesgue-measurable with  , and consider a switching rule
, and consider a switching rule  which generates
which generates  , with
, with  defined by the class
defined by the class  of primary self-maps from
of primary self-maps from  to
to  satisfying either
satisfying either

for some sufficiently large  or the Condition
or the Condition  of Section 2 for large contractions, together with the (asymptotic) modified condition
of Section 2 for large contractions, together with the (asymptotic) modified condition 

Then,  has a fixed point.
has a fixed point.
Remark 3.4.
The results of Sections 2 and 3 are extendable directly to the discrete case for the sets  and
and  by replacing Lebesgue measures with discrete ones.
by replacing Lebesgue measures with discrete ones.
Example 3.5.
Fixed point theory is a useful tool to investigate the stability of dynamic systems including standard linear continuous-time or discrete systems and time-delay systems [2, 6] as well as hybrid dynamic systems including coupled continuous-time and discrete-time subsystems [1]. Now, it is discussed the case of a delay-free continuous-time system under a switching rule operating among a given set of parameterizations and subject to controlled and uncontrolled impulses. Consider the linear dynamic unforced time-varying system:

where  and
and  , which are not required to be disjoint, are the real sequences of impulsive time instants where feedback control impulses and open-loop (i.e., feedback-free) control impulses occur, respectively, with the control Dirac distributions being
, which are not required to be disjoint, are the real sequences of impulsive time instants where feedback control impulses and open-loop (i.e., feedback-free) control impulses occur, respectively, with the control Dirac distributions being  and
and  , respectively, of respective piecewise-constant function matrices of dynamics
, respectively, of respective piecewise-constant function matrices of dynamics  and control matrix functions
and control matrix functions  and
and  being run by a switching rule
being run by a switching rule  , for all
, for all  , for all
, for all where ST is the strictly ordered sequence of switching time instants. The real impulsive amplitude sequences
where ST is the strictly ordered sequence of switching time instants. The real impulsive amplitude sequences  and
and  of elements in
of elements in  are assumed to be uniformly bounded and can be finite or infinite. An empty or nonempty sequence of impulsive time instants can occur as follows for some
are assumed to be uniformly bounded and can be finite or infinite. An empty or nonempty sequence of impulsive time instants can occur as follows for some  :
:

either within any simply connected time interval  , where
, where  are two consecutive switching points, or within any interval
are two consecutive switching points, or within any interval  if the switching rule
if the switching rule  generates a finite sequence ST of switching time instants of last element
generates a finite sequence ST of switching time instants of last element  . The following impulsive constraints are assumed.
. The following impulsive constraints are assumed.
(1) such that
such that  for any two consecutive impulsive time instants
for any two consecutive impulsive time instants  , if any, within
, if any, within  with
with  being any two consecutive switching time instants. Also,
being any two consecutive switching time instants. Also,  such that
such that  for any two consecutive switching time instants. The interpretation is that there is no accumulation point either of switching time instants or of impulsive time instants.
for any two consecutive switching time instants. The interpretation is that there is no accumulation point either of switching time instants or of impulsive time instants.
(2)If  then
then  and if
and if  , then
, then 
(3)If  then there is no
then there is no  and
and 
(4)If  and
and  then there is no
then there is no 
(5)If  is of finite Lebesgue measure, then
is of finite Lebesgue measure, then  (i.e., there is at most a finite number of impulsive instants in any finite time interval within two consecutive switching instants).
(i.e., there is at most a finite number of impulsive instants in any finite time interval within two consecutive switching instants).
(6)If there is a finite number of switches generated by the switching law  , so that a finite
, so that a finite is the last one, with
is the last one, with  being of infinite Lebesgue measure then
being of infinite Lebesgue measure then  (i.e., an infinite or finite number of impulsive instants can occur within an infinite time interval).
(i.e., an infinite or finite number of impulsive instants can occur within an infinite time interval).
(7)If  then
then  is of infinity Lebesgue measure so that
is of infinity Lebesgue measure so that  .
.
The unique state trajectory solution of this dynamic system satisfies

where  and
and  is the
is the  th identity matrix. One gets by applying the above relations recursively for the sequence of tie instants
th identity matrix. One gets by applying the above relations recursively for the sequence of tie instants 

so that

with

where  and
and  is the numerical radius
is the numerical radius  (or 2-matrix measure with respect to the spectral
(or 2-matrix measure with respect to the spectral  -norm) of
-norm) of  and the fundamental matrix function is upper-bounded as follows
and the fundamental matrix function is upper-bounded as follows  for any
for any  and some real constants
and some real constants  and
and  , for all
, for all . Then,
. Then,

If  is the last switching time instant, then
is the last switching time instant, then  and
and

and furthermore,

Also, one gets for any finite  , any
, any  , for all
, for all

where  is defined directly from the above expression, provided that there is at least one switching time instant within
is defined directly from the above expression, provided that there is at least one switching time instant within  , where
, where

The case that there is no impulse but one switch within  is included in the above formula by removing the norms
is included in the above formula by removing the norms  since the involved
since the involved  are zero. The case of no switch-no impulse occurring in
are zero. The case of no switch-no impulse occurring in  is also particular case of the above formula (3.19) resulting to be for
is also particular case of the above formula (3.19) resulting to be for 

It follows directly from recursion in (3.21) that for any switching rule  if there exists a
if there exists a  such that
such that 

so that the state-trajectory solution possesses a fixed point exists since

It turns out that if there is at least one stability matrix  , then there are always switching rules
, then there are always switching rules  which lead to a state-trajectory solution possessing a fixed point. Since
which lead to a state-trajectory solution possessing a fixed point. Since  , since
, since  , for any sufficiently large residence interval
, for any sufficiently large residence interval  such that
such that  (i.e., for a sufficiently large time interval free of switches and impulses previous to the next switch after each switch to the stability matrix
(i.e., for a sufficiently large time interval free of switches and impulses previous to the next switch after each switch to the stability matrix  has happened), then the associated map for this switching is asymptotically strictly contractive. They can occur also switches to nonexpansive (
has happened), then the associated map for this switching is asymptotically strictly contractive. They can occur also switches to nonexpansive ( ) or expansive (
) or expansive ( ) generated by the switching rule but a fixed point always exists for such a rule if for some
) generated by the switching rule but a fixed point always exists for such a rule if for some  , there is a dominance of the switching intervals associated with
, there is a dominance of the switching intervals associated with  so that
so that  . In the presence of impulses, the result is still valid by increasing, if necessary, the residence interval before to the next switch after switches to the parameterizing matrix
. In the presence of impulses, the result is still valid by increasing, if necessary, the residence interval before to the next switch after switches to the parameterizing matrix  have happened. It is possible to achieve a constant
have happened. It is possible to achieve a constant  for some
for some  since the norm upper-bounding real function of time
since the norm upper-bounding real function of time  is monotone strictly decreasing related to the residence interval
is monotone strictly decreasing related to the residence interval  .
.
Remark 3.6.
It is important to point out that it is obvious that the generalization of the given formalism to switching rules  is direct; that is the codomain
is direct; that is the codomain  of
of  coincides with the image of
coincides with the image of  so that infinitely many distinct primary self-maps are used to construct
so that infinitely many distinct primary self-maps are used to construct  . This implies necessarily that the switching rule generates infinitely many switches so that the discrete measure of ST is infinity.
. This implies necessarily that the switching rule generates infinitely many switches so that the discrete measure of ST is infinity.
References
De la Sen M: Total stability properties based on fixed point theory for a class of hybrid dynamic systems. Fixed Point Theory and Applications 2009, Article ID 826438 2009:-19.Pages
De la Sen M: About robust stability of dynamic systems with time delays through fixed point theory. Fixed Point Theory and Applications 2008, Article ID 480187 2008:-20.Pages
de la Sen M, Ibeas A: Stability results for switched linear systems with constant discrete delays. Mathematical Problems in Engineering 2008, 2008:-28 Pages.
De la Sen M, Ibeas A: Stability results of a class of hybrid systems under switched continuous-time and discrete-time control. Discrete Dynamics in Nature and Society 2009, Article ID 315713 2009:-28 Pages.
de la Sen M, Ibeas A: On the global asymptotic stability of switched linear time-varying systems with constant point delays. Discrete Dynamics in Nature and Society 2008, Article ID 231710 2008:-31 Pages.
Burton TA: Stability by Fixed Point Theory for Functional Differential Equations. Dover Publications, Mineola, NY, USA; 2006:xiv+348.
Dutta PN, Choudhury BinayakS: A generalisation of contraction principle in metric spaces. Fixed Point Theory and Applications 2008, Article ID 406368 2008:-8 Pages.
Edelstein M: On fixed and periodic points under contractive mappings. Journal of the London Mathematical Society. Second Series 1962, 37: 74–79. 10.1112/jlms/s1-37.1.74
Meir A, Keeler E: A theorem on contraction mappings. Journal of Mathematical Analysis and Applications 1969, 28: 326–329. 10.1016/0022-247X(69)90031-6
Suzuki T: A new type of fixed point theorem in metric spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(11):5313–5317. 10.1016/j.na.2009.04.017
Chen C, Zhu C: Fixed point theorems for times reasonable expansive mapping. Fixed Point Theory and Applications 2008, Article ID 302617 2008:-6 Pages.
Aoyama K, Kimura Y, Takahashi W, Toyoda M: Approximation of common fixed points of a countable family of nonexpansive mappings in a Banach space. Nonlinear Analysis: Theory, Methods & Applications 2007,67(8):2350–2360. 10.1016/j.na.2006.08.032
Hao Y: Convergence theorems of common fixed points for pseudocontractive mappings. Fixed Point Theory and Applications 2008, Article ID 902985 2008:-9 Pages.
Agarwal RP, O'Regan D: Fixed point theory for admissible type maps with applications. Fixed Point Theory and Applications 2009, 2009:-22 Pages.
Olatinwo MO: Some common fixed point theorems for selfmappings satisfying two contractive conditions of integral type in a uniform space. Central European Journal of Mathematics 2008,6(2):335–341. 10.2478/s11533-008-0023-y
Granas A, Dugundji J: Fixed Point Theory, Springer Monographs in Mathematics. Springer, New York, NY, USA; 2003:xvi+690.
Acknowledgments
The author is grateful to the Spanish Ministry of Education by its partial support of this work through Grant DPI2009-07197. He is also grateful to the Basque Government by its support through Grants GIC07143-IT-269-07 and SAIOTEK S-PE08UN15. He is also grateful to the reviewers for their interesting comments which have been very useful to him in order to improve the previous version of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
De la Sen, M. Some Fixed Point Properties of Self-Maps Constructed by Switched Sets of Primary Self-Maps on Normed Linear Spaces. Fixed Point Theory Appl 2010, 438614 (2010). https://doi.org/10.1155/2010/438614
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/438614
 , a subset of
, a subset of  , is the state space of a continuous-time linear time-varying unforced dynamic system described for
, is the state space of a continuous-time linear time-varying unforced dynamic system described for  by
by 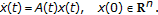
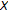 , a subset of
, a subset of  , is the state space of a discrete-time linear time-varying unforced dynamic system described for
, is the state space of a discrete-time linear time-varying unforced dynamic system described for  by
by 
 of strictly contractive primary self-maps from
of strictly contractive primary self-maps from  to
to 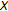 is defined as follows.
is defined as follows.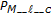 ofnonstrictly contractive large-contractive primary self-maps from
ofnonstrictly contractive large-contractive primary self-maps from 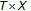 to
to 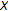 is now defined as follows.
is now defined as follows.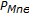 of noncontractive nonexpansive primary self-maps from
of noncontractive nonexpansive primary self-maps from  to
to  is defined as follows.
is defined as follows. of expansive upper-bounded primary self-maps from
of expansive upper-bounded primary self-maps from 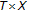 to
to 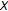 satisfying a global Lipschitz condition and an additional bounding property is now defined as follows.
satisfying a global Lipschitz condition and an additional bounding property is now defined as follows. of neither nonexpansive nor expansive primary self-maps from
of neither nonexpansive nor expansive primary self-maps from 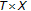 to
to 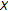 satisfying a global Lipschitz condition is defined in the sequel. This class includes, for instance, primary self-maps which are expansive and globally Lipschitzian and nonexpansive over alternate subsets of
satisfying a global Lipschitz condition is defined in the sequel. This class includes, for instance, primary self-maps which are expansive and globally Lipschitzian and nonexpansive over alternate subsets of  of finite measure and primary functions which are, for instance, asymptotically nonexpansive while being expansive for proper (then finite) subsets
of finite measure and primary functions which are, for instance, asymptotically nonexpansive while being expansive for proper (then finite) subsets  .
.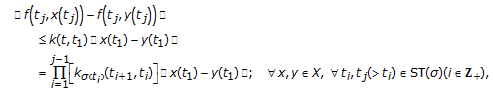
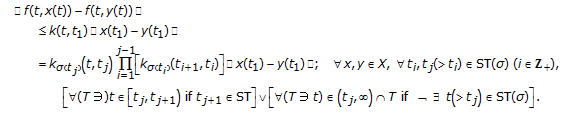
 (finite) does not hold. Since
(finite) does not hold. Since 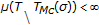 and
and  , there exists a finite
, there exists a finite 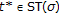 such that
such that  for
for 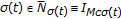 ; for all
; for all 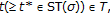 and for
and for 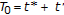 (some finite
(some finite  ), it follows by complete induction that
), it follows by complete induction that 
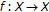 is a large contraction, the real sequence below
is a large contraction, the real sequence below 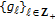 is bounded monotonically strictly decreasing for any pair
is bounded monotonically strictly decreasing for any pair 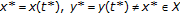 since
since 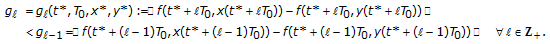
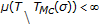 ,
,  . Since
. Since  is uniformly bounded piecewise-continuous since all the functions in
is uniformly bounded piecewise-continuous since all the functions in 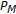 are also uniformly bounded, the corresponding rate over-bounding functions
are also uniformly bounded, the corresponding rate over-bounding functions 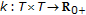 are also uniformly bounded. Then, since
are also uniformly bounded. Then, since 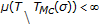 , then the following situations can occur.
, then the following situations can occur.