- Research Article
- Open access
- Published:
An Ishikawa-Hybrid Proximal Point Algorithm for Nonlinear Set-Valued Inclusions Problem Based on  -Accretive Framework
-Accretive Framework
Fixed Point Theory and Applications volume 2010, Article number: 501293 (2010)
Abstract
A general nonlinear framework for an Ishikawa-hybrid proximal point algorithm using the notion of  -accretive is developed. Convergence analysis for the algorithm of solving a nonlinear set-valued inclusions problem and existence analysis of solution for the nonlinear set-valued inclusions problem are explored along with some results on the resolvent operator corresponding to
-accretive is developed. Convergence analysis for the algorithm of solving a nonlinear set-valued inclusions problem and existence analysis of solution for the nonlinear set-valued inclusions problem are explored along with some results on the resolvent operator corresponding to  -accretive mapping due to Lan-Cho-Verma in Banach space. The result that sequence
-accretive mapping due to Lan-Cho-Verma in Banach space. The result that sequence  generated by the algorithm converges linearly to a solution of the nonlinear set-valued inclusions problem with the convergence rate
generated by the algorithm converges linearly to a solution of the nonlinear set-valued inclusions problem with the convergence rate  is proved.
is proved.
1. Introduction
The set-valued inclusions problem, which was introduced and studied by Di Bella [1], Huang et al. [2], and Jeong [3], is a useful extension of the mathematics analysis. And the variational inclusion(inequality) is an important context in the set-valued inclusions problem. It provides us with a unified, natural, novel, innovative, and general technique to study a wide class of problems arising in different branches of mathematical and engineering sciences. Various variational inclusions have been intensively studied in recent years. Ding and Luo[4], Verma [5], Huang [6], Fang and Huang [7], Lan et al. [8], Fang et al. [9], and Zhang et al. [10] introduced the concepts of  -subdifferential operators, maximal
-subdifferential operators, maximal  -monotone operators,
-monotone operators,  -monotone operators,
-monotone operators,  -monotone operators,
-monotone operators,  -monotone operators,
-monotone operators,  -accretive mappings,
-accretive mappings,  -monotone operators, and defined resolvent operators associated with them, respectively. Moreover, by using the resolvent operator technique, many authors constructed some approximation algorithms for some nonlinear variational inclusions in Hilbert spaces or Banach spaces. Recently, Verma has developed a hybrid version of the Eckstein and Bertsekas [11] proximal point algorithm, introduced the algorithm based on the
-monotone operators, and defined resolvent operators associated with them, respectively. Moreover, by using the resolvent operator technique, many authors constructed some approximation algorithms for some nonlinear variational inclusions in Hilbert spaces or Banach spaces. Recently, Verma has developed a hybrid version of the Eckstein and Bertsekas [11] proximal point algorithm, introduced the algorithm based on the  -maximal monotonicity framework [12], and studied convergence of the algorithm.
-maximal monotonicity framework [12], and studied convergence of the algorithm.
On the other hand, in 2008, Li [13] studied the existence of solutions and the stability of perturbed Ishikawa iterative algorithm for nonlinear mixed quasivariational inclusions involving  -accretive mappings in Banach spaces by using the resolvent operator technique in [14].
-accretive mappings in Banach spaces by using the resolvent operator technique in [14].
Inspired and motivated by recent research work in this field, in this paper, a general nonlinear framework for a Ishikawa-hybrid proximal point algorithm using the notion of  -accretive is developed. Convergence analysis for the algorithm of solving a nonlinear set-valued inclusions problem and existence analysis of solution for the nonlinear set-valued inclusions problem are explored along with some results on the resolvent operator corresponding to
-accretive is developed. Convergence analysis for the algorithm of solving a nonlinear set-valued inclusions problem and existence analysis of solution for the nonlinear set-valued inclusions problem are explored along with some results on the resolvent operator corresponding to  -accretive mapping due to Lan et al. in Banach space. The result that sequence
-accretive mapping due to Lan et al. in Banach space. The result that sequence  generated by the algorithm converges linearly to a solution of the nonlinear set-valued inclusions problem as the convergence rate
generated by the algorithm converges linearly to a solution of the nonlinear set-valued inclusions problem as the convergence rate  is proved.
is proved.
2. Preliminaries
Let  be a real Banach space with dual space
be a real Banach space with dual space  and
and  and let the dual pair between
and let the dual pair between  and
and  ,
,  denote the family of all the nonempty subsets of
denote the family of all the nonempty subsets of  and
and  the family of all nonempty closed bounded subsets of
the family of all nonempty closed bounded subsets of  . The generalized duality mapping
. The generalized duality mapping  is defined by
is defined by

where  is a constant.
is a constant.
The modulus of smoothness of  is the function
is the function  defined by
defined by

A Banach space  is called uniformly smooth if
is called uniformly smooth if

 is called
is called  -uniformly smooth if there exists a constant
-uniformly smooth if there exists a constant  such that
such that

Remark 2.1.
In particular,  is the usual normalized duality mapping, and
is the usual normalized duality mapping, and  (for all
(for all  ). If
). If  is strictly convex [15], or
is strictly convex [15], or  is uniformly smooth Banach space, then
is uniformly smooth Banach space, then  is single valued. In what follows we always denote the single-valued generalized duality mapping by
is single valued. In what follows we always denote the single-valued generalized duality mapping by  in real uniformly smooth Banach space
in real uniformly smooth Banach space  unless otherwise stated.
unless otherwise stated.
Let  ;
;  be single-valued mappings. Let
be single-valued mappings. Let  be a set-valued
be a set-valued  -accretive mapping. We consider nonlinear set-valued mixed variational inclusions problem with
-accretive mapping. We consider nonlinear set-valued mixed variational inclusions problem with -accretive mappings (NSVMVIP).
-accretive mappings (NSVMVIP).
For any  , finding
, finding  ,
,  such that
such that

Remark 2.2.
A special case of problem (2.5) is the following.
(i)If  is a Hilbert space,
is a Hilbert space,  is the zero operator in
is the zero operator in  ,
,  is the identity operator in
is the identity operator in  , and
, and  , then problem (2.5) becomes the parametric usual variational inclusion
, then problem (2.5) becomes the parametric usual variational inclusion  with a
with a  -maximal monotone mapping
-maximal monotone mapping  , which was studied by Verma [12].
, which was studied by Verma [12].
(ii)If  is a real Banach space,
is a real Banach space,  is the identity operator in
is the identity operator in  , and
, and  , then problem (2.5) becomes the parametric usual variational inclusion
, then problem (2.5) becomes the parametric usual variational inclusion  with a
with a  -accretive mapping, which was studied by Li [13].
-accretive mapping, which was studied by Li [13].
It is easy to see that a number of known special classes of variational inclusions and variational inequalities in the problem (2.5) are studied (see [2, 7, 12–14]).
Let us recall the following results and concepts.
Definition 2.3.
A single-valued mapping  is said to be
is said to be  -Lipschitz continuous if there exists a constant
-Lipschitz continuous if there exists a constant  such that
such that

Definition 2.4.
A single-valued mapping  is said to be
is said to be
(i)accretive if

(ii)strictly accretive, if  is accretive and
is accretive and  if and only if
if and only if 

 ,
,
(iii) strongly
strongly  -accretive if there exists a constant
-accretive if there exists a constant  such that
such that

(iv) -Lipschitz continuous if there exists a constant
-Lipschitz continuous if there exists a constant  such that
such that

Definition 2.5.
A single-valued mapping  is said to be
is said to be
(i) -Lipschitz continuous if there exist constants
-Lipschitz continuous if there exist constants  such that
such that

(ii) -
- -relaxed cocoercive with respect to
-relaxed cocoercive with respect to  in the first argument if there exist constants
in the first argument if there exist constants  , and
, and  such that
such that

where  are single-valued mappings.
are single-valued mappings.
Definition 2.6.
Let  , and let
, and let  be single-valued mappings. A set-valued mapping
be single-valued mappings. A set-valued mapping  is said to be
is said to be
(i)accretive if

(ii) -accretive if
-accretive if

(iii) -strongly accretive if there exists a constant
-strongly accretive if there exists a constant  such that
such that

(iv) -relaxed
-relaxed  -accretiveif there exists a constant
-accretiveif there exists a constant  such that
such that

(v) -accretive, if
-accretive, if  is accretive and
is accretive and  for all
for all 
(vi) -accretive if
-accretive if  is
is  -relaxed
-relaxed  -accretive and
-accretive and  for all
for all  .
.
Based on the literature [8], we can define the resolvent operator  as follows.
as follows.
Definition 2.7 (see [8]).
Let  be a single-valued mapping,
be a single-valued mapping,  a strictly
a strictly  -accretive single-valued mapping and
-accretive single-valued mapping and  a
a  -accretive mapping. The resolvent operator
-accretive mapping. The resolvent operator  is defined by
is defined by

where  is a constant.
is a constant.
Remark 2.8.
The  -accretive mappings are more general than
-accretive mappings are more general than  -monotone mappings and
-monotone mappings and  -accretive mappings in Banach space or Hilbert space, and the resolvent operators associated with
-accretive mappings in Banach space or Hilbert space, and the resolvent operators associated with  -accretive mappings include as special cases the corresponding resolvent operators associated with
-accretive mappings include as special cases the corresponding resolvent operators associated with  -monotone operators,
-monotone operators,  -accretive mappings,
-accretive mappings,  -monotone operators,
-monotone operators,  -subdifferential operators [3–14, 16, 17].
-subdifferential operators [3–14, 16, 17].
Lemma 2.9 (see [8]).
Let  be
be  -Lipschtiz continuous mapping,
-Lipschtiz continuous mapping,  be an
be an  -strongly
-strongly  -accretive mapping, and
-accretive mapping, and  an
an  -accretive mapping. Then the generalized resolvent operator
-accretive mapping. Then the generalized resolvent operator  is
is  -Lipschitz continuous, that is,
-Lipschitz continuous, that is,

where 
In the study of characteristic inequalities in  -uniformly smooth Banach spaces, Xu [18] proved the following result.
-uniformly smooth Banach spaces, Xu [18] proved the following result.
Lemma 2.10 (see [18]).
Let  be a real uniformly smooth Banach space. Then
be a real uniformly smooth Banach space. Then  is
is  -uniformly smooth if and only if there exists a constant
-uniformly smooth if and only if there exists a constant  such that for all
such that for all  ,
,

3. The Existence of Solutions
Now, we are studing the existence for solutions of problem (2.5).
Lemma 3.1.
Let  be a Banach space. Let
be a Banach space. Let  be a
be a  -Lipschtiz continuous mapping,
-Lipschtiz continuous mapping,  be an
be an  -strongly
-strongly  -accretive mapping, and
-accretive mapping, and  an
an  -accretive mapping. Then the following statements are mutually equivalent.
-accretive mapping. Then the following statements are mutually equivalent.
(i)An element  is a solution of problem (2.5).
is a solution of problem (2.5).
-
(ii)
For a
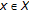 and any
and any 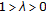 , there exists
, there exists  such that
such that 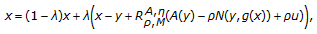 (3.1)
(3.1)
where  is a constant.
is a constant.
Proof.
This directly follows from the definition of  .
.
Theorem 3.2.
Let  be a
be a  -uniformly smooth Banach space. Let
-uniformly smooth Banach space. Let  ;
;  be single-valued mappings, and
be single-valued mappings, and  be a
be a  -Lipschtiz continuous mapping,
-Lipschtiz continuous mapping,  a
a  -strongly
-strongly  -accretive and
-accretive and  -Lipschitz continuous mapping,
-Lipschitz continuous mapping,  be a
be a  -strongly accretive and
-strongly accretive and  -Lipschitz continuous mapping, and
-Lipschitz continuous mapping, and  a
a  -Lipschitz continuous mapping, respectively. Let
-Lipschitz continuous mapping, respectively. Let  be
be  -Lipschitz continuous, and
-Lipschitz continuous, and  -
- -relaxed cocoercive with respect to
-relaxed cocoercive with respect to  in the first argument. Let
in the first argument. Let  be a set-valued
be a set-valued  -accretive mapping. If the following condition holds:
-accretive mapping. If the following condition holds:

where  is the same as in Lemma 2.10, and
is the same as in Lemma 2.10, and  , then the problem (2.5) has a solution
, then the problem (2.5) has a solution  .
.
Proof.
Define a mapping  as follows:
as follows:

For elements  , if we let
, if we let  and
and

then by (3.1), (3.3), and Lemma 2.10, we have

Since  is
is  -
- -relaxed cocoercive with respect to
-relaxed cocoercive with respect to  in the first argument and
in the first argument and  is a
is a  -Lipschitz continuous mapping so we obtain
-Lipschitz continuous mapping so we obtain


By  -strongly accretivity of
-strongly accretivity of  , we have
, we have

Combining(3.5), (3.6), (3.7), and (3.8), we can get

where

It follows from (3.2) and (3.9) that  has a fixed point in
has a fixed point in  , that is, there exists a point
, that is, there exists a point  such that
such that  , and
, and

where  . This completes the proof.
. This completes the proof.
4. Ishikawa-Hybrid Proximal Point Algorithm
Based on Lemma 3.1, we develop an Ishikawa-hybrid proximal point algorithm for finding an iterative sequence solving problem (2.5) as follows.
Algorithm 4.1.
Let
 be a solution of problem ( 2.5 ). Let
be a solution of problem ( 2.5 ). Let
 ,
,
 ,
,
 ,
,
 and
and
 , be five nonnegative sequences such that
, be five nonnegative sequences such that

Step 1.
For an arbitrarily initial point  , we choose suitable
, we choose suitable  , letting
, letting

Step 2.
The sequences  and
and  are generated by an iterative procedure
are generated by an iterative procedure

where 
Remark 4.2.
For a suitable choice of the mappings  , space
, space  , and nonnegative sequences
, and nonnegative sequences  ,
,  , Algorithm 4.1 can be degenerated to a number of algorithms involving many known algorithms which are due to classes of variational inequalities and variational inclusions [12–14].
, Algorithm 4.1 can be degenerated to a number of algorithms involving many known algorithms which are due to classes of variational inequalities and variational inclusions [12–14].
Theorem 4.3.
Let  be the same as in Theorem 3.2, then condition (3.2) holds. Let
be the same as in Theorem 3.2, then condition (3.2) holds. Let  ,
,  ,
,  ,
,  and
and  be the same as in Algorithm 4.1. Then the sequence
be the same as in Algorithm 4.1. Then the sequence  generated by hybrid proximal point Algorithm 4.1 converges linearly to a solution
generated by hybrid proximal point Algorithm 4.1 converges linearly to a solution  of problem (2.5) as
of problem (2.5) as

where  is the same as in Lemma 2.10,
is the same as in Lemma 2.10,  , and the convergence rate is
, and the convergence rate is

Proof.
Suppose that the sequence  is the the sequence generated by the Ishikawa-hybrid proximal point Algorithm 4.1, and that
is the the sequence generated by the Ishikawa-hybrid proximal point Algorithm 4.1, and that  is a solution of problem (2.5). From Lemma 3.1 and condition
is a solution of problem (2.5). From Lemma 3.1 and condition  , we can get
, we can get

where  .
.
For all  , and
, and  , setting
, setting

we find the estimation

By the conditions and Lemma 2.10, we have


It follows from (4.8)–(4.10) that

where


Since  and (4.3),
and (4.3),  and
and

Next, we calculate

This implies that

letting

For all  , set
, set

For the same reason,

where


Furthermore,

Combining (4.16)-(4.22), then we have

By (4.4) and the condition  , we can see that
, we can see that

and the convergence rate is  .By (4.4), if
.By (4.4), if  , then it follows that
, then it follows that  and
and  . Therefor, the sequence
. Therefor, the sequence  generated hybrid proximal point Algorithm 4.1 converges linearly to a solution
generated hybrid proximal point Algorithm 4.1 converges linearly to a solution  of problem (2.5) with convergence rate
of problem (2.5) with convergence rate  . This completes the proof.
. This completes the proof.
Remark 4.4.
For a suitable choice of the mappings  , we can obtain several known results [12–14, 17] as special cases of Theorem 3.2 and Theorem 4.3.
, we can obtain several known results [12–14, 17] as special cases of Theorem 3.2 and Theorem 4.3.
References
Di Bella B: An existence theorem for a class of inclusions. Applied Mathematics Letters 2000,13(3):15–19. 10.1016/S0893-9659(99)00179-2
Huang NJ, Tang YY, Liu YP: Some new existence theorems for nonlinear inclusion with an application. Nonlinear Functional Analysis and Applications 2001,6(3):341–350.
Jeong JU: Generalized set-valued variational inclusions and resolvent equations in Banach spaces. Computers & Mathematics with Applications 2004,47(8–9):1241–1247. 10.1016/S0898-1221(04)90118-6
Ding XP, Luo CL: Perturbed proximal point algorithms for general quasi-variational-like inclusions. Journal of Computational and Applied Mathematics 2000,113(1–2):153–165. 10.1016/S0377-0427(99)00250-2
Verma RU: Approximation-solvability of a class of A-monotone variational inclusion problems. Journal KSIAM 2004,8(1):55–66.
Huang NJ: Nonlinear implicit quasi-variational inclusions involving generalized m -accretive mappings. Archives of Inequalities and Applications 2004,2(4):413–425.
Fang YP, Huang NJ: H -accretive operators and resolvent operator technique for solving variational inclusions in Banach spaces. Applied Mathematics Letters 2004,17(6):647–653. 10.1016/S0893-9659(04)90099-7
Lan HY, Cho YJ, Verma RU: Nonlinear relaxed cocoercive variational inclusions involving
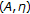 -accretive mappings in Banach spaces. Computers & Mathematics with Applications 2006,51(9–10):1529–1538. 10.1016/j.camwa.2005.11.036
-accretive mappings in Banach spaces. Computers & Mathematics with Applications 2006,51(9–10):1529–1538. 10.1016/j.camwa.2005.11.036Fang YP, Huang NJ, Thompson HB: A new system of variational inclusions with
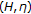 -monotone operators in Hilbert spaces. Computers & Mathematics with Applications. An International Journal 2005,49(2–3):365–374. 10.1016/j.camwa.2004.04.037
-monotone operators in Hilbert spaces. Computers & Mathematics with Applications. An International Journal 2005,49(2–3):365–374. 10.1016/j.camwa.2004.04.037Zhang QB, Zhanging XP, Cheng CZ: Resolvent operator technique for solving generalized implicit variational-like inclusions in Banach space. Journal of Mathematical Analysis and Applications 2007, (20):216–221.
Eckstein J, Bertsekas DP: On the Douglas-Rachford splitting method and the proximal point algorithm for maximal monotone operators. Mathematical Programming 1992,55(3):293–318. 10.1007/BF01581204
Verma RU: A hybrid proximal point algorithm based on the
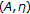 -maximal monotonicity framework. Applied Mathematics Letters 2008,21(2):142–147. 10.1016/j.aml.2007.02.017
-maximal monotonicity framework. Applied Mathematics Letters 2008,21(2):142–147. 10.1016/j.aml.2007.02.017Li HG: Perturbed Ishikawa iterative algorithm and stability for nonlinear mixed quasi-variational inclusions involving
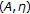 -accretive mappings. Advances in Nonlinear Variational Inequalities 2008,11(1):41–50.
-accretive mappings. Advances in Nonlinear Variational Inequalities 2008,11(1):41–50.Huang NJ, Fang YP: Generalized m -accretive mappings in Banach spaces. Journal of Sichuan University 2001,38(4):591–592.
Weng XL: Fixed point iteration for local strictly pseudo-contractive mapping. Proceedings of the American Mathematical Society 1991,113(3):727–731. 10.1090/S0002-9939-1991-1086345-8
Shim SH, Kang SM, Huang NJ, Cho YJ: Perturbed iterative algorithms with errors for completely generalized strongly nonlinear implicit quasivariational inclusions. Journal of Inequalities and Applications 2000,5(4):381–395. 10.1155/S1025583400000205
Agarwal RP, Cho YJ, Huang NJ: Sensitivity analysis for strongly nonlinear quasi-variational inclusions. Applied Mathematics Letters 2000,13(6):19–24. 10.1016/S0893-9659(00)00048-3
Xu HK: Inequalities in Banach spaces with applications. Nonlinear Analysis. Theory, Methods & Applications 1991,16(12):1127–1138. 10.1016/0362-546X(91)90200-K
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, H., Xu, A. & Jin, M. An Ishikawa-Hybrid Proximal Point Algorithm for Nonlinear Set-Valued Inclusions Problem Based on  -Accretive Framework.
Fixed Point Theory Appl 2010, 501293 (2010). https://doi.org/10.1155/2010/501293
-Accretive Framework.
Fixed Point Theory Appl 2010, 501293 (2010). https://doi.org/10.1155/2010/501293
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/501293
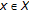 and any
and any 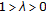 , there exists
, there exists  such that
such that 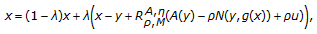
 -accretive mappings in Banach spaces. Computers & Mathematics with Applications 2006,51(9–10):1529–1538. 10.1016/j.camwa.2005.11.036
-accretive mappings in Banach spaces. Computers & Mathematics with Applications 2006,51(9–10):1529–1538. 10.1016/j.camwa.2005.11.036 -monotone operators in Hilbert spaces. Computers & Mathematics with Applications. An International Journal 2005,49(2–3):365–374. 10.1016/j.camwa.2004.04.037
-monotone operators in Hilbert spaces. Computers & Mathematics with Applications. An International Journal 2005,49(2–3):365–374. 10.1016/j.camwa.2004.04.037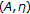 -maximal monotonicity framework. Applied Mathematics Letters 2008,21(2):142–147. 10.1016/j.aml.2007.02.017
-maximal monotonicity framework. Applied Mathematics Letters 2008,21(2):142–147. 10.1016/j.aml.2007.02.017 -accretive mappings. Advances in Nonlinear Variational Inequalities 2008,11(1):41–50.
-accretive mappings. Advances in Nonlinear Variational Inequalities 2008,11(1):41–50.