- Research Article
- Open access
- Published:
Does Kirk's Theorem Hold for Multivalued Nonexpansive Mappings?
Fixed Point Theory and Applications volume 2010, Article number: 546761 (2010)
Abstract
Fixed Point Theory for multivalued mappings has many useful applications in Applied Sciences, in particular, in Game Theory and Mathematical Economics. Thus, it is natural to try of extending the known fixed point results for single-valued mappings to the setting of multivalued mappings. Some theorems of existence of fixed points of single-valued mappings have already been extended to the multivalued case. However, many other questions remain still open, for instance, the possibility of extending the well-known Kirk's Theorem, that is: do Banach spaces with weak normal structure have the fixed point property (FPP) for multivalued nonexpansive mappings? There are many properties of Banach spaces which imply weak normal structure and consequently the FPP for single-valued mappings (for example, uniform convexity, nearly uniform convexity, uniform smoothness,…). Thus, it is natural to consider the following problem: do these properties also imply the FPP for multivalued mappings? In this way, some partial answers to the problem of extending Kirk's Theorem have appeared, proving that those properties imply the existence of fixed point for multivalued nonexpansive mappings. Here we present the main known results and current research directions in this subject. This paper can be considered as a survey, but some new results are also shown.
1. Introduction
The presence or absence of a fixed point (i.e., a point which remains invariant under a map) is an intrinsic property of a map. However, many necessary or sufficient conditions for the existence of such points involve a mixture of algebraic, topological, or metric properties of the mapping or its domain. By Metric Fixed Point Theory, we understand the branch of Fixed Point Theory concerning those results which depend on a metric and which are not preserved when this metric is replaced by another equivalent metric. The first metric fixed point theorem was given by Banach in 1922.
Theorem 1.1 (Banach Contraction Principle, [1]).
Let  be a complete metric space and
be a complete metric space and  a contractive mapping, that is, there exists
a contractive mapping, that is, there exists  such that
such that  for every
for every  . Then
. Then  has a (unique) fixed point
has a (unique) fixed point  . Moreover,
. Moreover,  for every
for every  .
.
Banach Theorem is a basic tool in Functional Analysis, Nonlinear Analysis and Differential Equations. Thus, it is natural to look for some generalizations under weaker assumptions.
For many years Metric Fixed Point Theory just studied some extensions of Banach Theorem relaxing the contractiveness condition, and the extension of this result for multivalued mappings. In the 1960s, Metric Fixed Point Theory received a strong boost when Kirk [2] proved that every (singlevalued) nonexpansive mapping  , defined from a convex closed bounded subset
, defined from a convex closed bounded subset  of a reflexive Banach space with normal structure, has a fixed point.
of a reflexive Banach space with normal structure, has a fixed point.
The celebrated Kirk's theorem had a profound impact in the development of Fixed Point Theory and iniciated the search of more general conditions for a Banach space and for a subset  which assure the existence of fixed points.
which assure the existence of fixed points.
The result obtained by Kirk is, in some sense, surprising because it uses geometric properties of Banach spaces (commonly used in Linear Functional Analysis, but rarely considered in Nonlinear Analysis until then). Thus, it is the starting point for a new mathematical field: the application of the Geometric Theory of Banach Spaces to Fixed Point Theory. From that moment on, many researchers have tried to exploit this connection, essentially considering some other geometric properties of Banach spaces which can be applied to prove the existence of fixed points for different types of nonlinear operators (e.g., uniform smoothness, Opial property, nearly uniform convexity, nearly uniform smoothness, etc.).
Fixed Point Theory for multivalued mappings has useful applications in Applied Sciences, in particular, in Game Theory and Mathematical Economics. Thus, it is natural to study the problem of the extension of the known fixed point results for singlevalued mappings to the setting of multivalued mappings.
Some theorems of existence of fixed points of single-valued mappings have already been extended to the multivalued case. For example, in 1969 Nadler [3] extended the Banach Contraction Principle to multivalued contractive mappings in complete metric spaces. However, many other questions remain open, for instance, the possibility of extending the well-known Kirk's Theorem [2], that is, do Banach spaces with weak normal structure have the fixed point property (FPP) for multivalued nonexpansive mappings?
There are many properties of Banach spaces which imply weak normal structure and consequently the FPP for singlevalued mappings (e.g., uniform convexity, nearly uniform convexity, uniform smoothness, …). Thus, it is natural to consider the following problem: Do these properties also imply the FPP for multivalued mappings? As a consequence, some partial answers to the problem of extending Kirk's Theorem have appeared, which are directed to prove that those properties imply the existence of fixed point for multivalued nonexpansive mappings.
Here we present the main known results and current research directions in this subject. This paper can be considered as a survey, but some new results are also included.
2. Preliminaries
In this section we recall the notion of normal structure and some properties of Banach spaces which imply normal structure.
Normal structure plays an essential role in some problems of Metric Fixed Point Theory, especially those concerning nonexpansive mappings. The notion of normal structure was introduced by Brodskiĭ and Mil'man [4] in 1948 in order to study fixed points of isometries. Later, the notion of normal structure was generalized for the weak topology.
Definition 2.1.
A Banach space  is said to have normal structure (NS) (resp., weak normal structure (
is said to have normal structure (NS) (resp., weak normal structure ( -NS)) if for every bounded closed (resp., weakly compact) convex subset
-NS)) if for every bounded closed (resp., weakly compact) convex subset  of
of  with
with  there exists
there exists  such that
such that  .
.
In 1965 Kirk [2] obtained a strong connection between normal structure and the FPP for nonexpansive mappings.
Theorem 2.2.
Let  be a bounded closed (resp., weakly compact) convex subset of a Banach space
be a bounded closed (resp., weakly compact) convex subset of a Banach space  and let
and let  be a nonexpansive mapping (i.e.,
be a nonexpansive mapping (i.e.,  for every
for every  ). If
). If  is a reflexive Banach space with normal structure (resp., a Banach space with
is a reflexive Banach space with normal structure (resp., a Banach space with  -NS), then
-NS), then  has a fixed point.
has a fixed point.
Bynum [5] defined two coefficients related to normal structure and weak normal structure.
Definition 2.3.
The normal structure coefficient of a Banach space  is defined by
is defined by

where  denotes the
denotes the  eter of
eter of  defined by
defined by  and
and  denotes the Chebyshev radius of
denotes the Chebyshev radius of  defined by
defined by  .
.
The weakly convergent sequence coefficient of  is defined by
is defined by

where the infimum is taken over all weakly convergent sequences  which are not norm convergent, where,
which are not norm convergent, where,

denote the asymptotic  eter and radius of
eter and radius of  respectively.
respectively.
We recall that  is said to have uniform normal structure (UNS) (resp., weak uniform normal structure (
is said to have uniform normal structure (UNS) (resp., weak uniform normal structure ( -UNS)) if
-UNS)) if  (resp.,
(resp.,  ). Notice that this is not the common definition of weak uniform normal structure and is often known as Bynum's condition. It is known that if
). Notice that this is not the common definition of weak uniform normal structure and is often known as Bynum's condition. It is known that if  has uniform normal structure, then
has uniform normal structure, then  is reflexive [6].
is reflexive [6].
In the latest fifty years, some geometrical properties implying normal structure have been studied. Here we are going to recall some of these properties and some results which prove that these properties imply the existence of fixed point for multivalued mappings.
First we consider the Opial property. Opial [7] was the first who studied such a property giving applications to Fixed Point Theory. The uniform Opial property was defined in [8] by Prus, and the Opial modulus was introduced in [9] by Lin et al.
Definition 2.4.
We will say that a Banach space  satisfies the Opial property if for every weakly null sequence
satisfies the Opial property if for every weakly null sequence  and every
and every  in
in  we have
we have

We will say that  satisfies the nonstrict Opial property if
satisfies the nonstrict Opial property if

under the same conditions.
The Opial modulus of  is defined for
is defined for  as
as

where the infimum is taken over all  with
with  and all weakly null sequences
and all weakly null sequences  in
in  with
with  .
.
We will say that  satisfies the uniform Opial property if
satisfies the uniform Opial property if  for all
for all  .
.
There are some relationships between the notions of Opial property and normal structure. If  is a Banach space which satisfies the Opial property, then
is a Banach space which satisfies the Opial property, then  has
has  -NS [10]. On the other hand,
-NS [10]. On the other hand,  [9, Theorem
[9, Theorem  ]. Consequently,
]. Consequently,  has
has  -UNS if
-UNS if  .
.
Next we study the uniform convexity of the space, which is another geometrical property related with normal structure. We recall that a Banach space  is uniformly convex (UC) if and only if
is uniformly convex (UC) if and only if

for each  , or equivalently
, or equivalently

The Clarkson modulus  and the coefficient of normal structure
and the coefficient of normal structure  are related by the following inequality:
are related by the following inequality:  . Consequently, the condition
. Consequently, the condition  implies that
implies that  is reflexive and has uniform normal structure. In particular, notice that not only do uniformly convex spaces have normal structure, but so do all those spaces which do not have segments of length greater than or equal to
is reflexive and has uniform normal structure. In particular, notice that not only do uniformly convex spaces have normal structure, but so do all those spaces which do not have segments of length greater than or equal to  near the unit sphere.
near the unit sphere.
In 1980 Huff [11] initiated the study of nearly uniform convexity which is an infinite-dimensional generalization of uniform convexity. Independently of Huff, Goebel and Sękowski [12] also introduced a property which is equivalent to nearly uniform convexity under the name of noncompact uniform convexity. It is known that a Banach space  is nearly uniformly convex (NUC) if and only if
is nearly uniformly convex (NUC) if and only if

for each  , or equivalently
, or equivalently

where  is a measure of noncompactness. Also we are going to use the following equivalent definition:
is a measure of noncompactness. Also we are going to use the following equivalent definition:  is NUC if and only if
is NUC if and only if  is reflexive and
is reflexive and

for each  , or equivalently
, or equivalently

When  is a reflexive Banach space,
is a reflexive Banach space,  is the separation measure and
is the separation measure and  is the Hausdorff measure (for definitions see, for instance, [13] or [14]), we have the following relationships among the different moduli:
is the Hausdorff measure (for definitions see, for instance, [13] or [14]), we have the following relationships among the different moduli:

and consequently,

If the space  satisfies the nonstrict Opial property, then
satisfies the nonstrict Opial property, then  coincides with
coincides with  .
.
On the other hand, if  (in particular, if
(in particular, if  is NUC), then
is NUC), then  is reflexive and has weak uniform normal structure (see [13, page 125]).
is reflexive and has weak uniform normal structure (see [13, page 125]).
The dual concept of uniform convexity is uniform smoothness which is also related to normal structure. A Banach space  is said to be uniformly smooth (US) if
is said to be uniformly smooth (US) if

where  is the modulus of smoothness of
is the modulus of smoothness of  , defined by
, defined by

for  .
.
It is known that  implies that
implies that  is reflexive and has uniform normal structure [15–17]. However, the infinite-dimensional generalization of uniform smoothness, nearly uniform smoothness, does not imply normal structure [13, Example
is reflexive and has uniform normal structure [15–17]. However, the infinite-dimensional generalization of uniform smoothness, nearly uniform smoothness, does not imply normal structure [13, Example  ].
].
3. Some Properties Implying Weak Normal Structure and the FPP for Multivalued Mappings
In this section we are going to show some results which prove that some properties implying weak normal structure also imply the existence of fixed point for multivalued nonexpansive mappings. As a consequence these results give some partial answers to the problem of extending Kirk's Theorem.
Throughout this section  (resp.,
(resp.,  ) will denote the family of all nonempty compact (resp., compact convex) subsets of
) will denote the family of all nonempty compact (resp., compact convex) subsets of  . We recall that a multivalued mapping
. We recall that a multivalued mapping  is said to be nonexpansive if
is said to be nonexpansive if  for every
for every  , where
, where  denotes the Hausdorff metric given by
denotes the Hausdorff metric given by

for every bounded subsets  and
and  of
of  .
.
In 1973 Lami Dozo gave the following result of existence of fixed point for those spaces which satisfy the Opial property.
Theorem 3.1 (Lami Dozo [18, Theorem  ]).
]).
Let  be a Banach space which satisfies the Opial property, let
be a Banach space which satisfies the Opial property, let  be a weakly compact convex subset of
be a weakly compact convex subset of  and let
and let  be a nonexpansive mapping. Then
be a nonexpansive mapping. Then  has a fixed point, that is, there exists
has a fixed point, that is, there exists  such that
such that  .
.
In 1974 Lim [19] gave a similar result for uniformly convex spaces using Edelstein's method of asymptotic centers [20].
Theorem 3.2 (Lim [19]).
Let  be a uniformly convex Banach space, let
be a uniformly convex Banach space, let  be a closed bounded convex subset of
be a closed bounded convex subset of  and
and  be a nonexpansive mapping. Then
be a nonexpansive mapping. Then  has a fixed point.
has a fixed point.
In 1990 Kirk and Massa proved the following partial generalization of Lim's Theorem using asymptotic centers of sequences and nets. We recall that, given a bounded sequence  in a Banach space
in a Banach space  and a subset
and a subset  of
of  , the asymptotic center of
, the asymptotic center of  with respect to
with respect to  is defined by
is defined by

where  denotes the asymptotic radius of
denotes the asymptotic radius of  with respect to
with respect to  defined by
defined by

Theorem 3.3 (Kirk and Massa [21]).
Let  be a closed bounded convex subset of a Banach space
be a closed bounded convex subset of a Banach space  and
and  a nonexpansive mapping. If the asymptotic center in
a nonexpansive mapping. If the asymptotic center in  of each bounded sequence of
of each bounded sequence of  is nonempty and compact, then
is nonempty and compact, then  has a fixed point.
has a fixed point.
We do not know a complete characterization of those spaces in which asymptotic centers of bounded sequences are compact. Nevertheless, there are some partial answers, for example,  -uniformly convex Banach spaces satisfy that condition [22]. However, an example given by Kuczumov and Prus [23] shows that in nearly uniformly convex spaces, the asymptotic center of a bounded sequence with respect to a closed bounded convex subset is not necessarily compact. Therefore, the problem of obtaining fixed point results in nearly uniformly convex spaces remained open. This question (together with the same question for uniformly smooth spaces) explicitly appeared in a survey about Metric Fixed Point Theory for multivalued mappings published by Xu [24] in 2000.
-uniformly convex Banach spaces satisfy that condition [22]. However, an example given by Kuczumov and Prus [23] shows that in nearly uniformly convex spaces, the asymptotic center of a bounded sequence with respect to a closed bounded convex subset is not necessarily compact. Therefore, the problem of obtaining fixed point results in nearly uniformly convex spaces remained open. This question (together with the same question for uniformly smooth spaces) explicitly appeared in a survey about Metric Fixed Point Theory for multivalued mappings published by Xu [24] in 2000.
The analysis of the importance of the asymptotic center in Kirk-Massa Theorem led Domínguez Benavides and Lorenzo to study some connections between asymptotic centers and the geometry of certain spaces, including nearly uniformly convex spaces. Thus, in [25] Domínguez and Lorenzo obtained the following relationship between the Chebyshev radius of the asymptotic center of a bounded sequence and the modulus of noncompact convexity with respect to the measures  and
and  .
.
Theorem 3.4 (see [25, Theorem  ]).
]).
Let  be a closed convex subset of a reflexive Banach space
be a closed convex subset of a reflexive Banach space  and
and  a bounded sequence in
a bounded sequence in  which is regular with respect to
which is regular with respect to  (i.e., the asymptotic radius is invariant for all subsequences of
(i.e., the asymptotic radius is invariant for all subsequences of  ). Then
). Then

where the Chebyshev radius of a bounded subset  of
of  relative to
relative to  is defined by
is defined by

Moreover, if  satisfies the nonstrict Opial property, then
satisfies the nonstrict Opial property, then

The previous inequalities give an iterative method which reduces at each step the value of the Chebyshev radius for a chain of asymptotic centers. Consequently, Domínguez and Lorenzo deduced in [26] the following partial extension of Kirk's Theorem which, in particular, assures that nearly uniformly convex spaces have the fixed point property for multivalued nonexpansive mappings.
Theorem 3.5 (see [26, Theorem  ]).
]).
Let  be a nonempty closed bounded convex subset of a Banach space
be a nonempty closed bounded convex subset of a Banach space  such that
such that  . Let
. Let  be a nonexpansive mapping. Then
be a nonexpansive mapping. Then  has a fixed point.
has a fixed point.
This result guarantees, in particular, the existence of fixed points in nearly uniformly convex spaces (because  if
if  is NUC), giving a positive answer to one of the previous open problems proposed by Xu.
is NUC), giving a positive answer to one of the previous open problems proposed by Xu.
Dhompongsa et al. [27] observed that the main tool used in the proofs in [25, 26], in order to obtain fixed point results for multivalued nonexpansive mappings, is a relationship between the Chebyshev radius of the asymptotic center of a bounded sequence and the asymptotic radius of the sequence. This relationship also gives an iterative method which reduces at each step the value of the Chebyshev radius for a chain of asymptotic centers. Consequently, in [27, 28] they introduced the Domínguez-Lorenzo condition ((DL)-condition, in short) and property (D) in the following way.
We recall that a sequence  is regular with respect to
is regular with respect to  if
if  for all subsequences
for all subsequences  of
of  , and
, and  is asymptotically uniform with respect to
is asymptotically uniform with respect to  if
if  for all subsequences
for all subsequences  of
of  .
.
Definition 3.6.
A Banach space  is said to satisfy the (DL)-condition if there exists
is said to satisfy the (DL)-condition if there exists  such that for every weakly compact convex subset
such that for every weakly compact convex subset  of
of  and for every bounded sequence
and for every bounded sequence  in
in  which is regular with respect to
which is regular with respect to 

A Banach space  is said to satisfy property (D) if there exists
is said to satisfy property (D) if there exists  such that for any nonempty weakly compact convex subset
such that for any nonempty weakly compact convex subset  of
of  , any bounded sequence
, any bounded sequence  in
in  which is regular and asymptotically uniform with respect to
which is regular and asymptotically uniform with respect to  , and any sequence
, and any sequence  which is regular and asymptotically uniform with respect to
which is regular and asymptotically uniform with respect to  we have
we have

From the definition it is easy to deduce that property (D) is weaker than the (DL)-condition. Dhompongsa et al. proved in [28, Theorem  ] and [28, Theorem
] and [28, Theorem  ] that property (D) implies
] that property (D) implies  -NS and the FPP for multivalued nonexpansive mappings.
-NS and the FPP for multivalued nonexpansive mappings.
Theorem 3.7 (see [28, Theorem  ]).
]).
Let  be a Banach space satisfying property (D). Then
be a Banach space satisfying property (D). Then  has
has  -NS.
-NS.
Theorem 3.8 (see [28, Theorem  ]).
]).
Let  be a nonempty weakly compact convex subset of a Banach space
be a nonempty weakly compact convex subset of a Banach space  which satisfies property (D). Let
which satisfies property (D). Let  be a nonexpansive mapping. Then
be a nonexpansive mapping. Then  has a fixed point.
has a fixed point.
From Theorem 3.5 every Banach space with  satisfies the (DL)-condition. In this paper we present some other properties concerning geometrical constants of Banach spaces which also imply the (DL)-condition or property (D).
satisfies the (DL)-condition. In this paper we present some other properties concerning geometrical constants of Banach spaces which also imply the (DL)-condition or property (D).
Since our goal is to study if properties implying  -NS also imply the FPP for multivalued mappings, a possible approach to that problem is to study if these properties imply either the (DL)-condition or property (D). These results will give only partial answers to the problem of extending Kirk's Theorem for multivalued mappings because we know that uniform normal structure does not imply property (D) ([29, Proposition
-NS also imply the FPP for multivalued mappings, a possible approach to that problem is to study if these properties imply either the (DL)-condition or property (D). These results will give only partial answers to the problem of extending Kirk's Theorem for multivalued mappings because we know that uniform normal structure does not imply property (D) ([29, Proposition  ]); therefore, the problem of extending Kirk's Theorem cannot be fully solved by this approach. In this setting the following results have been obtained.
]); therefore, the problem of extending Kirk's Theorem cannot be fully solved by this approach. In this setting the following results have been obtained.
Theorem 3.9 (Dhompongsa et al. [27, Theorem  ]).
]).
Let  be a uniformly nonsquare Banach space with property WORTH. Then
be a uniformly nonsquare Banach space with property WORTH. Then  satisfies the (DL)-condition.
satisfies the (DL)-condition.
We recall that a Banach space  is uniformly nonsquare if there exists
is uniformly nonsquare if there exists  such that
such that  for every
for every  or equivalently
or equivalently  where
where  denotes the James constant of
denotes the James constant of  defined by
defined by

 is said to satisfy property WORTH if
is said to satisfy property WORTH if

for any  and any weakly null sequence
and any weakly null sequence  in
in  .
.
Theorem 3.10 (Dhompongsa et al. [28, Theorem  ]).
]).
Let  be Banach space such that
be Banach space such that

where  denotes the Jordan-von Neumann constant of
denotes the Jordan-von Neumann constant of  defined by
defined by

Then  satisfies property (D).
satisfies property (D).
Theorem 3.11 (Domínguez Benavides and Gavira [29, Corollary  ]).
]).
Let  be a Banach space such that
be a Banach space such that

Then  satisfies the (DL)-condition. In particular, uniformly smooth Banach spaces (
satisfies the (DL)-condition. In particular, uniformly smooth Banach spaces ( ) satisfy the (DL)-condition.
) satisfy the (DL)-condition.
Theorem 3.12 (Domínguez Benavides and Gavira [29, Corollary  ]).
]).
Let  be a Banach space such that one of the following two equivalent conditions is satisfied
be a Banach space such that one of the following two equivalent conditions is satisfied
(1)
(2) .
.
Then  satisfies the (DL)-condition.
satisfies the (DL)-condition.
Theorem 3.13 (Saejung [30, Theorem  ]).
]).
A Banach space  has property (D) whenever
has property (D) whenever  .
.
This result improves Theorem 3.10 because it is easy to see that  .
.
Theorem 3.14 (Kaewkhao [31, Corollary  ]).
]).
Let  be a Banach space such that
be a Banach space such that

where  denotes the James constant of
denotes the James constant of  defined by
defined by

and  denotes the coefficient of worthwhileness of
denotes the coefficient of worthwhileness of  defined as the infimum of the set of real numbers
defined as the infimum of the set of real numbers  such that
such that

for all  and all weakly null sequences
and all weakly null sequences  in
in  . Then
. Then  satisfies the (DL)-condition.
satisfies the (DL)-condition.
Remark 3.15.
This result improves Theorem 3.9 because if  is a uniformly nonsquare Banach space with property WORTH, then
is a uniformly nonsquare Banach space with property WORTH, then

Theorem 3.16 (Kaewkhao [31, Theorem  ]).
]).
Let  be a Banach space such that
be a Banach space such that

Then  satisfies the (DL)-condition.
satisfies the (DL)-condition.
Theorem 3.17 (Gavira [32, Theorem  ]).
]).
Let  be a Banach space such that
be a Banach space such that

Then  satisfies the (DL)-condition.
satisfies the (DL)-condition.
Remark 3.18 s.
-
(i)
This result is a strict generalization of Theorem 3.16 (see [32]).
-
(ii)
Theorem 3.17 applies to the Bynum space
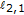 while Theorem 3.11 does not (see [32]). However, we do not know if
while Theorem 3.11 does not (see [32]). However, we do not know if 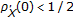 implies
implies 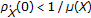 .
.
Finally we show a new result which gives a property implying the (DL)-condition in terms of Clarkson modulus and the García-Falset coefficient.
Theorem 3.19.
Let  be a Banach space such that
be a Banach space such that

where  denotes the García-Falset coefficient of
denotes the García-Falset coefficient of  defined by
defined by

Then  satisfies the (DL)-condition.
satisfies the (DL)-condition.
Proof.
Let  be a nonempty weakly compact convex subset of
be a nonempty weakly compact convex subset of  . Let
. Let  be a bounded sequence in
be a bounded sequence in  which is regular with respect to
which is regular with respect to  . Denote
. Denote  ,
,  and
and  . By translation and multiplication we can assume that
. By translation and multiplication we can assume that  is weakly null and
is weakly null and  . Let
. Let  , then
, then  . Denote
. Denote  by
by  . By the definition of
. By the definition of  we have
we have

For every  there exists
there exists  such that
such that
(1)
(2)
(3)
(4)
Consider  and
and  . Using the above estimates we obtain
. Using the above estimates we obtain

where  tends to 0 as
tends to 0 as  . Furthermore,
. Furthermore,

Also we have

Define  and
and  . Thus,
. Thus,  .
.
Since  for
for  , we obtain
, we obtain

Consequently, we have

Since the last inequality is true for every  and every
and every  , letting
, letting  and using the continuity of
and using the continuity of  , we obtain
, we obtain

In [33] it is proved that  has normal structure under the slightly weaker condition
has normal structure under the slightly weaker condition

It is an open question if this condition implies the (DL)-condition.
Corollary 3.20.
Let  be a uniformly nonsquare Banach space such that
be a uniformly nonsquare Banach space such that  . Then
. Then  satisfies the (DL)-condition.
satisfies the (DL)-condition.
4. Fixed Point Results for Multivalued Nonexpansive Mappings in Modular Function Spaces
The theory of modular spaces was initiated by Nakano [34] in 1950 in connection with the theory of order spaces and redefined and generalized by Musielak and Orlicz [35] in 1959. Even though a metric is not defined, many problems in metric fixed point theory can be reformulated and solved in modular spaces (see, for instance, [36–39]). In particular, Dhompongsa et al. [40] have obtained some fixed point results for multivalued mappings in modular functions spaces.
Let us recall some basic concepts about modular function spaces (for more details the reader is referred to [41, 42]).
Let  be a nonempty set and
be a nonempty set and  a nontrivial
a nontrivial  -algebra of subsets of
-algebra of subsets of  . Let
. Let  be a
be a  -ring of subsets of
-ring of subsets of  , such that
, such that  for any
for any  and
and  . Let us assume that there exists an increasing sequence of sets
. Let us assume that there exists an increasing sequence of sets  such that
such that  (for instance,
(for instance,  can be the class of sets of finite measure in a
can be the class of sets of finite measure in a  -finite measure space). By
-finite measure space). By  we denote the linear space of all simple functions with supports from
we denote the linear space of all simple functions with supports from  . By
. By  we will denote the space of all measurable functions, that is, all functions
we will denote the space of all measurable functions, that is, all functions  such that there exist a sequence
such that there exist a sequence  ,
,  and
and  for all
for all  .
.
Let us recall that a set function  is called a
is called a  -subadditive measure if
-subadditive measure if  ,
,  for any
for any  and
and  for any sequence of sets
for any sequence of sets  . By
. By  we denote the characteristic function of the set
we denote the characteristic function of the set  .
.
Definition 4.1.
A functional  is called a function modular if:
is called a function modular if:
(1) for any
for any  ;
;
(2) whenever
whenever  for any
for any  ,
,  and
and 
(3) is a
is a  -subadditive measure for every
-subadditive measure for every 
(4) as
as  decreases to
decreases to  for every
for every  , where
, where 
(5)if there exists  such that
such that  , then
, then  for every
for every 
(6)for any  ,
,  is order continuous on
is order continuous on  , that is,
, that is,  if
if  and decreases to
and decreases to  .
.
A  -subadditive measure
-subadditive measure  is said to be additive if
is said to be additive if  whenever
whenever  such that
such that  and
and  .
.
The definition of  is then extended to
is then extended to  by
by

Definition 4.2.
A set  is said to be
is said to be  -null if
-null if  for every
for every  . A property
. A property  is said to hold
is said to hold  -almost everywhere (
-almost everywhere ( -a.e.) if the set
-a.e.) if the set  is
is  -null. For example, we will say frequently
-null. For example, we will say frequently 
 -a.e.
-a.e.
Note that a countable union of  -null sets is still
-null sets is still  -null. In the sequel we will identify sets
-null. In the sequel we will identify sets  and
and  whose symmetric difference
whose symmetric difference  is
is  -null, similarly we will identify measurable functions which differ only on a
-null, similarly we will identify measurable functions which differ only on a  -null set.
-null set.
Under the above conditions, we define the function  by
by  . We know from [41] that
. We know from [41] that  satisfies the following properties:
satisfies the following properties:
(i) if and only if
if and only if 
 -a.e.
-a.e.
(ii) for every scalar
for every scalar  with
with  and
and  .
.
(iii) if
if  ,
,  and
and  .
.
In addition, if the following property is satisfied
(iii) if
if  ,
,  and
and  ,
,
we say that  is a convex modular.
is a convex modular.
A function modular  is called
is called  -finite if there exists an increasing sequence of sets
-finite if there exists an increasing sequence of sets  such that
such that  and
and  .
.
The modular  defines a corresponding modular space
defines a corresponding modular space  , which is given by
, which is given by

In general the modular  is not subadditive and therefore does not behave as a norm or a distance. But one can associate to a modular an
is not subadditive and therefore does not behave as a norm or a distance. But one can associate to a modular an  -norm. In fact, when
-norm. In fact, when  is convex, the formula
is convex, the formula

defines a norm which is frequently called the Luxemburg norm. The formula

defines a different norm which is called the Amemiya norm. Moreover,  and
and  are equivalent norms. We can also consider the space
are equivalent norms. We can also consider the space

Definition 4.3.
A function modular  is said to satisfy the
is said to satisfy the  -condition if
-condition if

It is known that the  -condition is equivalent to
-condition is equivalent to  .
.
Definition 4.4.
A function modular  is said to satisfy the
is said to satisfy the  -type condition if there exists
-type condition if there exists  such that for any
such that for any  we have
we have  .
.
In general, the  -type condition and
-type condition and  -condition are not equivalent, even though it is obvious that the
-condition are not equivalent, even though it is obvious that the  -type condition implies the
-type condition implies the  -condition.
-condition.
Definition 4.5.
Let  be a modular space.
be a modular space.
(1)The sequence  is said to be
is said to be  -convergent to
-convergent to  if
if  as
as  .
.
(2)The sequence  is said to be
is said to be  -a.e. convergent to
-a.e. convergent to  if the set
if the set  is
is  -null.
-null.
(3)A subset  of
of  is called
is called  -a.e. closed if the
-a.e. closed if the  -a.e. limit of a
-a.e. limit of a  -a.e. convergent sequence of
-a.e. convergent sequence of  always belongs to
always belongs to  .
.
(4)A subset  of
of  is called
is called  -a.e. compact if every sequence in
-a.e. compact if every sequence in  has a
has a  -a.e. convergent subsequence in
-a.e. convergent subsequence in  .
.
(5)A subset  of
of  is called
is called  -bounded if
-bounded if

We know by [41] that under the  -condition the norm convergence and modular convergence are equivalent, which implies that the norm and modular convergence are also the same when we deal with the
-condition the norm convergence and modular convergence are equivalent, which implies that the norm and modular convergence are also the same when we deal with the  -type condition. In the sequel we will assume that the modular function
-type condition. In the sequel we will assume that the modular function  is convex and satisfies the
is convex and satisfies the  -type condition. Hence, the
-type condition. Hence, the  -convergence defines a topology which is identical to the norm topology.
-convergence defines a topology which is identical to the norm topology.
In the same way as the Hausdorff distance defined on the family of bounded closed subsets of a metric space, we can define the analogue to the Hausdorff distance for modular function spaces. We will speak of  -Hausdorff distance even though it is not a metric.
-Hausdorff distance even though it is not a metric.
Definition 4.6.
Let  be a nonempty subset of
be a nonempty subset of  . We will denote by
. We will denote by  the family of nonempty
the family of nonempty  -closed subsets of
-closed subsets of  and by
and by  the family of nonempty
the family of nonempty  -compact subsets of
-compact subsets of  . Let
. Let  be the
be the  -Hausdorff distance on
-Hausdorff distance on  , that is,
, that is,

where  is the
is the  -distance between
-distance between  and
and  . A multivalued mapping
. A multivalued mapping  is said to be a
is said to be a  -contraction if there exists a constant
-contraction if there exists a constant  such that
such that

If it is valid when  , then
, then  is called
is called  -nonexpansive.
-nonexpansive.
A function  is called a fixed point for a multivalued mapping
is called a fixed point for a multivalued mapping  if
if  .
.
Dhompongsa et al. [40] stated the Banach Contraction Principle for multivalued mappings in modular function spaces.
Theorem 4.7 (see [40, Theorem  ]).
]).
Let  be a convex function modular satisfying the
be a convex function modular satisfying the  -type condition,
-type condition,  a nonempty
a nonempty  -bounded
-bounded  -closed subset of
-closed subset of  , and
, and  a
a  -contraction mapping, that is, there exists a constant
-contraction mapping, that is, there exists a constant  such that
such that

Then  has a fixed point.
has a fixed point.
By using that result, they proved the existence of fixed points for multivalued  -nonexpansive mappings.
-nonexpansive mappings.
Theorem 4.8 (see [40, Theorem  ]).
]).
Let  be a convex function modular satisfying the
be a convex function modular satisfying the  -type condition,
-type condition,  a nonempty
a nonempty  -a.e. compact
-a.e. compact  -bounded convex subset of
-bounded convex subset of  , and
, and  a
a  -nonexpansive mapping. Then
-nonexpansive mapping. Then  has a fixed point.
has a fixed point.
They also applied the above theorem to obtain fixed point results in the Banach space  (resp.,
(resp.,  ) for multivalued mappings whose domains are compact in the topology of the convergence locally in measure (resp.,
) for multivalued mappings whose domains are compact in the topology of the convergence locally in measure (resp.,  -topology).
-topology).
Consider the space  for a
for a  -finite measure
-finite measure  with the usual norm. Let
with the usual norm. Let  be a bounded closed convex subset of
be a bounded closed convex subset of  for
for  and
and  a multivalued nonexpansive mapping. Because of uniform convexity of
a multivalued nonexpansive mapping. Because of uniform convexity of  , it is known that
, it is known that  has a fixed point. For
has a fixed point. For  ,
,  can fail to have a fixed point even in the singlevalued case for a weakly compact convex set
can fail to have a fixed point even in the singlevalued case for a weakly compact convex set  (see [43]). However, since
(see [43]). However, since  is a modular space where
is a modular space where  for all
for all  , Theorem 4.8 implies the existence of a fixed point when we define mappings on a
, Theorem 4.8 implies the existence of a fixed point when we define mappings on a  -a.e. compact
-a.e. compact  -bounded convex subset of
-bounded convex subset of  . Thus the following can be stated.
. Thus the following can be stated.
Corollary 4.9 (see [40, Corollary  ]).
]).
Let  be as above,
be as above,  a nonempty bounded convex set which is compact for the topology of the convergence locally in measure, and
a nonempty bounded convex set which is compact for the topology of the convergence locally in measure, and  a nonexpansive mapping. Then
a nonexpansive mapping. Then  has a fixed point.
has a fixed point.
In the case of the space  we also can obtain a bounded closed convex set
we also can obtain a bounded closed convex set  and a nonexpansive mapping
and a nonexpansive mapping  which is fixed point free. Indeed, consider the following easy and well-known example.
which is fixed point free. Indeed, consider the following easy and well-known example.
Let

Define a nonexpansive mapping  by
by

then  is a fixed point free map. However, if we consider
is a fixed point free map. However, if we consider  where
where  , for all
, for all  , then
, then  -a.e. convergence and
-a.e. convergence and  -convergence are identical on bounded subsets of
-convergence are identical on bounded subsets of  (see [36]). This fact leads to the following corollary.
(see [36]). This fact leads to the following corollary.
Corollary 4.10 (see [40, Corollary  ]).
]).
Let  be a nonempty
be a nonempty  -compact convex subset of
-compact convex subset of  and
and  a nonexpansive mapping. Then
a nonexpansive mapping. Then  has a fixed point.
has a fixed point.
Next we will give a property of closed convex bounded subsets of  more general than weak star compactness which implies the fixed point property for nonexpansive mappings.
more general than weak star compactness which implies the fixed point property for nonexpansive mappings.
Domínguez et al. introduced in [44] some compactness conditions concerning proximinal subsets called Property (P). Following this idea we will use the following similar notion for modular function spaces.
Definition 4.11.
Let  be a nonempty
be a nonempty  -closed convex
-closed convex  -bounded subset of
-bounded subset of  . It is said that
. It is said that  has Property (
has Property ( ) if for every
) if for every  which is the
which is the  -a.e. limit of a sequence in
-a.e. limit of a sequence in  , the set
, the set  is a nonempty and
is a nonempty and  -compact subset of
-compact subset of  , where
, where 
Using that notion and the following two lemmas, we obtain a new fixed point result for multivalued  -nonexpansive mappings.
-nonexpansive mappings.
Lemma 4.12 (see [40, Lemma  ]).
]).
Let  be a convex function modular satisfying the
be a convex function modular satisfying the  -type condition,
-type condition,  , and
, and  a nonempty
a nonempty  -compact subset of
-compact subset of  . Then there exists
. Then there exists  such that
such that

Lemma 4.13 (see [37, Lemma  ]).
]).
Let  be a function modular satisfying the
be a function modular satisfying the  -type condition, and
-type condition, and  be a sequence in
be a sequence in  such that
such that  and there exists
and there exists  such that
such that  . Then,
. Then,

Theorem 4.14.
Let  be a convex function modular satisfying the
be a convex function modular satisfying the  -type condition,
-type condition,  a nonempty
a nonempty  -closed
-closed  -bounded convex subset of
-bounded convex subset of  satisfying Property
satisfying Property  such that every sequence in
such that every sequence in  has a
has a  -a.e. convergent subsequence in
-a.e. convergent subsequence in  , and
, and  a
a  -nonexpansive mapping. Then
-nonexpansive mapping. Then  has a fixed point.
has a fixed point.
Proof.
Fix  . For each
. For each  , the
, the  -contraction
-contraction  is defined by
is defined by

By Theorem 4.7, we can conclude that  has a fixed point, say
has a fixed point, say  . It is easy to see that
. It is easy to see that

By our assumptions, we can assume, by passing through a subsequence, that  for some
for some  . By Lemma 4.12, for each
. By Lemma 4.12, for each  there exists
there exists  such that
such that

Now we are going to show that  for each
for each  . Taking any
. Taking any  , from the
, from the  -compactness of
-compactness of  and Lemma 4.12, we can find
and Lemma 4.12, we can find  such that
such that

and we can assume, by passing through a subsequence, that  for some
for some  . From above and using Lemma 4.13, it follows that
. From above and using Lemma 4.13, it follows that

On the other hand, by Lemma 4.13 we also have

Thus, we deduce  , which implies that
, which implies that  and so
and so  .
.
Now we define the mapping  by
by  . From [45, Proposition
. From [45, Proposition  ] we know that the mapping
] we know that the mapping  is upper semicontinuous. Since
is upper semicontinuous. Since  is a nonempty
is a nonempty  -compact convex set and the
-compact convex set and the  -topology is a norm-topology, we can apply the Kakutani-Bohnenblust-Karlin Theorem (see [14]) to obtain a fixed point for
-topology is a norm-topology, we can apply the Kakutani-Bohnenblust-Karlin Theorem (see [14]) to obtain a fixed point for  and hence for
and hence for  .
.
If we apply the previous theorem in the particular case of the space  for a
for a  -finite measure
-finite measure  with the usual norm, we obtain the following result, which can be also deduced from [44, Theorem
with the usual norm, we obtain the following result, which can be also deduced from [44, Theorem  ].
].
Corollary 4.15.
Let  be as above,
be as above,  a nonempty closed bounded convex set which satisfies Property (P). Suppose, in addition, that every sequence in
a nonempty closed bounded convex set which satisfies Property (P). Suppose, in addition, that every sequence in  has a convergent locally in measure subsequence in
has a convergent locally in measure subsequence in  . If
. If  is a nonexpansive mapping, then
is a nonexpansive mapping, then  has a fixed point.
has a fixed point.
If we consider now the space  , then the assumption of existence of a
, then the assumption of existence of a  -convergent subsequence for every sequence in
-convergent subsequence for every sequence in  can be removed and we can state the following result.
can be removed and we can state the following result.
Corollary 4.16.
Let  be a nonempty closed bounded convex subset of
be a nonempty closed bounded convex subset of  which satisfies Property (P). If
which satisfies Property (P). If  is a nonexpansive mapping, then
is a nonexpansive mapping, then  has a fixed point.
has a fixed point.
Notice that in  there exists a subset with Property (P) which is not
there exists a subset with Property (P) which is not  -compact.
-compact.
Example 4.17 (see [44, Example  ]).
]).
Let  be a bounded sequence of nonnegative real numbers and let
be a bounded sequence of nonnegative real numbers and let  be the standard Schauder basis of
be the standard Schauder basis of  . It is clear that the set
. It is clear that the set  , where
, where  , is never weakly star compact. Nevertheless, by using [46, Example
, is never weakly star compact. Nevertheless, by using [46, Example  ] it is easy to show that
] it is easy to show that  has Property (P) if and only if
has Property (P) if and only if  is nonempty and finite.
is nonempty and finite.
References
Banach S: Sur les opérations dans les ensembles abstraits et leurs applications. Fundamenta Mathematicae 1922, 3: 133–181.
Kirk WA: A fixed point theorem for mappings which do not increase distances. The American Mathematical Monthly 1965, 72: 1004–1006. 10.2307/2313345
Nadler SB Jr.: Multi-valued contraction mappings. Pacific Journal of Mathematics 1969, 30: 475–488.
Brodskiĭ MS, Mil'man DP: On the center of a convex set. Doklady Akademii Nauk SSSR 1948, 59: 837–840.
Bynum WL: Normal structure coefficients for Banach spaces. Pacific Journal of Mathematics 1980,86(2):427–436.
Maluta E: Uniformly normal structure and related coefficients. Pacific Journal of Mathematics 1984,111(2):357–369.
Opial Z: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bulletin of the American Mathematical Society 1967, 73: 591–597. 10.1090/S0002-9904-1967-11761-0
Prus S: Banach spaces with the uniform Opial property. Nonlinear Analysis: Theory, Methods & Applications 1992,18(8):697–704. 10.1016/0362-546X(92)90165-B
Lin P-K, Tan K-K, Xu HK: Demiclosedness principle and asymptotic behavior for asymptotically nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 1995,24(6):929–946. 10.1016/0362-546X(94)00128-5
Gossez J-P, Lami Dozo E: Some geometric properties related to the fixed point theory for nonexpansive mappings. Pacific Journal of Mathematics 1972, 40: 565–573.
Huff R: Banach spaces which are nearly uniformly convex. The Rocky Mountain Journal of Mathematics 1980,10(4):743–749. 10.1216/RMJ-1980-10-4-743
Goebel K, Sękowski T: The modulus of noncompact convexity. Annales Universitatis Mariae Curie-Skłodowska. Sectio A 1984, 38: 41–48.
Ayerbe Toledano JM, Domínguez Benavides T, López Acedo G: Measures of Noncompactness in Metric Fixed Point Theory, Operator Theory: Advances and Applications. Volume 99. Birkhäuser, Basel, Switzerland; 1997:viii+211.
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Turett B: A dual view of a theorem of Baillon. In Nonlinear Analysis and Applications (St. Johns, Nfld., 1981), Lecture Notes in Pure and Applied Mathematics. Volume 80. Marcel Dekker, New York, NY, USA; 1982:279–286.
Khamsi MA: On metric spaces with uniform normal structure. Proceedings of the American Mathematical Society 1989,106(3):723–726. 10.1090/S0002-9939-1989-0972234-4
Prus S: Some estimates for the normal structure coefficient in Banach spaces. Rendiconti del Circolo Matematico di Palermo 1991,40(1):128–135. 10.1007/BF02846365
Lami Dozo E: Multivalued nonexpansive mappings and Opial's condition. Proceedings of the American Mathematical Society 1973, 38: 286–292.
Lim TC: A fixed point theorem for multivalued nonexpansive mappings in a uniformly convex Banach space. Bulletin of the American Mathematical Society 1974, 80: 1123–1126. 10.1090/S0002-9904-1974-13640-2
Edelstein M: The construction of an asymptotic center with a fixed-point property. Bulletin of the American Mathematical Society 1972, 78: 206–208. 10.1090/S0002-9904-1972-12918-5
Kirk WA, Massa S: Remarks on asymptotic and Chebyshev centers. Houston Journal of Mathematics 1990,16(3):357–364.
Kirk WA: Nonexpansive mappings in product spaces, set-valued mappings and -uniform rotundity. In Nonlinear Functional Analysis and Its Applications, Part 2 (Berkeley, Calif., 1983), Proc. Sympos. Pure Math.. Volume 45. American Mathematical Society, Providence, RI, USA; 1986:51–64.
Kuczumow T, Prus S: Compact asymptotic centers and fixed points of multivalued nonexpansive mappings. Houston Journal of Mathematics 1990,16(4):465–468.
Xu H-K: Metric fixed point theory for multivalued mappings. Dissertationes Mathematicae 2000, 389: 39.
Domínguez Benavides T, Lorenzo Ramírez P: Fixed-point theorems for multivalued non-expansive mappings without uniform convexity. Abstract and Applied Analysis 2003,2003(6):375–386. 10.1155/S1085337503203080
Domínguez Benavides T, Lorenzo Ramírez P: Asymptotic centers and fixed points for multivalued nonexpansive mappings. Annales Universitatis Mariae Curie-Skłodowska. Sectio A 2004, 58: 37–45.
Dhompongsa S, Kaewcharoen A, Kaewkhao A: The Domínguez-Lorenzo condition and multivalued nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications and Methods 2006,64(5):958–970. 10.1016/j.na.2005.05.051
Dhompongsa S, Domínguez Benavides T, Kaewcharoen A, Kaewkhao A, Panyanak B: The Jordan-von Neumann constants and fixed points for multivalued nonexpansive mappings. Journal of Mathematical Analysis and Applications 2006,320(2):916–927. 10.1016/j.jmaa.2005.07.063
Domínguez Benavides T, Gavira B: The fixed point property for multivalued nonexpansive mappings. Journal of Mathematical Analysis and Applications 2007,328(2):1471–1483. 10.1016/j.jmaa.2006.06.059
Saejung S: Remarks on sufficient conditions for fixed points of multivalued nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 2007,67(5):1649–1653. 10.1016/j.na.2006.07.037
Kaewkhao A: The James constant, the Jordan-von Neumann constant, weak orthogonality, and fixed points for multivalued mappings. Journal of Mathematical Analysis and Applications 2007,333(2):950–958. 10.1016/j.jmaa.2006.12.001
Gavira B: Some geometric conditions which imply the fixed point property for multivalued nonexpansive mappings. Journal of Mathematical Analysis and Applications 2008,339(1):680–690. 10.1016/j.jmaa.2007.07.015
Jiao H, Guo Y, Wang F: Modulus of convexity, the coefficient
 , and normal structure in Banach spaces. Abstract and Applied Analysis 2008, 2008:-5.
, and normal structure in Banach spaces. Abstract and Applied Analysis 2008, 2008:-5.Nakano H: Modulared Semi-Ordered Linear Spaces. Maruzen, Tokyo, Japan; 1950.
Musielak J, Orlicz W: On modular spaces. Studia Mathematica 1959, 18: 49–65.
Domínguez Benavides T, Khamsi MA, Samadi S: Asymptotically regular mappings in modular function spaces. Scientiae Mathematicae Japonicae 2001,53(2):295–304.
Domínguez Benavides T, Khamsi MA, Samadi S: Asymptotically nonexpansive mappings in modular function spaces. Journal of Mathematical Analysis and Applications 2002,265(2):249–263. 10.1006/jmaa.2000.7275
Khamsi MA: Fixed point theory in modular function spaces. In Recent Advances on Metric Fixed Point Theory (Seville, 1995), Ciencias. Volume 48. Universidad de Sevilla, Seville, Spain; 1996:31–57.
Khamsi MA, Kozłowski WM, Reich S: Fixed point theory in modular function spaces. Nonlinear Analysis: Theory, Methods & Applications 1990,14(11):935–953. 10.1016/0362-546X(90)90111-S
Dhompongsa S, Domínguez Benavides T, Kaewcharoen A, Panyanak B: Fixed point theorems for multivalued mappings in modular function spaces. Scientiae Mathematicae Japonicae 2006,63(2):161–169.
Kozlowski WM: Modular Function Spaces, Monographs and Textbooks in Pure and Applied Mathematics. Volume 122. Marcel Dekker, New York, NY, USA; 1988:x+252.
Musielak J: Orlicz Spaces and Modular Spaces, Lecture Notes in Mathematics. Volume 1034. Springer, Berlin, Germany; 1983:iii+222.
Alspach DE: A fixed point free nonexpansive map. Proceedings of the American Mathematical Society 1981,82(3):423–424. 10.1090/S0002-9939-1981-0612733-0
Domínguez Benavides T, García Falset J, Llorens-Fuster E, Lorenzo Ramírez P: Fixed point properties and proximinality in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(5–6):1562–1571. 10.1016/j.na.2008.12.048
Hu S, Papageorgiou NS: Handbook of Multivalued Analysis. Vol. I. Theory, Mathematics and Its Applications. Volume 419. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1997:xvi+964.
Goebel K, Kuczumov T: Irregular convex sets with fixed point property for nonexpansive mappings. Colloqium Mathematicum 1979, 259–264.
Acknowledgments
The authors are very grateful to the anonymous referee for some useful suggestions to improve the presentation of this paper. This research was partially supported by DGES Grant no.BFM2006-13997-C02-01 and Junta de Andalucía Grant no.FQM-127. This research is dedicated to W. A. Kirk celebrating his wide and deep contribution in Metric Fixed Point Theory.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Domínguez Benavides, T., Gavira, B. Does Kirk's Theorem Hold for Multivalued Nonexpansive Mappings?. Fixed Point Theory Appl 2010, 546761 (2010). https://doi.org/10.1155/2010/546761
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/546761
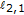 while Theorem 3.11 does not (see [
while Theorem 3.11 does not (see [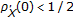 implies
implies 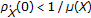 .
. , and normal structure in Banach spaces. Abstract and Applied Analysis 2008, 2008:-5.
, and normal structure in Banach spaces. Abstract and Applied Analysis 2008, 2008:-5.