- Research Article
- Open access
- Published:
Weak Convergence Theorems for a Countable Family of Strict Pseudocontractions in Banach Spaces
Fixed Point Theory and Applications volume 2010, Article number: 632137 (2010)
Abstract
We investigate the convergence of Mann-type iterative scheme for a countable family of strict pseudocontractions in a uniformly convex Banach space with the Fréchet differentiable norm. Our results improve and extend the results obtained by Marino-Xu, Zhou, Osilike-Udomene, Zhang-Guo and the corresponding results. We also point out that the condition given by Chidume-Shahzad (2010) is not satisfied in a real Hilbert space. We show that their results still are true under a new condition.
1. Introduction
Let  and
and  be a real Banach space and the dual space of
be a real Banach space and the dual space of  , respectively. Let
, respectively. Let  be a nonempty subset of
be a nonempty subset of  . Let
. Let  denote the normalized duality mapping from
denote the normalized duality mapping from  into
into  given by
given by  , for all
, for all  , where
, where  denotes the duality pairing between
denotes the duality pairing between  and
and  . If
. If  is smooth or
is smooth or  is strictly convex, then
is strictly convex, then  is single-valued.
is single-valued.
Throughout this paper, we denote the single valued duality mapping by  and denote the set of fixed points of a nonlinear mapping
and denote the set of fixed points of a nonlinear mapping  by
by

Definition 1.1.
A mapping  with domain
with domain  and range
and range  in
in  is called
is called
(i)pseudocontractive [1] if, for all  , there exists
, there exists  such that
such that

(ii) -strictly pseudocontractive [2] if for all
-strictly pseudocontractive [2] if for all  , there exist
, there exist  and
and  such that
such that

or equivalently

(iii)L-Lipschitzian if, for all  , there exists a constant
, there exists a constant  such that
such that

Remark 1.2.
It is obvious by the definition that
(1)every strictly pseudocontractive mapping is pseudocontractive,
(2)every  -strictly pseudocontractive mapping is
-strictly pseudocontractive mapping is  -Lipschitzian; see [3].
-Lipschitzian; see [3].
Remark 1.3.
Let  be a nonempty subset of a real Hilbert space and
be a nonempty subset of a real Hilbert space and  a mapping. Then
a mapping. Then  is said to be
is said to be  -strictly pseudocontractive [2] if, for all
-strictly pseudocontractive [2] if, for all  , there exists
, there exists  such that
such that

It is well know that (1.6) is equivalent to the following:

It is worth mentioning that the class of strict pseudocontractions includes properly the class of nonexpansive mappings. Moreover, we know from [4] that the class of pseudocontractions also includes properly the class of strict pseudocontractions. A mapping  is called accretive if, for all
is called accretive if, for all  , there exists
, there exists  such that
such that  . It is also known that
. It is also known that  is accretive if and only if
is accretive if and only if  is pseudocontractive. Hence, a solution of the equation
is pseudocontractive. Hence, a solution of the equation  is a solution of the fixed point of
is a solution of the fixed point of  . Note that if
. Note that if  , then
, then  is
is  -strictly accretive if and only if
-strictly accretive if and only if  is
is  -strictly pseudocontractive.
-strictly pseudocontractive.
In 1953, Mann [5] introduced the iteration as follows: a sequence  defined by
defined by  and
and

where  . If
. If  is a nonexpansive mapping with a fixed point and the control sequence
is a nonexpansive mapping with a fixed point and the control sequence  is chosen so that
is chosen so that  , then the sequence
, then the sequence  defined by (1.8) converges weakly to a fixed point of
defined by (1.8) converges weakly to a fixed point of  ( this is also valid in a uniformly convex Banach space with the Fréchet differentiable norm [6] ). However, if
( this is also valid in a uniformly convex Banach space with the Fréchet differentiable norm [6] ). However, if  is a Lipschitzian pseudocontractive mapping, then Mann iteration defined by (1.8) may fail to converge in a Hilbert space; see [4].
is a Lipschitzian pseudocontractive mapping, then Mann iteration defined by (1.8) may fail to converge in a Hilbert space; see [4].
In 1967, Browder-Petryshyn [2] introduced the class of strict pseudocontractions and proved existence and weak convergence theorems in a real Hilbert setting by using Mann's iteration (1.8) with a constant sequence  for all
for all  . Respectively, Marino-Xu [7] and Zhou [8] extended the results of Browder-Petryshyn [2] to Mann's iteration process (1.8). To be more precise, they proved the following theorem.
. Respectively, Marino-Xu [7] and Zhou [8] extended the results of Browder-Petryshyn [2] to Mann's iteration process (1.8). To be more precise, they proved the following theorem.
Theorem 1.4 (see [7]).
Let  be a closed convex subset of a real Hilbert space
be a closed convex subset of a real Hilbert space  . Let
. Let  be a
be a  -strict pseudocontraction for some
-strict pseudocontraction for some  , and assume that
, and assume that  admits a fixed point in
admits a fixed point in  . Let a sequence
. Let a sequence  be the sequence generated by Mann's algorithm (1.8). Assume that the control sequence
be the sequence generated by Mann's algorithm (1.8). Assume that the control sequence  is chosen so that
is chosen so that  for all
for all  and
and  . Then
. Then  converges weakly to a fixed point of
converges weakly to a fixed point of  .
.
Meanwhile, Marino, and Xu raised the open question: whether Theorem 1.4 can be extended to Banach spaces which are uniformly convex and have a Fréchet differentiable norm. Later, Zhou [9] and Zhang-Su [10], respectively, extended the result above to  -uniformly smooth and
-uniformly smooth and  -uniformly smooth Banach spaces which are uniformly convex or satisfy Opial's condition.
-uniformly smooth Banach spaces which are uniformly convex or satisfy Opial's condition.
In 2001, Osilike-Udomene [11] proved the convergence theorems of the Mann [5] and Ishikawa [12] iteration methods in the framework of  -uniformly smooth and uniformly convex Banach spaces. They also obtained that a sequence
-uniformly smooth and uniformly convex Banach spaces. They also obtained that a sequence  defined by (1.8) converges weakly to a fixed point of
defined by (1.8) converges weakly to a fixed point of  under suitable control conditions. However, the sequence
under suitable control conditions. However, the sequence  excluded the canonical choice
excluded the canonical choice  . This was a motivation for Zhang-Guo [13] to improve the results in the same space. Observe that the results of Osilike-Udomene [11] and Zhang-Guo [13] hold under the assumption that
. This was a motivation for Zhang-Guo [13] to improve the results in the same space. Observe that the results of Osilike-Udomene [11] and Zhang-Guo [13] hold under the assumption that

for some  and
and  is a constant depending on the geometry of the space.
is a constant depending on the geometry of the space.
Let  be a uniformly smooth real Banach space. Then there exists a nondecreasing continuous function
be a uniformly smooth real Banach space. Then there exists a nondecreasing continuous function  with
with  and
and  for
for  such that, for all
such that, for all  , the following inequality holds:
, the following inequality holds:

Recently, Chidume-Shahzad [17] extended the results of Osilike-Udomene [11] and Zhang-Guo [13] by using Reich's inequality (1.10) to the much more general real Banach spaces which are uniformly smooth and uniformly convex. Under the assumption that

for some  , they proved the following theorem.
, they proved the following theorem.
Theorem 1.6 (see [17]).
Let  be a uniformly smooth real Banach space which is also uniformly convex and
be a uniformly smooth real Banach space which is also uniformly convex and  a nonempty closed convex subset of
a nonempty closed convex subset of  . Let
. Let  be a
be a  -strict pseudocontraction for some
-strict pseudocontraction for some  with
with  . For a fixed
. For a fixed  , define a sequence
, define a sequence  by
by

where  is a real sequence in
is a real sequence in  satisfying the following conditions:
satisfying the following conditions:
(i) ;
;
(ii) .
.
Then,  converges weakly to a fixed point of
converges weakly to a fixed point of  .
.
However, we would like to point out that the results of Chidume-Shahzad [17] do not hold in real Hilbert spaces. Indeed, we know from Chidume [14] that

If  is a real Hilbert space, then we have
is a real Hilbert space, then we have

On the other hand, by assumption (1.11), we see that

which is a contradiction.
It is known that one can extend his result from a single strict pseudocontraction to a finite family of strict pseudocontractions by replacing the convex combination of these mappings in the iteration under suitable conditions. The construction of fixed points for pseudocontractions via the iterative process has been extensively investigated by many authors; see also [18–22] and the references therein.
Our motivation in this paper is the following:
(1)to modify the normal Mann iteration process for finding common fixed points of an infinitely countable family of strict pseudocontractions,
(2)to improve and extend the results of Chidume-Shahzad [17] from a real uniformly smooth and uniformly convex Banach space to a real uniformly convex Banach space which has the Fréchet differentiable norm.
Motivated and inspired by Marino-Xu [7], Osilike-Udomene [11], Zhou [8], Zhang-Guo [13], and Chidume-Shahzad [17], we consider the following Mann-type iteration:  and
and

where  is a real sequence in
is a real sequence in  and
and  is a countable family of strict pseudocontractions on a closed and convex subset
is a countable family of strict pseudocontractions on a closed and convex subset  of a real Banach space
of a real Banach space  .
.
In this paper, we prove the weak convergence of a Mann-type iteration process (1.16) in a uniformly convex Banach space which has the Fréchet differentiable norm for a countable family of strict pseudocontractions under some appropriate conditions. The results obtained in this paper improve and extend the results of Chidume-Shahzad [17], Marino-Xu [7], Osilike-Udomene [11], Zhou [8], and Zhang-Guo [13] in some aspects.
We will use the following notation:
(i) for weak convergence and
for weak convergence and  for strong convergence.
for strong convergence.
(ii) denotes the weak
denotes the weak  -limit set of
-limit set of  .
.
2. Preliminaries
A Banach space  is said to be strictly convex if
is said to be strictly convex if  for all
for all  with
with  and
and  . A Banach space
. A Banach space  is called uniformly convex if for each
is called uniformly convex if for each  there is a
there is a  such that, for
such that, for  with
with  , and
, and  holds. The modulus of convexity of
holds. The modulus of convexity of  is defined by
is defined by

for all  .
.  is uniformly convex if
is uniformly convex if  , and
, and  for all
for all  . It is known that every uniformly convex Banach space is strictly convex and reflexive. Let
. It is known that every uniformly convex Banach space is strictly convex and reflexive. Let  . Then the norm of
. Then the norm of  is said to be Gâteaux differentiable if
is said to be Gâteaux differentiable if

exists for each  . In this case
. In this case  is called smooth. The norm of
is called smooth. The norm of  is said to be Fréchet differentiable or
is said to be Fréchet differentiable or  is Fréchet smooth if, for each
is Fréchet smooth if, for each  , the limit is attained uniformly for
, the limit is attained uniformly for  . In other words, there exists a function
. In other words, there exists a function  with
with  as
as  such that
such that

for all  . In this case the norm is Gâteaux differentiable and
. In this case the norm is Gâteaux differentiable and

for all  . On the other hand,
. On the other hand,

for all  , where
, where  is a function defined on
is a function defined on  such that
such that  . The norm of
. The norm of  is called uniformly Fréchet differentiable if the limit is attained uniformly for
is called uniformly Fréchet differentiable if the limit is attained uniformly for  .
.
Let  be the modulus of smoothness of
be the modulus of smoothness of  defined by
defined by

A Banach space  is said to be uniformly smooth if
is said to be uniformly smooth if  as
as  . Let
. Let  , then
, then  is said to be
is said to be  -uniformly smooth if there exists
-uniformly smooth if there exists  such that
such that  . It is easy to see that if
. It is easy to see that if  is
is  -uniformly smooth, then
-uniformly smooth, then  is uniformly smooth. It is well known that
is uniformly smooth. It is well known that  is uniformly smooth if and only if the norm of
is uniformly smooth if and only if the norm of  is uniformly Fréchet differentiable, and hence the norm of
is uniformly Fréchet differentiable, and hence the norm of  is Fréchet differentiable, and it is also known that if
is Fréchet differentiable, and it is also known that if  is Fréchet smooth, then
is Fréchet smooth, then  is smooth. Moreover, every uniformly smooth Banach space is reflexive. For more details, we refer the reader to [14, 23]. A Banach space
is smooth. Moreover, every uniformly smooth Banach space is reflexive. For more details, we refer the reader to [14, 23]. A Banach space  is said to satisfy Opial's condition [24] if
is said to satisfy Opial's condition [24] if  and
and  ; then
; then

In the sequel, we will need the following lemmas.
Lemma 2.1 (see [23]).
Let  be a Banach space and
be a Banach space and  the duality mapping. Then one has the following:
the duality mapping. Then one has the following:
(i) for all
for all  , where
, where  ;
;
(ii) for all
for all  , where
, where  .
.
Lemma 2.2 (see [25]).
Let  be a real uniformly convex Banach space,
be a real uniformly convex Banach space,  a nonempty, closed, and convex subset of
a nonempty, closed, and convex subset of  , and
, and  a continuous pseudocontractive mapping. Then,
a continuous pseudocontractive mapping. Then,  is demiclosed at zero, that is, for all sequence
is demiclosed at zero, that is, for all sequence  with
with  and
and  it follows that
it follows that  .
.
Lemma 2.3 (see [25]).
Let  be a real reflexive Banach space which satisfies Opial's condition,
be a real reflexive Banach space which satisfies Opial's condition,  a nonempty, closed and convex subset of
a nonempty, closed and convex subset of  and
and  a continuous pseudocontractive mapping. Then,
a continuous pseudocontractive mapping. Then,  is demiclosed at zero.
is demiclosed at zero.
Lemma 2.4 (see [26]).
Let  be a real uniformly convex Banach space with a Fréchet differentiable norm. Let
be a real uniformly convex Banach space with a Fréchet differentiable norm. Let  be a closed and convex subset of
be a closed and convex subset of  and
and  a family of
a family of  -Lipschitzian self-mappings on
-Lipschitzian self-mappings on  such that
such that  and
and  . For arbitrary
. For arbitrary , define
, define  for all
for all  . Then for every
. Then for every  ,
,  exists, in particular, for all
exists, in particular, for all  and
and  ,
,  .
.
Let  and
and  , be sequences of nonnegative real numbers satisfying the inequality
, be sequences of nonnegative real numbers satisfying the inequality

If  and
and  , then
, then  exists. If, in addition,
exists. If, in addition,  has a subsequence converging to 0, then
has a subsequence converging to 0, then  .
.
To deal with a family of mappings, the following conditions are introduced. Let  be a subset of a real Banach space
be a subset of a real Banach space  , and let
, and let  be a family of mappings of
be a family of mappings of  such that
such that  . Then
. Then  is said to satisfy the AKTT-condition [28] if for each bounded subset
is said to satisfy the AKTT-condition [28] if for each bounded subset  of
of  ,
,

Lemma 2.6 (see [28]).
Let  be a nonempty and closed subset of a Banach space
be a nonempty and closed subset of a Banach space  , and let
, and let  be a family of mappings of
be a family of mappings of  into itself which satisfies the AKTT-condition, then the mapping
into itself which satisfies the AKTT-condition, then the mapping  defined by
defined by

satisfies

for each bounded subset  of
of  .
.
So we have the following results proved by Boonchari-Saejung [29, 30].
Let  be a closed and convex subset of a smooth Banach space
be a closed and convex subset of a smooth Banach space  . Suppose that
. Suppose that  is a family of
is a family of  -strictly pseudocontractive mappings from
-strictly pseudocontractive mappings from  into
into  with
with  and
and  is a real sequence in
is a real sequence in  such that
such that  . Then the following conclusions hold:
. Then the following conclusions hold:
(1) is a
is a  -strictly pseudocontractive mapping;
-strictly pseudocontractive mapping;
(2) .
.
Lemma 2.8 (see [30]).
Let  be a closed and convex subset of a smooth Banach space
be a closed and convex subset of a smooth Banach space  . Suppose that
. Suppose that  is a countable family of
is a countable family of  -strictly pseudocontractive mappings of
-strictly pseudocontractive mappings of  into itself with
into itself with  . For each
. For each  , define
, define  by
by

where  is a family of nonnegative numbers satisfying
is a family of nonnegative numbers satisfying
(i) for all
for all  ;
;
(ii) for all
for all  ;
;
(iii) .
.
Then
(1)each  is a
is a  -strictly pseudocontractive mapping;
-strictly pseudocontractive mapping;
(2) satisfies AKTT-condition;
satisfies AKTT-condition;
(3)If  is defined by
is defined by

then  and
and  .
.
For convenience, we will write that  satisfies the AKTT-condition if
satisfies the AKTT-condition if  satisfies the AKTT-condition and
satisfies the AKTT-condition and  is defined by Lemma 2.6 with
is defined by Lemma 2.6 with  .
.
3. Main Results
Lemma 3.1.
Let  be a real Banach space, and let
be a real Banach space, and let  be a nonempty, closed, and convex subset of
be a nonempty, closed, and convex subset of  . Let
. Let  be a family of
be a family of  -strict pseudocontractions for some
-strict pseudocontractions for some  such that
such that  . Define a sequence
. Define a sequence  by
by  ,
,

where  satisfying
satisfying  and
and  . If
. If  satisfies the AKTT-condition, then
satisfies the AKTT-condition, then
(i) exists for all
exists for all  ;
;
(ii) .
.
Proof.
Let  , and put
, and put  . First, we observe that
. First, we observe that

Since  is a
is a  -strict pseudocontraction, there exists
-strict pseudocontraction, there exists  . By Lemma 2.1 we have
. By Lemma 2.1 we have

This implies that

Hence, by  , we have from Lemma 2.5 that
, we have from Lemma 2.5 that  exists; consequently,
exists; consequently,  is bounded. Moreover, by (3.3), we also have
is bounded. Moreover, by (3.3), we also have

where  . It follows that
. It follows that  . Since
. Since  is bounded,
is bounded,

Since  satisfies the AKTT-condition, it follows that
satisfies the AKTT-condition, it follows that  . This completes the proof of (i) and (ii).
. This completes the proof of (i) and (ii).
Lemma 3.2.
Let  be a real Banach space with the Fréchet differentiable norm. For
be a real Banach space with the Fréchet differentiable norm. For  , let
, let  be defined for
be defined for  by
by

Then,  , and
, and

for all  .
.
Proof.
Let  . Since
. Since  has the Fréchet differentiable norm, it follows that
has the Fréchet differentiable norm, it follows that

Then  , and hence
, and hence

which implies that

Suppose that  . Put
. Put  and
and  . By (3.11), we have
. By (3.11), we have

This completes the proof.
Remark 3.3.
In a real Hilbert space, we see that  for
for  .
.
In our more general setting, throughout this paper we will assume that

where  is a function appearing in (3.8).
is a function appearing in (3.8).
So we obtain the following results.
Lemma 3.4.
Let  be a real Banach space with the Fréchet differentiable norm, and let
be a real Banach space with the Fréchet differentiable norm, and let  be a nonempty, closed, and convex subset of
be a nonempty, closed, and convex subset of  . Let
. Let  be a family of
be a family of  -strict pseudocontractions for some
-strict pseudocontractions for some  such that
such that  . Define a sequence
. Define a sequence  by
by  ,
,

where  satisfying
satisfying  and
and  . If
. If  satisfies the AKTT-condition, then
satisfies the AKTT-condition, then  .
.
Proof.
Let  , and put
, and put  . Then by (3.8) and (3.13) we have
. Then by (3.8) and (3.13) we have

It follows that

Observe that

By (3.17), we have

Since  ,
,  , and
, and  , it follows from Lemma 2.5 that
, it follows from Lemma 2.5 that  exists. Hence, by Lemma 3.1(ii), we can conclude that
exists. Hence, by Lemma 3.1(ii), we can conclude that  . Since
. Since

it follows from Lemma 2.6 that  . This completes the proof.
. This completes the proof.
Now, we prove our main result.
Theorem 3.5.
Let  be a real uniformly convex Banach space with the Fréchet differentiable norm, and let
be a real uniformly convex Banach space with the Fréchet differentiable norm, and let  be a nonempty, closed, and convex subset of
be a nonempty, closed, and convex subset of  . Let
. Let  be a family of
be a family of  -strict pseudocontractions for some
-strict pseudocontractions for some  such that
such that  . Define a sequence
. Define a sequence  by
by  ,
,

where  satisfying
satisfying  and
and  . If
. If  satisfies the AKTT-condition, then
satisfies the AKTT-condition, then  converges weakly to a common fixed point of
converges weakly to a common fixed point of  .
.
Proof.
Let  , and define
, and define  by
by

Then  . By (3.8), we have for bounded
. By (3.8), we have for bounded  that
that

This implies that  is nonexpansive. By Lemma 3.1(i), we know that
is nonexpansive. By Lemma 3.1(i), we know that  is bounded. By Lemma 3.4, we also know that
is bounded. By Lemma 3.4, we also know that  . Applying Lemma 2.2, we also have
. Applying Lemma 2.2, we also have  .
.
Finally, we will show that  is a singleton. Suppose that
is a singleton. Suppose that  . Hence
. Hence  . By Lemma 2.4,
. By Lemma 2.4,  exists. Suppose that
exists. Suppose that  and
and  are subsequences of
are subsequences of  such that
such that  and
and  . Then
. Then

Hence  ; consequently,
; consequently,  as
as  . This completes the proof.
. This completes the proof.
As a direct consequence of Theorem 3.5, Lemmas 2.7 and 2.8 we also obtain the following results.
Theorem 3.6.
Let  be a real uniformly convex Banach space with the Fréchet differentiable norm, and let
be a real uniformly convex Banach space with the Fréchet differentiable norm, and let  be a nonempty, closed, and convex subset of
be a nonempty, closed, and convex subset of  . Let
. Let  be a sequence of
be a sequence of  -strict pseudocontractions of
-strict pseudocontractions of  into itself such that
into itself such that  and
and  . Define a sequence
. Define a sequence  by
by  ,
,

where  satisfying
satisfying  and
and  and
and  satisfies conditions (i)–(iii) of Lemma 2.8. Then,
satisfies conditions (i)–(iii) of Lemma 2.8. Then,  converges weakly to a common fixed point of
converges weakly to a common fixed point of  .
.
Remark 3.7.
-
(i)
Theorems 3.5 and 3.6 extend and improve Theorems
 and
and 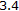 of Chidume-Shahzad [17] in the following senses:
of Chidume-Shahzad [17] in the following senses:
(i)from real uniformly smooth and uniformly convex Banach spaces to real uniformly convex Banach spaces with Fréchet differentiable norms;
(ii)from finite strict pseudocontractions to infinite strict pseudocontractions.
Using Opial's condition, we also obtain the following results in a real reflexive Banach space.
Theorem 3.8.
Let  be a real Fréchet smooth and reflexive Banach space which satisfies Opial's condition, and let
be a real Fréchet smooth and reflexive Banach space which satisfies Opial's condition, and let  be a nonempty, closed, and convex subset of
be a nonempty, closed, and convex subset of  . Let
. Let  be a family of
be a family of  -strict pseudocontractions for some
-strict pseudocontractions for some  such that
such that  . Define a sequence
. Define a sequence  by
by  ,
,

where  satisfying
satisfying  and
and  . If
. If  satisfies the AKTT-condition, then
satisfies the AKTT-condition, then  converges weakly to a common fixed point of
converges weakly to a common fixed point of  .
.
Proof.
Let  . By Lemma 3.1(i), we know that
. By Lemma 3.1(i), we know that  exists. Since
exists. Since  has the Fréchet differentiable norm, by Lemma 3.4, we know that
has the Fréchet differentiable norm, by Lemma 3.4, we know that  . It follows from Lemma 2.3 that
. It follows from Lemma 2.3 that  . Finally, we show that
. Finally, we show that  is a singleton. Let
is a singleton. Let  , and let
, and let  and
and  be subsequences of
be subsequences of  chosen so that
chosen so that  and
and  . If
. If  , then Opial's condition of
, then Opial's condition of  implies that
implies that

This is a contradiction, and thus the proof is complete.
Theorem 3.9.
Let  be a real Fréchet smooth and reflexive Banach space which satisfies Opial's condition, and let
be a real Fréchet smooth and reflexive Banach space which satisfies Opial's condition, and let  be a nonempty, closed, and convex subset of
be a nonempty, closed, and convex subset of  . Let
. Let  be a sequence of
be a sequence of  -strict pseudocontractions of
-strict pseudocontractions of  into itself such that
into itself such that  and
and  . Define a sequence
. Define a sequence  by
by  ,
,

where  satisfying
satisfying  and
and  and
and  satisfies conditions (i)–(iii) of Lemma 2.8. Then,
satisfies conditions (i)–(iii) of Lemma 2.8. Then,  converges weakly to a common fixed point of
converges weakly to a common fixed point of  .
.
References
Browder FE: Nonlinear operators and nonlinear equations of evolution in Banach spaces. In Nonlinear Functional Analysis (Proc. Sympos. Pure Math., Vol. XVIII, Part 2, Chicago, Ill., 1968). American Mathematical Society, Providence, RI, USA; 1976:1–308.
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
Chen R, Song Y, Zhou H: Convergence theorems for implicit iteration process for a finite family of continuous pseudocontractive mappings. Journal of Mathematical Analysis and Applications 2006,314(2):701–709. 10.1016/j.jmaa.2005.04.018
Chidume CE, Mutangadura SA: An example of the Mann iteration method for Lipschitz pseudocontractions. Proceedings of the American Mathematical Society 2001,129(8):2359–2363. 10.1090/S0002-9939-01-06009-9
Mann WR: Mean value methods in iteration. Proceedings of the American Mathematical Society 1953, 4: 506–510. 10.1090/S0002-9939-1953-0054846-3
Reich S: Weak convergence theorems for nonexpansive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 1979,67(2):274–276. 10.1016/0022-247X(79)90024-6
Marino G, Xu H-K: Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,329(1):336–346. 10.1016/j.jmaa.2006.06.055
Zhou H: Convergence theorems of fixed points for Lipschitz pseudo-contractions in Hilbert spaces. Journal of Mathematical Analysis and Applications 2008,343(1):546–556. 10.1016/j.jmaa.2008.01.045
Zhou H: Convergence theorems for -strict pseudo-contractions in 2-uniformly smooth Banach spaces. Nonlinear Analysis 2008,69(9):3160–3173. 10.1016/j.na.2007.09.009
Zhang H, Su Y: Convergence theorems for strict pseudo-contractions in -uniformly smooth Banach spaces. Nonlinear Analysis 2009,71(10):4572–4580. 10.1016/j.na.2009.03.033
Osilike MO, Udomene A: Demiclosedness principle and convergence theorems for strictly pseudocontractive mappings of Browder-Petryshyn type. Journal of Mathematical Analysis and Applications 2001,256(2):431–445. 10.1006/jmaa.2000.7257
Ishikawa S: Fixed points by a new iteration method. Proceedings of the American Mathematical Society 1974, 44: 147–150. 10.1090/S0002-9939-1974-0336469-5
Zhang Y, Guo Y: Weak convergence theorems of three iterative methods for strictly pseudocontractive mappings of Browder-Petryshyn type. Fixed Point Theory and Applications 2008, 2008:-13.
Chidume CE: Geometric Properties of Banach Spaces and Nonlinear Iterations, Lecture Notes Series. Springer, New York, NY, USA; 2009.
Reich S: Constructive techniques for accretive and monotone operators. In Applied Nonlinear Analysis. Academic Press, New York, NY, USA; 1979:335–345.
Reich S: An iterative procedure for constructing zeros of accretive sets in Banach spaces. Nonlinear Analysis 1978,2(1):85–92. 10.1016/0362-546X(78)90044-5
Chidume CE, Shahzad N: Weak convergence theorems for a finite family of strict pseudocontractions. Nonlinear Analysis 2010,72(3–4):1257–1265. 10.1016/j.na.2009.08.009
Ceng LC, Ansari QH, Yao JC: Strong and weak convergence theorems for asymptotically strict pseudocontractive mappings in intermediate sense. Journal of Nonlinear and Convex Analysis 2010, 11: 283–308.
Ceng LC, Shyu DS, Yao JC: Relaxed composite implicit iteration process for common fixed points of a finite family of strictly pseudocontractive mappings. Fixed Point Theory and Applications 2009, 2009:-16.
Ceng L-C, Petruşel A, Yao J-C: Strong convergence of modified implicit iterative algorithms with perturbed mappings for continuous pseudocontractive mappings. Applied Mathematics and Computation 2009,209(2):162–176. 10.1016/j.amc.2008.10.062
Ceng L-C, Al-Homidan S, Ansari QH, Yao J-C: An iterative scheme for equilibrium problems and fixed point problems of strict pseudo-contraction mappings. Journal of Computational and Applied Mathematics 2009,223(2):967–974. 10.1016/j.cam.2008.03.032
Peng J-W, Yao J-C: Ishikawa iterative algorithms for a generalized equilibrium problem and fixed point problems of a pseudo-contraction mapping. Journal of Global Optimization 2010,46(3):331–345. 10.1007/s10898-009-9428-9
Agarwal RP, O'Regan D, Sahu DR: Fixed Point Theory for Lipschitzian-Type Mappings with Applications, Topological Fixed Point Theory and Its Applications. Volume 6. Springer, New York, NY, USA; 2009:x+368.
Opial Z: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bulletin of the American Mathematical Society 1967, 73: 591–597. 10.1090/S0002-9904-1967-11761-0
Zhou H: Convergence theorems of common fixed points for a finite family of Lipschitz pseudocontractions in Banach spaces. Nonlinear Analysis 2008,68(10):2977–2983. 10.1016/j.na.2007.02.041
Tan K-K, Xu HK: Fixed point iteration processes for asymptotically nonexpansive mappings. Proceedings of the American Mathematical Society 1994,122(3):733–739. 10.1090/S0002-9939-1994-1203993-5
Tan K-K, Xu HK: Approximating fixed points of nonexpansive mappings by the Ishikawa iteration process. Journal of Mathematical Analysis and Applications 1993,178(2):301–308. 10.1006/jmaa.1993.1309
Aoyama K, Kimura Y, Takahashi W, Toyoda M: Approximation of common fixed points of a countable family of nonexpansive mappings in a Banach space. Nonlinear Analysis 2007,67(8):2350–2360. 10.1016/j.na.2006.08.032
Boonchari D, Saejung S: Weak and strong convergence theorems of an implicit iteration for a countable family of continuous pseudocontractive mappings. Journal of Computational and Applied Mathematics 2009,233(4):1108–1116. 10.1016/j.cam.2009.09.007
Boonchari D, Saejung S: Construction of common fixed points of a countable family of -demicontractive mappings in arbitrary Banach spaces. Applied Mathematics and Computation 2010,216(1):173–178. 10.1016/j.amc.2010.01.027
Acknowledgments
The authors would like to thank the referees for valuable suggestions. This research is supported by the Centre of Excellence in Mathematics, the Commission on Higher Education, and the Thailand Research Fund, Thailand. The first author is supported by the Royal Golden Jubilee Grant PHD/0261/2551 and by the Graduate School, Chiang Mai University, Thailand.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cholamjiak, P., Suantai, S. Weak Convergence Theorems for a Countable Family of Strict Pseudocontractions in Banach Spaces. Fixed Point Theory Appl 2010, 632137 (2010). https://doi.org/10.1155/2010/632137
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/632137
 and
and 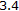 of Chidume-Shahzad [
of Chidume-Shahzad [