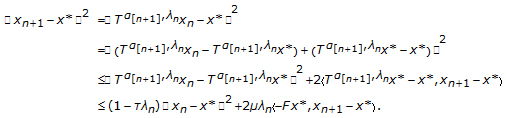- Research Article
- Open access
- Published:
Hybrid Steepest-Descent Methods for Solving Variational Inequalities Governed by Boundedly Lipschitzian and Strongly Monotone Operators
Fixed Point Theory and Applications volume 2010, Article number: 673932 (2010)
Abstract
Let  be a real Hilbert space and let
be a real Hilbert space and let  be a boundedly Lipschitzian and strongly monotone operator. We design three hybrid steepest descent algorithms for solving variational inequality
be a boundedly Lipschitzian and strongly monotone operator. We design three hybrid steepest descent algorithms for solving variational inequality  of finding a point
of finding a point  such that
such that  , for all
, for all  , where
, where  is the set of fixed points of a strict pseudocontraction, or the set of common fixed points of finite strict pseudocontractions. Strong convergence of the algorithms is proved.
is the set of fixed points of a strict pseudocontraction, or the set of common fixed points of finite strict pseudocontractions. Strong convergence of the algorithms is proved.
1. Introduction
Let  be a real Hilbert space with the inner product
be a real Hilbert space with the inner product  and the norm
and the norm  , let
, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and let
and let  be a nonlinear operator. We consider the problem of finding a point
be a nonlinear operator. We consider the problem of finding a point  such that
such that

This is known as the variational inequality problem (i.e.,  initially introduced and studied by Stampacchia [1] in 1964. In the recent years, variational inequality problems have been extended to study a large variety of problems arising in structural analysis, economics, optimization, operations research, and engineering sciences; see [1–6] and the references therein.
initially introduced and studied by Stampacchia [1] in 1964. In the recent years, variational inequality problems have been extended to study a large variety of problems arising in structural analysis, economics, optimization, operations research, and engineering sciences; see [1–6] and the references therein.
Yamada [7] proposed hybrid methods to solve  , where
, where  is composed of fixed points of a nonexpansive mapping; that is,
is composed of fixed points of a nonexpansive mapping; that is,  is of the form
is of the form

where  is a nonexpansive mapping (i.e.,
is a nonexpansive mapping (i.e.,  for all
for all  ),
),  is Lipschitzian and strongly monotone.
is Lipschitzian and strongly monotone.
He and Xu [8] proved that  has a unique solution and iterative algorithms can be devised to approximate this solution if
has a unique solution and iterative algorithms can be devised to approximate this solution if  is a boundedly Lipschitzian and strongly monotone operator and
is a boundedly Lipschitzian and strongly monotone operator and  is a closed convex subset of
is a closed convex subset of  . In the case where
. In the case where  is the set of fixed points of a nonexpansive mapping, they invented a hybrid iterative algorithm to approximate the unique solution of
is the set of fixed points of a nonexpansive mapping, they invented a hybrid iterative algorithm to approximate the unique solution of  and this extended the Yamada's results.
and this extended the Yamada's results.
The main purpose of this paper is to continue our research in [8]. We assume that  is a boundedly Lipschitzian and strongly monotone operator as in [8], but
is a boundedly Lipschitzian and strongly monotone operator as in [8], but  is the set of fixed points of a strict pseudo-contraction
is the set of fixed points of a strict pseudo-contraction  , or the set of common fixed points of finite strict pseudo-contractions
, or the set of common fixed points of finite strict pseudo-contractions  . For the two cases of
. For the two cases of  , we will design the hybrid iterative algorithms for solving
, we will design the hybrid iterative algorithms for solving  and prove their strong convergence, respectively. Relative definitions are stated as below.
and prove their strong convergence, respectively. Relative definitions are stated as below.
Let  be a nonempty closed and convex subset of a real Hilbert space
be a nonempty closed and convex subset of a real Hilbert space  ,
,  and
and  , then
, then
(1) is called Lipschitzian on
is called Lipschitzian on  , if there there exists a positive constant
, if there there exists a positive constant  such that
such that

(2) is called boundedly Lipschitzian on
is called boundedly Lipschitzian on  , if for each nonempty bounded subset
, if for each nonempty bounded subset  of
of  , there exists a positive constant
, there exists a positive constant  depending only on the set
depending only on the set  such that
such that

(3) is said to be
is said to be  -strongly monotone on
-strongly monotone on  , if there exists a positive constant
, if there exists a positive constant  such that
such that

(4) is said to be a
is said to be a  -strict pseudo-contraction if there exists a constant
-strict pseudo-contraction if there exists a constant  such that
such that

Obviously, the nonexpansive mapping class is a proper subclass of the strict pseudo-contraction class and the Lipschitzian operator class is a proper subclass of the boundedly Lipschitzian operator class, respectively.
We will use the following notations:
(i) for weak convergence and
for weak convergence and  for strong convergence,
for strong convergence,
(ii) denotes the weak
denotes the weak  -limit set of
-limit set of 
(iii) denotes a closed ball with center
denotes a closed ball with center  and radius
and radius  .
.
2. Preliminaries
We need some facts and tools which are listed as lemmas below.
Lemma 2.1.
Let  be a real Hilbert space. The following expressions hold:
be a real Hilbert space. The following expressions hold:
(i)
(ii)
Lemma 2.2 (see [9]).
Assume that  is a sequence of nonnegtive real numbers satisfying the property
is a sequence of nonnegtive real numbers satisfying the property

If  and
and  satisfy the following conditions:
satisfy the following conditions:
(i)
(ii)
(iii)
then 
Lemma 2.3 (see [10]).
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  and
and  is a nonexpansive mapping. If a one has sequence
is a nonexpansive mapping. If a one has sequence  in
in  such that
such that  and
and  then
then 
Lemma 2.4 (see [11]).
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  , if
, if is a
is a  -strict pseudo-contraction, then the mapping
-strict pseudo-contraction, then the mapping  is demiclosed at 0. That is, if
is demiclosed at 0. That is, if  is a sequence in
is a sequence in  such that
such that  and
and  then
then 
Lemma 2.5 (see [8]).
Assume that  is a nonempty closed convex subset of a real Hilbert space
is a nonempty closed convex subset of a real Hilbert space  ,
,  if
if  is boundedly Lipschitzian and
is boundedly Lipschitzian and  -strongly monotone, then variational inequality (1.1) has a unique solution.
-strongly monotone, then variational inequality (1.1) has a unique solution.
Lemma 2.6.
Assume that  is a
is a  -strict pseudo-contraction, and the constant
-strict pseudo-contraction, and the constant  satisfies
satisfies  Let
Let

then  is nonexpansive and
is nonexpansive and 
Proof.
Using Lemma 2.1(i) and the conception of  -strict pseudo-contraction, we get
-strict pseudo-contraction, we get

so  is nonexpansive.
is nonexpansive.  is obvious.
is obvious.
Lemma 2.7.
Assume that  is a real Hilbert space,
is a real Hilbert space,  is a
is a  -strict pseudo-contraction such that
-strict pseudo-contraction such that  and
and is a boundedly Lipschitzian and
is a boundedly Lipschitzian and  -strongly monotone operator. Take
-strongly monotone operator. Take  arbitrarily and set
arbitrarily and set  . Denote by
. Denote by  the Lipschitz constant of
the Lipschitz constant of  on
on  and let
and let

where the constants  and
and  are such that
are such that  and
and  , respectively, and
, respectively, and  is defined as in Lemma 2.6 above. Then
is defined as in Lemma 2.6 above. Then  restricted to
restricted to  is a contraction.
is a contraction.
Proof.
If  , that is,
, that is,  , by Lemma 2.6, we have
, by Lemma 2.6, we have

It suggests that  . Since
. Since  is Lipschitzian and
is Lipschitzian and  -strongly monotone on
-strongly monotone on  , using Lemma 2.6, we obtain
, using Lemma 2.6, we obtain

Therefore,  restricted to that
restricted to that  is a contraction with coefficient
is a contraction with coefficient  , where
, where 
Lemma 2.8 (see [11]).
Assume  is a closed convex subset of a Hilbert space
is a closed convex subset of a Hilbert space  .
.
(i)Given an integer  , assume that for each
, assume that for each  ,
,  is a
is a  -strict pseudo-contraction for some
-strict pseudo-contraction for some  . Assume
. Assume  is a positive sequence such that
is a positive sequence such that  . Then
. Then  is a
is a  -strict pseudo-contraction, with
-strict pseudo-contraction, with 
-
(ii)
Let
 ,
, 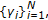 and
and  be given as in (i) above. Suppose that
be given as in (i) above. Suppose that 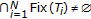 , then
, then

Lemma 2.9.
Assume that  is a
is a  -strict pseudo-contraction for some
-strict pseudo-contraction for some  let
let if
if  , then
, then

Proof.
We prove it by induction. For  , set
, set  ,
,  . Obviously
. Obviously

Now we prove

 , if
, if  , then
, then  the conclusion holds. In fact, we can claim that
the conclusion holds. In fact, we can claim that  . From Lemma 2.6, we know that
. From Lemma 2.6, we know that  is nonexpansive and
is nonexpansive and  Take
Take  , then
, then

Since  , we get
, we get

Namely,  that is,
that is,

Suppose that the conclusion holds for  , we prove that
, we prove that

It suffices to verify

 ,
,  . Using Lemma 2.6 again, take
. Using Lemma 2.6 again, take  ,
,

Since  , we have
, we have

this implies that

Namely,

From (2.19) and inductive assumption, we get

therefore

Substituting it into (2.19), we obtain  Thus we assert that
Thus we assert that

3. Further Extension of Hybrid Iterative Algorithm
Yamada got the following result.
Theorem 3.1 (see [7]).
Assume that  is a real Hilbert space,
is a real Hilbert space,  is nonexpansive such that
is nonexpansive such that  and
and  is
is  -strongly monotone and
-strongly monotone and  -Lipschitzian. Fix a constant
-Lipschitzian. Fix a constant  . Assume also that the sequence
. Assume also that the sequence  satisfies the following conditions:
satisfies the following conditions:
(i) ;
;
(ii)
(iii) , or
, or  .
.
Take  arbitrarily and define
arbitrarily and define  by
by

then  converges strongly to the unique solution of
converges strongly to the unique solution of  .
.
He and Xu [8] proved that  has a unique solution if
has a unique solution if  is a boundedly Lipschitzian and strongly monotone operator and
is a boundedly Lipschitzian and strongly monotone operator and  is a closed convex subset of
is a closed convex subset of  . Using this result, they were able to relax the global Lipschitz condition on
. Using this result, they were able to relax the global Lipschitz condition on  in Theorem 3.1 to the weaker bounded Lipschitz condition and invented a hybrid iterative algorithm to approximate the unique solution of
in Theorem 3.1 to the weaker bounded Lipschitz condition and invented a hybrid iterative algorithm to approximate the unique solution of  . Their result extended the Yamada's above theorem.
. Their result extended the Yamada's above theorem.
In this section, we mainly focus on further extension of our hybrid algorithm in [8]. Consider  , where
, where  is composed of fixed points of a
is composed of fixed points of a  -strict pseudo-contraction
-strict pseudo-contraction  such that
such that  and
and  is still
is still  -strongly monotone and boundedly Lipschitzian. Fix a point
-strongly monotone and boundedly Lipschitzian. Fix a point  arbitrarily, set
arbitrarily, set  . Denote by
. Denote by  the Lipschitz constant of
the Lipschitz constant of  on
on  . Fix the constant
. Fix the constant  satisfying
satisfying  . Assume also that the sequences
. Assume also that the sequences  and
and  satisfy
satisfy  for a constant
for a constant  and
and  , respectively. Let
, respectively. Let  and
and  , define
, define  by the scheme:
by the scheme:

We have the following result.
Theorem 3.2.
If the sequences  and
and  satisfy the following conditions:
satisfy the following conditions:
(i) ;
;
(ii)
(iii) ,
,  , or
, or  ,
, 
then  generated by (3.2) converges strongly to the unique solution
generated by (3.2) converges strongly to the unique solution  of
of .
.
Proof.
We prove that  for all
for all  by induction. It is trivial that
by induction. It is trivial that  . Suppose we have proved
. Suppose we have proved  , that is,
, that is,

Using Lemma 2.7, We then derive from (3.2) and (3.3) that

However, since  and
and  we get
we get

This together with (3.4) implies that

It proves that  . Therefore,
. Therefore,  for all
for all  . Thus
. Thus  is bounded. It is not difficult to verify that the sequences
is bounded. It is not difficult to verify that the sequences  and
and  are all bounded.
are all bounded.
By (3.2) and Lemma 2.7, we have

where  . By Lemma 2.2 and conditions (i)–(iii), we conclude that
. By Lemma 2.2 and conditions (i)–(iii), we conclude that

Since  , it is straitforward from (3.2) that
, it is straitforward from (3.2) that

On the other hand

By the condition  and (3.8)–(3.10), we obtain
and (3.8)–(3.10), we obtain

By Lemma 2.4 and (3.11), we obtain

Lemma 2.5 asserts that  has a unique solution
has a unique solution  . Now we prove that
. Now we prove that  . By Lemma 2.1(ii), (3.2), and Lemma 2.7, we have
. By Lemma 2.1(ii), (3.2), and Lemma 2.7, we have

Let us show that

In fact, there exists a subsequence  such that
such that

Without loss of generality, we may further assume that  . Since
. Since  is the unique solution of
is the unique solution of  , we obtain
, we obtain

Finally conditions (i)–(iii) and (3.14) allow us to apply Lemma 2.2 to the relation (3.13) to conclude that 
4. Parallel Algorithm and Cyclic Algorithm
In this section, we discuss the parallel algorithm and the cyclic algorithm, respectively, for solving the variational inequality over the set of the common fixed points of finite strict pseudo-contractions.
Let  be a real Hilbert space and
be a real Hilbert space and  a
a  -strongly monotone and boundedly Lipschitzian operator. Let
-strongly monotone and boundedly Lipschitzian operator. Let  be a positive integer and
be a positive integer and  a
a  -strict pseudo-contraction for some
-strict pseudo-contraction for some  such that
such that  We consider the problem of finding
We consider the problem of finding  such that
such that

Since  is a nonempty closed convex subset of
is a nonempty closed convex subset of  ,
,  (4.1) has a unique solution. Throughout this section,
(4.1) has a unique solution. Throughout this section,  is an arbitrary fixed point,
is an arbitrary fixed point,  ,
,  is the Lipschitz constant of
is the Lipschitz constant of  on
on  , the fixed constant
, the fixed constant  satisfies
satisfies  , and the sequence
, and the sequence  belongs to
belongs to  .
.
Firstly we consider the parallel algorithm. Take a positive sequence  such that
such that  and let
and let

By using Lemma 2.8, we assert that  is a
is a  -strict pseudo-contraction with
-strict pseudo-contraction with  and
and  holds. Thus VI(4.1) is equivalent to VI
holds. Thus VI(4.1) is equivalent to VI and we can use scheme (3.2) to solve VI(4.1). In fact, taking
and we can use scheme (3.2) to solve VI(4.1). In fact, taking  in the scheme (3.2), we get the so-called parallel algorithm
in the scheme (3.2), we get the so-called parallel algorithm

Using Lemma 2.8 and Thorem 3.2, the following conclusion can be deduced directly.
Theorem 4.1.
Suppose that  and
and  satisfy the same conditions as in Theorem 3.2. Then the sequence
satisfy the same conditions as in Theorem 3.2. Then the sequence  generated by the parallel algorithm (4.3) converges strongly to the unique solution
generated by the parallel algorithm (4.3) converges strongly to the unique solution  of
of  (4.1).
(4.1).
For each  let
let

where the constant  such that
such that  . Then we turn to defining the cyclic algorithm as follows:
. Then we turn to defining the cyclic algorithm as follows:

Indeed, the algorithm above can be rewritten as

where 
 , namely,
, namely,  is one of
is one of  circularly. For convenience, we denote (4.6) as
circularly. For convenience, we denote (4.6) as

We get the following result
Theorem 4.2.
If  satisfies the following conditions:
satisfies the following conditions:
(i) ;
;
(ii) ;
;
(iii) , or
, or 
then the sequence  generated by (4.6) converges strongly to the unique solution
generated by (4.6) converges strongly to the unique solution  of
of  .
.
Proof.
We break the proof process into six steps.
-
(1)
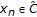 . We prove it by induction. Definitely
. We prove it by induction. Definitely 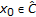 . Suppose
. Suppose 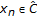 , that is,
, that is, 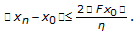 (4.8)
(4.8)
We have from  , (4.8), and Lemma 2.7 that
, (4.8), and Lemma 2.7 that

where  Observing
Observing  , we get
, we get

This together with (4.9) implies that

It suggests that  . Therefore,
. Therefore,  for all
for all  . We can also prove that the sequences
. We can also prove that the sequences  ,
,  ,
, are all bounded.
are all bounded.
-
(2)
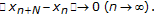 By (4.6) and Lemma 2.7, we have
By (4.6) and Lemma 2.7, we have 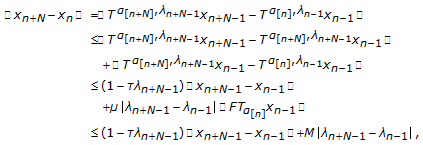 (4.12)
(4.12)
where  Since
Since  satisfies (i)–(iii), using Lemma 2.2, we get
satisfies (i)–(iii), using Lemma 2.2, we get

-
(3)
 By (4.3) and
By (4.3) and 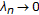 , we have
, we have 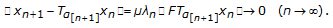 (4.14)
(4.14)
Recursively,

By Lemma 2.6,  is nonexpansive, we obtain
is nonexpansive, we obtain

Adding all the expressions above, we get

Using this together with the conclusion of step (2), we obtain

-
(4)
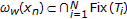 . Assume that
. Assume that 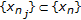 such that
such that  , we prove
, we prove 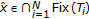 . By the conclusion of step (3), we get
. By the conclusion of step (3), we get 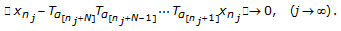 (4.19)
(4.19)
Observe that, for each  is some permutation of the mappings
is some permutation of the mappings  , since
, since  are finite, all the full permutation are
are finite, all the full permutation are  , there must be some permutation that appears infinite times. Without loss of generality, suppose that this permutation is
, there must be some permutation that appears infinite times. Without loss of generality, suppose that this permutation is  , we can take a subsequence
, we can take a subsequence  such that
such that

It is easy to prove that  is nonexpansive. By Lemma 2.3, we get
is nonexpansive. By Lemma 2.3, we get

Using Lemmas 2.6 and 2.9, we obtain

-
(5)
 In fact, there exists a subsequence
In fact, there exists a subsequence  such that
such that 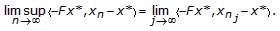 (4.23)
(4.23)
Without loss of generality, we may further assume that  Since
Since  is the solution of
is the solution of  , we obtain
, we obtain

-
(6)
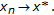 By (4.6), Lemmas 2.1(ii), and 2.7, we obtain
By (4.6), Lemmas 2.1(ii), and 2.7, we obtain 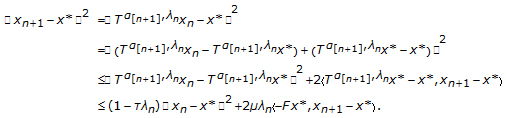 (4.25)
(4.25)
From the conclusion of step (5) and Lemma 2.2, we get

References
Stampacchia G: Formes bilinéaires coercitives sur les ensembles convexes. Comptes Rendus de l'Académie des Sciences 1964, 258: 4413–4416.
Cottle RW, Giannessi F, Lions JL: Variational Inequalities and Complementarity Problems: Theory and Applications. John Wiley & Sons, New York, NY, USA; 1980.
Fukushima M: Equivalent differentiable optimization problems and descent methods for asymmetric variational inequality problems. Mathematical Programming 1992,53(1):99–110. 10.1007/BF01585696
Geobel K, Reich S: Uniform Convexity, Nonexpansive Mappings, and Hyperbolic Geometry. Dekker, New York, NY, USA; 1984.
Glowinski R, Lions J-L, Trémolières R: Numerical Analysis of Variational Inequalities, Studies in Mathematics and Its Applications. Volume 8. North-Holland, Amsterdam, The Netherlands; 1981:xxix+776.
He BS: A class of implicit methods for monotone variational inequalities. In Reports of the Institute of Mathematics. Nanjing University, China; 1995.
Yamada I: The hybrid steepest descent method for the variational inequality problem over the intersection of fixed point sets of nonexpansive mappings. In Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications, Studies in Computational Mathematics. Volume 8. Edited by: Butnariu D, Censor Y, Reich S. North-Holland, Amsterdam, The Netherlands; 2001:473–504.
He SN, Xu HK: Variational inequalities governed by boundedly Lipschitzian and strongly monotone operators. Fixed Point Theory 2009,10(2):245–258.
Xu HK: Iterative algorithms for nonlinear operators. Journal of the London Mathematical Society 2002,66(1):240–256. 10.1112/S0024610702003332
Geobel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Acedo GL, Xu H-K: Iterative methods for strict pseudo-contractions in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 2007,67(7):2258–2271. 10.1016/j.na.2006.08.036
Acknowledgment
This research is supported by the Fundamental Research Funds for the Central Universities (GRANT:ZXH2009D021).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
He, S., Liang, XL. Hybrid Steepest-Descent Methods for Solving Variational Inequalities Governed by Boundedly Lipschitzian and Strongly Monotone Operators. Fixed Point Theory Appl 2010, 673932 (2010). https://doi.org/10.1155/2010/673932
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/673932
 ,
, 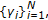 and
and  be given as in (i) above. Suppose that
be given as in (i) above. Suppose that 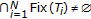 , then
, then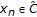 . We prove it by induction. Definitely
. We prove it by induction. Definitely 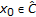 . Suppose
. Suppose 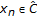 , that is,
, that is, 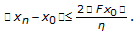
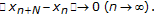 By (4.6) and Lemma 2.7, we have
By (4.6) and Lemma 2.7, we have 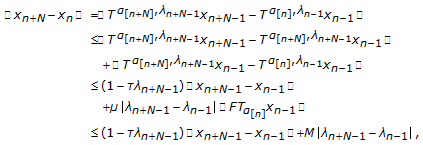
 By (4.3) and
By (4.3) and 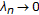 , we have
, we have 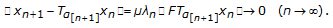
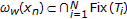 . Assume that
. Assume that 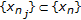 such that
such that  , we prove
, we prove 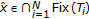 . By the conclusion of step (3), we get
. By the conclusion of step (3), we get 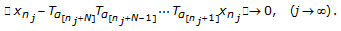
 In fact, there exists a subsequence
In fact, there exists a subsequence  such that
such that 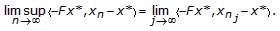
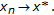 By (4.6), Lemmas 2.1(ii), and 2.7, we obtain
By (4.6), Lemmas 2.1(ii), and 2.7, we obtain