- Research Article
- Open access
- Published:
Common Fixed Point of Multivalued Generalized 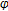 -Weak Contractive Mappings
-Weak Contractive Mappings
Fixed Point Theory and Applications volume 2010, Article number: 708984 (2010)
Abstract
Fixed point and coincidence results are presented for multivalued generalized  -weak contractive mappings on complete metric spaces, where
-weak contractive mappings on complete metric spaces, where  is a lower semicontinuous function with
is a lower semicontinuous function with  and
and  for all
for all  . Our results extend previous results by Zhang and Song (2009), as well as by Rhoades (2001), Nadler (1969), and Daffer and Kaneko (1995).
. Our results extend previous results by Zhang and Song (2009), as well as by Rhoades (2001), Nadler (1969), and Daffer and Kaneko (1995).
1. Introduction
Let  be a metric space. We denote the family of all nonempty closed and bounded subsets of
be a metric space. We denote the family of all nonempty closed and bounded subsets of  by
by  .
.
A mapping  is said to be
is said to be  -weak contractive if there exists a map
-weak contractive if there exists a map  with
with  and
and  for all
for all  such that
such that

for all  .
.
Also two mappings  are called generalized
are called generalized  -weak contractions if there exists a map
-weak contractions if there exists a map  with
with  and
and  for all
for all  such that
such that

for all  , where
, where

A mapping  is said to be a weak contraction if there exists
is said to be a weak contraction if there exists  such that
such that

for all  , where
, where  denotes the Hausdorff metric on
denotes the Hausdorff metric on  induced by
induced by  , that is,
, that is,

for all  , and where
, and where

A mapping  is said to be
is said to be  -weak contractive if there exists a map
-weak contractive if there exists a map  with
with  and
and  for all
for all  such that
such that

for all  .
.
The concepts of weak and  -weak contractive mappings were defined by Daffer and Kaneko [1] in 1995.
-weak contractive mappings were defined by Daffer and Kaneko [1] in 1995.
Many authors have studied fixed points for multivalued mappings. Among many others, see, for example, [1–4], and the references therein.
In the following theorem, Nadler [3] extended the Banach Contraction Principle to multivalued mappings.
Theorem 1.1.
Let  be a complete metric space. Suppose
be a complete metric space. Suppose  is a contraction mapping in the sense that for some
is a contraction mapping in the sense that for some  ,
,

for all  . Then there exists a point
. Then there exists a point  such that
such that  (i.e.,
(i.e.,  is a fixed point of
is a fixed point of  ).
).
Daffer and Kaneko [1] proved the existence of a fixed point for a multivalued weak contraction mapping of a complete metric space  into
into  .
.
Theorem 1.2.
Let  be a complete metric space and
be a complete metric space and  be such that
be such that

for some  and for all
and for all  (i.e., weak contraction). If
(i.e., weak contraction). If  is lower semicontinuous (l.s.c.), then there exists
is lower semicontinuous (l.s.c.), then there exists  such that
such that  .
.
In Section 3 we extend Nadler and Daffer-Kaneko's theorems to multivalued generalized weak contraction mappings (see Definition 2.1).
Rhoades [5, Theorem  ] proved the following fixed point theorem for
] proved the following fixed point theorem for  -weak contractive single valued mappings, giving another generalization of the Banach Contraction Principle.
-weak contractive single valued mappings, giving another generalization of the Banach Contraction Principle.
Theorem 1.3.
Let  be a complete metric space, and let
be a complete metric space, and let  be a mapping such that
be a mapping such that

for every  (i.e.,
(i.e.,  -weak contractive), where
-weak contractive), where  is a continuous and nondecreasing function with
is a continuous and nondecreasing function with  and
and  for all
for all  . Then
. Then  has a unique fixed point.
has a unique fixed point.
By choosing  ,
,  -weak contractions become mappings of Boyd and Wong type [6], and by defining
-weak contractions become mappings of Boyd and Wong type [6], and by defining  for
for  and
and  , then
, then  -weak contractions become mappings of Reich type [7].
-weak contractions become mappings of Reich type [7].
Recently Zhang and Song [8] proved the following theorem on the existence of a common fixed point for two single valued generalized  -weak contraction mappings.
-weak contraction mappings.
Theorem 1.4.
Let  be a complete metric space, and let
be a complete metric space, and let  be two mappings such that for all
be two mappings such that for all 

(i.e., generalized  -weak contractions), where
-weak contractions), where  is an l.s.c. function with
is an l.s.c. function with  and
and  for all
for all  . Then there exists a unique point
. Then there exists a unique point  such that
such that  .
.
In Section 4, we extend Theorem 1.3 by assuming  to be only l.s.c., and extend Theorem 1.4 to multivalued mappings.
to be only l.s.c., and extend Theorem 1.4 to multivalued mappings.
2. Preliminaries
In this paper,  denotes a complete metric space and
denotes a complete metric space and  denotes the Hausdorff metric on
denotes the Hausdorff metric on  .
.
Definition 2.1.
Two mappings  are called generalized weak contractions if there exists
are called generalized weak contractions if there exists  such that
such that

for all  .
.
Definition 2.2.
Two mappings  are called generalized
are called generalized  -weak contractive if there exists a map
-weak contractive if there exists a map  with
with  and
and  for all
for all  such that
such that

for all  .
.
In the proof of our main results, we will use the following well-known lemma, and refer to Nadler [3] or Assad and Kirk [9] for its proof.
Lemma 2.3.
If  and
and  , then for each
, then for each  , there exists
, there exists  such that
such that

3. Extension of Nadler and Daffer-Kaneko's Theorems
The following theorem extends Nadler and Daffer-Kaneko's Theorems to a coincidence theorem, without assuming  to be l.s.c.
to be l.s.c.
Theorem 3.1.
Let  be a complete metric space, and let
be a complete metric space, and let  be two multivalued mappings such that for all
be two multivalued mappings such that for all  ,
,

where  (i.e., multivalued generalized weak contractions). Then there exists a point
(i.e., multivalued generalized weak contractions). Then there exists a point  such that
such that  and
and  (i.e.,
(i.e.,  and
and  have a common fixed point). Moreover, if either
have a common fixed point). Moreover, if either  or
or  is single valued, then this common fixed point is unique.
is single valued, then this common fixed point is unique.
Proof.
Obviously  if and only if
if and only if  is a common fixed point of
is a common fixed point of  and
and  .
.
Let  be such that
be such that  . Let
. Let  and
and  . By Lemma 2.3, there exists
. By Lemma 2.3, there exists  such that
such that  . Again by using Lemma 2.3, there exists
. Again by using Lemma 2.3, there exists  such that
such that  . By induction and using Lemma 2.3, we can find in this way a sequence
. By induction and using Lemma 2.3, we can find in this way a sequence  in
in  such that
such that  and
and

and  and
and

It follows that

since if otherwise  , then
, then  and so
and so  . Hence
. Hence  and this is a contradiction.
and this is a contradiction.
Similarly,

From (3.4) and (3.5), we conclude that

for all  . Since
. Since  and (3.6) holds,
and (3.6) holds,  is a Cauchy sequence. Since
is a Cauchy sequence. Since  is complete, there exists
is complete, there exists  such that
such that 
We have

Letting  in the above inequality, we conclude that
in the above inequality, we conclude that  . So
. So  . Since
. Since  , we have
, we have  .
.
Similarly,  . Therefore,
. Therefore,  and
and  have a common fixed point.
have a common fixed point.
Furthermore, if  is single valued, then this common fixed point is unique. In fact, if
is single valued, then this common fixed point is unique. In fact, if  and
and  are two common fixed points for
are two common fixed points for  and
and  , then
, then

Since  ,
,  , and so
, and so  .
.
Remark 3.2.
The last part of the proof of Theorem 3.1 shows that if  are multivalued and
are multivalued and  is a common fixed point, and
is a common fixed point, and  or
or  is a singleton, then the common fixed point of
is a singleton, then the common fixed point of  and
and  is unique.
is unique.
By taking  in Theorem 3.1, we get the following corollary that extends the Daffer and Kaneko theorem (Theorem 1.2).
in Theorem 3.1, we get the following corollary that extends the Daffer and Kaneko theorem (Theorem 1.2).
Corollary 3.3.
Let  be a complete metric space and let
be a complete metric space and let  be such that
be such that

for some  and for all
and for all  (i.e., weak contraction). Then there exists
(i.e., weak contraction). Then there exists  such that
such that  .
.
Example 3.4.
Let  be endowed with the Euclidean metric. Let
be endowed with the Euclidean metric. Let  be defined by
be defined by  and
and  . Obviously,
. Obviously,

So  and
and  have a common fixed point (
have a common fixed point ( ), and since
), and since  is single valued, this fixed point is unique.
is single valued, this fixed point is unique.
4. Extension of Rhoades and Zhang-Song's Theorems
First we extend Zhang and Song's theorem (Theorem 1.4) to the case where one of the mappings is multivalued.
Theorem 4.1.
Let  be a complete metric space and let
be a complete metric space and let  and
and  be two mappings such that for all
be two mappings such that for all  ,
,

(i.e., generalized  -weak contractive) where
-weak contractive) where  is l.s.c. with
is l.s.c. with  and
and  for all
for all  . Then there exists a unique point
. Then there exists a unique point  such that
such that  .
.
Proof.
Unicity of the common fixed point follows from (4.1).
Obviously  if and only if
if and only if  is a common fixed point of
is a common fixed point of  and
and  .
.
Let  and
and  . Let
. Let  . By Lemma 2.3, there exists
. By Lemma 2.3, there exists  such that
such that

We let  . Inductively, we let
. Inductively, we let  , and by Lemma 2.3, we choose
, and by Lemma 2.3, we choose  such that
such that

We break the argument into four steps.
Step 1.

Proof.
Using (4.1) and (4.3),

where

So  . Hence by (4.4),
. Hence by (4.4),

Also

where

So  . Hence by (4.7),
. Hence by (4.7),

Therefore, by (4.6) and (4.9), we conclude that

for all  .
.
Therefore, the sequence  is monotone nonincreasing and bounded below. So there exists
is monotone nonincreasing and bounded below. So there exists  such that
such that

Since  is l.s.c.,
is l.s.c.,

By (4.4), we conclude that

and so  . Hence
. Hence  .
.
Step 2.
 is a bounded sequence.
is a bounded sequence.
Proof.
If  were unbounded, then by Step 1,
were unbounded, then by Step 1,  and
and  are unbounded. We choose the sequence
are unbounded. We choose the sequence  such that
such that  ,
,  is even and minimal in the sense that
is even and minimal in the sense that  , and
, and  , and similarly
, and similarly  is odd and minimal in the sense that
is odd and minimal in the sense that  , and
, and  is even and minimal in the sense that
is even and minimal in the sense that  and
and  , and
, and  is odd and minimal in the sense that
is odd and minimal in the sense that  and
and  .
.
Obviously  for every
for every  . By Step 1, there exists
. By Step 1, there exists  such that for all
such that for all  we have
we have  . So for every
. So for every  , we have
, we have  and
and

Hence  Also
Also

and this shows that 
So if  is odd, then
is odd, then

where

and this shows that  Since
Since  is l.s.c. and (4.16) holds, we have
is l.s.c. and (4.16) holds, we have  . So
. So  and this is a contradiction.
and this is a contradiction.
Step 3.
 is Cauchy.
is Cauchy.
Proof.
Let  . Since
. Since  is bounded,
is bounded,  for all
for all  . Obviously
. Obviously  is decreasing. So there exists
is decreasing. So there exists  such that
such that  . We need to show that
. We need to show that  .
.
For every  , there exists
, there exists  such that
such that  and
and

By (4.18), we conclude that

From Step 1 and (4.19), we have

So we may assume that for every  ,
,  is odd and
is odd and  is even. Hence
is even. Hence

where

This inequality shows that  Since
Since  is l.s.c. and (4.21) holds, we have
is l.s.c. and (4.21) holds, we have  . Hence
. Hence  and so
and so  . Therefore,
. Therefore,  is a Cauchy sequence.
is a Cauchy sequence.
Step 4.
 and
and  have a common fixed point.
have a common fixed point.
Proof.
Since  is complete and
is complete and  is Cauchy, there exists
is Cauchy, there exists  such that
such that  For every
For every

where

and this shows that 
Since  is l.s.c. and (4.23) holds, letting
is l.s.c. and (4.23) holds, letting  in (4.23) we get
in (4.23) we get

So  and hence
and hence  . Since
. Since  , then
, then  .Also
.Also

where

So from (4.26), we have

Thus  , and hence
, and hence  . Therefore,
. Therefore,  .
.
Remark 4.2.
In the proof of Theorem  in Zhang and Song [8], the boundedness of the sequence
in Zhang and Song [8], the boundedness of the sequence  is used, but not proved. Also, for the proof that
is used, but not proved. Also, for the proof that  is a Cauchy sequence, the monotonicity of
is a Cauchy sequence, the monotonicity of  is used, without being explicitly mentioned.
is used, without being explicitly mentioned.
In our proof of Theorem 4.1, which is different from [8, Theorem  ],
],  is not assumed to be nondecreasing.
is not assumed to be nondecreasing.
The following theorem extends Rhoades' theorem by assuming  to be only l.s.c..
to be only l.s.c..
Theorem 4.3.
Let  be a complete metric space, and let
be a complete metric space, and let  be a mapping such that
be a mapping such that

for every  (i.e.,
(i.e.,  -weak contractive), where
-weak contractive), where  is an l.s.c. function with
is an l.s.c. function with  and
and  for all
for all  . Then
. Then  has a unique fixed point.
has a unique fixed point.
Proof.
The proof is similar to the proof of Theorem 4.1, by taking  , and replacing
, and replacing  with
with  .
.
Remark 4.4.
With a similar proof as in Theorem 4.1, in Theorem 4.3 we can replace the inequality (4.29) by the following inequality (4.30) for two single valued mappings  .
.

5. Conclusion and Future Directions
We have extended Nadler and Daffer-Kaneko's theorems to a coincidence theorem without assuming the lower semicontinuity of the mapping  .
.
We have also extended Rhoades' theorem by assuming  to be only l.s.c., as well as Zhang and Song's theorem to the case where one of the mappings is multivalued. Future directions to be pursued in the context of this research include the investigation of the case where both mappings in Zhang and Song's theorem are multivalued.
to be only l.s.c., as well as Zhang and Song's theorem to the case where one of the mappings is multivalued. Future directions to be pursued in the context of this research include the investigation of the case where both mappings in Zhang and Song's theorem are multivalued.
References
Daffer PZ, Kaneko H: Fixed points of generalized contractive multi-valued mappings. Journal of Mathematical Analysis and Applications 1995,192(2):655–666. 10.1006/jmaa.1995.1194
Chifu C, Petrusel G: Existence and data dependence of fixed points and strict fixed points for contractive-type multivalued operators. Fixed Point Theory and Applications 2007, 2007:-8.
Nadler SB: Multi-valued contraction mappings. Pacific Journal of Mathematics 1969, 30: 475–488.
Shahzad N, Lone A: Fixed points of multimaps which are not necessarily nonexpansive. Fixed Point Theory and Applications 2005, (2):169–176.
Rhoades BE: Some theorems on weakly contractive maps. Nonlinear Analysis: Theory, Methods & Applications 2001,47(4):2683–2693. 10.1016/S0362-546X(01)00388-1
Boyd DW, Wong JSW: On nonlinear contractions. Proceedings of the American Mathematical Society 1969, 20: 458–464. 10.1090/S0002-9939-1969-0239559-9
Reich S: Some fixed point problems. Atti della Accademia Nazionale dei Lincei. Rendiconti. Classe di Scienze Fisiche, Matematiche e Naturali 1974,57(3–4):194–198.
Zhang Q, Song Y: Fixed point theory for generalized -weak contractions. Applied Mathematics Letters 2009,22(1):75–78. 10.1016/j.aml.2008.02.007
Assad NA, Kirk WA: Fixed point theorems for set-valued mappings of contractive type. Pacific Journal of Mathematics 1972, 43: 553–562.
Acknowledgment
This work is dedicated to Professor W. A. Kirk for his 70th birthday
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Djafari Rouhani, B., Moradi, S. Common Fixed Point of Multivalued Generalized 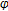 -Weak Contractive Mappings.
Fixed Point Theory Appl 2010, 708984 (2010). https://doi.org/10.1155/2010/708984
-Weak Contractive Mappings.
Fixed Point Theory Appl 2010, 708984 (2010). https://doi.org/10.1155/2010/708984
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/708984