- Research Article
- Open access
- Published:
Some Common Fixed Point Theorems in Menger PM Spaces
Fixed Point Theory and Applications volume 2010, Article number: 819269 (2010)
Abstract
Employing the common property (E.A), we prove some common fixed point theorems for weakly compatible mappings via an implicit relation in Menger PM spaces. Some results on similar lines satisfying quasicontraction condition as well as  -type contraction condition are also proved in Menger PM spaces. Our results substantially improve the corresponding theorems contained in (Branciari, (2002); Rhoades, (2003); Vijayaraju et al., (2005)) and also some others in Menger as well as metric spaces. Some related results are also derived besides furnishing illustrative examples.
-type contraction condition are also proved in Menger PM spaces. Our results substantially improve the corresponding theorems contained in (Branciari, (2002); Rhoades, (2003); Vijayaraju et al., (2005)) and also some others in Menger as well as metric spaces. Some related results are also derived besides furnishing illustrative examples.
1. Introduction and Preliminaries
Sometimes, it is found appropriate to assign the average of several measurements as a measure to ascertain the distance between two points. Inspired from this line of thinking, Menger [1, 2] introduced the notion of Probabilistic Metric spaces (in short PM spaces) as a generalization of metric spaces. In fact, he replaced the distance function  with a distribution function
with a distribution function  wherein for any number
wherein for any number  , the value
, the value  describes the probability that the distance between
describes the probability that the distance between  and
and  is less than
is less than  . In fact the study of such spaces received an impetus with the pioneering work of Schweizer and Sklar [3]. The theory of PM spaces is of paramount importance in Probabilistic Functional Analysis especially due to its extensive applications in random differential as well as random integral equations.
. In fact the study of such spaces received an impetus with the pioneering work of Schweizer and Sklar [3]. The theory of PM spaces is of paramount importance in Probabilistic Functional Analysis especially due to its extensive applications in random differential as well as random integral equations.
Fixed point theory is one of the most fruitful and effective tools in mathematics which has enormous applications within as well as outside mathematics. The theory of fixed points in PM spaces is a part of Probabilistic Analysis which continues to be an active area of mathematical research. By now, several authors have already established numerous fixed point and common fixed point theorems in PM spaces. For an idea of this kind of the literature, one can consult the results contained in [3–14].
In metric spaces, Jungck [15] introduced the notion of compatible mappings and utilized the same (as a tool) to improve commutativity conditions in common fixed point theorems. This concept has been frequently employed to prove existence theorems on common fixed points. However, the study of common fixed points of noncompatible mappings is also equally interesting which was initiated by Pant [16]. Recently, Aamri and Moutawakil [17] and Liu et al. [18] respectively, defined the property (E.A) and the common property (E.A) and proved some common fixed point theorems in metric spaces. Imdad et al. [19] extended the results of Aamri and Moutawakil [17] to semimetric spaces. Most recently, Kubiaczyk and Sharma [20] defined the property (E.A) in PM spaces and used it to prove results on common fixed points wherein authors claim to prove their results for strict contractions which are merely valid up to contractions.
In 2002, Branciari [21] proved a fixed point result for a mapping satisfying an integral-type inequality which is indeed an analogue of contraction mapping condition. In recent past, several authors (e.g., [22–26]) proved various fixed point theorems employing relatively more general integral type contractive conditions. In one of his interesting articles, Suzuki [27] pointed out that Meir-Keeler contractions of integral type are still Meir-Keeler contractions. In this paper, we prove the fixed point theorems for weakly compatible mappings via an implicit relation in Menger PM spaces satisfying the common property (E.A). Our results substantially improve the corresponding theorems contained in [21, 24, 26, 28] along with some other relevant results in Menger as well as metric spaces. Some related results are also derived besides furnishing illustrative examples.
In the following lines, we collect the background material to make our presentation as self-contained as possible.
Definition 1.1 (see [3]).
A mapping  is called distribution function if it is nondecreasing and left continuous with
is called distribution function if it is nondecreasing and left continuous with  and
and  .
.
Let  be the set of all distribution functions whereas
be the set of all distribution functions whereas  be the set of specific distribution function (also known as Heaviside function) defined by
be the set of specific distribution function (also known as Heaviside function) defined by

Definition 1.2 (see [1]).
Let  be a nonempty set. An ordered pair
be a nonempty set. An ordered pair  is called a PM space if
is called a PM space if  is a mapping from
is a mapping from  into
into  satisfying the following conditions:
satisfying the following conditions:
(1) if and only if
if and only if  ,
,
(2)
(3) and
and  , then
, then  , for all
, for all  and
and 
Every metric space  can always be realized as a PM space by considering
can always be realized as a PM space by considering  defined by
defined by  for all
for all  . So PM spaces offer a wider framework (than that of the metric spaces) and are general enough to cover even wider statistical situations.
. So PM spaces offer a wider framework (than that of the metric spaces) and are general enough to cover even wider statistical situations.
Definition 1.3 (see [3]).
A mapping  is called a
is called a  -norm if
-norm if
(1)
(2)
(3) for
for 
(4) for all
for all  .
.
Example 1.4.
The following are the four basic  -norms.
-norms.
(i)The minimum  -norm:
-norm:  .
.
(ii)The product  -norm:
-norm:  .
.
(iii)The Lukasiewicz  -norm:
-norm:  .
.
(iv)The weakest  -norm, the drastic product:
-norm, the drastic product:

In respect of above mentioned  -norms, we have the following ordering:
-norms, we have the following ordering:

Throughout this paper,  stands for an arbitrary continuous
stands for an arbitrary continuous  -norm.
-norm.
Definition 1.5 (see [1]).
A Menger PM space  is a triplet where
is a triplet where  is a PM space and
is a PM space and  is a
is a  -norm satisfying the following condition:
-norm satisfying the following condition:

Definition 1.6 (see [6]).
A sequence  in a Menger PM space
in a Menger PM space  is said to converge to a point
is said to converge to a point  in
in  if for every
if for every  and
and  , there is an integer
, there is an integer  such that
such that  for all
for all  .
.
Definition 1.7 (see [10]).
A pair  of self-mappings of a Menger PM space
of self-mappings of a Menger PM space  is said to be compatible if
is said to be compatible if  for all
for all  , whenever
, whenever  is a sequence in
is a sequence in  such that
such that  for some
for some  in
in  as
as  .
.
Definition 1.8 (see [23]).
A pair  of self-mappings of a Menger PM space
of self-mappings of a Menger PM space  is said to be noncompatible if and only if there exists at least one sequence
is said to be noncompatible if and only if there exists at least one sequence  in
in  such that
such that

but for some  is either less than 1 or nonexistent.
is either less than 1 or nonexistent.
Definition 1.9 (see [6]).
A pair  of self-mappings of a Menger PM space
of self-mappings of a Menger PM space  is said to satisfy the property (E.A) if there exist a sequence
is said to satisfy the property (E.A) if there exist a sequence  in
in  such that
such that

Clearly, a pair of compatible mappings as well as noncompatible mappings satisfies the property (E.A).
Inspired by Liu et al. [18], we introduce the following.
Definition 1.10.
Two pairs  and
and  of self-mappings of a Menger PM space
of self-mappings of a Menger PM space  are said to satisfy the common property (E.A) if there exist two sequences
are said to satisfy the common property (E.A) if there exist two sequences  in
in  and some
and some  in
in  such that
such that

Example 1.11.
Let  be a Menger PM space with
be a Menger PM space with  and,
and,

for all  . Define self-mappings
. Define self-mappings  and
and  on
on  as
as  ,
,  ,
,  , and
, and  for all
for all  . Then with sequences
. Then with sequences  and
and  in
in  , one can easily verify that
, one can easily verify that

This shows that the pairs  and
and  share the common property
share the common property 
Definition 1.12 (see[29]).
A pair  of self-mappings of a nonempty set
of self-mappings of a nonempty set  is said to be weakly compatible if the pair commutes on the set of coincidence points, that is,
is said to be weakly compatible if the pair commutes on the set of coincidence points, that is,  for some
for some  implies that
implies that  .
.
Definition 1.13 (see [8]).
Two finite families of self-mappings  and
and  of a set
of a set  are said to be pairwise commuting if
are said to be pairwise commuting if
(1) ,
,
(2) ,
,
(3) and
and  .
.
2. Implicit Relation
Let  be the set of all continuous functions
be the set of all continuous functions  satisfying the following conditions:
satisfying the following conditions:
 , for all
, for all  ,
,
 , for all
, for all  ,
,
 , for all
, for all  .
.
Example 2.1.
Define  as
as

where  is increasing and continuous function such that
is increasing and continuous function such that  for all
for all  Notice that
Notice that
 , for all
, for all  ,
,
 , for all
, for all  ,
,
 , for all
, for all  .
.
Example 2.2.
Define  as
as

where  is an increasing and continuous function such that
is an increasing and continuous function such that  for all
for all  and
and  is a Lebesgue integrable function which is summable and satisfies
is a Lebesgue integrable function which is summable and satisfies

Observe that
 , for all
, for all  ,
,
 , for all
, for all  ,
,
 , for all
, for all  .
.
Example 2.3.
Define  as
as

where  is an increasing and continuous function such that
is an increasing and continuous function such that  for all
for all  and
and  is a Lebesgue integrable function which is summable and satisfies
is a Lebesgue integrable function which is summable and satisfies

Observe that
 , for all
, for all  ,
,
 , for all
, for all  ,
,
() , for all
, for all  .
.
3. Main Results
We begin with the following observation.
Lemma 3.1.
Let  and
and  be self-mappings of a Menger space
be self-mappings of a Menger space  satisfying the following:
satisfying the following:
(i)the pair  (or
(or  satisfies the property
satisfies the property  ;
;
-
(ii)
for any
 and for all
and for all  ,
, 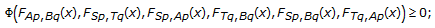 (3.1)
(3.1)
(iii) (or
(or 
Then the pairs  and
and  share the common property
share the common property 
Proof.
Suppose that the pair  owns the property (E.A), then there exists a sequence
owns the property (E.A), then there exists a sequence  in
in  such that
such that

Since  , hence for each
, hence for each  there exists
there exists  such that
such that  Therefore,
Therefore,

Thus in all, we have  and
and  Now we assert that
Now we assert that  . Suppose that
. Suppose that  then applying inequality (3.1), we obtain
then applying inequality (3.1), we obtain

which on making  reduces to
reduces to

or

which is a contradiction to  , and therefore
, and therefore  . Hence the pairs
. Hence the pairs  and
and  share the common property (E.A).
share the common property (E.A).
Remark 3.2.
The converse of Lemma 3.1 is not true in general. For a counter example, one can see Example 3.17 (presented in the end).
Theorem 3.3.
Let  and
and  be self-mappings on a Menger PM space
be self-mappings on a Menger PM space  satisfying inequality (3.1). Suppose that
satisfying inequality (3.1). Suppose that
(i)the pair  (or
(or  enjoys the property (E.A),
enjoys the property (E.A),
(ii) (or
(or 
(iii) (or
(or  is a closed subset of
is a closed subset of  .
.
Then the pairs  and
and  have a point of coincidence each. Moreover,
have a point of coincidence each. Moreover,  and
and  have a unique common fixed point provided that both the pairs
have a unique common fixed point provided that both the pairs  and
and  are weakly compatible.
are weakly compatible.
Proof.
In view of Lemma 3.1, the pairs  and
and  share the common property (E.A), that is, there exist two sequences
share the common property (E.A), that is, there exist two sequences  and
and  in
in  such that
such that

Suppose that  is a closed subset of
is a closed subset of  , then
, then  for some
for some  If
If  , then applying inequality (3.1), we obtain
, then applying inequality (3.1), we obtain

which on making  reduces to
reduces to

which is a contradiction to  . Hence
. Hence 
Since  , there exists
, there exists  such that
such that 
If  , then using inequality (3.1), we have
, then using inequality (3.1), we have

or

which is a contradiction to  , and therefore
, and therefore 
Since the pairs  and
and  are weakly compatible and
are weakly compatible and  therefore
therefore

If  , then using inequality (3.1), we have
, then using inequality (3.1), we have

or

which is a contradiction to  , and therefore
, and therefore 
Similarly, one can prove that  Hence
Hence  , and
, and  is a common fixed point of
is a common fixed point of  and
and  . The uniqueness of common fixed point is an easy consequences of inequality (3.1).
. The uniqueness of common fixed point is an easy consequences of inequality (3.1).
By choosing  and
and  suitably, one can derive corollaries involving two or three mappings. As a sample, we deduce the following natural result for a pair of self-mappings by setting
suitably, one can derive corollaries involving two or three mappings. As a sample, we deduce the following natural result for a pair of self-mappings by setting  and
and  (in Theorem 3.3).
(in Theorem 3.3).
Corollary 3.4.
Let  and
and  be self-mappings on a Menger space
be self-mappings on a Menger space  . Suppose that
. Suppose that
(i)the pair  enjoys the property (E.A),
enjoys the property (E.A),
(ii)for all  and for all
and for all  ,
,

(iii) is a closed subset of
is a closed subset of  .
.
Then  and
and  have a coincidence point. Moreover, if the pair
have a coincidence point. Moreover, if the pair  is weakly compatible, then
is weakly compatible, then  and
and  have a unique common fixed point.
have a unique common fixed point.
Theorem 3.5.
Let  and
and  be self-mappings of a Menger PM space
be self-mappings of a Menger PM space  satisfying the inequality (3.1). Suppose that
satisfying the inequality (3.1). Suppose that
(i)the pairs  and
and  share the common property (E.A),
share the common property (E.A),
(ii) and
and  are closed subsets of
are closed subsets of  .
.
If the pairs  and
and  are weakly compatible, then
are weakly compatible, then  and
and  have a unique common fixed point in
have a unique common fixed point in  .
.
Proof.
Suppose that the pairs  and
and  satisfy the common property (E.A), then there exist two sequences
satisfy the common property (E.A), then there exist two sequences  and
and  in
in  such that
such that

Since  and
and  are closed subsets of
are closed subsets of  , we obtain
, we obtain  for some
for some  .
.
If  then using inequality (3.1), we have
then using inequality (3.1), we have

which on making  reduces to
reduces to

which is a contradiction to  , and hence
, and hence  The rest of the proof can be completed on the lines of the proof of Theorem 3.3, hence it is omitted.
The rest of the proof can be completed on the lines of the proof of Theorem 3.3, hence it is omitted.
Remark 3.6.
Theorem 3.3 extends the main result of Ciric [30] to Menger PM spaces besides extending the main result of Kubiaczyk and Sharma [20] to two pairs of mappings without any condition on containment of ranges amongst involved mappings.
Theorem 3.7.
The conclusions of Theorem 3.5 remain true if condition (ii) of Theorem 3.5 is replaced by the following:
 and
and 
Corollary 3.8.
The conclusions of Theorems 3.3 and 3.5 remain true if conditions (ii) (of Theorem 3.3) and (iii) (of Theorem 3.7) are replaced by the following:
(of Theorem 3.7) are replaced by the following:
(iv) and
and  are closed subsets of
are closed subsets of  whereas
whereas  and
and  .
.
As an application of Theorem 3.3, we prove the following result for four finite families of self-mappings. While proving this result, we utilize Definition 1.13 which is a natural extension of commutativity condition to two finite families of mappings.
Theorem 3.9.
Let  and
and  be four finite families of self-mappings of a Menger PM space
be four finite families of self-mappings of a Menger PM space  with
with  ,
,  and
and  satisfying condition (3.1). If the pairs
satisfying condition (3.1). If the pairs  and
and  share the common property (E.A) and
share the common property (E.A) and  as well as
as well as  are closed subsets of
are closed subsets of  , then
, then
(i)the pair  as well as
as well as  has a coincidence point,
has a coincidence point,
(ii) and
and  have a unique common fixed point provided that the pair of families
have a unique common fixed point provided that the pair of families  and
and  commute pairwise, where
commute pairwise, where  ,
,  ,
,  , and
, and  .
.
Proof.
The proof follows on the lines of Theorem 4.1 according to M. Imdad and J. Ali[31] and Theorem 3.1 according to Imdad et al. [19].
Remark 3.10.
By restricting four families as  and
and  in Theorem 3.9, we can derive improved versions of certain results according to Chugh and Rathi [4], Kutukcu and Sharma [32], Rashwan and Hedar [11], Singh and Jain [14], and some others. Theorem 3.9 also generalizes the main result of Razani and Shirdaryazdi [12] to any finite number of mappings.
in Theorem 3.9, we can derive improved versions of certain results according to Chugh and Rathi [4], Kutukcu and Sharma [32], Rashwan and Hedar [11], Singh and Jain [14], and some others. Theorem 3.9 also generalizes the main result of Razani and Shirdaryazdi [12] to any finite number of mappings.
By setting  and
and  in Theorem 3.9, we deduce the following.
in Theorem 3.9, we deduce the following.
Corollary 3.11.
Let  and
and  be self-mappings of a Menger space
be self-mappings of a Menger space  such that the pairs
such that the pairs  and
and  share the common property (E.A) and also satisfy the condition
share the common property (E.A) and also satisfy the condition

 ,
,  and
and  and
and  are fixed positive integers.
are fixed positive integers.
If  and
and  are closed subsets of
are closed subsets of  , then
, then  and
and  have a unique common fixed point provided,
have a unique common fixed point provided,  and
and  .
.
Remark 3.12.
Corollary 3.11 is a slight but partial generalization of Theorem 3.3 as the commutativity requirements (i.e.,  and
and  ) in this corollary are stronger as compared to weak compatibility in Theorem 3.3. Corollary 3.11 also presents the generalized and improved form of a result according to Bryant [33] in Menger PM spaces.
) in this corollary are stronger as compared to weak compatibility in Theorem 3.3. Corollary 3.11 also presents the generalized and improved form of a result according to Bryant [33] in Menger PM spaces.
Our next result involves a lower semicontinuous function  such that
such that  for all
for all  along with
along with  and
and  .
.
Theorem 3.13.
Let  and
and  be self-mappings of a Menger space
be self-mappings of a Menger space  satisfying conditions (i) and (ii) of Theorem 3.5 and for all
satisfying conditions (i) and (ii) of Theorem 3.5 and for all 

where ,
,  ,
,  ,
,  ,
,  .
.
Then the pairs  and
and  have point of coincidence each. Moreover,
have point of coincidence each. Moreover,  and
and  have a unique common fixed point provided that both the pairs
have a unique common fixed point provided that both the pairs  and
and  are weakly compatible.
are weakly compatible.
Proof.
As both the pairs share the common property  , there exist two sequences
, there exist two sequences  such that
such that

If  is a closed subset of
is a closed subset of  , then (3.21)
, then (3.21) Therefore, there exists a point
Therefore, there exists a point  such that
such that  Now we assert that
Now we assert that  If it is not so, then setting
If it is not so, then setting  in (3.20), we get
in (3.20), we get

which on making  , reduces to
, reduces to

or

a contradiction. Therefore  , and hence
, and hence  which shows that the pair
which shows that the pair  has a point of coincidence.
has a point of coincidence.
If  is a closed subset of
is a closed subset of  , then (3.21)
, then (3.21) Hence, there exists a point
Hence, there exists a point  such that
such that  Now we show that
Now we show that  If it is not so, then using (3.20) with
If it is not so, then using (3.20) with  , we have
, we have

which on making  reduces to
reduces to

or

a contradiction. Therefore  and hence
and hence  which proves that the pair
which proves that the pair  has a point of coincidence.
has a point of coincidence.
Since the pairs  and
and  are weakly compatible and both the pairs have point of coincidence
are weakly compatible and both the pairs have point of coincidence  and
and  , respectively. Following the lines of the proof of Theorem 3.3, one can easily prove the existence of unique common fixed point of mappings
, respectively. Following the lines of the proof of Theorem 3.3, one can easily prove the existence of unique common fixed point of mappings  and
and  . This concludes the proof.
. This concludes the proof.
Remark 3.14.
Theorem 3.13 generalizes the main result of Kohli and Vashistha [9] to two pairs of self-mappings as Theorem 3.13 never requires any condition on the containment of ranges amongst involved mappings besides weakening the completeness requirement of the space to closedness of suitable subspaces along with suitable commutativity requirements of the involved mappings. Here one may also notice that the function  is lower semicontinuous whereas all the involved mappings may be discontinuous at the same time.
is lower semicontinuous whereas all the involved mappings may be discontinuous at the same time.
Remark 3.15.
Notice that results similar to Theorems 3.5 –3.9 and Corollaries 3.4–3.11 can also be outlined in respect of Theorem 3.13, but we omit the details with a view to avoid any repetition.
We conclude this paper with two illustrative examples which demonstrate the validity of the hypotheses of Theorem 3.3 and Theorem 3.13.
Example 3.16.
Let  be a Menger space, where
be a Menger space, where  with a
with a  -norm defined by
-norm defined by  for all
for all  ,
,  for all
for all  and
and

Define  and
and  by:
by: 

Also define  as
as

It is easy to see that for all  and
and 

Also  . Thus all the conditions of Theorem 3.3 are satisfied, and 1 is the unique common fixed point of
. Thus all the conditions of Theorem 3.3 are satisfied, and 1 is the unique common fixed point of  and
and 
Example 3.17.
Let  and
and  be the same as in Example 3.16. Define
be the same as in Example 3.16. Define  and
and  by
by

By a routine calculation, one can verify that for all  and
and 

Also  ,
,  ,
,  . Thus all conditions of Theorem 3.13 are satisfied, and 1 is the unique common fixed point of
. Thus all conditions of Theorem 3.13 are satisfied, and 1 is the unique common fixed point of  and
and 
References
Menger K: Statistical metrics. Proceedings of the National Academy of Sciences of the United States of America 1942, 28: 535–537. 10.1073/pnas.28.12.535
Menger K: Probabilistic geometry. Proceedings of the National Academy of Sciences of the United States of America 1951, 37: 226–229. 10.1073/pnas.37.4.226
Schweizer B, Sklar A: Probabilistic Metric Spaces, North-Holland Series in Probability and Applied Mathematics. North-Holland, New York, NY, USA; 1983:xvi+275.
Chugh R, Rathi S: Weakly compatible maps in probabilistic metric spaces. The Journal of the Indian Mathematical Society 2005,72(1–4):131–140.
Fang J, Gao Y: Common fixed point theorems under strict contractive conditions in Menger spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,70(1):184–193. 10.1016/j.na.2007.11.045
Hadžić O, Pap E: Fixed Point Theory in Probabilistic Metric Spaces, Mathematics and Its Applications. Volume 536. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2001:x+273.
Hicks TL: Fixed point theory in probabilistic metric spaces. Univerzitet u Novom Sadu. Zbornik Radova Prirodno-Matematičkog Fakulteta. Serija za Matemati 1983, 13: 63–72.
Imdad M, Ali J, Tanveer M: Coincidence and common fixed point theorems for nonlinear contractions in Menger PM spaces. Chaos, Solitons and Fractals 2009,42(5):3121–3129. 10.1016/j.chaos.2009.04.017
Kohli JK, Vashistha S: Common fixed point theorems in probabilistic metric spaces. Acta Mathematica Hungarica 2007,115(1–2):37–47. 10.1007/s10474-006-0533-7
Mishra SN: Common fixed points of compatible mappings in PM-spaces. Mathematica Japonica 1991,36(2):283–289.
Rashwan RA, Hedar A: On common fixed point theorems of compatible mappings in Menger spaces. Demonstratio Mathematica 1998,31(3):537–546.
Razani A, Shirdaryazdi M: A common fixed point theorem of compatible maps in Menger space. Chaos, Solitons and Fractals 2007,32(1):26–34. 10.1016/j.chaos.2005.10.096
Sehgal VM, Bharucha-Reid AT: Fixed points of contraction mappings on probabilistic metric spaces. Mathematical Systems Theory 1972, 6: 97–102. 10.1007/BF01706080
Singh B, Jain S: A fixed point theorem in Menger space through weak compatibility. Journal of Mathematical Analysis and Applications 2005,301(2):439–448. 10.1016/j.jmaa.2004.07.036
Jungck G: Compatible mappings and common fixed points. International Journal of Mathematics and Mathematical Sciences 1986,9(4):771–779. 10.1155/S0161171286000935
Pant RP: Common fixed points of noncommuting mappings. Journal of Mathematical Analysis and Applications 1994,188(2):436–440. 10.1006/jmaa.1994.1437
Aamri M, El Moutawakil D: Some new common fixed point theorems under strict contractive conditions. Journal of Mathematical Analysis and Applications 2002,270(1):181–188. 10.1016/S0022-247X(02)00059-8
Liu Y, Wu J, Li Z: Common fixed points of single-valued and multivalued maps. International Journal of Mathematics and Mathematical Sciences 2005,2005(19):3045–3055. 10.1155/IJMMS.2005.3045
Imdad M, Ali J, Khan L: Coincidence and fixed points in symmetric spaces under strict contractions. Journal of Mathematical Analysis and Applications 2006,320(1):352–360. 10.1016/j.jmaa.2005.07.004
Kubiaczyk I, Sharma S: Some common fixed point theorems in Menger space under strict contractive conditions. Southeast Asian Bulletin of Mathematics 2008,32(1):117–124.
Branciari A: A fixed point theorem for mappings satisfying a general contractive condition of integral type. International Journal of Mathematics and Mathematical Sciences 2002,29(9):531–536. 10.1155/S0161171202007524
Aliouche A: A common fixed point theorem for weakly compatible mappings in symmetric spaces satisfying a contractive condition of integral type. Journal of Mathematical Analysis and Applications 2006,322(2):796–802. 10.1016/j.jmaa.2005.09.068
Djoudi A, Aliouche A: Common fixed point theorems of Gregus type for weakly compatible mappings satisfying contractive conditions of integral type. Journal of Mathematical Analysis and Applications 2007,329(1):31–45. 10.1016/j.jmaa.2006.06.037
Rhoades BE: Two fixed-point theorems for mappings satisfying a general contractive condition of integral type. International Journal of Mathematics and Mathematical Sciences 2003, (63):4007–4013.
Turkoglu D, Altun I: A common fixed point theorem for weakly compatible mappings in symmetric spaces satisfying an implicit relation. Boletin de la Sociedad Matematica Mexicana. Tercera Serie 2007,13(1):195–205.
Vijayaraju P, Rhoades BE, Mohanraj R: A fixed point theorem for a pair of maps satisfying a general contractive condition of integral type. International Journal of Mathematics and Mathematical Sciences 2005, (15):2359–2364.
Suzuki T: Meir-Keeler contractions of integral type are still Meir-Keeler contractions. International Journal of Mathematics and Mathematical Sciences 2007, 2007:-6.
Ali J, Imdad M: An implicit function implies several contraction conditions. Sarajevo Journal of Mathematics 2008,4(17)(2):269–285.
Jungck G: Common fixed points for noncontinuous nonself maps on nonmetric spaces. Far East Journal of Mathematical Sciences 1996,4(2):199–215.
Cirić LB: A generalization of Banach's contraction principle. Proceedings of the American Mathematical Society 1974, 45: 267–273.
Imdad M, Ali J: Jungck's common fixed point theorem and E.A property. Acta Mathematica Sinica 2008,24(1):87–94. 10.1007/s10114-007-0990-0
Kutukcu S, Sharma S: Compatible maps and common fixed points in Menger probabilistic metric spaces. Communications of the Korean Mathematical Society 2009,24(1):17–27. 10.4134/CKMS.2009.24.1.017
Bryant VW: A remark on a fixed-point theorem for iterated mappings. The American Mathematical Monthly 1968, 75: 399–400.
Author information
Authors and Affiliations
Corresponding author
Additional information
An erratum to this article is available at http://dx.doi.org/10.1186/1687-1812-2011-28.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Imdad, M., Tanveer, M. & Hasan, M. Some Common Fixed Point Theorems in Menger PM Spaces. Fixed Point Theory Appl 2010, 819269 (2010). https://doi.org/10.1155/2010/819269
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/819269
 and for all
and for all  ,
,