- Research Article
- Open access
- Published:
Equivalent Extensions to Caristi-Kirk's Fixed Point Theorem, Ekeland's Variational Principle, and Takahashi's Minimization Theorem
Fixed Point Theory and Applications volume 2010, Article number: 970579 (2009)
Abstract
With a recent result of Suzuki (2001) we extend Caristi-Kirk's fixed point theorem, Ekeland's variational principle, and Takahashi's minimization theorem in a complete metric space by replacing the distance with a  -distance. In addition, these extensions are shown to be equivalent. When the
-distance. In addition, these extensions are shown to be equivalent. When the  -distance is l.s.c. in its second variable, they are applicable to establish more equivalent results about the generalized weak sharp minima and error bounds, which are in turn useful for extending some existing results such as the petal theorem.
-distance is l.s.c. in its second variable, they are applicable to establish more equivalent results about the generalized weak sharp minima and error bounds, which are in turn useful for extending some existing results such as the petal theorem.
1. Introduction
Let  be a complete metric space and
be a complete metric space and  a proper lower semicontinuous (l.s.c.) bounded below function. Caristi-Kirk fixed point theorem [1, Theorem
a proper lower semicontinuous (l.s.c.) bounded below function. Caristi-Kirk fixed point theorem [1, Theorem  ] states that there exists
] states that there exists  for a relation or multivalued mapping
for a relation or multivalued mapping  if for each
if for each  with
with  there exists
there exists  such that
such that

(see also [2, Theorem  ] or [3, Theorem
] or [3, Theorem  ]) while Ekeland's variational principle (EVP) [4, 5] asserts that for each
]) while Ekeland's variational principle (EVP) [4, 5] asserts that for each  and
and  with
with  there exists
there exists  such that
such that  and
and

EVP has been shown to have many equivalent formulations such as Caristi-Kirk fixed point theorem, the drop theorem [6], the petal theorem [3, Theorem  ], Takahashi minimization theorem [7, Theorem
], Takahashi minimization theorem [7, Theorem  ], and two results about weak sharp minima and error bounds [8, Theorems
], and two results about weak sharp minima and error bounds [8, Theorems  and
and  ]. Moreover, in a Banach space, it is equivalent to the Bishop-Phelps theorem (see [9]). EVP has played an important role in the study of nonlinear analysis, convex analysis, and optimization theory. For more applications, EVP and several equivalent results stated above have been extended by introducing more general distances. For example, Kada et al. have presented the concept of a
]. Moreover, in a Banach space, it is equivalent to the Bishop-Phelps theorem (see [9]). EVP has played an important role in the study of nonlinear analysis, convex analysis, and optimization theory. For more applications, EVP and several equivalent results stated above have been extended by introducing more general distances. For example, Kada et al. have presented the concept of a  -distance in [10] to extend EVP, Caristi's fixed point theorem, and Takahashi minimization theorem. Suzuki has extended these three results by replacing a
-distance in [10] to extend EVP, Caristi's fixed point theorem, and Takahashi minimization theorem. Suzuki has extended these three results by replacing a  -distance with a
-distance with a  -distance in [11]. For more extensions of these theorems, with a
-distance in [11]. For more extensions of these theorems, with a  -distance being replaced by a
-distance being replaced by a  -function and a
-function and a  -function, respectively, the reader is referred to [12, 13].
-function, respectively, the reader is referred to [12, 13].
Theoretically, it is interesting to reveal the relationships among the above existing results (or their extensions). In this paper, while further extending the above theorems in a complete metric space with a  -distance, we show that these extensions are equivalent. For the case where the
-distance, we show that these extensions are equivalent. For the case where the  -distance is l.s.c. in its second variable, we apply our generalizations to extend several existing results about the weak sharp minima and error bounds and then demonstrate their equivalent relationship. In particular, when the
-distance is l.s.c. in its second variable, we apply our generalizations to extend several existing results about the weak sharp minima and error bounds and then demonstrate their equivalent relationship. In particular, when the  -distance reduces to the complete metric, our results turn out to be equivalent to EVP and hence to its existing equivalent formulations.
-distance reduces to the complete metric, our results turn out to be equivalent to EVP and hence to its existing equivalent formulations.
2.  -Distance and
-Distance and  -Distance
-Distance
For convenience, we recall the concepts of  -distance and
-distance and  -distance and some properties which will be used in the paper.
-distance and some properties which will be used in the paper.
Definition 2.1 (see [10]).
Let  be a metric space. A function
be a metric space. A function  is called a
is called a  -distance on
-distance on  if the following are satisfied:
if the following are satisfied:
 for all
for all  ;
;
for each  ,
,  is l.s.c.;
is l.s.c.;
for each  there exists
there exists  such that
such that

From the definition, we see that the metric  is a
is a  -distance on
-distance on  . If
. If  is a normed linear space with norm
is a normed linear space with norm  , then both
, then both  and
and  defined by
defined by

are  -distances on
-distances on  . Note that
. Note that  for each
for each  with
with  . For more examples, we see [10].
. For more examples, we see [10].
It is easy to see that for any  and
and  -distance
-distance  , the function
, the function  is also a
is also a  -distance. For any positive
-distance. For any positive  and
and  -distance
-distance  on
on  , the function
, the function  defined by
defined by

is a bounded  -distance on
-distance on  .
.
The following proposition shows that we can construct another  -distance from a given
-distance from a given  -distance under certain conditions.
-distance under certain conditions.
Proposition 2.2.
Let  ,
,  a
a  -distance on
-distance on  , and
, and  a nondecreasing function. If, for each
a nondecreasing function. If, for each  ,
,

then the function  defined by
defined by

is a  -distance. In particular, if
-distance. In particular, if  is bounded on
is bounded on  , then
, then  is a
is a  -distance.
-distance.
Proof.
Since  is nondecreasing, for
is nondecreasing, for  ,
,

In addition,  is obviously lower semicontinuous in its second variable.
is obviously lower semicontinuous in its second variable.
Now, for each  there exists
there exists  such that
such that

Taking  such that
such that

we obtain that, for  in
in  with
with  and
and  ,
,

from which it follows that  . Similarly, we have
. Similarly, we have  . Thus
. Thus  . Therefore,
. Therefore,  is a
is a  -distance on
-distance on 
Next, if  is bounded on
is bounded on  , then there exists
, then there exists  such that
such that

Thus  is also a
is also a  -distance on
-distance on  .
.
When  is unbounded on
is unbounded on  , the condition in Proposition 2.2 may not be satisfied. However, if
, the condition in Proposition 2.2 may not be satisfied. However, if  is a nondecreasing function satisfying
is a nondecreasing function satisfying

then the function  in Proposition 2.2 is a
in Proposition 2.2 is a  -distance (see [11, Proposition
-distance (see [11, Proposition  ]), a more general distance introduced by Suzuki in [11] as below.
]), a more general distance introduced by Suzuki in [11] as below.
Definition 2.3 (see [11]).
 is said to be a
is said to be a  -distance on
-distance on  provided that
provided that
 for all
for all  and there exists a function
and there exists a function  such that
such that
 and
and  for all
for all  , and
, and  is concave and continuous in its second variable;
is concave and continuous in its second variable;
 and
and  imply
imply

 and
and  imply
imply

 and
and  imply
imply

Suzuki has proved that a  -distance is a
-distance is a  -distance [11, Proposition
-distance [11, Proposition  ]. If a
]. If a  -distance
-distance  satisfies
satisfies  and
and  for
for  , then
, then  (see [11, Lemma
(see [11, Lemma  ]). For more properties of a
]). For more properties of a  -distance, the reader is referred to [11].
-distance, the reader is referred to [11].
3. Fixed Point Theorems
From now on, we assume that  is a complete metric space and
is a complete metric space and  is a proper l.s.c. and bounded below function unless specified otherwise. In this section, mainly motivated by fixed point theorems (for a single-valued mapping) in [10, 11, 14–16], we present two similar results which are applicable to multivalued mapping cases. The following theorem established by Suzuki's in [11] plays an important role in extending existing results from a single-valued mapping to a multivalued mapping.
is a proper l.s.c. and bounded below function unless specified otherwise. In this section, mainly motivated by fixed point theorems (for a single-valued mapping) in [10, 11, 14–16], we present two similar results which are applicable to multivalued mapping cases. The following theorem established by Suzuki's in [11] plays an important role in extending existing results from a single-valued mapping to a multivalued mapping.
Theorem 3.1 (see [11, Proposition  ]).
]).
Let  be a
be a  -distance on
-distance on  . Denote
. Denote

Then for each  with
with  there exists
there exists  such that
such that  In particular, there exists
In particular, there exists  such that
such that  .
.
Based on Theorem 3.1, [11, Theorem  ] asserts that a single-valued mapping
] asserts that a single-valued mapping  has a fixed point
has a fixed point  in
in  when
when  holds for all
holds for all  (which generalizes [10, Theorem
(which generalizes [10, Theorem  ] by replacing a
] by replacing a  -distance with a
-distance with a  -distance). We show that the conclusion can be strengthened under a slightly weaker condition (in which
-distance). We show that the conclusion can be strengthened under a slightly weaker condition (in which  holds on a subset of
holds on a subset of  instead) for a multivalued mapping
instead) for a multivalued mapping 
Theorem 3.2.
Let  be a
be a  -distance on
-distance on  and
and  a multivalued mapping. Suppose that for some
a multivalued mapping. Suppose that for some  there holds
there holds  for each
for each  with
with  . Then there exists
. Then there exists  such that
such that

where 
Proof.
For each  with
with  , the set
, the set

is a nonempty closed subset of  since
since  is lower semicontinuous and
is lower semicontinuous and

for some  . Thus
. Thus  is a complete metric space. By Theorem 3.1, there exists
is a complete metric space. By Theorem 3.1, there exists  such that
such that  . Since
. Since

there exists  such that
such that  . Thus
. Thus  ,
,  , and
, and

Clearly, [8, Thoerem  ] follows as a special case of Theorem 3.2 with
] follows as a special case of Theorem 3.2 with  . In addition, when
. In addition, when  and
and  is a single-valued mapping, Theorem 3.2 contains [11, Theorem
is a single-valued mapping, Theorem 3.2 contains [11, Theorem  ]. The following simple example further shows that Theorem 3.2 is applicable to more cases.
]. The following simple example further shows that Theorem 3.2 is applicable to more cases.
Example 3.3.
Consider the mapping  defined by
defined by

and the function  for
for  . Obviously
. Obviously  . For any
. For any  ,
,  , and
, and  we have
we have

so, applying Theorem 3.2 to the above  and
and  with
with  for
for  , we obtain
, we obtain  as in Theorem 3.2.
as in Theorem 3.2.
Motivated by [16, Theorem  ] and [14, Theorem
] and [14, Theorem  ], we further extend Theorem 3.2 as follows.
], we further extend Theorem 3.2 as follows.
Theorem 3.4.
Let  be a
be a  -distance on
-distance on  and
and  a multivalued mapping. Let
a multivalued mapping. Let  and
and  satisfy
satisfy

for some  . If for each
. If for each  with
with  there exists
there exists  such that
such that

then there exists  such that
such that

where 
Proof.
For each  with
with  , by assumption, there exists
, by assumption, there exists  such that
such that

based on the inequalities  and
and  . Upon applying Theorem 3.2 to the lower semicontinuous function
. Upon applying Theorem 3.2 to the lower semicontinuous function  on
on  which is complete, we arrive at the conclusion.
which is complete, we arrive at the conclusion.
Next result is immediate from Theorem 3.4.
Theorem 3.5.
Let  be a
be a  -distance on
-distance on  ,
,  either nondecreasing or upper semicontinuous
either nondecreasing or upper semicontinuous  , and
, and  a multivalued mapping. If for some
a multivalued mapping. If for some  and each
and each  with
with  there exists
there exists  such that
such that

then there exists  such that
such that

where  with
with

Proof.
For  , define
, define  . Then for the case where
. Then for the case where  is nondecreasing we have
is nondecreasing we have

Thus the conclusion follows from Theorem 3.4.
For the case where  is u.s.c., we define
is u.s.c., we define  by
by  . Since
. Since  is u.s.c.,
is u.s.c.,  is well defined and nondecreasing. Now, for some
is well defined and nondecreasing. Now, for some  and each
and each  with
with  there exists
there exists  satisfying
satisfying

so we can apply the conclusion in the previous paragraph to  to get the same conclusion.
to get the same conclusion.
Remark 3.6.
When  and
and  is a single-valued mapping, Theorem 3.4 reduces to [16, Theorem
is a single-valued mapping, Theorem 3.4 reduces to [16, Theorem  ] while Theorem 3.5 to [16, Theorems
] while Theorem 3.5 to [16, Theorems  and
and  ]. If also
]. If also  for all
for all  , then Theorem 3.5 reduces to [14, Theorem
, then Theorem 3.5 reduces to [14, Theorem  ] (when
] (when  is nondecreasing) and [15, Theorem
is nondecreasing) and [15, Theorem  ] (when
] (when  is upper semicontinuous). In the later case, it also extends [14, Theorem
is upper semicontinuous). In the later case, it also extends [14, Theorem  ].
].
Furthermore, we will see that the relaxation of  from a single-valued mapping (as in several existing results stated before) to a multivalued one (as in Theorems 3.2–3.5) is more helpful for us to obtain more results in the next section.
from a single-valued mapping (as in several existing results stated before) to a multivalued one (as in Theorems 3.2–3.5) is more helpful for us to obtain more results in the next section.
4. Extensions of Ekeland's Variational Principle
As applications of Theorems 3.4 and 3.5, several generalizations of EVP will be presented in this section.
Theorem 4.1.
Let  be a
be a  -distance on
-distance on  ,
,  ,
,  satisfy
satisfy  , and
, and  satisfy
satisfy

for some  . Then there exists
. Then there exists  such that
such that  and
and

Proof.
Take  . Then
. Then  is a nonempty complete metric space. We claim that there must exist
is a nonempty complete metric space. We claim that there must exist  such that
such that

Otherwise for each  the set
the set

would be nonempty and  . As a mapping from
. As a mapping from  to
to  ,
,  satisfies the conditions in Theorem 3.4, so there exists
satisfies the conditions in Theorem 3.4, so there exists  such that
such that  . This is a contradiction.
. This is a contradiction.
Now, for each  , since
, since  and
and  , inequality (4.3) still holds.
, inequality (4.3) still holds.
It is worth noting that  in the above proof is a multivalued mapping to which Theorem 3.4 is directly applicable, in contrast to [11, Theorem
in the above proof is a multivalued mapping to which Theorem 3.4 is directly applicable, in contrast to [11, Theorem  ] and [16, Theorem
] and [16, Theorem  ].
].
From the proof of Theorem 3.5, we see that the function  defined by
defined by

satisfies the condition in Theorem 4.1 when  is a nondecreasing or u.s.c. function. So, based on Theorem 4.1 or Theorem 3.5, we obtain next result (from which [11, Theorem
is a nondecreasing or u.s.c. function. So, based on Theorem 4.1 or Theorem 3.5, we obtain next result (from which [11, Theorem  ] follows by taking
] follows by taking  ).
).
Theorem 4.2.
Let  be a
be a  -distance on
-distance on  ,
,  ,
,  satisfy
satisfy  , and
, and  either nondecreasing or u.s.c.. Denote
either nondecreasing or u.s.c.. Denote

Then there exists  such that
such that  and
and

If also  and
and  , is l.s.c. in its second variable, then there exists
, is l.s.c. in its second variable, then there exists  satisfying the above property and the following inequality:
satisfying the above property and the following inequality:

Proof.
Similar to the proof of Theorem 4.1, the first part of the conclusion can be derived from Theorem 3.5.
Now, let  and
and  l.s.c. in its second variable. Then the set
l.s.c. in its second variable. Then the set

is nonempty and complete. Note that  is nondecreasing and
is nondecreasing and  . Applying the conclusion of the first part to the function
. Applying the conclusion of the first part to the function  on
on  , we obtain
, we obtain  such that
such that

for all  with
with  . For
. For  , we still have the inequality. Otherwise, there would exist
, we still have the inequality. Otherwise, there would exist  such that
such that  and
and

This with  and the triangle inequality yield
and the triangle inequality yield

that is,  , which is a contradiction.
, which is a contradiction.
Remark 4.3.
-
(i)
For the case where
 is nondecreasing, the function
is nondecreasing, the function  in the proof of Theorem 4.2 reduces to
in the proof of Theorem 4.2 reduces to 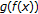 . From the proof we can further see that the nonemptiness and the closedness of
. From the proof we can further see that the nonemptiness and the closedness of  imply the existence of
imply the existence of  in
in 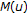 such that
such that 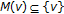 .
. -
(ii)
If we apply Theorem 4.1 directly, then the factor
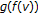 on the right-hand side of the inequality
on the right-hand side of the inequality

in Theorem 4.2 can be replaced with  .
.
-
(iii)
When
 ,
,  is a
is a  -distance on
-distance on 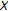 , and
, and  is a nondecreasing function such that
is a nondecreasing function such that

applying Theorem 4.2 to the  -distance
-distance

and  , we arrive at the following conclusion, from which (by taking
, we arrive at the following conclusion, from which (by taking  ) we can obtain [17, Theorem
) we can obtain [17, Theorem  ], a generalization of EVP.
], a generalization of EVP.
Corollary 4.4.
Let  ,
,  a
a  -distance on
-distance on  ,
,  and
and  satisfy
satisfy  and
and  . Let
. Let  be a nondecreasing function such that
be a nondecreasing function such that

Then for each  there exists
there exists  such that
such that 

Note that there exist nondecreasing functions  satisfying
satisfying

For example,  and
and  . Clearly, Corollary 4.4 is not applicable to these examples. For these cases, we present another extension of EVP by using Theorem 4.1 and Proposition 2.2.
. Clearly, Corollary 4.4 is not applicable to these examples. For these cases, we present another extension of EVP by using Theorem 4.1 and Proposition 2.2.
Theorem 4.5.
Let  be a
be a  -distance on
-distance on  ,
,  ,
,  satisfy
satisfy  , and
, and  satisfying
satisfying

for some  . If
. If  is a nondecreasing function and for some
is a nondecreasing function and for some  and each
and each  there holds
there holds

then there exists  such that
such that  and
and

Proof.
Proposition 2.2 shows that the function  defined by
defined by

is a  -distance. Applying Theorem 4.1 to the
-distance. Applying Theorem 4.1 to the  -distance, the desired conclusion follows.
-distance, the desired conclusion follows.
Remark 4.6.
We have obtained Theorem 4.5 from Theorem 4.1. Conversely, when  is a
is a  -distance, Theorem 4.1 follows from Theorem 4.5 by taking
-distance, Theorem 4.1 follows from Theorem 4.5 by taking  for all
for all  . In this case they are equivalent results. If also
. In this case they are equivalent results. If also  holds for some
holds for some  and all
and all  , Theorem 4.5 is obviously applicable. In particular, when we take
, Theorem 4.5 is obviously applicable. In particular, when we take  for certain point
for certain point  , the condition in Theorem 4.5 about
, the condition in Theorem 4.5 about  can be deleted.
can be deleted.
Theorem 4.7.
Let  be a
be a  -distance on
-distance on  ,
,  ,
,  either nondecreasing or u.s.c., and
either nondecreasing or u.s.c., and  nondecreasing. Denote
nondecreasing. Denote

Then for  with
with  and
and

there exists  such that
such that

Proof.
Let  satisfy
satisfy

It is easy to see that  is a bounded
is a bounded  -distance on
-distance on  and hence
and hence

is a  -distance. By Theorem 4.2, there exists
-distance. By Theorem 4.2, there exists  such that
such that

for all  with
with  and
and

from which we obtain  and hence
and hence  . Thus the desired conclusion follows.
. Thus the desired conclusion follows.
Upon taking  and
and  in Theorem 4.7 and replacing
in Theorem 4.7 and replacing  with
with  , we obtain (ii) of [10, Theorem
, we obtain (ii) of [10, Theorem  ], which is also an extension to EVP.
], which is also an extension to EVP.
5. Nonconvex Minimization Theorems
In this section we mainly apply the extensions of EVP obtained in Section 4 to establish minimization theorems which generalize [11, Theorem  ] (an extension to [10, Theorem
] (an extension to [10, Theorem  ] and [7, Theorem
] and [7, Theorem  ]). From these results we also derive Theorem 3.2. Consequently, seven theorems established in Sections 3–5 are shown to be equivalent.
]). From these results we also derive Theorem 3.2. Consequently, seven theorems established in Sections 3–5 are shown to be equivalent.
Firstly, we use Theorem 4.1 to prove the following result.
Theorem 5.1.
Let  be a
be a  -distance on
-distance on  ,
,  , and
, and  satisfy
satisfy

for some  . If for each
. If for each  with
with  there exists
there exists  such that
such that  and
and

then there exists  such that
such that  .
.
Proof.
Denote

Let  (with
(with  ) be fixed. Since
) be fixed. Since  is l.s.c., the set
is l.s.c., the set  is nonempty and complete. Thus, by Theorem 4.1, there exists
is nonempty and complete. Thus, by Theorem 4.1, there exists  such that
such that

The point  must satisfy
must satisfy  . Otherwise, we suppose that
. Otherwise, we suppose that

By the assumption, there exists a point  with
with  such that
such that

which implies  and hence contradicts the inequality
and hence contradicts the inequality

Similarly, we can use Theorem 4.2 to establish the following result.
Theorem 5.2.
Let  be a
be a  -distance on
-distance on  ,
,  , and
, and  either nondecreasing or u.s.c.. If for each
either nondecreasing or u.s.c.. If for each  with
with  there exists
there exists  such that
such that  and
and

then there exists  such that
such that  .
.
Example 5.3.
Consider the function  for
for  . Obviously,
. Obviously,  attains its minimum at
attains its minimum at  . For this simple example, we can also apply Theorem 5.2 to conclude that there exists
. For this simple example, we can also apply Theorem 5.2 to conclude that there exists  such that
such that  since for any
since for any  and each
and each  we have
we have  such that
such that

where  for
for  and
and  .
.
Remark 5.4.
Up to now, beginning with Theorem 3.1, we have established the following results with the proof routes:

As a conclusion in this paper, the following result states that these seven theorems are equivalent.
Theorem 5.5.
Theorems 3.2–3.5, 4.1-4.2, and 5.1-5.2 are all equivalent.
Proof.
By Remark 5.4, it suffices to show that Theorems 5.1-5.2 both imply Theorem 3.2.
Suppose that for some  and for each
and for each  with
with  there exists
there exists  such that
such that  , that is,
, that is,

If there exists  with
with  such that
such that  , then, since there exists
, then, since there exists  such that
such that  ,
,  ,
,  In this case, Theorem 3.2 follows.
In this case, Theorem 3.2 follows.
Next we claim that there must exist  such that
such that

Otherwise, suppose that  for each
for each  with
with  . By Theorem 5.1 or Theorem 5.2 there exists
. By Theorem 5.1 or Theorem 5.2 there exists  such that
such that  . Since
. Since  for
for  , according to the property that
, according to the property that  and
and  imply
imply  ,
,  is a singleton. This implies that there exists
is a singleton. This implies that there exists  such that
such that  and
and  , from which and the triangle inequality we obtain
, from which and the triangle inequality we obtain

This gives  and hence a contradiction to the assumption.
and hence a contradiction to the assumption.
6. Generalized  -Conditions of Takahashi and Hamel
-Conditions of Takahashi and Hamel
The condition in Theorem 5.2 is sufficient for  to attain minimum on
to attain minimum on  . In this section we show that such a condition implies more when the
. In this section we show that such a condition implies more when the  -distance
-distance  (on
(on  ) is l.s.c. in its second variable. For convenience we introduce the following notions.
) is l.s.c. in its second variable. For convenience we introduce the following notions.
Definition 6.1.
A function  is said to satisfy the generalized
is said to satisfy the generalized -condition of Takahashi(Hamel) if for some
-condition of Takahashi(Hamel) if for some  , some nondecreasing function
, some nondecreasing function  , and each
, and each  with
with  there exists
there exists  (
( ) such that
) such that  and
and

where  In particular, for the case
In particular, for the case  the generalized
the generalized  -condition of Takahashi
-condition of Takahashi  Hamel
Hamel is called the generalized condition of Takahashi
is called the generalized condition of Takahashi Hamel
Hamel .
.
When  , the above concepts, respectively, reduce to
, the above concepts, respectively, reduce to  -condition of Takahashi
-condition of Takahashi  Hamel
Hamel and the condition of Takahashi
and the condition of Takahashi  Hamel
Hamel in [8].
in [8].
It is clear that for any  the generalized
the generalized  -condition of Takahashi implies the generalized
-condition of Takahashi implies the generalized  -condition of Takahashi and the generalized
-condition of Takahashi and the generalized  -condition of Hamel implies the generalized
-condition of Hamel implies the generalized  -condition of Hamel. For any
-condition of Hamel. For any  the generalized
the generalized  -condition of Takahashi and the generalized
-condition of Takahashi and the generalized  -condition of Hamel are, respectively, weaker than that of Takahashi and of Hamel. For example, when
-condition of Hamel are, respectively, weaker than that of Takahashi and of Hamel. For example, when  , the function
, the function  satisfies the generalized
satisfies the generalized  -conditions of Takahashi and Hamel for any
-conditions of Takahashi and Hamel for any  but it does not satisfy that of Takahashi nor of Hamel. Furthermore, the generalized
but it does not satisfy that of Takahashi nor of Hamel. Furthermore, the generalized  -condition of Hamel always implies that of Takahashi. Next result asserts that the converse is also true in a complete metric space.
-condition of Hamel always implies that of Takahashi. Next result asserts that the converse is also true in a complete metric space.
Theorem 6.2.
Let  be a
be a  -distance on
-distance on  such that
such that  is l.s.c. on
is l.s.c. on  for each
for each  . For
. For  ,
,  satisfies the generalized
satisfies the generalized  -condition of Takahashi if and only if
-condition of Takahashi if and only if  satisfies the generalized
satisfies the generalized  -condition of Hamel.
-condition of Hamel.
Proof.
The sufficiency is obvious, so it suffices to prove the necessity. Let  satisfy the generalized
satisfy the generalized  -condition of Takahashi and let
-condition of Takahashi and let  be the corresponding nondecreasing function in the definition. Denote
be the corresponding nondecreasing function in the definition. Denote

Then for the case  it suffices to prove that the set
it suffices to prove that the set  is nonempty for each
is nonempty for each  with
with  , where
, where

Let  with
with  be fixed. Since
be fixed. Since  and
and  are both l.s.c., the set
are both l.s.c., the set  is nonempty and complete. Thus, by Theorem 4.1 or Theorem 4.2, there exists
is nonempty and complete. Thus, by Theorem 4.1 or Theorem 4.2, there exists  such that
such that

The point  must be in
must be in  . Otherwise, if
. Otherwise, if  were not in
were not in  , then
, then

By the assumption, there exists a point  with
with  such that
such that

from which and the inequality  we obtain
we obtain

that is,  . And hence
. And hence  This is a contradiction. Therefore,
This is a contradiction. Therefore,  .
.
Next, we suppose that  satisfies the generalized condition of Takahashi. For each
satisfies the generalized condition of Takahashi. For each  , the function
, the function  satisfies the generalized
satisfies the generalized  -condition of Takahashi, so
-condition of Takahashi, so  satisfies the generalized
satisfies the generalized  -condition of Hamel. This implies that
-condition of Hamel. This implies that  is nonempty. For each
is nonempty. For each  with
with  , if
, if  , then
, then  for some
for some  In this case we can find
In this case we can find  such that
such that

If  , then this inequality holds for each
, then this inequality holds for each  . Therefore
. Therefore  satisfies the generalized condition of Hamel.
satisfies the generalized condition of Hamel.
7. Generalized Weak Sharp Minima and Error Bounds
As stated in [8], the  -condition of Takahashi is one of sufficient conditions for an inequality system to have weak sharp minima and error bounds. With Theorem 6.2 being established, the generalized
-condition of Takahashi is one of sufficient conditions for an inequality system to have weak sharp minima and error bounds. With Theorem 6.2 being established, the generalized  -condition of Takahashi plays a similar role for the generalized weak sharp minima and error bounds introduced below.
-condition of Takahashi plays a similar role for the generalized weak sharp minima and error bounds introduced below.
For a proper l.s.c. and bounded below function  we say that
we say that  has generalized local(global) weak sharp minima if the set
has generalized local(global) weak sharp minima if the set  of minimizers of
of minimizers of  on
on  is nonempty and if for some
is nonempty and if for some  and some nondecreasing function
and some nondecreasing function  and each
and each  with
with  there holds
there holds

where 
Due to the equivalence stated in Theorem 6.2, the generalized  -condition of Takahashi is sufficient for
-condition of Takahashi is sufficient for  to have generalized local (global) weak sharp minima.
to have generalized local (global) weak sharp minima.
Theorem 7.1.
Let  be a
be a  -distance on
-distance on  such that
such that  is l.s.c. on
is l.s.c. on  for each
for each  . If, for some
. If, for some  ,
,  satisfies the generalized
satisfies the generalized  -condition of Takahashi, then the set
-condition of Takahashi, then the set  of minimizers of
of minimizers of  on
on  is nonempty and for every
is nonempty and for every  with
with  and each
and each  there holds
there holds

Proof.
The proof is immediate from Theorem 6.2.
For an l.s.c. function  denote
denote

We say that  (or
(or  ) has a generalized local error bound if there exist
) has a generalized local error bound if there exist  and a nondecreasing function
and a nondecreasing function  such that
such that

where  The function
The function  is said to have a generalized global error bound if the above statement is true for
is said to have a generalized global error bound if the above statement is true for  .
.
When  and
and  , the study of generalized error bounds has received growing attention in the mathematical programming (see [18] and the references therein). Now, using Theorem 7.1, we present the following sufficient condition for an l.s.c. inequality system to have generalized error bounds.
, the study of generalized error bounds has received growing attention in the mathematical programming (see [18] and the references therein). Now, using Theorem 7.1, we present the following sufficient condition for an l.s.c. inequality system to have generalized error bounds.
Theorem 7.2.
Let  be a
be a  -distance on
-distance on  such that
such that  is l.s.c. on
is l.s.c. on  for each
for each  and
and  be a proper l.s.c. function. Let
be a proper l.s.c. function. Let  and
and  be a nondecreasing function. Suppose for each
be a nondecreasing function. Suppose for each  the set
the set  is nonempty and for each
is nonempty and for each  there exists a point
there exists a point  such that
such that  and
and

Then  is nonempty and
is nonempty and

Proof.
Let  be given. Since
be given. Since  is l.s.c. and bounded below with
is l.s.c. and bounded below with  and
and  by Theorem 7.1, it suffices to prove
by Theorem 7.1, it suffices to prove

that is,  This must be true. Otherwise, if
This must be true. Otherwise, if  then for
then for  the set
the set  would be empty. This contradicts the assumption.
would be empty. This contradicts the assumption.
Remark 7.3.
Note that the nonemptiness of  in Theorem 7.2 is not a part of assumption but a part of conclusion. In addition, the condition in Theorem 7.2 implies that
in Theorem 7.2 is not a part of assumption but a part of conclusion. In addition, the condition in Theorem 7.2 implies that  satisfies the generalized
satisfies the generalized  -condition of Takahashi, that is,
-condition of Takahashi, that is,

for each  with
with  However, once
However, once  is nonempty, there exists
is nonempty, there exists  such that
such that  as stated below.
as stated below.
Theorem 7.4.
Let  be a
be a  -distance such that
-distance such that  is l.s.c. on
is l.s.c. on  for each
for each  and
and  be a nondecreasing function. Denote
be a nondecreasing function. Denote

Then for each  with
with  there exists
there exists  such that
such that  In particular, there exists
In particular, there exists  such that
such that  .
.
Proof.
Since both  and
and  are l.s.c., for
are l.s.c., for  with
with  ,
,  is nonempty complete metric space. Suppose that for each
is nonempty complete metric space. Suppose that for each  there held
there held  . Then for each
. Then for each  there exists
there exists  such that
such that  . Define
. Define

and denote  . Then
. Then

By Theorem 7.2, the set  is nonempty.
is nonempty.
Now for  , since
, since  (no matter whether
(no matter whether  or
or  ), there exists
), there exists  such that
such that  and
and

from which we obtain  and
and  . Similarly, we have
. Similarly, we have  such that
such that  and
and  . This, with
. This, with  implies
implies  . Thus
. Thus  , which is a contradiction.
, which is a contradiction.
Remark 7.5.
When  and
and  is a
is a  -distance such that
-distance such that  is l.s.c. on
is l.s.c. on  for each
for each  , we can obtain Theorem 3.1 by applying Theorem 7.4 to the function
, we can obtain Theorem 3.1 by applying Theorem 7.4 to the function  . As more applications, the following two propositions are immediate from Theorem 7.4 by taking
. As more applications, the following two propositions are immediate from Theorem 7.4 by taking  ,
,  and
and  , respectively, on
, respectively, on  .
.
Proposition 7.6.
Let  be a complete nonempty subset of a metric space
be a complete nonempty subset of a metric space  ,
,  ,
,  , and let
, and let  be a
be a  -distance on
-distance on  such that
such that  is l.s.c. on
is l.s.c. on  for each
for each  . Denote
. Denote

Suppose that  is nonempty for some
is nonempty for some  . If
. If  for all
for all  , then there exists
, then there exists  such that
such that

Proposition 7.7.
Let  be a complete nonempty subset of a metric space
be a complete nonempty subset of a metric space  ,
,  ,
,  , and let
, and let  be a
be a  -distance on
-distance on  . Denote
. Denote

Suppose that  is l.s.c. in its both variables and
is l.s.c. in its both variables and  is nonempty for some
is nonempty for some  . If
. If  for all
for all  , then there exists
, then there exists  such that
such that  In particular, if
In particular, if  and
and  for all
for all  , then there exists
, then there exists  such that
such that  and
and

Remark 7.8.
Upon taking  in Propositions 7.6 and 7.7, we obtain [3, Theorem
in Propositions 7.6 and 7.7, we obtain [3, Theorem  ] which is equivalent to EVP in a complete metric space. In this case EVP implies Theorem 3.1.
] which is equivalent to EVP in a complete metric space. In this case EVP implies Theorem 3.1.
Finally, following the statement in Theorem 5.5, on the condition that the  -distance
-distance  is l.s.c. on
is l.s.c. on  for each
for each  , Theorems 3.1–3.5, 4.1-4.2, 5.1-5.2, 6.2, and 7.1–7.4 turn out to be equivalent since we have further shown that
, Theorems 3.1–3.5, 4.1-4.2, 5.1-5.2, 6.2, and 7.1–7.4 turn out to be equivalent since we have further shown that

in Sections 6 and 7. In particular, each theorem stated above is equivalent to Theorem 4.5 (as stated in Remark 4.6) when  is a
is a  -distance on
-distance on  , to [3, Theorem
, to [3, Theorem  ] and EVP when
] and EVP when  (see Remark 7.8), and to the Bishop-Phelps Theorem in a Banach space when
(see Remark 7.8), and to the Bishop-Phelps Theorem in a Banach space when  is the corresponding norm. Therefore, we can conclude our paper as below.
is the corresponding norm. Therefore, we can conclude our paper as below.
Theorem 7.9.
Let  be a complete metric space and
be a complete metric space and  a
a  -distance on
-distance on  such that
such that  is l.s.c. for each
is l.s.c. for each  . Then
. Then
(i)Theorems 3.1–3.5, 4.1-4.2, 5.1-5.2, 6.2, and 7.1-7.4 are all equivalent;
(ii)when  is a
is a  -distance on
-distance on  , each theorem in (i) is equivalent to Theorem 4.5;
, each theorem in (i) is equivalent to Theorem 4.5;
(iii)when  , each theorem in (i) is equivalent to EVP.
, each theorem in (i) is equivalent to EVP.
References
Caristi J: Fixed point theorems for mappings satisfying inwardness conditions. Transactions of the American Mathematical Society 1976, 215: 241–251.
Aubin J-P, Siegel J: Fixed points and stationary points of dissipative multivalued maps. Proceedings of the American Mathematical Society 1980,78(3):391–398. 10.1090/S0002-9939-1980-0553382-1
Penot J-P: The drop theorem, the petal theorem and Ekeland's variational principle. Nonlinear Analysis: Theory, Methods & Applications 1986,10(9):813–822. 10.1016/0362-546X(86)90069-6
Ekeland I: On the variational principle. Journal of Mathematical Analysis and Applications 1974, 47: 324–353. 10.1016/0022-247X(74)90025-0
Ekeland I: Nonconvex minimization problems. Bulletin of the American Mathematical Society 1979,1(3):443–474. 10.1090/S0273-0979-1979-14595-6
Danes J: A geometric theorem useful in nonlinear functional analysis. Bollettino della Unione Matematica Italiana 1972, 6: 369–375.
Takahashi W: Existence theorems generalizing fixed point theorems for multivalued mappings. In Fixed Point Theory and Applications, Pitman Research Notes in Mathematics Series. Volume 252. Edited by: Théra MA, Baillon JB. Longman Scientific & Technical, Harlow, UK; 1991:397–406.
Wu Z: Equivalent formulations of Ekeland's variational principle. Nonlinear Analysis: Theory, Methods & Applications 2003,55(5):609–615. 10.1016/j.na.2003.07.009
Borwein JM, Zhu QJ: Techniques of Variational Analysis. Springer, New York, NY, USA; 2005:vi+362.
Kada O, Suzuki T, Takahashi W: Nonconvex minimization theorems and fixed point theorems in complete metric spaces. Mathematica Japonica 1996,44(2):381–391.
Suzuki T: Generalized distance and existence theorems in complete metric spaces. Journal of Mathematical Analysis and Applications 2001,253(2):440–458. 10.1006/jmaa.2000.7151
Lin L-J, Du W-S: Ekeland's variational principle, minimax theorems and existence of nonconvex equilibria in complete metric spaces. Journal of Mathematical Analysis and Applications 2006,323(1):360–370. 10.1016/j.jmaa.2005.10.005
Al-Homidan S, Ansari QH, Yao J-C: Some generalizations of Ekeland-type variational principle with applications to equilibrium problems and fixed point theory. Nonlinear Analysis: Theory, Methods & Applications 2008,69(1):126–139. 10.1016/j.na.2007.05.004
Bae JS: Fixed point theorems for weakly contractive multivalued maps. Journal of Mathematical Analysis and Applications 2003,284(2):690–697. 10.1016/S0022-247X(03)00387-1
Bae JS, Cho EW, Yeom SH: A generalization of the Caristi-Kirk fixed point theorem and its applications to mapping theorems. Journal of the Korean Mathematical Society 1994,31(1):29–48.
Suzuki T: Generalized Caristi's fixed point theorems by Bae and others. Journal of Mathematical Analysis and Applications 2005,302(2):502–508. 10.1016/j.jmaa.2004.08.019
Zhong C-K: On Ekeland's variational principle and a minimax theorem. Journal of Mathematical Analysis and Applications 1997,205(1):239–250. 10.1006/jmaa.1996.5168
Ng KF, Zheng XY: Error bounds for lower semicontinuous functions in normed spaces. SIAM Journal on Optimization 2001,12(1):1–17. 10.1137/S1052623499358884
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wu, Z. Equivalent Extensions to Caristi-Kirk's Fixed Point Theorem, Ekeland's Variational Principle, and Takahashi's Minimization Theorem. Fixed Point Theory Appl 2010, 970579 (2009). https://doi.org/10.1155/2010/970579
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/970579
 -Distance and
-Distance and  -Distance
-Distance is nondecreasing, the function
is nondecreasing, the function  in the proof of Theorem 4.2 reduces to
in the proof of Theorem 4.2 reduces to 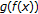 . From the proof we can further see that the nonemptiness and the closedness of
. From the proof we can further see that the nonemptiness and the closedness of  imply the existence of
imply the existence of  in
in 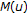 such that
such that 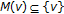 .
.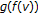 on the right-hand side of the inequality
on the right-hand side of the inequality ,
,  is a
is a  -distance on
-distance on 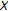 , and
, and  is a nondecreasing function such that
is a nondecreasing function such that -Conditions of Takahashi and Hamel
-Conditions of Takahashi and Hamel