- Research Article
- Open access
- Published:
A Method for a Solution of Equilibrium Problem and Fixed Point Problem of a Nonexpansive Semigroup in Hilbert's Spaces
Fixed Point Theory and Applications volume 2011, Article number: 208434 (2011)
Abstract
We introduce a viscosity approximation method for finding a common element of the set of solutions for an equilibrium problem involving a bifunction defined on a closed, convex subset and the set of fixed points for a nonexpansive semigroup on another one in Hilbert's spaces.
1. Introduction
Let  be a nonempty, closed, and convex subset of a real Hilbert space
be a nonempty, closed, and convex subset of a real Hilbert space  . Denote the metric projection from
. Denote the metric projection from  onto
onto  by
by  . Let
. Let  be a nonexpansive mapping on
be a nonexpansive mapping on  , that is,
, that is,  and
and  , for all
, for all  . We use
. We use  to denote the set of fixed points of
to denote the set of fixed points of  , that is,
, that is,  .
.
Let  be a nonexpansive semigroup on a closed convex subset
be a nonexpansive semigroup on a closed convex subset  , that is,
, that is,
(1)for each  ,
,  is a nonexpansive mapping on
is a nonexpansive mapping on  ,
,
(2) for all
for all  ,
,
(3) for all
for all  ,
,
(4)for each  , the mapping
, the mapping  from
from  into
into  is continuous.
is continuous.
Denote by  . We know [1, 2] that
. We know [1, 2] that  is a closed, convex subset in
is a closed, convex subset in  and
and  if
if  is bounded.
is bounded.
The equilibrium problem is for a bifunction  defined on
defined on  to find
to find  such that
such that

Assume that the bifunction  satisfies the following set of standard properties:
satisfies the following set of standard properties:
(A1) , for all
, for all  ,
,
(A2) for all
for all  ,
,
(A3)for every  ,
,  is weakly lower semicontinuous and convex,
is weakly lower semicontinuous and convex,
(A4) , for all
, for all  .
.
Denote the set of solutions of (1.1) by  . We also know [3] that
. We also know [3] that  is a closed convex subset in
is a closed convex subset in  .
.
The problem studied in this paper is formulated as follows. Let  and
and  be closed convex subsets in
be closed convex subsets in  . Let
. Let  be a bifunction satisfying conditions (A1)–(A4) with
be a bifunction satisfying conditions (A1)–(A4) with  replaced by
replaced by  and let
and let  be a nonexpansive semigroup on
be a nonexpansive semigroup on  . Find an element
. Find an element

where  and
and  denote the set of solutions of an equilibrium problem involving by a bifunction
denote the set of solutions of an equilibrium problem involving by a bifunction  on
on  and the fixed point set of a nonexpansive semigroup
and the fixed point set of a nonexpansive semigroup  on a closed convex subset
on a closed convex subset  , respectively.
, respectively.
In the case that  ,
,  ,
,  , and
, and  , a nonexpansive mapping on
, a nonexpansive mapping on  , for all
, for all  , (1.2) is the fixed point problem of a nonexpansive mapping. In 2000, Moudafi [4] proved the following strong convergence theorem.
, (1.2) is the fixed point problem of a nonexpansive mapping. In 2000, Moudafi [4] proved the following strong convergence theorem.
Theorem 1.1.
Let  be a nonempty, closed, convex subset of a Hilbert space
be a nonempty, closed, convex subset of a Hilbert space  and let
and let  be a nonexpansive mapping on
be a nonexpansive mapping on  such that
such that  . Let
. Let  be a contraction on
be a contraction on  and let
and let  be a sequence generated by:
be a sequence generated by:  and
and

where  satisfies
satisfies

Then,  converges strongly to
converges strongly to  , where
, where  .
.
Such a method for approximation of fixed points is called the viscosity approximation method. It has been developed by Chen and Song [5] to find  , the set of fixed points for a semigroup
, the set of fixed points for a semigroup  on
on  . They proposed the following algorithm:
. They proposed the following algorithm:  and
and

where  , is a contraction,
, is a contraction,  and
and  are sequences of positive real numbers satisfying the conditions:
are sequences of positive real numbers satisfying the conditions:  ,
,  , and
, and  as
as  .
.
Recently, Yao and Noor [6] proposed a new viscosity approximation method

where  ,
,  , and
, and  are in
are in  ,
,  , for finding
, for finding  , when
, when  satisfies the uniformly asymptotically regularity condition
satisfies the uniformly asymptotically regularity condition

uniformly in  , and
, and  is any bounded subset of
is any bounded subset of  . Further, Plubtieng and Pupaeng in [7] studied the following algorithm:
. Further, Plubtieng and Pupaeng in [7] studied the following algorithm:

where  and
and  are in
are in  satisfying the following conditions:
satisfying the following conditions:  ,
,  ,
,  , and
, and  is a positive divergent real sequence.
is a positive divergent real sequence.
There were some methods proposed to solve equilibrium problem (1.1); see for instance [8–12]. In particular, Combettes and Histoaga [3] proposed several methods for solving the equilibrium problem.
In 2007, S. Takahashi and W. Takahashi [13] combinated the Moudafi's method with the Combettes and Histoaga's result in [3] to find an element  . They proved the following strong convergence theorem.
. They proved the following strong convergence theorem.
Theorem 1.2.
Let  be a nonempty, closed, convex subset of a Hilbert space
be a nonempty, closed, convex subset of a Hilbert space  , let
, let  be a nonexpansive mapping on
be a nonexpansive mapping on  and let
and let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4) such that
satisfying (A1)–(A4) such that  . Let
. Let  be a contraction on
be a contraction on  and let
and let  and
and  be sequences generated by:
be sequences generated by:  and
and

where  and
and  satisfy
satisfy

Then,  and
and  converge strongly to
converge strongly to  , where
, where  .
.
Very recently, Ceng and Wong in [14] combined algorithm (1.6) with the result in [3] to propose the following procudure:

for finding an element  in the case that
in the case that  under the uniformly asymptotic regularity condition on the nonexpansive semigroup
under the uniformly asymptotic regularity condition on the nonexpansive semigroup  on
on  .
.
In this paper, motivated by the above results, to solve (1.2), we introduce the following algorithm:

where  is a contraction on
is a contraction on  , that is,
, that is,  and
and  , for all
, for all  ,
,  ,
,

for all  ,
,  ,
,  , and
, and  be the sequences in (0,1), and
be the sequences in (0,1), and  ,
,  are the sequences in
are the sequences in  satisfy the following conditions:
satisfy the following conditions:
(i) ,
,
(ii) ,
,  ,
,
(iii) ,
,
(iv) with bounded
with bounded  ,
,
(v) and
and  .
.
The strong convergence of (1.12)-(1.13) and its corollaries are showed in the next section.
2. Main Results
We formulate the following facts needed in the proof of our results.
Lemma 2.1.
Let  be a real Hilbert space
be a real Hilbert space  . There holds the following identity:
. There holds the following identity:

Lemma 2.2 (see [15]).
Let  be a nonempty, closed, convex subset of a real Hilbert space
be a nonempty, closed, convex subset of a real Hilbert space  . For any
. For any  , there exists a unique
, there exists a unique  such that
such that  , for all
, for all  , and
, and  if and only if
if and only if  for all
for all  .
.
Lemma 2.3 (see [16]).
Let  be a sequence of nonnegative real numbers satisfying the following condition:
be a sequence of nonnegative real numbers satisfying the following condition:

where  and
and  are sequences of real numbers such that
are sequences of real numbers such that  ,
,  , and
, and  . Then,
. Then,  .
.
Lemma 2.4 (see [9]).
Let  be a nonempty, closed, convex subset of
be a nonempty, closed, convex subset of  and
and  be a bifunction of
be a bifunction of  into
into  satisfying the conditions (A1)–(A4). Let
satisfying the conditions (A1)–(A4). Let  and
and  . Then, there exists
. Then, there exists  such that
such that

Lemma 2.5 (see [9]).
Assume that  satisfies the conditions (A1)–(A4). For
satisfies the conditions (A1)–(A4). For  and
and  , define a mapping
, define a mapping  as follows:
as follows:

Then, the following statements hold:
(i) is single-valued,
is single-valued,
(ii) is firmly nonexpansive, that is, for any
is firmly nonexpansive, that is, for any  ,
,

(iii) ,
,
(iv) is closed and convex.
is closed and convex.
Lemma 2.6 (see [17]).
Let  be a nonempty bounded closed convex subset in a real Hilbert space
be a nonempty bounded closed convex subset in a real Hilbert space  and let
and let  be a nonexpansive semigroup on
be a nonexpansive semigroup on  . Then, for any
. Then, for any  ,
,

Lemma 2.7 (Demiclosedness Principle [18]).
If  is a closed convex subset of
is a closed convex subset of  ,
,  is a nonexpansive mapping on
is a nonexpansive mapping on  ,
,  is a sequence in
is a sequence in  such that
such that  and
and  , then
, then  .
.
Lemma 2.8 (see [19]).
Let  and
and  be bounded sequences in a Banach space
be bounded sequences in a Banach space  and
and  be a sequence in
be a sequence in  with
with  . Suppose
. Suppose  for all
for all  and
and  . Then,
. Then,  .
.
Now, we are in a position to prove the following result.
Theorem 2.9.
Let  and
and  be two nonempty, closed, convex subsets in a real Hilbert space
be two nonempty, closed, convex subsets in a real Hilbert space  . Let
. Let  be a bifunction from
be a bifunction from  to
to  satisfying conditions (A1)–(A4) with
satisfying conditions (A1)–(A4) with  replaced by
replaced by  , let
, let  be a nonexpansive semigroup on
be a nonexpansive semigroup on  such that
such that  and let
and let  be a contraction of
be a contraction of  into itself. Then,
into itself. Then,  and
and  generated by (1.12)-(1.13) converge strongly to
generated by (1.12)-(1.13) converge strongly to  , where
, where  .
.
Proof.
Let  . Then,
. Then,  is a contraction of
is a contraction of  into itself. In fact, from
into itself. In fact, from  for all
for all  and the nonexpansive property of
and the nonexpansive property of  for a closed convex subset
for a closed convex subset  in
in  , it implies that
, it implies that

Hence,  is a contraction of
is a contraction of  into itself. Since
into itself. Since  is complete, there exists a unique element
is complete, there exists a unique element  such that
such that  . Such a
. Such a  is an element of
is an element of  , because
, because  .
.
By Lemma 2.4,  and
and  are well defined. For each
are well defined. For each  , by putting
, by putting  and using (ii) and (iii) in Lemma 2.5, we have that
and using (ii) and (iii) in Lemma 2.5, we have that

Put  . Clearly,
. Clearly,  . Suppose that
. Suppose that  . Then, we have, from the nonexpansive property of
. Then, we have, from the nonexpansive property of  , condition (i) and (2.8), that
, condition (i) and (2.8), that

So,  for all
for all  and hence
and hence  is bounded. Therefore,
is bounded. Therefore,  ,
,  , and
, and  are also bounded.
are also bounded.
Next, we show that  as
as  . For this purpose, we define a sequence
. For this purpose, we define a sequence  by
by

Then, we observe that

and, hence,

Now, we estimate the value  by using
by using  and
and  . We have from (2.4) that
. We have from (2.4) that


Putting  in (2.13) and
in (2.13) and  in (2.14), adding the one to the other obtained result and using (A2), we obtain that
in (2.14), adding the one to the other obtained result and using (A2), we obtain that

and, hence,

Without loss of generality, let us assume that there exists a real number  such that
such that  for all
for all  . Then, we have
. Then, we have

and, hence,

On the other hand,

So, we get from (2.10), (2.12), (2.18), (2.19), and the nonexpansive property of  that
that

So,

and by Lemma 2.8, we have

Consequently, it follows from (2.10) and condition (iii) that

By (2.18), (2.23), and

we also obtain

We have, for every  , from (iii) in Lemma 2.5, that
, from (iii) in Lemma 2.5, that

and, hence,

Therefore, from the convexity of  and condition (i), we have
and condition (i), we have

and, hence,

Without loss of generality, we assume that  for all
for all  . Then, for sufficiently large
. Then, for sufficiently large  ,
,

So, we have

Further, since  , by condition (i), (2.19) and
, by condition (i), (2.19) and

we obtain that

Then, from (2.25), (2.33) and the conditions on  and
and  , it implies that
, it implies that

and so

Since

we obtain from (2.31) that

Next, we show that

We choose a subsequence  of the sequence
of the sequence  such that
such that

As  is bounded, there exists a subsequence
is bounded, there exists a subsequence  of the sequence
of the sequence  which converges weakly to
which converges weakly to  . From (2.37), we also have that
. From (2.37), we also have that  converges weakly to
converges weakly to  . Since
. Since  and
and  and
and  ,
,  are two closed convex subsets in
are two closed convex subsets in  , we have that
, we have that  .
.
First, we prove that  . From (2.4) it follows that
. From (2.4) it follows that

and, hence, by using condition (A2), we get

Therefore,

This together with condition (A3) and (2.31) imply that

So,  for all
for all  . It means that
. It means that  .
.
Next we show that  . Since
. Since  , we have
, we have

and, hence, from (2.31) it follows that

Thus, (2.37) together with (2.45) imply

Therefore,  also converges weakly to
also converges weakly to  , as
, as  .
.
On the other hand, for each  , we have that
, we have that

Let  . Since
. Since  , we have from (2.33) that
, we have from (2.33) that

So,  is a nonempty bounded closed convex subset. It is easy to verify that
is a nonempty bounded closed convex subset. It is easy to verify that  is a nonexpansive semigroup on
is a nonexpansive semigroup on  . By Lemma 2.6, we get
. By Lemma 2.6, we get

for every fixed  , and hence, by (2.45)–(2.47), we obtain
, and hence, by (2.45)–(2.47), we obtain

for each  . By Lemma 2.7,
. By Lemma 2.7,  for all
for all  , because
, because  for any mapping
for any mapping  . It means that
. It means that  . Therefore,
. Therefore,  . Since
. Since  , we have from Lemma 2.2 that
, we have from Lemma 2.2 that

So, (2.38) is proved. Further, since  , by using Lemma 2.1, we have that
, by using Lemma 2.1, we have that

This with (2.8) implies that

where

Using Lemma 2.3, we get

From (2.33) it follows that  as
as  . This completes the proof.
. This completes the proof.
Remarks 2.
-
(a)
Note that the following parameters
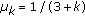 ,
,  ,
, 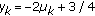 ,
,  for any fixed number
for any fixed number 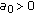 , and
, and 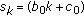 with
with 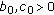 for all
for all 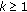 satisfy all conditions in Theorem 2.9.
satisfy all conditions in Theorem 2.9. -
(b)
If
 for all
for all  and
and 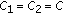 , then we have the following corollary.
, then we have the following corollary.
Corollary 2.10.
Let  be a nonempty, closed, convex subsets in a real Hilbert space
be a nonempty, closed, convex subsets in a real Hilbert space  . Let
. Let  be a bifunction from
be a bifunction from  to
to  satisfying conditions (A1)–(A4), let
satisfying conditions (A1)–(A4), let  be a nonexpansive mapping on
be a nonexpansive mapping on  such that
such that  and let
and let  be a contraction of
be a contraction of  into itself. Let
into itself. Let  and
and  be sequences generated by
be sequences generated by  and
and

where  ,
,  ,
,  , and
, and  satisfy conditions (i)–(v). Then,
satisfy conditions (i)–(v). Then,  and
and  converge strongly to
converge strongly to  , where
, where  .
.
Proof.
From the proof of the theorem,  in (2.12).
in (2.12).
-
(c)
In the case that
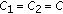 , a closed convex subset in
, a closed convex subset in 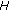 ,
,  for all
for all 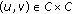 , we have the following result.
, we have the following result.
Corollary 2.11.
Let  be a nonempty, closed, convex subsets in a real Hilbert space
be a nonempty, closed, convex subsets in a real Hilbert space  . Let
. Let  be a nonexpansive semigroup on
be a nonexpansive semigroup on  such that
such that  and let
and let  be a contraction of
be a contraction of  into itself. Let
into itself. Let  and
and  be sequences generated by
be sequences generated by  and
and

where  is defined by (1.13) for all
is defined by (1.13) for all  and
and  ,
,  ,
,  , and
, and  satisfy conditions (i)–(v). Then, the sequences
satisfy conditions (i)–(v). Then, the sequences  and
and  converge strongly to
converge strongly to  , where
, where  .
.
Proof.
By Lemma 2.2,  if and only if
if and only if

Clearly, in addition, if  is a contraction of
is a contraction of  into itself and
into itself and  , then we obtain the algoritm
, then we obtain the algoritm

where  is defined by (1.13) and
is defined by (1.13) and  ,
,  ,
,  , and
, and  satisfy conditions (i)–(v). This algorithm is different from Yao and Noor's algorithm (1.6), in which
satisfy conditions (i)–(v). This algorithm is different from Yao and Noor's algorithm (1.6), in which  for all
for all  . It likes completely the Plubtieng and Punpaeng's algorithm (1.8), but converges under a new condition on
. It likes completely the Plubtieng and Punpaeng's algorithm (1.8), but converges under a new condition on  .
.
References
Browder FE: Fixed-point theorems for noncompact mappings in Hilbert space. Proceedings of the National Academy of Sciences of the United States of America 1965, 53: 1272–1276. 10.1073/pnas.53.6.1272
DeMarr R: Common fixed points for commuting contraction mappings. Pacific Journal of Mathematics 1963, 13: 1139–1141.
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. Journal of Nonlinear and Convex Analysis 2005,6(1):117–136.
Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000,241(1):46–55. 10.1006/jmaa.1999.6615
Chen R, Song Y: Convergence to common fixed point of nonexpansive semigroups. Journal of Computational and Applied Mathematics 2007,200(2):566–575. 10.1016/j.cam.2006.01.009
Yao Y, Noor MA: On viscosity iterative methods for variational inequalities. Journal of Mathematical Analysis and Applications 2007,325(2):776–787. 10.1016/j.jmaa.2006.01.091
Plubtieng S, Punpaeng R: Fixed-point solutions of variational inequalities for nonexpansive semigroups in Hilbert spaces. Mathematical and Computer Modelling 2008,48(1–2):279–286. 10.1016/j.mcm.2007.10.002
Antipin AS: Equilibrium programming: proximal methods. Computational Mathematics and Mathematical Physics 1997,37(11):1285–1296.
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994,63(1–4):123–145.
Mastroeni G: Gap functions for equilibrium problems. Journal of Global Optimization 2003,27(4):411–426. 10.1023/A:1026050425030
Chadli O, Konnov IV, Yao JC: Descent methods for equilibrium problems in a Banach space. Computers & Mathematics with Applications 2004,48(3–4):609–616. 10.1016/j.camwa.2003.05.011
Konnov IV, Pinyagina OV: D-gap functions and descent methods for a class of monotone equilibrium problems. Lobachevskii Journal of Mathematics 2003, 13: 57–65.
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,331(1):506–515. 10.1016/j.jmaa.2006.08.036
Ceng LC, Wong NC: Viscosity approximation methods for equilibrium problems and fixed point problems of nonlinear semigroups. Taiwanese Journal of Mathematics 2009,13(5):1497–1513.
Martinez-Yanes C, Xu H-K: Strong convergence of the CQ method for fixed point iteration processes. Nonlinear Analysis: Theory, Methods & Applications 2006,64(11):2400–2411. 10.1016/j.na.2005.08.018
Xu HK: An iterative approach to quadratic optimization. Journal of Optimization Theory and Applications 2003,116(3):659–678. 10.1023/A:1023073621589
Shimizu T, Takahashi W: Strong convergence to common fixed points of families of nonexpansive mappings. Journal of Mathematical Analysis and Applications 1997,211(1):71–83. 10.1006/jmaa.1997.5398
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals. Journal of Mathematical Analysis and Applications 2005,305(1):227–239. 10.1016/j.jmaa.2004.11.017
Acknowledgment
This work was supported by the Vietnamese National Foundation of Science and Technology Development.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Buong, N., Duong, N. A Method for a Solution of Equilibrium Problem and Fixed Point Problem of a Nonexpansive Semigroup in Hilbert's Spaces. Fixed Point Theory Appl 2011, 208434 (2011). https://doi.org/10.1155/2011/208434
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/208434
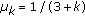 ,
,  ,
, 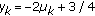 ,
,  for any fixed number
for any fixed number 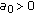 , and
, and 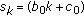 with
with 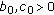 for all
for all 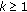 satisfy all conditions in Theorem 2.9.
satisfy all conditions in Theorem 2.9. for all
for all  and
and 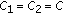 , then we have the following corollary.
, then we have the following corollary.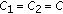 , a closed convex subset in
, a closed convex subset in 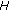 ,
,  for all
for all 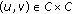 , we have the following result.
, we have the following result.