- Research Article
- Open access
- Published:
Convergence of Iterative Sequences for Common Zero Points of a Family of 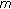 -Accretive Mappings in Banach Spaces
-Accretive Mappings in Banach Spaces
Fixed Point Theory and Applications volume 2011, Article number: 216173 (2011)
Abstract
We introduce implicit and explicit viscosity iterative algorithms for a finite family of  -accretive operators. Strong convergence theorems of the iterative algorithms are established in a reflexive Banach space which has a weakly continuous duality map.
-accretive operators. Strong convergence theorems of the iterative algorithms are established in a reflexive Banach space which has a weakly continuous duality map.
1. Introduction
Let  be a real Banach space, and let
be a real Banach space, and let  denote the normalized duality mapping from
denote the normalized duality mapping from  into
into  given by
given by

where  denotes the dual space of
denotes the dual space of  and
and  denotes the generalized duality pairing. In the sequel, we denote a single-valued normalized duality mapping by
denotes the generalized duality pairing. In the sequel, we denote a single-valued normalized duality mapping by  .
.
Let  be a nonempty subset of
be a nonempty subset of  . Recall that a mapping
. Recall that a mapping  is said to be a contraction if there exists a constant
is said to be a contraction if there exists a constant  such that
such that

Recall that a mapping  is said to be nonexpansive if
is said to be nonexpansive if

A point  is a fixed point of
is a fixed point of  provided
provided  . Denote by
. Denote by  the set of fixed points of
the set of fixed points of  , that is,
, that is,  . Given a real number
. Given a real number  and a contraction
and a contraction  , we define a mapping
, we define a mapping

It is obviously that  is a contraction on
is a contraction on  . In fact, for
. In fact, for  , we obtain
, we obtain

Let  be the unique fixed point of
be the unique fixed point of  , that is,
, that is,  is the unique solution of the fixed point equation
is the unique solution of the fixed point equation

A special case has been considered by Browder [1] in a Hilbert space as follows. Fix  and define a contraction
and define a contraction  on
on  by
by

We use  to denote the unique fixed point of
to denote the unique fixed point of  , which yields that
, which yields that  . In 1967, Browder [1] proved the following theorem.
. In 1967, Browder [1] proved the following theorem.
Theorem B.
In a Hilbert space, as  ,
,  converges strongly to a fixed point of
converges strongly to a fixed point of  , that is, closet to
, that is, closet to  , that is, the nearest point projection of
, that is, the nearest point projection of  onto
onto  .
.
In [2], Moudafi proposed a viscosity approximation method which was considered by many authors [2–8]. If  is a Hilbert space,
is a Hilbert space,  is a nonexpansive mapping and
is a nonexpansive mapping and  is a contraction, he proved the following theorems.
is a contraction, he proved the following theorems.
Theorem M1.
The sequence  generated by the following iterative scheme:
generated by the following iterative scheme:

converges strongly to the unique solution of the variational inequality

where  is a sequence of positive numbers tending to zero.
is a sequence of positive numbers tending to zero.
Theorem M2.
With and initial  defined the sequence
defined the sequence  by
by

Suppose that  , and
, and  and
and  . Then,
. Then,  converges strongly to the unique solution of the unique solutions of the variational inequality
converges strongly to the unique solution of the unique solutions of the variational inequality

Recall that a (possibly multivalued) operator  with domain
with domain  and range
and range  in
in  is accretive if for each
is accretive if for each  and
and 
 , there exists a
, there exists a  such that
such that

An accretive operator  is
is  -accretive if
-accretive if  for each
for each  . The set of zeros of
. The set of zeros of  is denoted by
is denoted by  . Hence,
. Hence,

For each  , we denote by
, we denote by  the resolvent of
the resolvent of  , that is,
, that is,  . Note that if
. Note that if  is
is  -accretive, then
-accretive, then  is nonexpansive and
is nonexpansive and  , for all
, for all  . We also denote by
. We also denote by  the Yosida approximation of
the Yosida approximation of  , that is,
, that is,  . It is known that
. It is known that  is a nonexpansive mapping from
is a nonexpansive mapping from  to
to  .
.
Recently, Kim and Xu [9] and Xu [10] studied the sequence generated by the following iterative algorithm:

where  is a real sequence
is a real sequence  and
and  . They obtained the strong convergence of the iterative algorithm in the framework of uniformly smooth Banach spaces and reflexive Banach space, respectively. Xu [10] also studied the following iterative algorithm by viscosity approximation method
. They obtained the strong convergence of the iterative algorithm in the framework of uniformly smooth Banach spaces and reflexive Banach space, respectively. Xu [10] also studied the following iterative algorithm by viscosity approximation method

where  is a real sequence
is a real sequence  ,
,  is a contractive mapping, and
is a contractive mapping, and  is a nonexpansive mapping with a fixed point. Strong convergence theorems of fixed points are obtained in a uniformly smooth Banach space; see [10] for more details.
is a nonexpansive mapping with a fixed point. Strong convergence theorems of fixed points are obtained in a uniformly smooth Banach space; see [10] for more details.
Very recently, Zegeye and Shahzad [11] studied the common zero problem of a family of  -accretive mappings. To be more precise, they proved the following result.
-accretive mappings. To be more precise, they proved the following result.
Theorem ZS.
Let  be a strictly convex and reflexive Banach space with a uniformly Gâteaux differentiable norm,
be a strictly convex and reflexive Banach space with a uniformly Gâteaux differentiable norm,  a nonempty, closed, convex subset of
a nonempty, closed, convex subset of  , and
, and 
 a family of
a family of  -accretive mappings with
-accretive mappings with  . For any
. For any  , let
, let  be generated by the algorithm
be generated by the algorithm

where  is a real sequence which satisfies the following conditions:
is a real sequence which satisfies the following conditions:  ;
;  ;
;  or
or  and
and  with
with  for
for  for
for  and
and  . If every nonempty, closed, bounded convex subset of
. If every nonempty, closed, bounded convex subset of  has the fixed point property for a nonexpansive mapping, then
has the fixed point property for a nonexpansive mapping, then  converges strongly to a common solution of the equations
converges strongly to a common solution of the equations  for
for  .
.
In this paper, motivated by the recent work announced in [3, 5, 9, 11–20], we consider the following implicit and explicit iterative algorithms by the viscosity approximation method for a finite family of  -accretive operators
-accretive operators  . The algorithms are as following:
. The algorithms are as following:


where  with
with  for
for  ,
,  and
and  is a real sequence in
is a real sequence in  . It is proved that the sequence
. It is proved that the sequence  generated in the iterative algorithms (1.17) and (1.18) converges strongly to a common zero point of a finite family of
generated in the iterative algorithms (1.17) and (1.18) converges strongly to a common zero point of a finite family of  -accretive mappings in reflexive Banach spaces, respectively.
-accretive mappings in reflexive Banach spaces, respectively.
2. Preliminaries
The norm of  is said to be Gâteaux differentiable (and
is said to be Gâteaux differentiable (and  is said to be smooth) if
is said to be smooth) if

exists for each  in its unit sphere
in its unit sphere  . It is said to be uniformly Fréchet differentiable (and
. It is said to be uniformly Fréchet differentiable (and  is said to be uniformly smooth) if the limit in (2.1) is attained uniformly for
is said to be uniformly smooth) if the limit in (2.1) is attained uniformly for  .
.
A Banach space  is said to be strictly convex if, for
is said to be strictly convex if, for  ,
,  , such that
, such that  ,
,

with  ,
,  , and
, and  for some
for some  . In a strictly convex Banach space
. In a strictly convex Banach space  , we have that, if
, we have that, if

for  ,
,  ,
,  , where
, where  , then
, then  (see [21]).
(see [21]).
Recall that a gauge is a continuous strictly increasing function  such that
such that  and
and  as
as  . Associated to a gauge
. Associated to a gauge  is the duality map
is the duality map  defined by
defined by

Following Browder [22], we say that a Banach space  has a weakly continuous duality map if there exists a gauge
has a weakly continuous duality map if there exists a gauge  for which the duality map
for which the duality map  is single valued and weak-to-weak* sequentially continuous (i.e., if
is single valued and weak-to-weak* sequentially continuous (i.e., if  is a sequence in
is a sequence in  weakly convergent to a point
weakly convergent to a point  , then the sequence
, then the sequence  converges weakly* to
converges weakly* to  ). It is known that
). It is known that  has a weakly continuous duality map for all
has a weakly continuous duality map for all  with the gauge
with the gauge  . In the case where
. In the case where  for all
for all  , we write the associated duality map as
, we write the associated duality map as  and call it the (normalized) duality map. Set
and call it the (normalized) duality map. Set

then

where  denotes the subdifferential in the sense of convex analysis. It also follows from (2.5) that
denotes the subdifferential in the sense of convex analysis. It also follows from (2.5) that  is convex and
is convex and  .
.
In order to prove our main results, we also need the following lemmas.
The first part of the next lemma is an immediate consequence of the subdifferential inequality, and the proof of the second part can be found in [23].
Lemma 2.1.
Assume that  has a weakly continuous duality map
has a weakly continuous duality map  with the gauge
with the gauge  .
.
(i)For all  and
and  , there holds the inequality
, there holds the inequality

In particular, for  and
and  ,
,

(ii)For  and for nonzero
and for nonzero  ,
,

Lemma 2.2 (see [24]).
Let  be a Banach space satisfying a weakly continuous duality map, let
be a Banach space satisfying a weakly continuous duality map, let  be a nonempty, closed, convex subset of
be a nonempty, closed, convex subset of  , and let
, and let  be a nonexpansive mapping with a fixed point. Then,
be a nonexpansive mapping with a fixed point. Then,  is demiclosed at zero, that is, if
is demiclosed at zero, that is, if  is a sequence in
is a sequence in  which converges weakly to
which converges weakly to  and if the sequence
and if the sequence  converges strongly to zero, then
converges strongly to zero, then  .
.
Lemma 2.3 (see [11]).
Let  be a nonempty, closed, convex subset of a strictly convex Banach space
be a nonempty, closed, convex subset of a strictly convex Banach space  . Let
. Let  ,
,  , be a family of
, be a family of  -accretive mappings such that
-accretive mappings such that  . Let
. Let  be real numbers in
be real numbers in  such that
such that  and
and  , where
, where  . Then,
. Then,  is nonexpansive and
is nonexpansive and  .
.
Lemma 2.4 (see [25]).
Let  be a sequence of nonnegative real numbers satisfying the condition
be a sequence of nonnegative real numbers satisfying the condition

where  and
and  such that
such that
(i) and
and  ,
,
(ii)either  or
or  .
.
Then  converges to zero.
converges to zero.
3. Main Results
Theorem 3.1.
Let  be a strictly convex and reflexive Banach space which has a weakly continuous duality map
be a strictly convex and reflexive Banach space which has a weakly continuous duality map  with the gauge
with the gauge  . Lek
. Lek  be a nonempty, closed, convex subset of
be a nonempty, closed, convex subset of  and
and  a contractive mapping with the coefficient
a contractive mapping with the coefficient  . Let
. Let  be a family of
be a family of  -accretive mappings with
-accretive mappings with  . Let
. Let  , for each
, for each  . For any
. For any  , let
, let  be generated by the algorithm (1.17), where
be generated by the algorithm (1.17), where  with
with  for
for  ,
,  and
and  is a sequence in
is a sequence in  . If
. If  , then
, then  converges strongly to a common solution
converges strongly to a common solution  of the equations
of the equations  for
for  , which solves the following variational inequality:
, which solves the following variational inequality:

Proof.
From Lemma 2.3, we see that  is a nonexpansive mapping and
is a nonexpansive mapping and

Notice that  is convex. From Lemma 2.1, for any fixed
is convex. From Lemma 2.1, for any fixed  , we have
, we have

which in turn implies that

Note that (3.4) actually holds for all duality maps  ; in particular, if we take the normalized duality
; in particular, if we take the normalized duality  (in which case, we have
(in which case, we have  ), then we get
), then we get

that is,

This implies that the sequence  is bounded. Now assume that
is bounded. Now assume that  is a weak limit point of
is a weak limit point of  and a subsequence
and a subsequence  of
of  converges weakly to
converges weakly to  . Then, by Lemma 2.2, we see that
. Then, by Lemma 2.2, we see that  is a fixed point of
is a fixed point of  . Hence,
. Hence,  . In (3.4), replacing
. In (3.4), replacing  with
with  and
and  with
with  , respectively, and taking the limit as
, respectively, and taking the limit as  , we obtain from the weak continuity of the duality map
, we obtain from the weak continuity of the duality map  that
that

Hence, we have  .
.
Next, we show that  solves the variation inequality (3.1). For
solves the variation inequality (3.1). For  , we obtain
, we obtain

which implies that

Replacing  with
with  in (3.9) and passing through the limit as
in (3.9) and passing through the limit as  , we conclude that
, we conclude that

It follows from Lemma 2.1 that  is a positive-scalar multiple of
is a positive-scalar multiple of  . We, therefore, obtain that
. We, therefore, obtain that  is a solution to (3.1).
is a solution to (3.1).
Finally, we prove that the full sequence  actually converges strongly to
actually converges strongly to  . It suffices to prove that the variational inequality (3.1) can have only one solution. This is an easy consequence of the contractivity of
. It suffices to prove that the variational inequality (3.1) can have only one solution. This is an easy consequence of the contractivity of  . Indeed, assume that both
. Indeed, assume that both  and
and  are solutions to (3.1). Then, we see that
are solutions to (3.1). Then, we see that

Adding them yields that

This implies that

which guarantees  . So, (3.1) can have at most one solution. This completes the proof.
. So, (3.1) can have at most one solution. This completes the proof.
Next, we shall consider the explicit algorithm (1.18) which is rephrased below, the initial guess  is arbitrary and
is arbitrary and

We need the strong convergence of the implicit algorithm (1.17) to prove the strong convergence of the explicit algorithm (3.14).
Theorem 3.2.
Let  be a strictly convex and reflexive Banach space which has a weakly continuous duality map
be a strictly convex and reflexive Banach space which has a weakly continuous duality map  with the gauge
with the gauge  . Lek
. Lek  be a nonempty, closed, convex subset of
be a nonempty, closed, convex subset of  and
and  a contractive mapping. Let
a contractive mapping. Let  be a family of
be a family of  -accretive mappings with
-accretive mappings with  . Let
. Let  for each
for each  . For any
. For any  , let
, let  be generated by the algorithm (1.18), where
be generated by the algorithm (1.18), where  with
with  for
for  ,
,  , and
, and  is a sequence in
is a sequence in  which satisfies the following conditions:
which satisfies the following conditions:  and
and  . Assume also that
. Assume also that
(i) ,
,
(ii) converges strongly to
converges strongly to  , where
, where  is the sequence generated by the implicity algorithm (1.17).
is the sequence generated by the implicity algorithm (1.17).
Then,  converges strongly to
converges strongly to  , which solves the variational inequality (3.1).
, which solves the variational inequality (3.1).
Proof.
From Lemma 2.3, we obtain that  is a nonexpansive mapping and
is a nonexpansive mapping and

We observe that  is bounded. Indeed, take
is bounded. Indeed, take  and notice that
and notice that

By simple inductions, we have

which gives that the sequence  is bounded, so are
is bounded, so are  and
and  . From (1.17), we have
. From (1.17), we have

This implies that

which in turn implies that

It follows from  that
that

From the assumption  and the weak continuity of
and the weak continuity of  imply that,
imply that,

Letting  in (3.21), we obtain that
in (3.21), we obtain that

Finally, we show the sequence  converges stongly to
converges stongly to  . Observe that
. Observe that

It follows from Lemma 2.1 that

which yields that

where  is a appropriate constant such that
is a appropriate constant such that  . In view of Lemma 2.4, we can obtain the desired conclusion easily. This completes the proof.
. In view of Lemma 2.4, we can obtain the desired conclusion easily. This completes the proof.
As an application of Theorems 3.1 and 3.2, we have the following results for a single mapping.
Corollary 3.3.
Let  be a reflexive Banach space which has a weakly continuous duality map
be a reflexive Banach space which has a weakly continuous duality map  with the gauge
with the gauge  . Lek
. Lek  be a nonempty, closed, convex subset of
be a nonempty, closed, convex subset of  and
and  a contractive mapping with the coefficient
a contractive mapping with the coefficient  . Let
. Let  be a
be a  -accretive mapping with
-accretive mapping with  . Let
. Let  . For any
. For any  , let
, let  be generated by the following iterative algorithm:
be generated by the following iterative algorithm:

Then,  converges strongly to a solution of the equations
converges strongly to a solution of the equations  .
.
Corollary 3.4.
Let  be a reflexive Banach space which has a weakly continuous duality map
be a reflexive Banach space which has a weakly continuous duality map  with gauge
with gauge  . Let
. Let  be a nonempty, closed, convex subset of
be a nonempty, closed, convex subset of  and
and  a contractive mapping. Let
a contractive mapping. Let  be a
be a  -accretive mappings with
-accretive mappings with  . Let
. Let  . For any
. For any  , let
, let  be generated by the following algorithm:
be generated by the following algorithm:

where  is a sequence in
is a sequence in  which satisfies the following conditions:
which satisfies the following conditions:  and
and  . Also assume that
. Also assume that
(i) ,
,
(ii) converges strongly to
converges strongly to  , where
, where  is the sequence generated by the implicity scheme (3.27) and
is the sequence generated by the implicity scheme (3.27) and  .
.
Then, the sequence  generated by the following iterative algorithm
generated by the following iterative algorithm

converges strongly to a solution  of the equation
of the equation  .
.
References
Browder FE: Convergence of approximants to fixed points of nonexpansive non-linear mappings in Banach spaces. Archive for Rational Mechanics and Analysis 1967, 24: 82–90.
Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000,241(1):46–55. 10.1006/jmaa.1999.6615
Cho YJ, Qin X: Viscosity approximation methods for a family of -accretive mappings in reflexive Banach spaces. Positivity 2008,12(3):483–494. 10.1007/s11117-007-2181-8
Cho YJ, Kang SM, Qin X: Some results on -strictly pseudo-contractive mappings in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,70(5):1956–1964. 10.1016/j.na.2008.02.094
Cho YJ, Kang SM, Qin X: Approximation of common fixed points of an infinite family of nonexpansive mappings in Banach spaces. Computers & Mathematics with Applications 2008,56(8):2058–2064. 10.1016/j.camwa.2008.03.035
Ceng L-C, Xu H-K, Yao J-C: The viscosity approximation method for asymptotically nonexpansive mappings in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,69(4):1402–1412. 10.1016/j.na.2007.06.040
Qin X, Cho YJ, Kang SM: Viscosity approximation methods for generalized equilibrium problems and fixed point problems with applications. Nonlinear Analysis: Theory, Methods & Applications 2010,72(1):99–112. 10.1016/j.na.2009.06.042
Xu H-K: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004,298(1):279–291. 10.1016/j.jmaa.2004.04.059
Kim T-H, Xu H-K: Strong convergence of modified Mann iterations. Nonlinear Analysis: Theory, Methods & Applications 2005,61(1–2):51–60. 10.1016/j.na.2004.11.011
Xu H-K: Strong convergence of an iterative method for nonexpansive and accretive operators. Journal of Mathematical Analysis and Applications 2006,314(2):631–643. 10.1016/j.jmaa.2005.04.082
Zegeye H, Shahzad N: Strong convergence theorems for a common zero for a finite family of -accretive mappings. Nonlinear Analysis: Theory, Methods & Applications 2007,66(5):1161–1169. 10.1016/j.na.2006.01.012
Agarwal RP, Zhou H, Cho YJ, Kang SM: Zeros and mapping theorems for perturbations of -accretive operators in Banach spaces. Computers & Mathematics with Applications 2005,49(1):147–155. 10.1016/j.camwa.2005.01.012
Dominguez Benavides T, Lopez Acedo G, Xu H-K: Iterative solutions for zeros of accretive operators. Mathematische Nachrichten 2003, 248/249: 62–71. 10.1002/mana.200310003
Kirk WA: On successive approximations for nonexpansive mappings in Banach spaces. Glasgow Mathematical Journal 1971, 12: 6–9. 10.1017/S0017089500001063
Liu G, Lei D, Li S: Approximating fixed points of nonexpansive mappings. International Journal of Mathematics and Mathematical Sciences 2000,24(3):173–177. 10.1155/S0161171200003252
Maiti M, Saha B: Approximating fixed points of nonexpansive and generalized nonexpansive mappings. International Journal of Mathematics and Mathematical Sciences 1993,16(1):81–86. 10.1155/S0161171293000092
Park S: Fixed point theorems in locally -convex spaces. Nonlinear Analysis: Theory, Methods & Applications 2002,48(6):869–879. 10.1016/S0362-546X(00)00220-0
Park S: Fixed point theory of multimaps in abstract convex uniform spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(7–8):2468–2480. 10.1016/j.na.2009.01.081
Qin X, Su Y: Approximation of a zero point of accretive operator in Banach spaces. Journal of Mathematical Analysis and Applications 2007,329(1):415–424. 10.1016/j.jmaa.2006.06.067
Yao Y, Liou Y-C: Strong convergence to common fixed points of a finite family of asymptotically nonexpansive map. Taiwanese Journal of Mathematics 2007,11(3):849–865.
Takahashi W: Nonlinear Functional Analysis, Fixed Point theory and Its Applications. Yokohama Publishers, Yokohama, Japan; 2000:iv+276.
Browder FE: Convergence theorems for sequences of nonlinear operators in Banach spaces. Mathematische Zeitschrift 1967, 100: 201–225. 10.1007/BF01109805
Xu ZB, Roach GF: Characteristic inequalities of uniformly convex and uniformly smooth Banach spaces. Journal of Mathematical Analysis and Applications 1991,157(1):189–210. 10.1016/0022-247X(91)90144-O
Lim T-C, Xu HK: Fixed point theorems for asymptotically nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 1994,22(11):1345–1355. 10.1016/0362-546X(94)90116-3
Xu H-K: Iterative algorithms for nonlinear operators. Journal of the London Mathematical Society 2002,66(1):240–256. 10.1112/S0024610702003332
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Qing, Y., Cho, S. & Qin, X. Convergence of Iterative Sequences for Common Zero Points of a Family of 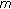 -Accretive Mappings in Banach Spaces.
Fixed Point Theory Appl 2011, 216173 (2011). https://doi.org/10.1155/2011/216173
-Accretive Mappings in Banach Spaces.
Fixed Point Theory Appl 2011, 216173 (2011). https://doi.org/10.1155/2011/216173
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/216173