- Research Article
- Open access
- Published:
Approximation of Common Solutions to System of Mixed Equilibrium Problems, Variational Inequality Problem, and Strict Pseudo-Contractive Mappings
Fixed Point Theory and Applications volume 2011, Article number: 347204 (2011)
Abstract
We introduce an iterative algorithm for finding a common element of the set of fixed points of strict pseudocontractions mapping, the set of common solutions of a system of two mixed equilibrium problems and the set of common solutions of the variational inequalities with inverse strongly monotone mappings. Strong convergence theorems are established in the framework of Hilbert spaces. Finally, we apply our results for solving convex feasibility problems in Hilbert spaces. Our results improve and extend the corresponding results announced by many others recently.
1. Introduction
Throughout this paper, we denote by  and
and  the sets of positive integers and real numbers, respectively. Let
the sets of positive integers and real numbers, respectively. Let  be a real Hilbert space with inner product
be a real Hilbert space with inner product  and norm
and norm  , and let
, and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . We denote weak convergence and strong convergence by notations
. We denote weak convergence and strong convergence by notations  and
and  , respectively. Recall that a mapping
, respectively. Recall that a mapping  is an
is an  -contraction on
-contraction on  if there exists a constant
if there exists a constant  such that
such that  for all
for all  . Let
. Let  be a mapping. In the sequel, we will use
be a mapping. In the sequel, we will use  to denote the set of fixed points of
to denote the set of fixed points of  ; that is,
; that is,  . In addition, let a mapping
. In addition, let a mapping  be callednonexpansive, if
be callednonexpansive, if  , for all
, for all  . It is well known that if
. It is well known that if  is nonempty, bounded, closed, and convex and
is nonempty, bounded, closed, and convex and  is a nonexpansive self-mapping on
is a nonexpansive self-mapping on  , then
, then  is nonempty; see, for example, [1]. Recall that a mapping
is nonempty; see, for example, [1]. Recall that a mapping  is called strictly pseudo-contraction if there exists a constant
is called strictly pseudo-contraction if there exists a constant  such that
such that

where  denotes the identity operator on
denotes the identity operator on  . Note that if
. Note that if  , then
, then  is a nonexpansive mapping. The class of strict pseudo-contractions is one of the most important classes of mappings among nonlinear mappings. Within the past several decades, many authors have been devoted to the studies on the existence and convergence of fixed points for strict pseudo-contractions. In 1967, Browder and Petryshyn [2] introduced a convex combination method to study strict pseudo-contractions in Hilbert spaces. On the other hand, Marino and Xu [3] and Zhou [4] developed some iterative scheme for finding a fixed point of a strict pseudo-contraction mapping. More precisely, take
is a nonexpansive mapping. The class of strict pseudo-contractions is one of the most important classes of mappings among nonlinear mappings. Within the past several decades, many authors have been devoted to the studies on the existence and convergence of fixed points for strict pseudo-contractions. In 1967, Browder and Petryshyn [2] introduced a convex combination method to study strict pseudo-contractions in Hilbert spaces. On the other hand, Marino and Xu [3] and Zhou [4] developed some iterative scheme for finding a fixed point of a strict pseudo-contraction mapping. More precisely, take  and define a mapping
and define a mapping  by
by

where  is a strict pseudo-contraction. Under appropriate restrictions on
is a strict pseudo-contraction. Under appropriate restrictions on  , it is proved that the mapping
, it is proved that the mapping  is nonexpansive. Therefore, the techniques of studying nonexpansive mappings can be applied to study more general strict pseudo-contractions.
is nonexpansive. Therefore, the techniques of studying nonexpansive mappings can be applied to study more general strict pseudo-contractions.
Let  be a proper extended real-valued function and let
be a proper extended real-valued function and let  be a bifunction of
be a bifunction of  into
into  such that
such that  , where
, where  is the set of real numbers and
is the set of real numbers and  . Ceng and Yao [5] considered the following mixed equilibrium problems for finding
. Ceng and Yao [5] considered the following mixed equilibrium problems for finding  such that
such that

The set of solutions of (1.3) is denoted by  , that is,
, that is,

We see that  is a solution of a problem (1.3) that implies that
is a solution of a problem (1.3) that implies that  .
.
Special Examples
-
(1)
If
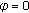 , then the mixed equilibrium problem (1.3) becomes to be the equilibrium problem which is to find
, then the mixed equilibrium problem (1.3) becomes to be the equilibrium problem which is to find  such that
such that 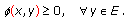 (1.5)
(1.5)
The set of solutions of (1.5) is denoted by  .
.
-
(2)
If
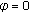 and
and 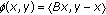 for all
for all 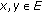 , where
, where  is a nonlinear mapping, then problem (1.5) becomes to be the variational inequality problems which is to find
is a nonlinear mapping, then problem (1.5) becomes to be the variational inequality problems which is to find 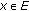 such that
such that  (1.6)
(1.6)
The set of solutions of (1.6) is denoted by  . The variational inequality has been extensively studied in the literature. See, for example, [6–8] and the references therein.
. The variational inequality has been extensively studied in the literature. See, for example, [6–8] and the references therein.
The mixed equilibrium problems include fixed point problems, variational inequality problems, optimization problems, Nash equilibrium problems, and the equilibrium problem as special cases. Numerous problems in physics, optimization, and economics reduce to find a solution of (1.3). Some authors have proposed some useful methods for solving the  and
and  ; see, for instance [5, 9–27]. In 1997, Combettes and Hirstoaga [10] introduced an iterative scheme of finding the best approximation to initial data when
; see, for instance [5, 9–27]. In 1997, Combettes and Hirstoaga [10] introduced an iterative scheme of finding the best approximation to initial data when  is nonempty and proved a strong convergence theorem. Next, we recall some definitions.
is nonempty and proved a strong convergence theorem. Next, we recall some definitions.
Definition 1.1.
Let  be nonlinear mappings. Then
be nonlinear mappings. Then  is called
is called
(1)monotone if

(2) -strongly monotone if there exists a constant
-strongly monotone if there exists a constant  such that
such that

(3) -Lipschitz continuous if there exists a constant
-Lipschitz continuous if there exists a constant  such that
such that

(4) -inverse strongly monotone if there exists a constant
-inverse strongly monotone if there exists a constant  such that
such that

Remark 1.2.
It is obvious that any  -inverse strongly monotone mappings
-inverse strongly monotone mappings  is monotone and
is monotone and  -Lipschitz continuous.
-Lipschitz continuous.
-
(5)
A set-valued mapping
 is called amonotone if, for all
is called amonotone if, for all  ,
, 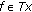 and
and 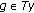 imply
imply  .
. -
(6)
A monotone mapping
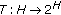 is a maximal if the graph of
is a maximal if the graph of 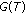 of
of 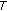 is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping
is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping  is maximal if and only if for
is maximal if and only if for  ,
, 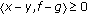 for every
for every  implies
implies  .
.
Let  be a monotone map of
be a monotone map of  into
into  ,
,  -Lipschitz continuous mapping and let
-Lipschitz continuous mapping and let  be the normal cone to
be the normal cone to  when
when  , that is,
, that is,

and define a mapping  on
on  by
by

Then  is the maximal monotone and
is the maximal monotone and  if and only if
if and only if  ; see [28].
; see [28].
For finding a common element of the set of fixed points of a nonexpansive mapping and the set of solution of variational inequalities for  -inverse strongly monotone, Takahashi and Toyoda [29] first introduced the following iterative scheme:
-inverse strongly monotone, Takahashi and Toyoda [29] first introduced the following iterative scheme:

where  is an
is an  -inverse strongly monotone,
-inverse strongly monotone,  is a sequence in (0, 1), and
is a sequence in (0, 1), and  is a sequence in
is a sequence in  . They showed that if
. They showed that if  is nonempty, then the sequence
is nonempty, then the sequence  generated by (1.13) converges weakly to some
generated by (1.13) converges weakly to some  .
.
Further, Y. Yao and J.-C. Yao [30] introduced the following iterative scheme:

where  is an
is an  -inverse strongly monotone,
-inverse strongly monotone,  ,
,  ,
,  are three sequences in [0, 1], and
are three sequences in [0, 1], and  is a sequence in
is a sequence in  . They showed that if
. They showed that if  is nonempty, then the sequence
is nonempty, then the sequence  generated by (1.14) converges strongly to some
generated by (1.14) converges strongly to some  .
.
A map  is said to be strongly positive if there exists a constant
is said to be strongly positive if there exists a constant  such that
such that

A typical problem is to minimize a quadratic function over the set of the fixed points of some nonexpansive mapping on a real Hilbert space  :
:

where  is some linear,
is some linear,  is the fixed point set of a nonexpansive mapping
is the fixed point set of a nonexpansive mapping  on
on  and
and  is a point in
is a point in  . Let
. Let  be a strongly positive linear bounded map on
be a strongly positive linear bounded map on  with coefficient
with coefficient  . In 2006, Marino and Xu [31] studied the following general iterative method:
. In 2006, Marino and Xu [31] studied the following general iterative method:

They proved that if the sequence  of parameters appropriate conditions, then the sequence
of parameters appropriate conditions, then the sequence  generated by (1.17) converges strongly to
generated by (1.17) converges strongly to  . Recently, Plubtieng and Punpaeng [32] proposed the following iterative algorithm:
. Recently, Plubtieng and Punpaeng [32] proposed the following iterative algorithm:

They proved that if the sequences  and
and  of parameters satisfy appropriate condition, then both sequences
of parameters satisfy appropriate condition, then both sequences  and
and  converge to the unique solution
converge to the unique solution  of the variational inequality
of the variational inequality

which is the optimality condition for the minimization problem

where  is a potential function for
is a potential function for  (i.e.,
(i.e.,  for
for  ).
).
On the other hand, for finding a common element of the set of fixed points of a  -strict pseudo-contraction mapping and the set of solutions of an equilibrium problem in a real Hilbert space, Liu [33] introduced the following iterative scheme:
-strict pseudo-contraction mapping and the set of solutions of an equilibrium problem in a real Hilbert space, Liu [33] introduced the following iterative scheme:

where  is a
is a  -strict pseudo-contraction mapping and
-strict pseudo-contraction mapping and  ,
,  are sequences in [0, 1]. They proved that under certain appropriate conditions over
are sequences in [0, 1]. They proved that under certain appropriate conditions over  ,
,  , and
, and  , the sequences
, the sequences  and
and  converge strongly to some
converge strongly to some  , which solves some variational inequality problems.
, which solves some variational inequality problems.
In 2008, Ceng and Yao [5] introduced an iterative scheme for finding a common fixed point of a finite family of nonexpansive mappings and the set of solutions of a problem (1.3) in Hilbert spaces and obtained the strong convergence theorem which used the following condition:
-
(H)
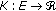 is
is 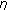 -strongly convex with constant
-strongly convex with constant 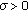 and its derivative
and its derivative 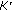 is sequentially continuous from weak topology to strong topology. We note that the condition (H) for the function
is sequentially continuous from weak topology to strong topology. We note that the condition (H) for the function 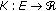 is a very strong condition. We also note that the condition (H) does not cover the case
is a very strong condition. We also note that the condition (H) does not cover the case  and
and 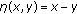 for each
for each 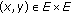 . Very recently, R. Wangkeeree and R. Wangkeeree [34] introduced a general iterative method for finding a common element of the set of solutions of the mixed equilibrium problems, the set of fixed point of a
. Very recently, R. Wangkeeree and R. Wangkeeree [34] introduced a general iterative method for finding a common element of the set of solutions of the mixed equilibrium problems, the set of fixed point of a 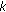 -strict pseudo-contraction mapping, and the set of solutions of the variational inequality for an inverse strongly monotone mapping in Hilbert spaces. They obtained a strong convergence theorem except the condition (H) for the sequences generated by these processes.
-strict pseudo-contraction mapping, and the set of solutions of the variational inequality for an inverse strongly monotone mapping in Hilbert spaces. They obtained a strong convergence theorem except the condition (H) for the sequences generated by these processes.
In 2009, Qin et al. [35] introduced a general iterative scheme for finding a common element of the set of common solution of generalized equilibrium problems, the set of a common fixed point of a family of infinite nonexpansive mappings in Hilbert spaces. Let  be the sequence generated iterative by the following algorithm:
be the sequence generated iterative by the following algorithm:

They proved that under certain appropriate conditions imposed on  ,
,  ,
,  and
and  , the sequence
, the sequence  generated by (1.22) converges strongly to
generated by (1.22) converges strongly to  , where
, where  .
.
In the present paper, motivated and inspired by Qin et al. [35], Plubtieng and Punpaeng [32], Peng and Yao [17], R. Wangkeeree and R. Wangkeeree [34], and Y. Yao and J.-C. Yao [30], we introduce a new approximation iterative scheme for finding a common element of the set of fixed points of strict pseudo-contractions, the set of common solutions of the system of a mixed equilibrium problem, and the set of common solutions of the variational inequalities with inverse strongly monotone mappings in Hilbert spaces. We obtain a strong convergence theorem for the sequences generated by these processes under some parameter controlling conditions. Moreover, we apply our results for solving convex feasibility problems in Hilbert spaces. The results in this paper extend and improve some well-known results in [17, 30, 32, 34, 35].
2. Preliminaries
Let  be a real Hilbert space and
be a real Hilbert space and  be a closed convex subset of
be a closed convex subset of  . In a real Hilbert space
. In a real Hilbert space  , it is well known that
, it is well known that

for all  and
and  .
.
For any  , there exists a unique nearest point in
, there exists a unique nearest point in  , denoted by
, denoted by  , such that
, such that

The mapping  is called the metric projection of
is called the metric projection of  onto
onto  .
.
It is well known that  is a firmly nonexpansive mapping of
is a firmly nonexpansive mapping of  onto
onto  , that is,
, that is,

Further, for any  and
and  ,
,  if and only if
if and only if  , for all
, for all  .
.
Moreover,  is characterized by the following properties:
is characterized by the following properties:  and
and


for all  .
.
It is easy to see that the following is true:

The following lemmas will be useful for proving the convergence result of this paper.
Lemma 2.1 (see [36]).
Let  be an inner product space. Then, for all
be an inner product space. Then, for all  and
and  with
with  , one has
, one has

Lemma 2.2 (see [31]).
Assume that  is a strongly positive linear bounded operator on
is a strongly positive linear bounded operator on  with coefficient
with coefficient  and
and  . Then
. Then  .
.
Lemma 2.3 (see [4]).
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  and let
and let  be a
be a  -strict pseudo-contraction with a fixed point. Then
-strict pseudo-contraction with a fixed point. Then  is closed and convex. Define
is closed and convex. Define  by
by  for each
for each  . Then
. Then  is nonexpansive such that
is nonexpansive such that  .
.
Lemma 2.4 (see [37]).
Let  be a uniformly convex Banach spaces,
be a uniformly convex Banach spaces,  be a nonempty closed convex subset of
be a nonempty closed convex subset of  and
and  be a nonexpansive mapping. Then
be a nonexpansive mapping. Then  is demi-closed at zero.
is demi-closed at zero.
Lemma 2.5 (see [38]).
Let  be a nonempty closed convex subset of strictly convex Banach space
be a nonempty closed convex subset of strictly convex Banach space  . Let
. Let  be a sequence of nonexpansive mappings on
be a sequence of nonexpansive mappings on  . Suppose
. Suppose  is nonempty. Let
is nonempty. Let  be a sequence of positive numbers with
be a sequence of positive numbers with  . Then a mapping
. Then a mapping  on
on  can be defined by
can be defined by

for  is well defined, nonexpansive and
is well defined, nonexpansive and  holds.
holds.
In order to solve the mixed equilibrium problem, the following assumptions are given for the bifunction  ,
,  and the set
and the set  :
:
(A1) for all
for all  ;
;
(A2) is monotone, that is,
is monotone, that is,  for all
for all  ;
;
(A3) for each  ,
,  ;
;
(A4) for each  is convex and lower semicontinuous;
is convex and lower semicontinuous;
(A5) for each  is weakly upper semicontinuous;
is weakly upper semicontinuous;
(B1) for each  and
and  , there exist abounded subset
, there exist abounded subset  and
and  such that for any
such that for any  ,
,

(B2) is a bounded set.
is a bounded set.
Lemma 2.6 (see [39]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a bifunction satisfies (A1)–(A5) and let
be a bifunction satisfies (A1)–(A5) and let  be a proper lower semicontinuous and convex function. Assume that either (B1) or (B2) holds. For
be a proper lower semicontinuous and convex function. Assume that either (B1) or (B2) holds. For  and
and  , define a mapping
, define a mapping  as follows:
as follows:

for all  . Then, the following holds:
. Then, the following holds:
(i)for each  ,
,  ;
;
(ii) is single-valued;
is single-valued;
(iii) is firmly nonexpansive, that is, for any
is firmly nonexpansive, that is, for any  ,
,

(iv) ;
;
(v) is closed and convex.
is closed and convex.
Remark 2.7.
If  , then
, then  is rewritten as
is rewritten as  .
.
Remark 2.8.
We remark that Lemma 2.6 is not a consequence of Lemma 3.1 in [5], because the condition of the sequential continuity from the weak topology to the strong topology for the derivative  of the function
of the function  does not cover the case
does not cover the case  .
.
Lemma 2.9 (see [40]).
Let  and
and  be bounded sequences in a Banach space
be bounded sequences in a Banach space  and let
and let  be a sequence in
be a sequence in  with
with  . Suppose
. Suppose  for all integers
for all integers  and
and  . Then,
. Then,  .
.
Lemma 2.10 (see [41]).
Assume that  is a sequence of nonnegative real numbers such that
is a sequence of nonnegative real numbers such that

where  is a sequence in
is a sequence in  and
and  is a sequence in
is a sequence in  such that
such that
(1) ,
,
(2) or
or  .
.
Then  .
.
Lemma 2.11.
Let  be a real Hilbert space. Then for all
be a real Hilbert space. Then for all  ,
,

3. Main Results
In this section, we will use the new approximation iterative method to prove a strong convergence theorem for finding a common element of the set of fixed points of strict pseudo-contractions, the set of common solutions of the system of a mixed equilibrium problem and the set of a common solutions of the variational inequalities with inverse strongly monotone mappings in a real Hilbert space.
Theorem 3.1.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  and
and  be two bifunctions from
be two bifunctions from  to
to  satisfying (A1)–(A5) and let
satisfying (A1)–(A5) and let  be a proper lower semicontinuous and convex function. Let
be a proper lower semicontinuous and convex function. Let  be an
be an  -inverse strongly monotone mapping and
-inverse strongly monotone mapping and  be an
be an  -inverse strongly monotone mapping. Let
-inverse strongly monotone mapping. Let  be a contraction mapping with coefficient
be a contraction mapping with coefficient  and let
and let  be a strongly positive linear bounded operator on
be a strongly positive linear bounded operator on  with coefficient
with coefficient  and
and  . Let
. Let  be a
be a  -strict pseudo-contraction with a fixed point. Define a mapping
-strict pseudo-contraction with a fixed point. Define a mapping  by
by  , for all
, for all  . Assume that
. Assume that

Assume that either (B1) or (B2). Let  be a sequence generated by the following iterative algorithm:
be a sequence generated by the following iterative algorithm:

where  ,
,  ,
,  ,
,  , and
, and  are sequences in
are sequences in  and
and  ,
,  are positive sequences. Assume that the control sequences satisfy the following restrictions:
are positive sequences. Assume that the control sequences satisfy the following restrictions:
(C1) ,
,
(C2) and
and  ,
,
(C3) ,
,
(C4) ,
,
(C5) ,
,  , where
, where  are two positive constants,
are two positive constants,
(C6) ,
,  and
and  , for some
, for some  .
.
Then,  converges strongly to a point
converges strongly to a point  which is the unique solution of the variational inequality
which is the unique solution of the variational inequality

or equivalent  , where
, where  is a metric projection mapping form
is a metric projection mapping form  onto
onto  .
.
Proof.
Since  , as
, as  , we may assume, without loss of generality, that
, we may assume, without loss of generality, that  for all
for all  . By Lemma 2.2, we know that if
. By Lemma 2.2, we know that if  , then
, then  . We will assume that
. We will assume that  . Since
. Since  is a strongly positive bounded linear operator on
is a strongly positive bounded linear operator on  , we have
, we have

Observe that

so this shows that  is positive. It follows that
is positive. It follows that

We divide the proof into seven steps.
Step 1.
We claim that the mapping  where
where  has a unique fixed point.
has a unique fixed point.
Since  be a contraction of
be a contraction of  into itself with
into itself with  . Then, we have
. Then, we have

Since  , it follows that
, it follows that  is a contraction of
is a contraction of  into itself. Therefore the Banach Contraction Mapping Principle implies that there exists a unique element
into itself. Therefore the Banach Contraction Mapping Principle implies that there exists a unique element  such that
such that  .
.
Step 2.
We claim that  is nonexpansive.
is nonexpansive.
Indeed, from the  -inverse strongly monotone mapping definition on
-inverse strongly monotone mapping definition on  and condition (C5), we have
and condition (C5), we have

where  , for all
, for all  implies that the mapping
implies that the mapping  is nonexpansive and so is,
is nonexpansive and so is,  .
.
Step 3.
We claim that  is bounded.
is bounded.
Indeed, let  and Lemma 2.6, we obtain
and Lemma 2.6, we obtain

Note that  and
and  , we have
, we have

Since  and
and  are nonexpansive and from (2.6), we have
are nonexpansive and from (2.6), we have

From Lemma 2.3, we have that  is nonexpansive with
is nonexpansive with  . It follows that
. It follows that

It follows that

By simple induction, we have

Hence,  is bounded, so are
is bounded, so are  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  .
.
Step 4.
We claim that  .
.
Observing that  and
and  , by the nonexpansiveness of
, by the nonexpansiveness of  , we get
, we get

Similarly, let  and
and  , we have
, we have

From  and
and  , we compute
, we compute

Similarly, we have

Observing that

we obtain

Substituting (3.17) and (3.18) into (3.20), we have

where  is an appropriate constant such that
is an appropriate constant such that  ,
, ,
, ,
,  ,
, .
.
Putting  , for all
, for all  , we have
, we have

Then, we compute

It follows from (3.21) and (3.23), that

This together with (C2), (C3), (C4), and (C6) imply that

Hence, by Lemma 2.9, we obtain  as
as  . It follows that
. It follows that

So, we also get

Observe that

By condition (C2) and (3.26), we have

Step 5.
We claim that the following statements hold:
(s1) ;
;
(s2) ;
;
(s3) ;
;
(s4) .
.
Indeed, pick any  , to obtain
, to obtain

Therefore,

Similarly, we have

Note that

Substituting (3.31) and (3.32) into (3.33), we obtain

From Lemma 2.1, (3.2) and (3.34), we obtain

It follows that

From (C2), (C6), and (3.26), we also have

Similarly, using (3.35) again, we have

From (C2), (C6), and (3.26), we also have

From (3.37) and (3.39), we have

For  , we compute
, we compute

Similarly, we have

Substituting (3.41) and (3.42) into (3.33), we also have

On the other hand, we note that

It follows that

From (C2), (C5), (C6), and (3.26), we have

Thanks to (3.44), we also have

From (C2), (C5), (C6), and (3.26), we obtain

Observe that

and hence

Similarly, we can obtain that

Substituting (3.50) and (3.51) into (3.33), we also have

On the other hand, we have

and hence

From (C2), (C6), (3.26), (3.46), and (3.48), we also have

Similarly, using (3.53) again, we can prove

From (3.39) and (3.55), we also have

From (3.37) and (3.56), we have

Step 6.
We claim that  , where
, where  is the unique solution of the variational inequality
is the unique solution of the variational inequality  , for all
, for all  .
.
To show this inequality, we choose a subsequence  of
of  such that
such that

Since  is bounded, there exists a subsequence
is bounded, there exists a subsequence  of
of  which converges weakly to
which converges weakly to  . Without loss of generality, we can assume that
. Without loss of generality, we can assume that  . We claim that
. We claim that  .
.
(a1) First, we prove that  .
.
Assume also that  and
and  .
.
Define a mapping  by
by

where  ,
,  , and
, and  , for some
, for some  . From Lemma 2.5, we have that
. From Lemma 2.5, we have that  is nonexpansive with
is nonexpansive with

Notice that

where  is an appropriate constant such that
is an appropriate constant such that

From (C6), (3.37), (3.39), and (3.29), we obtain

By Lemma 2.4, we have  , that is,
, that is,  .
.
(a2) Now, we prove that  .
.
Define a mapping  by
by

where  ,
,  , and
, and  , for some
, for some  . From Lemma 2.5, we have that
. From Lemma 2.5, we have that  is nonexpansive with
is nonexpansive with

On the other hand, we have

where  is an appropriate constant such that
is an appropriate constant such that

From (C6) and (3.29), we obtain

Since  is a contraction with the coefficient
is a contraction with the coefficient  , there exists a unique fixed point. We use
, there exists a unique fixed point. We use  to denote the unique fixed point to the mapping
to denote the unique fixed point to the mapping  , that is,
, that is,  . Since
. Since  is bounded, There exists a subsequence
is bounded, There exists a subsequence  of
of  which converges weakly to
which converges weakly to  . Without loss of generality, we may assume that
. Without loss of generality, we may assume that  . It follows from (3.69), that
. It follows from (3.69), that

It follows from Lemma 2.4, we obtain that  . Hence
. Hence  , where
, where  . From (3.59) and (2.4), we arrive at
. From (3.59) and (2.4), we arrive at

On the other hand, we have

From (3.26) and (3.71), we obtain that

Step 7.
We claim that  .
.
Indeed, by (3.2) and using Lemmas 2.2 and 2.11, we observe that

which implies that

Taking

Then we can rewrite (3.75) as

We have  . Applying Lemma 2.10 to (3.77), we conclude that
. Applying Lemma 2.10 to (3.77), we conclude that  converges strongly to
converges strongly to  in norm. This completes the proof.
in norm. This completes the proof.
If the mapping  is nonexpansive, then
is nonexpansive, then  . We can obtain the following result from Theorem 3.1 immediately.
. We can obtain the following result from Theorem 3.1 immediately.
Corollary 3.2.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let
. Let  and
and  be two bifunction from
be two bifunction from  to
to  satisfying (A1)–(A4) and let
satisfying (A1)–(A4) and let  be a proper lower semicontinuous and convex function. Let
be a proper lower semicontinuous and convex function. Let  be an
be an  -inverse strongly monotone mapping and
-inverse strongly monotone mapping and  be an
be an  -inverse strongly monotone mapping. Let
-inverse strongly monotone mapping. Let  be a contraction mapping with coefficient
be a contraction mapping with coefficient  and let
and let  be a strongly positive linear bounded operator on
be a strongly positive linear bounded operator on  with coefficient
with coefficient  and
and  . Let
. Let  a nonexpansive mapping with a fixed point. Assume that
a nonexpansive mapping with a fixed point. Assume that

Assume that either  or
or  . Let
. Let  be a sequence generated by the following iterative algorithm:
be a sequence generated by the following iterative algorithm:

where  ,
,  ,
,  ,
,  , and
, and  are sequences in
are sequences in  and
and  ,
,  are positive sequences. Assume that the control sequences satisfy the following restrictions:
are positive sequences. Assume that the control sequences satisfy the following restrictions:
(C1) ,
,
(C2) and
and  ,
,
(C3) ,
,
(C4) ,
,
(C5) ,
,  , where
, where  are two positive constants,
are two positive constants,
(C6) ,
,  and
and  , for some
, for some  .
.
Then,  converges strongly to a point
converges strongly to a point  which is the unique solution of the variational inequality
which is the unique solution of the variational inequality

or equivalent  , where
, where  is a metric projection mapping form
is a metric projection mapping form  onto
onto  .
.
Finally, we consider the following convex feasibility problem  :
:

where  is an integer and each
is an integer and each  is assumed to be the of solutions of equilibrium problem with the bifunction
is assumed to be the of solutions of equilibrium problem with the bifunction  and the solution set of the variational inequality problem. There is a considerable investigation on
and the solution set of the variational inequality problem. There is a considerable investigation on  in the setting of Hilbert spaces which captures applications in various disciplines such as image restoration [42, 43], computer tomography [44], and radiation therapy treatment planning [45].
in the setting of Hilbert spaces which captures applications in various disciplines such as image restoration [42, 43], computer tomography [44], and radiation therapy treatment planning [45].
The following result can be concluded from Theorem 3.1 easily.
Theorem 3.3.
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space  . Let be a
. Let be a  bifunction from
bifunction from  to
to  satisfying (A1)–(A4) and let
satisfying (A1)–(A4) and let  be a proper lower semicontinuous and convex function. Let
be a proper lower semicontinuous and convex function. Let  be an
be an  -inverse strongly monotone mapping for each
-inverse strongly monotone mapping for each  . Let
. Let  be a contraction mapping with coefficient
be a contraction mapping with coefficient  and let
and let  be a strongly positive linear bounded operator on
be a strongly positive linear bounded operator on  with coefficient
with coefficient  and
and  . Let
. Let  be a
be a  -strict pseudo-contraction with a fixed point. Define a mapping
-strict pseudo-contraction with a fixed point. Define a mapping  by
by  , for all
, for all  . Assume that
. Assume that

Assume that either  or
or  . Let
. Let  be a sequence generated by the following iterative algorithm:
be a sequence generated by the following iterative algorithm:

where  such that
such that  ,
,  are positive sequences and
are positive sequences and  ,
,  are sequences in
are sequences in  . Assume that the control sequences satisfy the following restrictions:
. Assume that the control sequences satisfy the following restrictions:
(C1) and
and  ,
,
(C2) ,
,
(C3) , for each
, for each  ,
,
(C4) , where
, where  is some positive constant for each
is some positive constant for each  ,
,
(C5) , for each
, for each  .
.
Then,  converges strongly to a point
converges strongly to a point  which is the unique solution of the variational inequality
which is the unique solution of the variational inequality

or equivalent  , where
, where  is a metric projection mapping form
is a metric projection mapping form  onto
onto  .
.
References
Takahashi W: Nonlinear Functional Analysis. Yokohama Publishers, Yokohama, Japan; 2000:iv+276.
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
Marino G, Xu H-K: Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,329(1):336–346. 10.1016/j.jmaa.2006.06.055
Zhou H: Convergence theorems of fixed points for -strict pseudo-contractions in Hilbert spaces. Nonlinear Analysis. Theory, Methods & Applications. Series A 2008,69(2):456–462. 10.1016/j.na.2007.05.032
Ceng L-C, Yao J-C: A hybrid iterative scheme for mixed equilibrium problems and fixed point problems. Journal of Computational and Applied Mathematics 2008,214(1):186–201. 10.1016/j.cam.2007.02.022
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994,63(1–4):123–145.
Yao JC, Chadli O: Pseudomonotone complementarity problems and variational inequalities. In Handbook of Generalized Convexity and Monotonicity Edited by: Crouzeix JP, Haddjissas N, Schaible S. 2005, 501–558.
Zeng LC, Schaible S, Yao JC: Iterative algorithm for generalized set-valued strongly nonlinear mixed variational-like inequalities. Journal of Optimization Theory and Applications 2005,124(3):725–738. 10.1007/s10957-004-1182-z
Aoyama K, Kimura Y, Takahashi W: Maximal monotone operators and maximal monotone functions for equilibrium problems. Journal of Convex Analysis 2008,15(2):395–409.
Combettes PL, Hirstoaga SA: Equilibrium programming using proximal-like algorithms. Mathematical Programming 1997,78(1):29–41.
Gao X, Guo Y: Strong convergence of a modified iterative algorithm for mixed-equilibrium problems in Hilbert spaces. Journal of Inequalities and Applications 2008, 2008:-23.
Jaiboon C, Kumam P: A hybrid extragradient viscosity approximation method for solving equilibrium problems and fixed point problems of infinitely many nonexpansive mappings. Fixed Point Theory and Applications 2009, 2009:-32.
Kumam P, Jaiboon C: A new hybrid iterative method for mixed equilibrium problems and variational inequality problem for relaxed cocoercive mappings with application to optimization problems. Nonlinear Analysis. Hybrid Systems 2009,3(4):510–530. 10.1016/j.nahs.2009.04.001
Jaiboon C, Kumam P: Strong convergence theorems for solving equilibrium problems and fixed point problems of -strict pseudo-contraction mappings by two hybrid projection methods. Journal of Computational and Applied Mathematics 2010,234(3):722–732. 10.1016/j.cam.2010.01.012
Jaiboon C, Kumam P, Humphries UW: Weak convergence theorem by an extragradient method for variational inequality, equilibrium and fixed point problems. Bulletin of the Malaysian Mathematical Sciences Society. Second Series 2009,32(2):173–185.
Kumam P, Jaiboon C: A system of generalized mixed equilibrium problems and fixed point problems for pseudocontractive mappings in Hilbert spaces. Fixed Point Theory and Applications 2010, 2010:-33.
Peng J-W, Yao J-C: Strong convergence theorems of iterative scheme based on the extragradient method for mixed equilibrium problems and fixed point problems. Mathematical and Computer Modelling 2009,49(9–10):1816–1828. 10.1016/j.mcm.2008.11.014
Qin X, Cho YJ, Kang SM: Convergence analysis on hybrid projection algorithms for equilibrium problems and variational inequality problems. Mathematical Modelling and Analysis 2009,14(3):335–351. 10.3846/1392-6292.2009.14.335-351
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,331(1):506–515. 10.1016/j.jmaa.2006.08.036
Takahashi S, Takahashi W: Strong convergence theorem for a generalized equilibrium problem and a nonexpansive mapping in a Hilbert space. Nonlinear Analysis. Theory, Methods & Applications 2008,69(3):1025–1033. 10.1016/j.na.2008.02.042
Takahashi W, Zembayashi K: Strong convergence theorem by a new hybrid method for equilibrium problems and relatively nonexpansive mappings. Fixed Point Theory and Applications 2008, 2008:-11.
Takahashi W, Zembayashi K: Strong and weak convergence theorems for equilibrium problems and relatively nonexpansive mappings in Banach spaces. Nonlinear Analysis. Theory, Methods & Applications 2009,70(1):45–57. 10.1016/j.na.2007.11.031
Yao Y, Liou Y-C, Yao J-C: A new hybrid iterative algorithm for fixed-point problems, variational inequality problems, and mixed equilibrium problems. Fixed Point Theory and Applications 2008, 2007:-15.
Yao Y, Liou Y-C, Wu Y-J: An extragradient method for mixed equilibrium problems and fixed point problems. Fixed Point Theory and Applications 2009, 2009:-15.
Gao X, Guo Y: Strong convergence of a modified iterative algorithm for mixed-equilibrium problems in Hilbert spaces. Journal of Inequalities and Applications 2008, 2008:-23.
Zeng W-Y, Huang N-J, Zhao C-W: Viscosity approximation methods for generalized mixed equilibrium problems and fixed points of a sequence of nonexpansive mappings. Fixed Point Theory and Applications 2008, 2008:-15.
Yao Y, Liou Y-C, Yao J-C: A new hybrid iterative algorithm for fixed-point problems, variational inequality problems, and mixed equilibrium problems. Fixed Point Theory and Applications 2008, 2008:-15.
Rockafellar RT: On the maximality of sums of nonlinear monotone operators. Transactions of the American Mathematical Society 1970, 149: 75–88. 10.1090/S0002-9947-1970-0282272-5
Takahashi W, Toyoda M: Weak convergence theorems for nonexpansive mappings and monotone mappings. Journal of Optimization Theory and Applications 2003,118(2):417–428. 10.1023/A:1025407607560
Yao Y, Yao J-C: On modified iterative method for nonexpansive mappings and monotone mappings. Applied Mathematics and Computation 2007,186(2):1551–1558. 10.1016/j.amc.2006.08.062
Marino G, Xu H-K: A general iterative method for nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2006,318(1):43–52. 10.1016/j.jmaa.2005.05.028
Plubtieng S, Punpaeng R: A general iterative method for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,336(1):455–469. 10.1016/j.jmaa.2007.02.044
Liu Y: A general iterative method for equilibrium problems and strict pseudo-contractions in Hilbert spaces. Nonlinear Analysis. Theory, Methods & Applications. Series A 2009,71(10):4852–4861. 10.1016/j.na.2009.03.060
Wangkeeree R, Wangkeeree R: A general iterative method for variational inequality problems, mixed equilibrium problems, and fixed point problems of strictly pseudocontractive mappings in Hilbert spaces. Fixed Point Theory and Applications 2009, 2009:-32.
Qin X, Cho YJ, Kang SM: Viscosity approximation methods for generalized equilibrium problems and fixed point problems with applications. Nonlinear Analysis. Theory, Methods & Applications 2010,72(1):99–112. 10.1016/j.na.2009.06.042
Osilike MO, Igbokwe DI: Weak and strong convergence theorems for fixed points of pseudocontractions and solutions of monotone type operator equations. Computers & Mathematics with Applications 2000,40(4–5):559–567. 10.1016/S0898-1221(00)00179-6
Browder FE: Nonlinear operators and nonlinear equations of evolution in Banach spaces. Proceedings of Symposia in Pure Mathematics 1976, 18: 78–81.
Bruck RE Jr.: Properties of fixed-point sets of nonexpansive mappings in Banach spaces. Transactions of the American Mathematical Society 1973, 179: 251–262.
Peng J-W, Yao J-C: A new hybrid-extragradient method for generalized mixed equilibrium problems, fixed point problems and variational inequality problems. Taiwanese Journal of Mathematics 2008,12(6):1401–1432.
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals. Journal of Mathematical Analysis and Applications 2005,305(1):227–239. 10.1016/j.jmaa.2004.11.017
Xu H-K: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004,298(1):279–291. 10.1016/j.jmaa.2004.04.059
Combettes PL: The convex feasibility problemml: in image recovery. In Advances in Imaging and Electron Physics. Volume 95. Edited by: Hawkes P. Academic Press, Orlando, Fla, USA; 1996:155–270.
Kotzer T, Cohen N, Shamir J: Images to ration by a novel method of parallel projection onto constraint sets. Optics Letters 1995, 20: 1172–1174. 10.1364/OL.20.001172
Sezan MI, Stark H: Application of convex projection theory to image recovery in tomograph and related areas. In Image Recovery: Theory and Application. Edited by: Stark H. Academic Press, Orlando, Fla, USA; 1987:155–270.
Censor Y, Zenios SA: Parallel Optimization, Numerical Mathematics and Scientific Computation. Oxford University Press, New York, NY, USA; 1997:xxviii+539.
Acknowledgments
The authors would like to thank the referees for their valuable suggestions to improve this paper. This work was supported by the Center of Excellence in Mathematics, the Commission on Higher Education, Thailand.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kumam, P., Jaiboon, C. Approximation of Common Solutions to System of Mixed Equilibrium Problems, Variational Inequality Problem, and Strict Pseudo-Contractive Mappings. Fixed Point Theory Appl 2011, 347204 (2011). https://doi.org/10.1155/2011/347204
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/347204
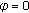 , then the mixed equilibrium problem (1.3) becomes to be the equilibrium problem which is to find
, then the mixed equilibrium problem (1.3) becomes to be the equilibrium problem which is to find  such that
such that 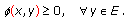
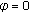 and
and 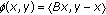 for all
for all 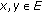 , where
, where  is a nonlinear mapping, then problem (1.5) becomes to be the variational inequality problems which is to find
is a nonlinear mapping, then problem (1.5) becomes to be the variational inequality problems which is to find 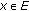 such that
such that 
 is called amonotone if, for all
is called amonotone if, for all  ,
, 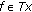 and
and 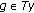 imply
imply  .
.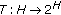 is a maximal if the graph of
is a maximal if the graph of 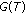 of
of 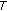 is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping
is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping  is maximal if and only if for
is maximal if and only if for  ,
, 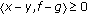 for every
for every  implies
implies  .
.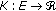 is
is 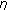 -strongly convex with constant
-strongly convex with constant 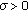 and its derivative
and its derivative 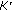 is sequentially continuous from weak topology to strong topology. We note that the condition (H) for the function
is sequentially continuous from weak topology to strong topology. We note that the condition (H) for the function 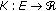 is a very strong condition. We also note that the condition (H) does not cover the case
is a very strong condition. We also note that the condition (H) does not cover the case  and
and 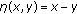 for each
for each 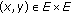 . Very recently, R. Wangkeeree and R. Wangkeeree [
. Very recently, R. Wangkeeree and R. Wangkeeree [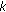 -strict pseudo-contraction mapping, and the set of solutions of the variational inequality for an inverse strongly monotone mapping in Hilbert spaces. They obtained a strong convergence theorem except the condition (H) for the sequences generated by these processes.
-strict pseudo-contraction mapping, and the set of solutions of the variational inequality for an inverse strongly monotone mapping in Hilbert spaces. They obtained a strong convergence theorem except the condition (H) for the sequences generated by these processes.