- Research Article
- Open access
- Published:
Common Coupled Fixed Point Theorems for Contractive Mappings in Fuzzy Metric Spaces
Fixed Point Theory and Applications volume 2011, Article number: 363716 (2011)
Abstract
We prove a common fixed point theorem for mappings under  -contractive conditions in fuzzy metric spaces. We also give an example to illustrate the theorem. The result is a genuine generalization of the corresponding result of S.Sedghi et al. (2010)
-contractive conditions in fuzzy metric spaces. We also give an example to illustrate the theorem. The result is a genuine generalization of the corresponding result of S.Sedghi et al. (2010)
1. Introduction
Since Zadeh [1] introduced the concept of fuzzy sets, many authors have extensively developed the theory of fuzzy sets and applications. George and Veeramani [2, 3] gave the concept of fuzzy metric space and defined a Hausdorff topology on this fuzzy metric space which have very important applications in quantum particle physics particularly in connection with both string and  -infinity theory.
-infinity theory.
Bhaskar and Lakshmikantham [4], Lakshmikantham and Ćirić [5] discussed the mixed monotone mappings and gave some coupled fixed point theorems which can be used to discuss the existence and uniqueness of solution for a periodic boundary value problem. Sedghi et al. [6] gave a coupled fixed point theorem for contractions in fuzzy metric spaces, and Fang [7] gave some common fixed point theorems under  -contractions for compatible and weakly compatible mappings in Menger probabilistic metric spaces. Many authors [8–23] have proved fixed point theorems in (intuitionistic) fuzzy metric spaces or probabilistic metric spaces.
-contractions for compatible and weakly compatible mappings in Menger probabilistic metric spaces. Many authors [8–23] have proved fixed point theorems in (intuitionistic) fuzzy metric spaces or probabilistic metric spaces.
In this paper, using similar proof as in [7], we give a new common fixed point theorem under weaker conditions than in [6] and give an example which shows that the result is a genuine generalization of the corresponding result in [6].
2. Preliminaries
First we give some definitions.
Definition 1 (see [2]).
A binary operation  is continuous
is continuous  -norm if
-norm if  is satisfying the following conditions:
is satisfying the following conditions:
(1) is commutative and associative;
is commutative and associative;
(2) is continuous;
is continuous;
(3) for all
for all  ;
;
(4) whenever
whenever  and
and  for all
for all  .
.
Definition 2 (see [24]).
Let  . A
. A  -norm
-norm  is said to be of H-type if the family of functions
is said to be of H-type if the family of functions  is equicontinuous at
is equicontinuous at  , where
, where

The  -norm
-norm  is an example of
is an example of  -norm of H-type, but there are some other
-norm of H-type, but there are some other  -norms
-norms  of H-type [24].
of H-type [24].
Obviously,  is a H-type
is a H-type  norm if and only if for any
norm if and only if for any  , there exists
, there exists  such that
such that  for all
for all  , when
, when  .
.
Definition 3 (see [2]).
A 3-tuple  is said to be a fuzzy metric space if
is said to be a fuzzy metric space if  is an arbitrary nonempty set,
is an arbitrary nonempty set,  is a continuous
is a continuous  -norm, and
-norm, and  is a fuzzy set on
is a fuzzy set on  satisfying the following conditions, for each
satisfying the following conditions, for each  and
and  :
:
(FM-1) ;
;
(FM-2) if and only if
if and only if  ;
;
(FM-3) ;
;
(FM-4) ;
;
(FM-5) is continuous.
is continuous.
Let  be a fuzzy metric space. For
be a fuzzy metric space. For  , the open ball
, the open ball  with a center
with a center  and a radius
and a radius  is defined by
is defined by

A subset  is called open if, for each
is called open if, for each  , there exist
, there exist  and
and  such that
such that  . Let
. Let  denote the family of all open subsets of
denote the family of all open subsets of  . Then
. Then  is called the topology on
is called the topology on  induced by the fuzzy metric
induced by the fuzzy metric  . This topology is Hausdorff and first countable.
. This topology is Hausdorff and first countable.
Example 1.
Let  be a metric space. Define
be a metric space. Define  -norm
-norm  and for all
and for all  and
and  ,
,  . Then
. Then  is a fuzzy metric space. We call this fuzzy metric
is a fuzzy metric space. We call this fuzzy metric  induced by the metric
induced by the metric  the standard fuzzy metric.
the standard fuzzy metric.
Definition 4 (see [2]).
Let  be a fuzzy metric space, then
be a fuzzy metric space, then
(1)a sequence  in
in  is said to be convergent to
is said to be convergent to  (denoted by
(denoted by  ) if
) if

for all  ;
;
(2)a sequence  in
in  is said to be a Cauchy sequence if for any
is said to be a Cauchy sequence if for any  , there exists
, there exists  , such that
, such that

for all  and
and  ;
;
(3)a fuzzy metric space  is said to be complete if and only if every Cauchy sequence in
is said to be complete if and only if every Cauchy sequence in  is convergent.
is convergent.
Remark 1 (see [25]).
-
(1)
For all
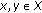 ,
, 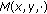 is nondecreasing.
is nondecreasing. -
(2)
It is easy to prove that if
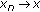 ,
,  ,
,  , then
, then 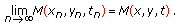 (2.5)
(2.5)
-
(3)
In a fuzzy metric space
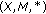 , whenever
, whenever 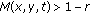 for
for  in
in 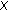 ,
, 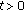 ,
, 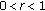 , we can find a
, we can find a 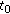 ,
, 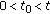 such that
such that  .
. -
(4)
For any
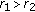 , we can find an
, we can find an 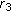 such that
such that 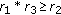 and for any
and for any  we can find a
we can find a 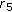 such that
such that 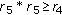
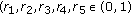 ).
).
Definition 5 (see [6]).
Let  be a fuzzy metric space.
be a fuzzy metric space.  is said to satisfy the
is said to satisfy the  -property on
-property on  if
if

whenever  ,
,  and
and  .
.
Lemma 1.
Let  be a fuzzy metric space and
be a fuzzy metric space and  satisfies the
satisfies the  -property; then
-property; then

Proof.
If not, since  is nondecreasing and
is nondecreasing and  , there exists
, there exists  such that
such that  , then for
, then for  ,
,  when
when  as
as  and we get
and we get  , which is a contraction.
, which is a contraction.
Remark 2.
Condition (2.7) cannot guarantee the  -property. See the following example.
-property. See the following example.
Example 2.
Let  be an ordinary metric space,
be an ordinary metric space,  for all
for all  , and
, and  be defined as following:
be defined as following:

where  . Then
. Then  is continuous and increasing in
is continuous and increasing in  ,
,  and
and  . Let
. Let

then  is a fuzzy metric space and
is a fuzzy metric space and

But for any  ,
,  ,
,  ,
,  ,
,

Define  , where
, where  and each
and each  satisfies the following conditions:
satisfies the following conditions:
(-1) is nondecreasing;
is nondecreasing;
(-2) is upper semicontinuous from the right;
is upper semicontinuous from the right;
(-3) for all
for all  , where
, where  ,
,  .
.
It is easy to prove that, if  , then
, then  for all
for all  .
.
Lemma 2 (see [7]).
Let  be a fuzzy metric space, where
be a fuzzy metric space, where  is a continuous
is a continuous  -norm of H-type. If there exists
-norm of H-type. If there exists  such that if
such that if

for all  , then
, then  .
.
Definition 6 (see [5]).
An element  is called a coupled fixed point of the mapping
is called a coupled fixed point of the mapping  if
if

Definition 7 (see [5]).
An element  is called a coupled coincidence point of the mappings
is called a coupled coincidence point of the mappings  and
and  if
if

Definition 8 (see [7]).
An element  is called a common coupled fixed point of the mappings
is called a common coupled fixed point of the mappings  and
and  if
if

Definition 9 (see [7]).
An element  is called a common fixed point of the mappings
is called a common fixed point of the mappings  and
and  if
if

Definition 10 (see [7]).
The mappings  and
and  are said to be compatible if
are said to be compatible if

for all  whenever
whenever  and
and  are sequences in
are sequences in  , such that
, such that

for all  are satisfied.
are satisfied.
Definition 11 (see [7]).
The mappings  and
and  are called commutative if
are called commutative if

for all  .
.
Remark 3.
It is easy to prove that, if  and
and  are commutative, then they are compatible.
are commutative, then they are compatible.
3. Main Results
For convenience, we denote

for all  .
.
Theorem 1.
Let  be a complete FM-space, where
be a complete FM-space, where  is a continuous
is a continuous  -norm of H-type satisfying (2.7). Let
-norm of H-type satisfying (2.7). Let  and
and  be two mappings and there exists
be two mappings and there exists  such that
such that

for all  ,
,  .
.
Suppose that  , and
, and  is continuous,
is continuous,  and
and  are compatible. Then there exist
are compatible. Then there exist  such that
such that  , that is,
, that is,  and
and  have a unique common fixed point in
have a unique common fixed point in  .
.
Proof.
Let  be two arbitrary points in
be two arbitrary points in  . Since
. Since  , we can choose
, we can choose  such that
such that  and
and  . Continuing in this way we can construct two sequences
. Continuing in this way we can construct two sequences  and
and  in
in  such that
such that

The proof is divided into 4 steps.
Step 1.
Prove that  and
and  are Cauchy sequences.
are Cauchy sequences.
Since  is a
is a  -norm of H-type, for any
-norm of H-type, for any  , there exists a
, there exists a  such that
such that

for all  .
.
Since  is continuous and
is continuous and  for all
for all  , there exists
, there exists  such that
such that

On the other hand, since  , by condition (
, by condition ( ) we have
) we have  . Then for any
. Then for any  , there exists
, there exists  such that
such that

From condition (3.2), we have

Similarly, we can also get

Continuing in the same way we can get

So, from (3.5) and (3.6), for  , we have
, we have

which implies that

for all  with
with  and
and  . So
. So  is a Cauchy sequence.
is a Cauchy sequence.
Similarly, we can get that  is also a Cauchy sequence.
is also a Cauchy sequence.
Step 2.
Prove that  and
and  have a coupled coincidence point.
have a coupled coincidence point.
Since  complete, there exist
complete, there exist  such that
such that

Since  and
and  are compatible, we have by (3.12),
are compatible, we have by (3.12),

for all  . Next we prove that
. Next we prove that  and
and  .
.
For all  , by condition (3.2), we have
, by condition (3.2), we have

for all  . Let
. Let  , since
, since  and
and  are compatible, with the continuity of
are compatible, with the continuity of  , we get
, we get

which implies that  . Similarly, we can get
. Similarly, we can get  .
.
Step 3.
Prove that  and
and  .
.
Since  is a
is a  -norm of H-type, for any
-norm of H-type, for any  , there exists an
, there exists an  such that
such that

for all  .
.
Since  is continuous and
is continuous and  for all
for all  , there exists
, there exists  such that
such that  and
and  .
.
On the other hand, since  , by condition
, by condition  we have
we have  . Then for any
. Then for any  , there exists
, there exists  such that
such that  . Since
. Since

letting  , we get
, we get

Similarly, we can get

From (3.18) and (3.19) we have

By this way, we can get for all  ,
,

Then, we have

So for any  we have
we have

for all  . We can get that
. We can get that  and
and  .
.
Step 4.
Prove that  .
.
Since  is a
is a  -norm of H-type, for any
-norm of H-type, for any  , there exists an
, there exists an  such that
such that

for all  .
.
Since  is continuous and
is continuous and  , there exists
, there exists  such that
such that  .
.
On the other hand, since  , by condition
, by condition  we have
we have  . Then for any
. Then for any  , there exists
, there exists  such that
such that  .
.
Since for  ,
,

Letting  yields
yields

Thus we have

which implies that  .
.
Thus we have proved that  and
and  have a unique common fixed point in
have a unique common fixed point in  .
.
This completes the proof of the Theorem 1.
Taking  (the identity mapping) in Theorem 1, we get the following consequence.
(the identity mapping) in Theorem 1, we get the following consequence.
Corollary 1.
Let  be a complete FM-space, where
be a complete FM-space, where  is a continuous
is a continuous  -norm of H-type satisfying (2.7). Let
-norm of H-type satisfying (2.7). Let  and there exists
and there exists  such that
such that

for all  ,
,  .
.
Then there exist  such that
such that  , that is,
, that is,  admits a unique fixed point in
admits a unique fixed point in  .
.
Let  , where
, where  , the following by Lemma 1, we get the following.
, the following by Lemma 1, we get the following.
Corollary 2 (see [6]).
Let  for all
for all  and
and  be a complete fuzzy metric space such that
be a complete fuzzy metric space such that  has
has  -property. Let
-property. Let  and
and  be two functions such that
be two functions such that

for all  , where
, where  ,
,  and
and  is continuous and commutes with
is continuous and commutes with  . Then there exists a unique
. Then there exists a unique  such that
such that  .
.
Next we give an example to demonstrate Theorem 1.
Example 3.
Let  ,
,  for all
for all  .
.  is defined as (2.8). Let
is defined as (2.8). Let

for all  . Then
. Then  is a complete FM-space.
is a complete FM-space.
Let  ,
,  and
and  be defined as
be defined as

Then  satisfies all the condition of Theorem 1, and there exists a point
satisfies all the condition of Theorem 1, and there exists a point  which is the unique common fixed point of
which is the unique common fixed point of  and
and  .
.
In fact, it is easy to see that  ,
,

For all  and
and  . (3.28) is equivalent to
. (3.28) is equivalent to

Since  , we can get
, we can get

From (3.33), we only need to verify the following:

that is,

We consider the following cases.
Case 1 ( ).
).
Then (3.36) is equivalent to

it is easy to verified.
Case 2 ( ).
).
Then (3.36) is equivalent to

which is

since

that is

holds for all  . So (3.36) holds for
. So (3.36) holds for  .
.
Case 3 ( ).
).
Then (3.36) is equivalent to

Let  , we only need to verify
, we only need to verify

for all  that
that  . We can verify it holds.
. We can verify it holds.
Thus it is verified that the functions  ,
,  ,
,  satisfy all the conditions of Theorem 1;
satisfy all the conditions of Theorem 1;  is the common fixed point of
is the common fixed point of  and
and  in
in  .
.
References
Zadeh LA: Fuzzy sets. Information and Computation 1965, 8: 338–353.
George A, Veeramani P: On some results in fuzzy metric spaces. Fuzzy Sets and Systems 1994,64(3):395–399. 10.1016/0165-0114(94)90162-7
George A, Veeramani P: On some results of analysis for fuzzy metric spaces. Fuzzy Sets and Systems 1997,90(3):365–368. 10.1016/S0165-0114(96)00207-2
Bhaskar TG, Lakshmikantham V: Fixed point theorems in partially ordered metric spaces and applications. Nonlinear Analysis. Theory, Methods & Applications 2006,65(7):1379–1393. 10.1016/j.na.2005.10.017
Lakshmikantham V, Ćirić L: Coupled fixed point theorems for nonlinear contractions in partially ordered metric spaces. Nonlinear Analysis. Theory, Methods & Applications 2009,70(12):4341–4349. 10.1016/j.na.2008.09.020
Sedghi S, Altun I, Shobe N: Coupled fixed point theorems for contractions in fuzzy metric spaces. Nonlinear Analysis. Theory, Methods & Applications 2010,72(3–4):1298–1304. 10.1016/j.na.2009.08.018
Fang J-X: Common fixed point theorems of compatible and weakly compatible maps in Menger spaces. Nonlinear Analysis. Theory, Methods & Applications 2009,71(5–6):1833–1843. 10.1016/j.na.2009.01.018
Ćirić LB, Miheţ D, Saadati R: Monotone generalized contractions in partially ordered probabilistic metric spaces. Topology and its Applications 2009,156(17):2838–2844. 10.1016/j.topol.2009.08.029
O'Regan D, Saadati R: Nonlinear contraction theorems in probabilistic spaces. Applied Mathematics and Computation 2008,195(1):86–93. 10.1016/j.amc.2007.04.070
Jain S, Jain S, Bahadur Jain L: Compatibility of type (P) in modified intuitionistic fuzzy metric space. Journal of Nonlinear Science and its Applications 2010,3(2):96–109.
Ćirić LB, Ješić SN, Ume JS: The existence theorems for fixed and periodic points of nonexpansive mappings in intuitionistic fuzzy metric spaces. Chaos, Solitons and Fractals 2008,37(3):781–791. 10.1016/j.chaos.2006.09.093
\'Cirić L, Lakshmikantham V: Coupled random fixed point theorems for nonlinear contractions in partially ordered metric spaces. Stochastic Analysis and Applications 2009,27(6):1246–1259. 10.1080/07362990903259967
Ćirić L, Cakić N, Rajović M, Ume JS: Monotone generalized nonlinear contractions in partially ordered metric spaces. Fixed Point Theory and Applications 2008, 2008:-11.
Aliouche A, Merghadi F, Djoudi A: A related fixed point theorem in two fuzzy metric spaces. Journal of Nonlinear Science and its Applications 2009,2(1):19–24.
Ćirić L: Common fixed point theorems for a family of non-self mappings in convex metric spaces. Nonlinear Analysis. Theory, Methods & Applications 2009,71(5–6):1662–1669. 10.1016/j.na.2009.01.002
Rao KPR, Aliouche A, Babu GR: Related fixed point theorems in fuzzy metric spaces. Journal of Nonlinear Science and its Applications 2008,1(3):194–202.
Ćirić L, Cakić N: On common fixed point theorems for non-self hybrid mappings in convex metric spaces. Applied Mathematics and Computation 2009,208(1):90–97. 10.1016/j.amc.2008.11.012
Ćirić L: Some new results for Banach contractions and Edelstein contractive mappings on fuzzy metric spaces. Chaos, Solitons and Fractals 2009,42(1):146–154. 10.1016/j.chaos.2008.11.010
Shakeri S, Ćirić LJB, Saadati R: Common fixed point theorem in partially ordered -fuzzy metric spaces. Fixed Point Theory and Applications 2010, 2010:-13.
Ćirić L, Samet B, Vetro C: Common fixed point theorems for families of occasionally weakly compatible mappings. Mathematical and Computer Modelling 2011,53(5–6):631–636. 10.1016/j.mcm.2010.09.015
Ćirić L, Abbas M, Saadati R, Hussain N: Common fixed points of almost generalized contractive mappings in ordered metric spaces. Applied Mathematics and Computation 2011,217(12):5784–5789. 10.1016/j.amc.2010.12.060
Ćirić L, Abbas M, Damjanović B, Saadati R: Common fuzzy fixed point theorems in ordered metric spaces. Mathematical and Computer Modelling 2011,53(9–10):1737–1741. 10.1016/j.mcm.2010.12.050
Kamran T, Cakić N: Hybrid tangential property and coincidence point theorems. Fixed Point Theory 2008,9(2):487–496.
Hadžić O, Pap E: Fixed Point Theory in Probabilistic Metric Spaces, Mathematics and its Applications. Volume 536. Kluwer Academic, Dordrecht, The Netherlands; 2001:x+273.
Grabiec M: Fixed points in fuzzy metric spaces. Fuzzy Sets and Systems 1988,27(3):385–389. 10.1016/0165-0114(88)90064-4
Acknowledgment
The author is grateful to the referees for their valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hu, XQ. Common Coupled Fixed Point Theorems for Contractive Mappings in Fuzzy Metric Spaces. Fixed Point Theory Appl 2011, 363716 (2011). https://doi.org/10.1155/2011/363716
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/363716
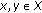 ,
, 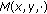 is nondecreasing.
is nondecreasing.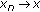 ,
,  ,
,  , then
, then 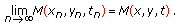
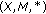 , whenever
, whenever 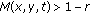 for
for  in
in 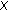 ,
, 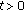 ,
, 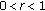 , we can find a
, we can find a 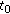 ,
, 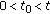 such that
such that  .
.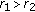 , we can find an
, we can find an 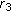 such that
such that 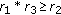 and for any
and for any  we can find a
we can find a 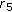 such that
such that 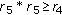
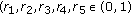 ).
).