- Research Article
- Open access
- Published:
Systems of Generalized Quasivariational Inclusion Problems with Applications in  -Spaces
-Spaces
Fixed Point Theory and Applications volume 2011, Article number: 561573 (2011)
Abstract
We first prove that the product of a family of  -spaces is also an
-spaces is also an  -space. Then, by using a Himmelberg type fixed point theorem in
-space. Then, by using a Himmelberg type fixed point theorem in  -spaces, we establish existence theorems of solutions for systems of generalized quasivariational inclusion problems, systems of variational equations, and systems of generalized quasiequilibrium problems in
-spaces, we establish existence theorems of solutions for systems of generalized quasivariational inclusion problems, systems of variational equations, and systems of generalized quasiequilibrium problems in  -spaces. Applications of the existence theorem of solutions for systems of generalized quasiequilibrium problems to optimization problems are given in
-spaces. Applications of the existence theorem of solutions for systems of generalized quasiequilibrium problems to optimization problems are given in  -spaces.
-spaces.
1. Introduction
In 1979, Robinson [1] studied the following parametric variational inclusion problem: given  , find
, find  such that
such that

where  is a single-valued function and
is a single-valued function and  is a multivalued map. It is known that (1.1) covers variational inequality problems and a vast of variational system important in applications. Since then, various types of variational inclusion problems have been extended and generalized by many authors (see, e.g., [2–7] and the references therein).
is a multivalued map. It is known that (1.1) covers variational inequality problems and a vast of variational system important in applications. Since then, various types of variational inclusion problems have been extended and generalized by many authors (see, e.g., [2–7] and the references therein).
On the other hand, Tarafdar [8] generalized the classical Himmelberg fixed point theorem [9] to locally  -convex uniform spaces (or
-convex uniform spaces (or  -spaces). Park [10] generalized the result of Tarafdar [8] to locally
-spaces). Park [10] generalized the result of Tarafdar [8] to locally  -convex spaces (or
-convex spaces (or  -spaces). Recently, Park [11] introduced the concept of abstract convex spaces which include
-spaces). Recently, Park [11] introduced the concept of abstract convex spaces which include  -spaces and
-spaces and  -convex spaces as special cases. With this new concept, he can study the KKM theory and its applications in abstract convex spaces. More recently, Park [12] introduced the concept of
-convex spaces as special cases. With this new concept, he can study the KKM theory and its applications in abstract convex spaces. More recently, Park [12] introduced the concept of  -spaces which include
-spaces which include  -spaces and
-spaces and  -spaces as special cases. He also established the Himmelberg type fixed point theorem in
-spaces as special cases. He also established the Himmelberg type fixed point theorem in  -spaces. To see some related works, we refer to [13–21] and the references therein. However, to the best of our knowledge, there is no paper dealing with systems of generalized quasivariational inclusion problems in
-spaces. To see some related works, we refer to [13–21] and the references therein. However, to the best of our knowledge, there is no paper dealing with systems of generalized quasivariational inclusion problems in  -spaces.
-spaces.
Motivated and inspired by the works mentioned above, in this paper, we first prove that the product of a family of  -spaces is also an
-spaces is also an  -space. Then, by using the Himmelberg type fixed point theorem due to Park [12], we establish existence theorems of solutions for systems of generalized quasivariational inclusion problems, systems of variational equations, and systems of generalized quasiequilibrium problems in
-space. Then, by using the Himmelberg type fixed point theorem due to Park [12], we establish existence theorems of solutions for systems of generalized quasivariational inclusion problems, systems of variational equations, and systems of generalized quasiequilibrium problems in  -spaces. Applications of the existence theorem of solutions for systems of generalized quasiequilibrium problems to optimization problems are given in
-spaces. Applications of the existence theorem of solutions for systems of generalized quasiequilibrium problems to optimization problems are given in  -spaces.
-spaces.
2. Preliminaries
For a set  ,
,  will denote the family of all nonempty finite subsets of
will denote the family of all nonempty finite subsets of  . If
. If  is a subset of a topological space, we denote by int
is a subset of a topological space, we denote by int and
and  the interior and closure of
the interior and closure of  , respectively.
, respectively.
A multimap (or simply a map)  is a function from a set
is a function from a set  into the power set
into the power set  of
of  ; that is, a function with the values
; that is, a function with the values  for all
for all  . Given a map
. Given a map  , the map
, the map  defined by
defined by  for all
for all  , is called the (lower) inverse of
, is called the (lower) inverse of  . For any
. For any  ,
,  . For any
. For any  ,
,  . As usual, the set
. As usual, the set  is called the graph of
is called the graph of  .
.
For topological spaces  and
and  , a map
, a map  is called
is called
(i)closed if its graph  is a closed subset of
is a closed subset of  ,
,
(ii)upper semicontinuous (in short, u.s.c.) if for any  and any open set
and any open set  in
in  with
with  , there exists a neighborhood
, there exists a neighborhood  of
of  such that
such that  for all
for all  ,
,
(iii)lower semicontinuous (in short, l.s.c.) if for any  and any open set
and any open set  in
in  with
with  , there exists a neighborhood
, there exists a neighborhood  of
of  such that
such that  for all
for all  ,
,
(iv)continuous if  is both u.s.c. and l.s.c.,
is both u.s.c. and l.s.c.,
(v)compact if  is contained in a compact subset of
is contained in a compact subset of  .
.
Lemma 2.1 . (see [22]).
Let  and
and  be topological spaces,
be topological spaces,  be a map. Then,
be a map. Then,  is l.s.c. at
is l.s.c. at  if and only if for any
if and only if for any  and for any net
and for any net  in
in  converging to
converging to  , there exists a net
, there exists a net  in
in  such that
such that  for each
for each  and
and  converges to
converges to  .
.
Lemma 2.2 . (see [23]).
Let  and
and  be Hausdorff topological spaces and
be Hausdorff topological spaces and  be a map.
be a map.
(i)If  is an u.s.c. map with closed values, then
is an u.s.c. map with closed values, then  is closed.
is closed.
-
(ii)
If
 is a compact space and
is a compact space and 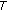 is closed, then
is closed, then 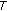 is u.s.c.
is u.s.c. -
(iii)
If
 is compact and
is compact and 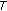 is an u.s.c. map with compact values, then
is an u.s.c. map with compact values, then 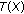 is compact.
is compact.
In what follows, we introduce the concept of abstract convex spaces and map classes  ,
,  and
and  having certain KKM properties. For more details and discussions, we refer the reader to [11, 12, 24].
having certain KKM properties. For more details and discussions, we refer the reader to [11, 12, 24].
Definition 2.3 (see [11]).
An abstract convex space  consists of a topological space
consists of a topological space  , a nonempty set
, a nonempty set  , and a map
, and a map  with nonempty values. We denote
with nonempty values. We denote  for
for  .
.
In the case  , let
, let  . It is obvious that any vector space
. It is obvious that any vector space  is an abstract convex space with
is an abstract convex space with  , where co denotes the convex hull in vector spaces. In particular,
, where co denotes the convex hull in vector spaces. In particular,  is an abstract convex space.
is an abstract convex space.
Let  be an abstract convex space. For any
be an abstract convex space. For any  , the
, the  -convex hull of
-convex hull of  is denoted and defined by
is denoted and defined by

(co is reserved for the convex hull in vector spaces). A subset  of
of  is called a
is called a  -convex subset of
-convex subset of  relative to
relative to  if for any
if for any  , we have
, we have  ; that is, co
; that is, co . This means that
. This means that  itself is an abstract convex space called a subspace of
itself is an abstract convex space called a subspace of  . When
. When  , the space is denoted by
, the space is denoted by  . In such case, a subset
. In such case, a subset  of
of  is said to be
is said to be  -convex if co
-convex if co ; in other words,
; in other words,  is
is  -convex relative to
-convex relative to  . When
. When  ,
,  -convex subsets reduce to ordinary convex subsets.
-convex subsets reduce to ordinary convex subsets.
Let  be an abstract convex space and
be an abstract convex space and  a set. For a map
a set. For a map  with nonempty values, if a map
with nonempty values, if a map  satisfies
satisfies

then  is called a KKM map with respect to
is called a KKM map with respect to  . A KKM map
. A KKM map  is a KKM map with respect to the identity map
is a KKM map with respect to the identity map  . A map
. A map  is said to have the KKM property and called a
is said to have the KKM property and called a  -map if, for any KKM map
-map if, for any KKM map  with respect to
with respect to  , the family
, the family  has the finite intersection property. We denote
has the finite intersection property. We denote

Similarly, when  is a topological space, a
is a topological space, a  -map is defined for closed-valued maps
-map is defined for closed-valued maps  , and a
, and a  -map is defined for open-valued maps
-map is defined for open-valued maps  . In this case, we have
. In this case, we have

Note that if  is discrete, then three classes
is discrete, then three classes  ,
,  and
and  are identical. Some authors use the notation
are identical. Some authors use the notation  instead of
instead of  .
.
Definition 2.4 . (see [24]).
For an abstract convex space  , the KKM principle is the statement
, the KKM principle is the statement  .
.
A KKM space is an abstract convex space satisfying the KKM principle.
Definition 2.5.
Let  be an abstract convex space,
be an abstract convex space,  be a real t.v.s., and
be a real t.v.s., and  a map. Then,
a map. Then,
 is
is  -quasiconvex-like if for any
-quasiconvex-like if for any  and any
and any  there exists
there exists  such that
such that  ,
,
 is
is  -quasiconvex if for any
-quasiconvex if for any  and any
and any  there exists
there exists  such that
such that  .
.
Remark 2.6.
If  is a nonempty convex subset of a t.v.s. with
is a nonempty convex subset of a t.v.s. with  , then Definition 2.5 (i) and (ii) reduce to Definition 2.4 (iii) and (vi) in Lin [5], respectively.
, then Definition 2.5 (i) and (ii) reduce to Definition 2.4 (iii) and (vi) in Lin [5], respectively.
Definition 2.7 . (see [25]).
A uniformity for a set  is a nonempty family
is a nonempty family  of subsets of
of subsets of  satisfying the following conditions:
satisfying the following conditions:
each member of  contains the diagonal
contains the diagonal  ,
,
for each  ,
,  ,
,
for each  , there exists
, there exists  such that
such that  ,
,
if  ,
,  , then
, then  ,
,
if  and
and  , then
, then  .
.
The pair  is called a uniform space. Every member in
is called a uniform space. Every member in  is called an entourage. For any
is called an entourage. For any  and any
and any  , we define
, we define  . The uniformity
. The uniformity  is called separating if
is called separating if  . The uniform space
. The uniform space  is Hausdorff if and only if
is Hausdorff if and only if  is separating. For more details about uniform spaces, we refer the reader to Kelley [25].
is separating. For more details about uniform spaces, we refer the reader to Kelley [25].
Definition 2.8 . (see [12]).
An abstract convex uniform space  is an abstract convex space with a basis
is an abstract convex space with a basis  of a uniformity of
of a uniformity of  .
.
Definition 2.9 . (see [12]).
An abstract convex uniform space  is called an
is called an  -space if
-space if
 is dense in
is dense in  , and
, and
for each  and each
and each  -convex subset
-convex subset  , the set
, the set  is
is  -convex.
-convex.
Lemma 2.10 . (see [12, Corollary  ]).
]).
Let  be a Hausdorff KKM
be a Hausdorff KKM  -space and
-space and  a compact u.s.c. map with nonempty closed
a compact u.s.c. map with nonempty closed  -convex values. Then,
-convex values. Then,  has a fixed point.
has a fixed point.
Lemma 2.11 . (see [24, Lemma  ]).
]).
Let  be any family of abstract convex spaces. Let
be any family of abstract convex spaces. Let  and
and  . For each
. For each  , let
, let  be the projection. For each
be the projection. For each  , define
, define  . Then,
. Then,  is an abstract convex space.
is an abstract convex space.
Lemma 2.12.
Let  be any index set. For each
be any index set. For each  , let
, let  be an
be an  -space. If one defines
-space. If one defines  ,
,  for each
for each  and
and  , where
, where  . Then,
. Then,  is also an
is also an  -space.
-space.
Proof.
By Lemma 2.11,  is an abstract convex space. It is easy to check that
is an abstract convex space. It is easy to check that  is a subbase of the product uniformity of
is a subbase of the product uniformity of  . Since
. Since  is the basis generated by
is the basis generated by  , we obtain that
, we obtain that  is a basis of the product uniformity, and the associated uniform topology on
is a basis of the product uniformity, and the associated uniform topology on  .
.
Now, we prove that for each  and each
and each  -convex subset
-convex subset  , the set
, the set  is
is  -convex. Firstly, we show that for each
-convex. Firstly, we show that for each  ,
,  is a
is a  -convex subset of
-convex subset of  . For any
. For any  , we can find some
, we can find some  with
with  . Since
. Since  is a
is a  -convex subset of
-convex subset of  , we have
, we have  . It follows that
. It follows that  . Thus, we have shown that
. Thus, we have shown that  is a
is a  -convex subset of
-convex subset of  . Secondly, we show that the set
. Secondly, we show that the set  is
is  -convex. Since each
-convex. Since each  has the form
has the form  for some
for some  and
and  , we have that
, we have that


By the definition of  -spaces, we obtain that for each
-spaces, we obtain that for each  , the set
, the set  is
is  -convex. It follows from (2.6) that the set
-convex. It follows from (2.6) that the set  is a
is a  -convex subset of
-convex subset of  . Therefore
. Therefore  is an
is an  -space. This completes the proof.
-space. This completes the proof.
Remark 2.13.
Lemma 2.12 generalizes [26, Theorem  ] from locally
] from locally  -uniform spaces to
-uniform spaces to  -spaces. The proof of Lemma 2.12 is different with the proof of [26, Theorem
-spaces. The proof of Lemma 2.12 is different with the proof of [26, Theorem  ].
].
3. Existence Theorems of Solutions for Systems of Generalized Quasivariational Inclusion Problems
Let  be any index set. For each
be any index set. For each  , let
, let  be a topological vector space,
be a topological vector space,  be an
be an  -space, and
-space, and  be an
be an  -space with
-space with  . Let
. Let  ,
,  and
and  be the product
be the product  -space as defined in Lemma 2.12. Furthermore, we assume that
-space as defined in Lemma 2.12. Furthermore, we assume that  is a KKM space. Throughout this paper, we use these notations unless otherwise specified, and assume that all topological spaces are Hausdorff.
is a KKM space. Throughout this paper, we use these notations unless otherwise specified, and assume that all topological spaces are Hausdorff.
The following theorem is the main result of this paper.
Theorem 3.1.
For each  , suppose that
, suppose that
(i) is a compact u.s.c. map with nonempty closed
is a compact u.s.c. map with nonempty closed  -convex values,
-convex values,
(ii) is a compact continuous map with nonempty closed
is a compact continuous map with nonempty closed  -convex values,
-convex values,
(iii) is a closed map with nonempty values,
is a closed map with nonempty values,
-
(iv)
for each
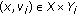 ,
, 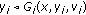 is
is  -quasiconvex; for each
-quasiconvex; for each 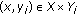 ,
, 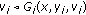 is
is  -quasiconvex-like and
-quasiconvex-like and  .
.
Then, there exists  with
with  and
and  such that for each
such that for each  ,
,  ,
,  and
and  for all
for all  .
.
Proof.
For each  , define
, define  by
by

Then,  is nonempty for each
is nonempty for each  . Indeed, fix any
. Indeed, fix any  and
and  , define
, define  by
by

First, we show that  is a KKM map w.r.t.
is a KKM map w.r.t.  . Suppose to the contrary that there exists a finite subset
. Suppose to the contrary that there exists a finite subset 
 such that
such that  . Hence, there exists
. Hence, there exists  satisfying
satisfying  for all
for all  . Since
. Since  is
is  -convex, we have
-convex, we have  . By
. By  for all
for all  , we know that
, we know that  for all
for all  . Since
. Since  is
is  -quasiconvex-like, there exists
-quasiconvex-like, there exists  such that
such that

This leads to a contradiction. Therefore,  is a KKM map w.r.t.
is a KKM map w.r.t.  . Next, we show that
. Next, we show that  is closed for each
is closed for each  . Indeed, if
. Indeed, if  , then there exists a net
, then there exists a net  in
in  such that
such that  . For each
. For each  , we have
, we have  and
and  . By condition (ii),
. By condition (ii),  is closed, and hence
is closed, and hence  . By condition (iii),
. By condition (iii),  is closed, and hence
is closed, and hence  . It follows that
. It follows that  . Therefore,
. Therefore,  is closed. Since
is closed. Since  and
and  is
is  -convex, we have that
-convex, we have that  . Having that
. Having that  is compact, we can deduce that
is compact, we can deduce that  . That is
. That is  is nonempty.
is nonempty.
 is closed for each
is closed for each  . Indeed, if
. Indeed, if  , then there exists a net
, then there exists a net  in
in  such that
such that  . One has
. One has  and
and  for all
for all  . By condition (ii),
. By condition (ii),  is closed, and hence
is closed, and hence  . Let
. Let  , since
, since  is l.s.c., there exists a net
is l.s.c., there exists a net  satisfying
satisfying  and
and  . We have
. We have  . Since
. Since  is closed, we obtain
is closed, we obtain  . Thus, we have shown that
. Thus, we have shown that  . Hence,
. Hence,  is closed.
is closed.
 is
is  -convex for each
-convex for each  and
and  . Indeed, if
. Indeed, if  , then we have that
, then we have that  and
and  for all
for all  and all
and all  . For any given
. For any given  , we have
, we have  because
because  is
is  -convex. For each
-convex. For each  , since
, since  is
is  -quasiconvex, there exists
-quasiconvex, there exists  such that
such that

Hence,  for all
for all  . It follows that
. It follows that  and
and  is
is  -convex.
-convex.
Since  and
and  is compact. It follows from Lemma 2.2(ii) that
is compact. It follows from Lemma 2.2(ii) that  is a compact u.s.c. map for each
is a compact u.s.c. map for each  . Define
. Define  by
by

It follows from the above discussions that for each  ,
,  is a compact u.s.c. map with nonempty closed
is a compact u.s.c. map with nonempty closed  -convex values. Thus,
-convex values. Thus,  is a compact u.s.c. map with nonempty closed
is a compact u.s.c. map with nonempty closed  -convex values. By Lemma 2.10, there exists
-convex values. By Lemma 2.10, there exists  such that
such that  . That is there exists
. That is there exists  with
with  and
and  such that for each
such that for each  ,
,  ,
,  and
and  for all
for all  . This completes the proof.
. This completes the proof.
For the special case of Theorem 3.1, we have the following corollary which is actually an existence theorem of solutions for variational equations.
Corollary 3.2.
For each  , suppose that conditions (i) and (ii) in Theorem 3.1 hold. Moreover,
, suppose that conditions (i) and (ii) in Theorem 3.1 hold. Moreover,
(iii)1 is a continuous mapping;
is a continuous mapping;
(iv)1 for each  ,
,  is
is  -quasiconvex; for each
-quasiconvex; for each  ,
,  is also
is also  -quasiconvex and
-quasiconvex and  .
.
Then, there exists  with
with  and
and  such that for each
such that for each  ,
,  ,
,  and
and  for all
for all  .
.
Theorem 3.3.
For each  , suppose that conditions (i) and (ii) in Theorem 3.1 hold. Moreover,
, suppose that conditions (i) and (ii) in Theorem 3.1 hold. Moreover,
(iii)2 is a closed map with nonempty values and
is a closed map with nonempty values and  is an u.s.c. map with nonempty compact values;
is an u.s.c. map with nonempty compact values;
(iv)2 for each  ,
,  is
is  -quasiconvex; for each
-quasiconvex; for each  ,
,  is
is  -quasiconvex-like and
-quasiconvex-like and  .
.
Then, there exists  with
with  and
and  such that for each
such that for each  ,
,  ,
,  and
and  for all
for all  .
.
Proof.
For each  , define
, define  by
by

Obviously,  has nonempty values. Now, we show that
has nonempty values. Now, we show that  is closed. Indeed, if
is closed. Indeed, if  , then there exists a net
, then there exists a net  in
in  such that
such that  . Since
. Since

there exist  and
and  such that
such that  . Let
. Let

Then  is a compact subset of
is a compact subset of  ,
,  and
and  are compact subsets of
are compact subsets of  . By condition (iii)2 and Lemma 2.2(iii),
. By condition (iii)2 and Lemma 2.2(iii),  is a compact subset of
is a compact subset of  . Thus, we can assume that
. Thus, we can assume that  . By condition (iii)2,
. By condition (iii)2,  is closed, and hence
is closed, and hence  . Since
. Since  and
and  is closed, we have
is closed, we have  . Letting
. Letting  , it follows that
, it follows that

and so  is closed.
is closed.
By the above discussions, we know that condition (iii) of Theorem 3.1 is satisfied. It is easy to check that condition (iv) of Theorem 3.1 is also satisfied. By Theorem 3.1, there exists  with
with  and
and  such that for each
such that for each  ,
,  ,
,  and
and

for all  . This completes the proof.
. This completes the proof.
For the special case of Theorem 3.3, we have the following corollary which is actually an existence theorem of solutions for variational equations.
Corollary 3.4.
For each  , suppose that conditions (i) and (ii) in Theorem 3.1 hold. Moreover,
, suppose that conditions (i) and (ii) in Theorem 3.1 hold. Moreover,
(iii)3 is a continuous map and
is a continuous map and  is a continuous map;
is a continuous map;
(iv)3 for each  ,
,  is
is  -quasiconvex; for each
-quasiconvex; for each  ,
,  is also
is also  -quasiconvex and
-quasiconvex and  .
.
Then, there exists  with
with  and
and  such that for each
such that for each  ,
,  ,
,  and
and  for all
for all  .
.
From Theorem 3.3, we establish the following corollary which is actually an existence theorem of solutions for systems of generalized vector quasiequilibrium problems.
Corollary 3.5.
For each  , suppose that conditions (i) and (ii) in Theorem 3.1 hold. Moreover,
, suppose that conditions (i) and (ii) in Theorem 3.1 hold. Moreover,
(iii)4 is a closed map with nonempty values and
is a closed map with nonempty values and  is an u.s.c. map with nonempty compact values;
is an u.s.c. map with nonempty compact values;
(iv)4for each  ,
,  is
is  -quasiconvex; for each
-quasiconvex; for each  ,
,  is
is  -quasiconvex-like and
-quasiconvex-like and  .
.
Then, there exists  with
with  and
and  such that for each
such that for each  ,
,  ,
,  , and
, and  for all
for all  .
.
Proof.
Define  by
by  for all
for all  . Since
. Since  is a closed map with nonempty values, we have that
is a closed map with nonempty values, we have that  is a closed map with nonempty values. All the conditions of Theorem 3.3 are satisfied. The conclusion of Corollary 3.5 follows from Theorem 3.3. This completes the proof.
is a closed map with nonempty values. All the conditions of Theorem 3.3 are satisfied. The conclusion of Corollary 3.5 follows from Theorem 3.3. This completes the proof.
4. Applications to Optimization Problems
Let  be a real topological vector space,
be a real topological vector space,  a proper convex cone in
a proper convex cone in  . A point
. A point  is called a vector minimal point of
is called a vector minimal point of  if for any
if for any  ,
,  . The set of vector minimal point of
. The set of vector minimal point of  is denoted by
is denoted by  .
.
Lemma 4.1 . (see [27]).
Let  be a Hausdorff t.v.s.,
be a Hausdorff t.v.s.,  be a closed convex cone in
be a closed convex cone in  . If
. If  is a nonempty compact subset of
is a nonempty compact subset of  , then
, then  .
.
Theorem 4.2.
For each  , suppose that conditions (i), (ii) in Theorem 3.1 and conditions (iii)
, suppose that conditions (i), (ii) in Theorem 3.1 and conditions (iii) , (iv)
, (iv) in Corollary 3.5 hold. Furthermore, let
in Corollary 3.5 hold. Furthermore, let  be an u.s.c. map with nonempty compact values, where
be an u.s.c. map with nonempty compact values, where  is a real t.v.s. ordered by a proper closed convex cone in
is a real t.v.s. ordered by a proper closed convex cone in  . Then, there exists a solution to:
. Then, there exists a solution to:

where  and
and  such that for each
such that for each  ,
,  ,
,  , and
, and  for all
for all  .
.
Proof.
By Corollary 3.5, there exists  with
with  and
and  such that for each
such that for each  ,
,  ,
,  and
and  for all
for all  . For each
. For each  , let
, let

and  . Then
. Then  and
and  . We show that
. We show that  is closed for each
is closed for each  . Indeed, if
. Indeed, if  , then there exists a net
, then there exists a net  in
in  such that
such that  . For each
. For each  ,
,  implies that
implies that

By the closedness of  and
and  , we have that
, we have that  and
and  . Now, we prove that
. Now, we prove that  for all
for all  . For any
. For any  , since
, since  is l.s.c., there exists a net
is l.s.c., there exists a net  satisfying
satisfying  and
and  . Let
. Let  . Since
. Since  is u.s.c. with nonempty compact values, we can assume that
is u.s.c. with nonempty compact values, we can assume that  . By the closedness of
. By the closedness of  and
and  , we have that
, we have that  . Thus,
. Thus,  . It follows that
. It follows that  is closed. Hence,
is closed. Hence,  is closed. Note that
is closed. Note that  . We know that
. We know that  is a nonempty compact subset of
is a nonempty compact subset of  . It follows from Lemma 2.2(iii) that
. It follows from Lemma 2.2(iii) that  is a nonempty compact subset of
is a nonempty compact subset of  . By Lemma 4.1,
. By Lemma 4.1,  . That is there exists a solution of the problem:
. That is there exists a solution of the problem:  where
where  . This completes the proof.
. This completes the proof.
Theorem 4.3.
For each  , suppose that
, suppose that  is compact and condition (ii) in Theorem 3.1 holds. Moreover,
is compact and condition (ii) in Theorem 3.1 holds. Moreover,
(iii)5 is a continuous function;
is a continuous function;
(iv)5 for each  ,
,  is
is  -quasiconvex; for each
-quasiconvex; for each  ,
,  is also
is also  -quasiconvex and
-quasiconvex and  .
.
Furthermore, let  is a l.s.c. function. Then there exists a solution to:
is a l.s.c. function. Then there exists a solution to:

where  and
and  such that for each
such that for each  ,
,  and
and  for all
for all  .
.
Proof.
For each  , define
, define  and
and  by
by

respectively. It is easy to check that all the conditions of Corollary 3.5 are satisfied. For each  , define
, define

and  . Then, by Corollary 3.5, there exists
. Then, by Corollary 3.5, there exists  and hence
and hence  . Arguing as Theorem 4.2, we can prove that
. Arguing as Theorem 4.2, we can prove that  is a nonempty compact subset of
is a nonempty compact subset of  . Hence there exists a solution to the problem
. Hence there exists a solution to the problem  where
where  . This completes the proof.
. This completes the proof.
Remark 4.4.
Theorem 4.3 generalizes [28, Corollary 3.5] from locally convex topological vector spaces to  -spaces.
-spaces.
Theorem 4.5.
For each  , suppose that
, suppose that  is compact and condition (ii) in Theorem 3.1 holds. Moreover,
is compact and condition (ii) in Theorem 3.1 holds. Moreover,
(iii)6 is a continuous function;
is a continuous function;
(iv)6 for each  ,
,  is
is  -quasiconvex.
-quasiconvex.
Furthermore, let  be a l.s.c. function. Then, there exists a solution to the problem:
be a l.s.c. function. Then, there exists a solution to the problem:

where  and
and  such that for each
such that for each  ,
,  is the solution of the problem
is the solution of the problem  .
.
Proof.
For each  , define
, define  by
by

It is easy to check that all the conditions of Theorem 4.3 are satisfied. Theorem 4.5 follows immediately from Theorem 4.3. This completes the proof.
References
Robinson SM: Generalized equations and their solutions. I. Basic theory. Mathematical Programming Study 1979, 10: 128–141. 10.1007/BFb0120850
Chang SS: Set-valued variational inclusions in Banach spaces. Journal of Mathematical Analysis and Applications 2000,248(2):438–454. 10.1006/jmaa.2000.6919
Ding XP: Perturbed proximal point algorithms for generalized quasivariational inclusions. Journal of Mathematical Analysis and Applications 1997,210(1):88–101. 10.1006/jmaa.1997.5370
Huang N-J: A new class of generalized set-valued implicit variational inclusions in Banach spaces with an application. Computers & Mathematics with Applications 2001,41(7–8):937–943. 10.1016/S0898-1221(00)00331-X
Lin L-J: Systems of generalized quasivariational inclusions problems with applications to variational analysis and optimization problems. Journal of Global Optimization 2007,38(1):21–39. 10.1007/s10898-006-9081-5
Lin L-J: Variational inclusions problems with applications to Ekeland's variational principle, fixed point and optimization problems. Journal of Global Optimization 2007,39(4):509–527. 10.1007/s10898-007-9153-1
Lin L-J: Systems of variational inclusion problems and differential inclusion problems with applications. Journal of Global Optimization 2009,44(4):579–591. 10.1007/s10898-008-9359-x
Tarafdar E: Fixed point theorems in locally -convex uniform spaces. Nonlinear Analysis 1997,29(9):971–978. 10.1016/S0362-546X(96)00174-5
Himmelberg CJ: Fixed points of compact multifunctions. Journal of Mathematical Analysis and Applications 1972, 38: 205–207. 10.1016/0022-247X(72)90128-X
Park S: Fixed point theorems in locally -convex spaces. Nonlinear Analysis 2002,48(6):869–879. 10.1016/S0362-546X(00)00220-0
Park S: On generalizations of the KKM principle on abstract convex spaces. Nonlinear Analysis Forum 2006,11(1):67–77.
Park S: Fixed point theory of multimaps in abstract convex uniform spaces. Nonlinear Analysis 2009,71(7–8):2468–2480. 10.1016/j.na.2009.01.081
Deng L, Yang MG: Coincidence theorems with applications to minimax inequalities, section theorem, best approximation and multiobjective games in topological spaces. Acta Mathematica Sinica (English Series) 2006,22(6):1809–1818. 10.1007/s10114-005-0743-x
Deng L, Yang MG: Weakly R-KKM mappings-intersection theorems and minimax inequalities in topological spaces. Applied Mathematics and Mechanics 2007,28(1):103–109. 10.1007/s10483-007-0112-1
Park S: Several episodes in recent studies on the KKM theory. Nonlinear Analysis Forum 2010, 15: 13–26.
Park S: Generalized convex spaces, -spaces, and -spaces. Journal of Global Optimization 2009,45(2):203–210. 10.1007/s10898-008-9363-1
Park S: Remarks on fixed points, maximal elements, and equilibria of economies in abstract convex spaces. Taiwanese Journal of Mathematics 2008,12(6):1365–1383.
Park S: Remarks on the partial KKM principle. Nonlinear Analysis Forum 20009, 14: 51–62.
Park S: Comments on recent studies on abstract convex spaces. Nonlinear Analysis Forum 2008, 13: 1–17.
Park S: The rise and decline of generalized convex spaces. Nonlinear Analysis Forum 2010, 15: 1–12.
Yang M-G, Xu J-P, Huang N-J, Yu S-J: Minimax theorems for vector-valued mappings in abstract convex spaces. Taiwanese Journal of Mathematics 2010,14(2):719–732.
Tan NX: Quasi-variational inequalities in topological linear locally convex Hausdorff spaces. Mathematische Nachrichten 1985, 122: 231–224. 10.1002/mana.19851220123
Aubin JP, Cellina A: Differential Inclusion. Springer, Berlin, Germany; 1994.
Park S: Equilibrium existence theorems in KKM spaces. Nonlinear Analysis 2008,69(12):4352–5364. 10.1016/j.na.2007.10.058
Kelley JL: General Topology. Volume 2. Springer, New York, NY, USA; 1975:xiv+298.
Ding XP: The generalized game and the system of generalized vector quasi-equilibrium problems in locally -uniform spaces. Nonlinear Analysis 2008,68(4):1028–1036. 10.1016/j.na.2006.12.003
Luc DC: Theory of Vector Optimization, Lecture Notes in Economics and Mathematical Systems. Volume 319. Springer, Berlin, Germany; 1989:viii+173.
Lin L-J: Mathematical programming with system of equilibrium constraints. Journal of Global Optimization 2007,37(2):275–286. 10.1007/s10898-006-9049-5
Acknowledgments
This work was supported by the Key Program of NSFC (Grant no. 70831005) and the Open Fund (PLN0904) of State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation (Southwest Petroleum University).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yang, Mg., Xu, Jp. & Huang, Nj. Systems of Generalized Quasivariational Inclusion Problems with Applications in  -Spaces.
Fixed Point Theory Appl 2011, 561573 (2011). https://doi.org/10.1155/2011/561573
-Spaces.
Fixed Point Theory Appl 2011, 561573 (2011). https://doi.org/10.1155/2011/561573
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/561573
 is a compact space and
is a compact space and 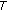 is closed, then
is closed, then 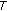 is u.s.c.
is u.s.c. is compact and
is compact and 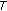 is an u.s.c. map with compact values, then
is an u.s.c. map with compact values, then 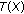 is compact.
is compact.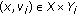 ,
, 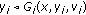 is
is  -quasiconvex; for each
-quasiconvex; for each 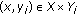 ,
, 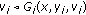 is
is  -quasiconvex-like and
-quasiconvex-like and  .
.