- Research Article
- Open access
- Published:
Strong Convergence Theorems for Lipschitzian Demicontraction Semigroups in Banach Spaces
Fixed Point Theory and Applications volume 2011, Article number: 583423 (2011)
Abstract
The purpose of this paper is to introduce and study the strong convergence problem of the explicit iteration process for a Lipschitzian and demicontraction semigroups in arbitrary Banach spaces. The main results presented in this paper not only extend and improve some recent results announced by many authors, but also give an affirmative answer for the open questions raised by Suzuki (2003) and Xu (2005).
1. Introduction and Preliminaries
Throughout this paper, we assume that  is a real Banach space,
is a real Banach space,  is the dual space of
is the dual space of  ,
,  is a nonempty closed convex subset of
is a nonempty closed convex subset of  ,
,  is the set of nonnegative real numbers, and
is the set of nonnegative real numbers, and  is the normalized duality mapping defined by
is the normalized duality mapping defined by

for all  . Let
. Let  be a mapping. We use
be a mapping. We use  to denote the set of fixed points of
to denote the set of fixed points of  . We also use "
. We also use " " to stand for strong convergence and "
" to stand for strong convergence and " " for weak convergence.
" for weak convergence.
Definition 1.1.
-
(1)
The one-parameter family
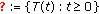 of mappings from
of mappings from 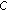 into itself is called a nonexpansive semigroup if the following conditions are satisfied:
into itself is called a nonexpansive semigroup if the following conditions are satisfied:
(a) for each
for each  ;
;
(b) for any
for any  and
and  ;
;
-
(c)
for any
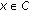 , the mapping
, the mapping 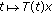 is continuous;
is continuous; -
(d)
for any
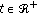 ,
, 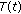 is a nonexpansive mapping on
is a nonexpansive mapping on 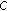 , that is, for any
, that is, for any 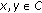 ,
,

for any  .
.
-
(2)
The one-parameter family
 of mappings from
of mappings from 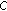 into itself is called a pseudocontraction semigroup if the conditions (a)–(c) and the following condition (e) are satisfied:
into itself is called a pseudocontraction semigroup if the conditions (a)–(c) and the following condition (e) are satisfied: -
(e)
for any
 , there exists
, there exists  such that
such that 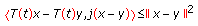 (1.3)
(1.3)
for any  .
.
-
(3)
A pseudocontraction semigroup
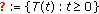 of mappings from
of mappings from  into itself is said to be Lipschitzian if the conditions (a)–(c), (e), and the following condition (f) are satisfied:
into itself is said to be Lipschitzian if the conditions (a)–(c), (e), and the following condition (f) are satisfied: -
(f)
there exists a bounded measurable function
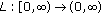 such that, for any
such that, for any 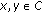 ,
,  (1.4)
(1.4)
for any  . In the sequel, we denote it by
. In the sequel, we denote it by

From the definitions, it is easy to see that every nonexpansive semigroup is a Lipschitzian and pseudocontraction semigroup with  .
.
-
(4)
The one-parameter family
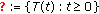 of mappings from
of mappings from  into itself is called a strictly pseudocontractive semigroup if the conditions (a)–(c) and the following condition (g) are satisfied:
into itself is called a strictly pseudocontractive semigroup if the conditions (a)–(c) and the following condition (g) are satisfied: -
(g)
there exists a bounded function
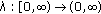 such that, for any given
such that, for any given  , there exists
, there exists 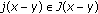 such that
such that 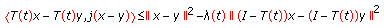 (1.6)
(1.6)
for any  .
.
It is easy to see that such mapping is  -Lipschitzian and pseudocontractive semigroup.
-Lipschitzian and pseudocontractive semigroup.
-
(5)
The one-parameter family
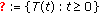 of mappings from
of mappings from 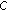 into itself is called a demicontractive semigroup if
into itself is called a demicontractive semigroup if 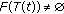 for all
for all  and the conditions (a)–(c) and the following condition (h) are satisfied:
and the conditions (a)–(c) and the following condition (h) are satisfied: -
(h)
there exists a bounded function
 such that, for any
such that, for any 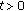 ,
, 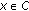 and
and 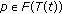 , there exists
, there exists  such that
such that  (1.7)
(1.7)
In this case, we also say that  is a
is a  -demicontractive semigroup.
-demicontractive semigroup.
Remark 1.2.
-
(1)
It is easy to see that the condition (1.7) is equivalent to the following condition: for any
 ,
, 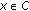 and
and  ,
, 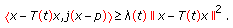 (1.8)
(1.8)
-
(2)
Every strictly pseudocontractive semigroup with
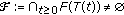 is demi-contractive and Lipschitzian.
is demi-contractive and Lipschitzian.
The convergence problems of the implicit or explicit iterative sequences for nonexpansive semigroup to a common fixed has been considered by some authors in the settings of Hilbert or Banach spaces (see, e.g., [1–10]).
In 1998, Shioji and Takahashi [7] introduced the following implicit iteration:

for each  in a Hilbert space, where
in a Hilbert space, where  is a sequence in
is a sequence in  ,
,  is a sequence of positive real numbers divergent to
is a sequence of positive real numbers divergent to  , and, for any
, and, for any  and
and  ,
,  is the average given by
is the average given by

Under certain restrictions to the sequence  , they proved some strong convergence theorems of
, they proved some strong convergence theorems of  to a point
to a point  .
.
In 2003, Suzuki [8] first introduced the following implicit iteration process for the nonexpansive semigroup in a Hilbert space:

for each  . Under appropriate assumptions imposed upon the sequences
. Under appropriate assumptions imposed upon the sequences  and
and  , he proved that the sequence
, he proved that the sequence  defined by (1.11) converges strongly to a common fixed point of the nonexpansive semigroup. At the same time, he also raised the following open question.
defined by (1.11) converges strongly to a common fixed point of the nonexpansive semigroup. At the same time, he also raised the following open question.
Open Question 1.3 (see [8]).
Does there exist an explicit iteration concerning Suzuki's result? That is, for any given  , if we define an explicit iterative sequence
, if we define an explicit iterative sequence  by
by

for each  , what conditions to be imposed on
, what conditions to be imposed on  and
and  are sufficient to guarantee the strong convergence of
are sufficient to guarantee the strong convergence of  to a common fixed point of the nonexpansive semi-group
to a common fixed point of the nonexpansive semi-group  of mapping from
of mapping from  into itself?
into itself?
In 2005, Xu [9] proved that Suzuki's result holds in a uniformly convex Banach space with a weakly continuous duality mapping. At the same time, he also raised the following open question.
Open Question 1.4 (see [9]).
We do not know whether or not the same result holds in a uniformly convex and uniformly smooth Banach space.
In 2005, Aleyner and Reich [1] first introduced the following explicit iteration sequence:

for each  in a reflexive Banach space with a uniformly Gâteaux differentiable norm such that each nonempty bounded closed and convex subset of
in a reflexive Banach space with a uniformly Gâteaux differentiable norm such that each nonempty bounded closed and convex subset of  has the common fixed point property for nonexpansive mappings (note that all these assumptions are fulfilled whenever
has the common fixed point property for nonexpansive mappings (note that all these assumptions are fulfilled whenever  is uniformly smooth [11]).
is uniformly smooth [11]).
Also, under appropriate assumptions imposed upon the parameter sequences  and
and  , they proved that the sequence
, they proved that the sequence  defined by (1.13) converges strongly to some point in
defined by (1.13) converges strongly to some point in  .
.
Recently, in 2007, Zhang et al. [3] introduced the following composite iteration scheme in the framework of reflexive Banach with a uniformly Gâteaux differentiable norm, uniformly smooth Banach space and uniformly convex Banach space with a weakly continuous normalized duality mapping:

for each  for the nonexpansive semi-group
for the nonexpansive semi-group  of mappings from
of mappings from  into itself, where
into itself, where  is an arbitrary (but fixed) element in
is an arbitrary (but fixed) element in  and the sequences
and the sequences  in
in  ,
,  in
in  ,
,  in
in  , and proved some strong convergence theorems for the iteration sequence
, and proved some strong convergence theorems for the iteration sequence  . In fact, the results presented in [3] not only extend and improve the corresponding results of Shioji and Takahashi [7], Suzuki [8], Xu [9], and Aleyner and Reich [1], but also give a partially affirmative answer for the open questions raised by Suzuki [8] and Xu [9].
. In fact, the results presented in [3] not only extend and improve the corresponding results of Shioji and Takahashi [7], Suzuki [8], Xu [9], and Aleyner and Reich [1], but also give a partially affirmative answer for the open questions raised by Suzuki [8] and Xu [9].
In order to improve and develop the results mentioned above, recently, Zhang [12, 13], by using the different methods, introduce and study the weak convergence problem of the implicit iteration processes for the Lipschitzian and pseudocontraction semigroups in general Banach spaces. The results given in [12, 13] not only extend the above results, but also extend and improve the corresponding results in Li et al. [6], Osilike [14], Xu and Ori [15], and Zhou [16].
The purpose of this paper is to introduce and study the strong convergence problem of the following explicit iteration process:

for each  for the Lipschitzian and demicontractive semigroup
for the Lipschitzian and demicontractive semigroup  in general Banach spaces. The results presented in this paper improve, extend, and replenish the corresponding results given in [1, 3–10, 12, 13].
in general Banach spaces. The results presented in this paper improve, extend, and replenish the corresponding results given in [1, 3–10, 12, 13].
In the sequel, we make use of the following lemmas for our main results.
Lemma 1.5.
Let  be the normalized duality mapping. Then, for any
be the normalized duality mapping. Then, for any  ,
,

for all  .
.
Lemma 1.6 (see [17]).
Let  and
and  be the sequences of nonnegative real numbers satisfying the following condition:
be the sequences of nonnegative real numbers satisfying the following condition:

for all  , where
, where  is some nonnegative integer. If
is some nonnegative integer. If  , then the limit
, then the limit  exists. In addition, if there exists a subsequence
exists. In addition, if there exists a subsequence  of
of  such that
such that  , then
, then  .
.
2. Main Results
Now, we are ready to give our main results in this paper.
Theorem 2.1.
Let  be a real Banach space; let
be a real Banach space; let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and let
, and let  be a Lipschitzian and demicontractive semigroup with a bounded measurable function
be a Lipschitzian and demicontractive semigroup with a bounded measurable function  and a bounded function
and a bounded function  , respectively, such that
, respectively, such that

Let  be the sequence defined by (1.15), where
be the sequence defined by (1.15), where  is a sequence in
is a sequence in  and
and  is an increasing sequence in
is an increasing sequence in  . If the following conditions are satisfied:
. If the following conditions are satisfied:
(a) ,
,  ;
;
-
(b)
for any bounded subset
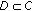 ,
,

then we have the following:
(1) exists for all
exists for all  .
.
(2) .
.
Proof.
-
(1)
For any
 , we have
, we have 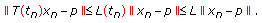 (2.3)
(2.3)
It follows from (2.3) that

Consequently, it follows from (2.3) and (2.4) that


From (2.5), we have

Since  is an demicontractive semigroup with
is an demicontractive semigroup with  , for the points
, for the points  and
and  , there exists
, there exists  such that
such that

Thus, by Lemma 1.5, (2.4), (2.7), and (2.8), we have

This implies that

By the assumption  , it follows from Lemma 1.6 that the limit
, it follows from Lemma 1.6 that the limit  exists and so the sequence
exists and so the sequence  is bounded in
is bounded in  .
.
-
(2)
We first prove that
 (2.11)
(2.11)
If it is not the case, suppose  . There exists a positive integer
. There exists a positive integer  such that
such that

for each  . Since
. Since  is bounded, denote by
is bounded, denote by

Thus it follows from (2.9) that

for each  . This implies that
. This implies that

for each  . Hence, for each
. Hence, for each  , we have
, we have

Letting  in (2.16), we have
in (2.16), we have

which is a contradiction since, by the condition (a),  and
and  . Therefore, the conclusion (2.11) is proved.
. Therefore, the conclusion (2.11) is proved.
On the other hand, since  is bounded and
is bounded and  is increasing, it follows from (2.11) and the condition (b) that
is increasing, it follows from (2.11) and the condition (b) that

This completes the proof.
By using Theorem 2.1, we have the following.
Theorem 2.2.
Let  be a real Banach space; let
be a real Banach space; let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and let
, and let  of mappings from
of mappings from  into itself be a Lipschitzian and demicontractive semigroup with a bounded measurable function
into itself be a Lipschitzian and demicontractive semigroup with a bounded measurable function  and a bounded function
and a bounded function  , respectively, such that
, respectively, such that

Let  be the sequence defined by (1.15), where
be the sequence defined by (1.15), where  is a sequence in
is a sequence in  and
and  is an increasing sequence in
is an increasing sequence in  . If there exists a compact subset
. If there exists a compact subset  of
of  such that
such that  and the following conditions are satisfied:
and the following conditions are satisfied:
(a) ,
,  ;
;
-
(b)
for any bounded subset
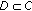 ,
,

then  converges strongly to a common fixed point of the semigroup
converges strongly to a common fixed point of the semigroup  .
.
Proof.
By Theorem 2.1, we have  . Again, by the assumption, it follows that there exists a compact subset
. Again, by the assumption, it follows that there exists a compact subset  such that
such that  and so there exists a subsequence
and so there exists a subsequence  of
of  such that
such that

for some point  . Hence it follows from (2.21) that
. Hence it follows from (2.21) that  as
as  .
.
Next, we prove that

for all  . In fact, it follows from the condition (b) and (2.21) that, for any
. In fact, it follows from the condition (b) and (2.21) that, for any  ,
,

as  . Since
. Since  as
as  and the semigroup
and the semigroup  is Lipschitzian, it follows from (2.23) that
is Lipschitzian, it follows from (2.23) that  for all
for all  , that is,
, that is,

Since  as
as  and the limit
and the limit  exists by Theorem 2.1 (1), which implies that
exists by Theorem 2.1 (1), which implies that  as
as  . This completes the proof.
. This completes the proof.
Remark 2.3.
Theorem 2.2 not only extends and improves the corresponding results of Shioji and Takahashi [7], Suzuki [8], Xu [9], and Aleyner and Reich [1], but also gives an affirmative answer to the open questions raised by Suzuki [8] and Xu [9].
References
Aleyner A, Reich S: An explicit construction of sunny nonexpansive retractions in Banach spaces. Fixed Point Theory and Applications 2005, (3):295–305.
Boonchari D, Saejung S: Construction of common fixed points of a countable family of -demicontractive mappings in arbitrary Banach spaces. Applied Mathematics and Computation 2010,216(1):173–178. 10.1016/j.amc.2010.01.027
Zhang S-S, Yang L, L.u J-A: Strong convergence theorems for nonexpansive semi-groups in Banach spaces. Applied Mathematics and Mechanics 2007,28(10):1287–1297. 10.1007/s10483-007-1002-x
Chang SS, Chan CK, Joseph Lee HW, Yang L: A system of mixed equilibrium problems, fixed point problems of strictly pseudo-contractive mappings and nonexpansive semi-groups. Applied Mathematics and Computation 2010,216(1):51–60. 10.1016/j.amc.2009.12.060
Chen R, Song Y, Zhou H: Convergence theorems for implicit iteration process for a finite family of continuous pseudocontractive mappings. Journal of Mathematical Analysis and Applications 2006,314(2):701–709. 10.1016/j.jmaa.2005.04.018
Li S, Li LH, Su F: General iterative methods for a one-parameter nonexpansive semigroup in Hilbert space. Nonlinear Analysis: Theory, Methods & Applications 2009,70(9):3065–3071. 10.1016/j.na.2008.04.007
Shioji N, Takahashi W: Strong convergence theorems for asymptotically nonexpansive semigroups in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 1998,34(1):87–99. 10.1016/S0362-546X(97)00682-2
Suzuki T: On strong convergence to common fixed points of nonexpansive semigroups in Hilbert spaces. Proceedings of the American Mathematical Society 2003,131(7):2133–2136. 10.1090/S0002-9939-02-06844-2
Xu H-K: A strong convergence theorem for contraction semigroups in Banach spaces. Bulletin of the Australian Mathematical Society 2005,72(3):371–379. 10.1017/S000497270003519X
Zhang SS, Yang L, Lee HWJ, Chan CK: Strong convergence theorems for nonexpansive semigroups in Hilbert spaces. Acta Mathematica Sinica 2009,52(2):337–342.
Browder FE: Nonlinear operators and nonlinear equations of evolution in Banach spaces. In Nonlinear Functional Analysis (Proc. Sympos. Pure Math., Vol. XVIII, Part 2, Chicago, Ill., 1968). American Mathematical Society, Providence, RI, USA; 1976:1–308.
Zhang S-S: Convergence theorem of common fixed points for Lipschitzian pseudo-contraction semi-groups in Banach spaces. Applied Mathematics and Mechanics 2009,30(2):145–152. 10.1007/s10483-009-0202-y
Zhang SS: Weak convergence theorem for Lipschizian pseudocontraction semigroups in Banach spaces. Acta Mathematica Sinica 2010,26(2):337–344. 10.1007/s10114-010-7610-0
Osilike MO: Implicit iteration process for common fixed points of a finite family of strictly pseudocontractive maps. Journal of Mathematical Analysis and Applications 2004,294(1):73–81. 10.1016/j.jmaa.2004.01.038
Xu H-K, Ori RG: An implicit iteration process for nonexpansive mappings. Numerical Functional Analysis and Optimization 2001,22(5–6):767–773. 10.1081/NFA-100105317
Zhou H: Convergence theorems of common fixed points for a finite family of Lipschitz pseudocontractions in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,68(10):2977–2983. 10.1016/j.na.2007.02.041
Xu HK: Inequalities in Banach spaces with applications. Nonlinear Analysis: Theory, Methods & Applications 1991,16(12):1127–1138. 10.1016/0362-546X(91)90200-K
Acknowledgment
The first author was supported by the Natural Science Foundation of Yibin University (No. 2009Z3), and the second author was supported by the Korea Research Foundation Grant funded by the Korean Government (KRF-2008-313-C00050).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chang, Ss., Cho, Y., Lee, H. et al. Strong Convergence Theorems for Lipschitzian Demicontraction Semigroups in Banach Spaces. Fixed Point Theory Appl 2011, 583423 (2011). https://doi.org/10.1155/2011/583423
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/583423
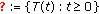 of mappings from
of mappings from 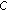 into itself is called a nonexpansive semigroup if the following conditions are satisfied:
into itself is called a nonexpansive semigroup if the following conditions are satisfied: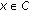 , the mapping
, the mapping 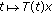 is continuous;
is continuous;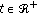 ,
, 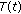 is a nonexpansive mapping on
is a nonexpansive mapping on 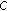 , that is, for any
, that is, for any 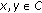 ,
, of mappings from
of mappings from 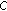 into itself is called a pseudocontraction semigroup if the conditions (a)–(c) and the following condition (e) are satisfied:
into itself is called a pseudocontraction semigroup if the conditions (a)–(c) and the following condition (e) are satisfied: , there exists
, there exists  such that
such that 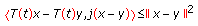
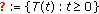 of mappings from
of mappings from  into itself is said to be Lipschitzian if the conditions (a)–(c), (e), and the following condition (f) are satisfied:
into itself is said to be Lipschitzian if the conditions (a)–(c), (e), and the following condition (f) are satisfied: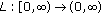 such that, for any
such that, for any 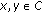 ,
, 
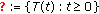 of mappings from
of mappings from  into itself is called a strictly pseudocontractive semigroup if the conditions (a)–(c) and the following condition (g) are satisfied:
into itself is called a strictly pseudocontractive semigroup if the conditions (a)–(c) and the following condition (g) are satisfied: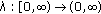 such that, for any given
such that, for any given  , there exists
, there exists 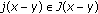 such that
such that 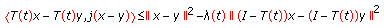
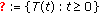 of mappings from
of mappings from 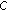 into itself is called a demicontractive semigroup if
into itself is called a demicontractive semigroup if 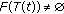 for all
for all  and the conditions (a)–(c) and the following condition (h) are satisfied:
and the conditions (a)–(c) and the following condition (h) are satisfied: such that, for any
such that, for any 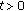 ,
, 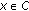 and
and 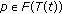 , there exists
, there exists  such that
such that 
 ,
, 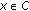 and
and  ,
, 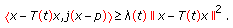
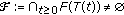 is demi-contractive and Lipschitzian.
is demi-contractive and Lipschitzian.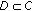 ,
, , we have
, we have 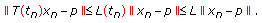

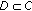 ,
,