- Research Article
- Open access
- Published:
Existence Result of Generalized Vector Quasiequilibrium Problems in Locally 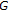 -Convex Spaces
-Convex Spaces
Fixed Point Theory and Applications volume 2011, Article number: 967515 (2011)
Abstract
This paper deals with the generalized strong vector quasiequilibrium problems without convexity in locally  -convex spaces. Using the Kakutani-Fan-Glicksberg fixed point theorem for upper semicontinuous set-valued mapping with nonempty closed acyclic values, the existence theorems for them are established. Moreover, we also discuss the closedness of strong solution set for the generalized strong vector quasiequilibrium problems.
-convex spaces. Using the Kakutani-Fan-Glicksberg fixed point theorem for upper semicontinuous set-valued mapping with nonempty closed acyclic values, the existence theorems for them are established. Moreover, we also discuss the closedness of strong solution set for the generalized strong vector quasiequilibrium problems.
1. Introduction
Let  be real topological vector space, and let
be real topological vector space, and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a bifunction, where
be a bifunction, where  is the set of real numbers. The equilibrium problem for
is the set of real numbers. The equilibrium problem for  is to find
is to find  such that
such that

Problem (1.1) was studied by Blum and Oettli [1]. The set of solution of (1.1) is denoted by  . The equilibrium problem contains many important problems as special cases, including optimization, Nash equilibrium, complementarity, and fixed point problems (see [1–3] and the references therein). Recently, there has been an increasing interest in the study of vector equilibrium problems. Many results on the existence of solutions for vector variational inequalities and vector equilibrium problems have been established (see, e.g., [4–16]).
. The equilibrium problem contains many important problems as special cases, including optimization, Nash equilibrium, complementarity, and fixed point problems (see [1–3] and the references therein). Recently, there has been an increasing interest in the study of vector equilibrium problems. Many results on the existence of solutions for vector variational inequalities and vector equilibrium problems have been established (see, e.g., [4–16]).
Let  and
and  be real topological vector spaces and
be real topological vector spaces and  a nonempty subset of
a nonempty subset of  . Let
. Let  be a closed and convex cone in
be a closed and convex cone in  with
with  , where
, where  denotes the topological interior of
denotes the topological interior of  . For a bifunction
. For a bifunction  , the vector equilibrium problem (for short, VEP) is to find
, the vector equilibrium problem (for short, VEP) is to find  such that
such that

which is a unified model of several known problems, for instance, vector variational and variational-like inequality problems, vector complementarity problem, vector optimization problem, and vector saddle point problem; see, for example, [3, 8, 17, 18] and references therein. In 2003, Ansari and Yao [19] introduced vector quasiequilibrium problem (for short, VQEP) to find  such that
such that

where  is a multivalued map with nonempty values.
is a multivalued map with nonempty values.
Recently, Ansari et al. [4] considered a more general problem which contains VEP and generalized vector variational inequality problems as special cases. Let  and
and  be real locally convex Hausdorff space,
be real locally convex Hausdorff space,  a nonempty subset and
a nonempty subset and  a closed convex pointed cone. Let
a closed convex pointed cone. Let  be a given set-valued mapping. Ansari et al. [4] introduced the following problems, to find
be a given set-valued mapping. Ansari et al. [4] introduced the following problems, to find  such that
such that

or to find  such that
such that

It is called generalized vector equilibrium problem (for short, GVEP), and it has been studied by many authors; see, for example, [20–22] and references therein. For other possible ways to generalize VEP, we refer to [23–25]. If  is nonempty and
is nonempty and  satisfies (1.4), then we call
satisfies (1.4), then we call  a weak efficient solution for VEP, and if
a weak efficient solution for VEP, and if  satisfies (1.5), then we call
satisfies (1.5), then we call  a strong solution for VEP. Moreover, they also proved an existence theorem for a strong vector equilibrium problem (1.5) (see [4]).
a strong solution for VEP. Moreover, they also proved an existence theorem for a strong vector equilibrium problem (1.5) (see [4]).
On the other hand, it is well known that a strong solution of vector equilibrium problem is an ideal solution; it is better than other solutions such as efficient solution, weak efficient solution, proper efficient solution, and supper efficient solution (see [12]). Thus, it is important to study the existence of strong solution and properties of the strong solution set. In 2003, Ansari and Flores-Bazán [26] considered the following generalized vector quasiequilibrium problem (for short, GVQEP): to find  such that
such that

Very recently, the generalized strong vector quasiequilibrium problem (in short, GSVQEP) is introduced by Hou et al. [27] and Long et al. [16]. Let  , and
, and  be real locally convex Hausdorff topological vector spaces,
be real locally convex Hausdorff topological vector spaces,  and
and  nonempty compact convex subsets, and
nonempty compact convex subsets, and  a nonempty closed convex cone. Let
a nonempty closed convex cone. Let  ,
,  and
and  be three set-valued mappings. They considered the GSVQEP, finding
be three set-valued mappings. They considered the GSVQEP, finding  such that
such that  and
and

Moreover, they gave an existence theorem for a generalized strong vector quasiequilibrium problem without assuming that the dual of the ordering cone has a weak compact base.
compact base.
Throughout this paper, motivated and inspired by Hou et al. [27], Long et al. [16], and Yuan [28], we will introduce and study the generalized vector quasiequilibrium problem on locally  -convex Hausdorff topological vector spaces. Let
-convex Hausdorff topological vector spaces. Let  ,
,  , and
, and  be real locally
be real locally  -convex Hausdorff topological vector spaces,
-convex Hausdorff topological vector spaces,  and
and  nonempty compact subsets, and
nonempty compact subsets, and  a nonempty closed convex cone. We also suppose that
a nonempty closed convex cone. We also suppose that  ,
,  and
and  are set-valued mappings.
are set-valued mappings.
The generalized vector quasiequilibrium problem of type (I) (GSVQEP I) is to find  such that
such that

The generalized vector quasiequilibrium problem of type (II) (GSVQEP II) is to find  such that
such that

We denote the set of all solution to the (GSVQEP I) and (GSVQEP II) by  and
and  , respectively. The main motivation of this paper is to prove the existence theorems of the generalized strong vector quasiequilibrium problems in locally
, respectively. The main motivation of this paper is to prove the existence theorems of the generalized strong vector quasiequilibrium problems in locally  -convex spaces, by using Kakutani-Fan-Glicksberg fixed point theorem for upper semicontinuous set-valued mapping with nonempty closed acyclic values, and the closedness of
-convex spaces, by using Kakutani-Fan-Glicksberg fixed point theorem for upper semicontinuous set-valued mapping with nonempty closed acyclic values, and the closedness of  and
and  . The results in this paper generalize, extend, and unify some well-known some existence theorems in the literature.
. The results in this paper generalize, extend, and unify some well-known some existence theorems in the literature.
2. Preliminaries
Let  be the standard
be the standard  -dimensional simplex in
-dimensional simplex in  with vertices
with vertices  . For any nonempty subset
. For any nonempty subset  of
of  , we denote
, we denote  by the convex hull of the vertices
by the convex hull of the vertices  . The following definition was essentially given by Park and Kim [29].
. The following definition was essentially given by Park and Kim [29].
Definition 2.1.
A generalised convex space, or say, a  -convex space
-convex space  consists of a topological space
consists of a topological space  , a nonempty subset
, a nonempty subset  of
of  and a function
and a function  such that
such that
(i)for each  if
if  ,
,
(ii)for each  with
with  , there exists a continuous function
, there exists a continuous function  such that
such that  for each
for each  , where
, where  and
and  denotes the face of
denotes the face of  corresponding to the subindex of
corresponding to the subindex of  in
in  .
.
A subset  of the
of the  -convex space
-convex space  is said to be
is said to be  -convex if for each
-convex if for each  for all
for all  . For the convenience of our discussion, we also denote
. For the convenience of our discussion, we also denote  by
by  or
or  if there is no confusion for
if there is no confusion for  , where
, where  is the set of all indices for the set
is the set of all indices for the set  ; that is,
; that is,  . A space
. A space  is said to have a
is said to have a  -convex structure if and only if
-convex structure if and only if  is a
is a  -convex space.
-convex space.
In order to cover general economic models without linear convex structures, Park and Kim [29] introduced another abstract convexity notion called a  -convex space, which includes many abstract convexity notions such as
-convex space, which includes many abstract convexity notions such as  -convex spaces as special cases. For the details on G-convex spaces, see [30–34], where basic theory was extensively developed.
-convex spaces as special cases. For the details on G-convex spaces, see [30–34], where basic theory was extensively developed.
Definition 2.2.
A  -convex
-convex  is said to be a locally
is said to be a locally  -convex space if
-convex space if  is a uniform topological space with uniformity
is a uniform topological space with uniformity  , which has an open base
, which has an open base  of symmetric entourages such that for each
of symmetric entourages such that for each  , the set
, the set  is a
is a  -convex set for each
-convex set for each  .
.
We recall that a nonempty space is said to be acyclic if all of its reduced Čech homology groups over the rationals vanish.
Definition 2.3 (see [35]).
Let  be a topological space. A subset
be a topological space. A subset  of
of  is called contractible at
is called contractible at  , if there is a continuous mapping
, if there is a continuous mapping  such that
such that  for all
for all  and
and  for all
for all  .
.
In particular, each contractible space is acyclic and thus any nonempty convex or star-shaped set is acyclic. Moreover, by the definition of contractible set, we see that each convex space is contractible.
Definition 2.4.
Let  and
and  be two topological vector spaces and
be two topological vector spaces and  a nonempty subset of
a nonempty subset of  , and let
, and let  be a set-valued mapping.
be a set-valued mapping.
(i) is called upper
is called upper  -continuous at
-continuous at  if, for any neighbourhood
if, for any neighbourhood  of the origin in
of the origin in  , there is a neighbourhood
, there is a neighbourhood  of
of  such that, for all
such that, for all  ,
,

(ii) is called lower
is called lower  -continuous at
-continuous at  if, for any neighbourhood
if, for any neighbourhood  of the origin in
of the origin in  , there is a neighbourhood
, there is a neighbourhood  of
of  such that for all
such that for all  ,
,

Definition 2.5.
Let  and
and  be two topological vector spaces and
be two topological vector spaces and  a nonempty convex subset of
a nonempty convex subset of  . A set-valued mapping
. A set-valued mapping  is said to be properly
is said to be properly  -quasiconvex if, for any
-quasiconvex if, for any  and
and  , we have
, we have

Definition 2.6.
Let  and
and  be two topological vector spaces and
be two topological vector spaces and  a set-valued mapping.
a set-valued mapping.
(i) is said to be upper semicontinuous at
is said to be upper semicontinuous at  if, for any open set
if, for any open set  containing
containing  , there exists an open set
, there exists an open set  containing
containing  such that for all
such that for all  ,
,  ;
;  is said to be upper semicontinuous on
is said to be upper semicontinuous on  if it is upper semicontinuous at all
if it is upper semicontinuous at all  .
.
(ii) is said to be lower semicontinuous at
is said to be lower semicontinuous at  if, for any open set
if, for any open set  with
with  , there exists an open set
, there exists an open set  containing
containing  such that for all
such that for all  ,
,  ;
;  is said to be lower semicontinuous on
is said to be lower semicontinuous on  if it is lower semicontinuous at all
if it is lower semicontinuous at all  .
.
(iii) is said to be continuous on
is said to be continuous on  if it is at the same time upper semicontinuous and lower semicontinuous on
if it is at the same time upper semicontinuous and lower semicontinuous on  .
.
(iv) is said to be closed if the graph,
is said to be closed if the graph,  , of
, of  , that is,
, that is,  , is a closed set in
, is a closed set in  .
.
Lemma 2.7 (see [36]).
Let  and
and  be two Hausdorff topological vector spaces and
be two Hausdorff topological vector spaces and  a set-valued mapping. Then, the following properties hold:
a set-valued mapping. Then, the following properties hold:
(i)if  is closed and
is closed and  is compact, then
is compact, then  is upper semicontinuous, where
is upper semicontinuous, where  and
and  denotes the closure of the set
denotes the closure of the set  ,
,
(ii)if  is upper semicontinuous and for any
is upper semicontinuous and for any  is closed, then
is closed, then  is closed,
is closed,
(iii) is lower semicontinuous at
is lower semicontinuous at  if and only if for any
if and only if for any  and any net
and any net  , there exists a net
, there exists a net  such that
such that  and
and  .
.
We now have the following fixed point theorem in locally  -convex spaces given by Yuan [28] which is a generalization of the Fan-Glickberg-type fixed point theorems for upper semicontinuous set-valued mapping with nonempty closed acyclic values given in several places (e.g., see Kirk and Shin [37], Park and Kim [29], and others in locally convex spaces).
-convex spaces given by Yuan [28] which is a generalization of the Fan-Glickberg-type fixed point theorems for upper semicontinuous set-valued mapping with nonempty closed acyclic values given in several places (e.g., see Kirk and Shin [37], Park and Kim [29], and others in locally convex spaces).
Lemma 2.8 (see [28]).
Let  be a compact locally
be a compact locally  -convex space and
-convex space and  an upper semicontinuous set-valued mappings with nonempty closed acyclic values. Then,
an upper semicontinuous set-valued mappings with nonempty closed acyclic values. Then,  has a fixed point; that is, there exists an
has a fixed point; that is, there exists an  such that
such that  .
.
3. Main Results
In this section, we apply the Kakutani-Fan-Glicksberg fixed point theorem for upper semicontinuous set-valued mapping with nonempty closed acyclic values to establish two existence theorems of strong solutions and obtain the closedness of the strong solutions set for generalized strong vector quasiequilibrium problem.
Theorem 3.1.
Let  ,
,  , and
, and  be real locally
be real locally  -convex topological vector spaces,
-convex topological vector spaces,  and
and  nonempty compact subsets, and
nonempty compact subsets, and  a nonempty closed convex cone. Let
a nonempty closed convex cone. Let  be a continuous set-valued mapping such that for any
be a continuous set-valued mapping such that for any  , the set
, the set  is a nonempty closed contractible subset of
is a nonempty closed contractible subset of  . Let
. Let  be an upper semicontinuous set-valued mapping with nonempty closed acyclic values and
be an upper semicontinuous set-valued mapping with nonempty closed acyclic values and  a set-valued mapping satisfy the following conditions:
a set-valued mapping satisfy the following conditions:
(i)for all  ,
,
(ii)for all  are properly
are properly  -quasiconvex,
-quasiconvex,
(iii) are upper
are upper  -continuous,
-continuous,
(iv)for all  are lower
are lower  -continuous.
-continuous.
Then, the solutions set  is nonempty and closed subset of
is nonempty and closed subset of  .
.
Proof.
For any  , we define a set-valued mapping
, we define a set-valued mapping  by
by

Since for any  is nonempty. So, by assumption (i), we have that
is nonempty. So, by assumption (i), we have that  is nonempty. Next, we divide the proof into five steps.
is nonempty. Next, we divide the proof into five steps.
Step 1 (to show that  is acyclic).
is acyclic).
Since every contractible set is acyclic, it is enough to show that  is contractible. Let
is contractible. Let  , thus
, thus  and
and  . Since
. Since  is contractible, there exists a continuous mapping
is contractible, there exists a continuous mapping  such that
such that  and
and  . Now, we set
. Now, we set  for all
for all  . Then,
. Then,  is a continuous mapping, and we see that
is a continuous mapping, and we see that  and
and  for all
for all  . Let
. Let  . We claim that
. We claim that  . In fact, if
. In fact, if  , then there exists
, then there exists  such that
such that

Since  is properly
is properly  -quasiconvex, we can assume that
-quasiconvex, we can assume that

It follows that

which contradicts  . Therefore,
. Therefore,  , and hence
, and hence  is contractible.
is contractible.
Step 2 (to show that  is a closed subset of
is a closed subset of  ).
).
Let  be a sequence in
be a sequence in  such that
such that  . Then,
. Then,  . Since
. Since  is a closed subset of
is a closed subset of  ,
,  . Since
. Since  is a lower semicontinuous, it follows by Lemma 2.7(iii) that for any
is a lower semicontinuous, it follows by Lemma 2.7(iii) that for any  and any net
and any net  , there exists a net
, there exists a net  such that
such that  and
and  . This implies that
. This implies that

Since  are lower
are lower  -continuous, we note that for any neighbourhood
-continuous, we note that for any neighbourhood  of the origin in
of the origin in  , there exists a subnet
, there exists a subnet  of
of  such that
such that

From (3.5) and (3.6), we have

We claim that  . Assume that there exists
. Assume that there exists  and
and  . Then, we note that
. Then, we note that  , and the set
, and the set  is closed. Thus,
is closed. Thus,  is open, and
is open, and  . Since
. Since  is a locally
is a locally  -convex space, there exists a neighbourhood
-convex space, there exists a neighbourhood  of the origin such that
of the origin such that  and
and  . Thus, we note that
. Thus, we note that  , and hence
, and hence  , which contradicts to (3.7). Hence,
, which contradicts to (3.7). Hence,  , and therefore,
, and therefore,  . Then,
. Then,  is a closed subset of
is a closed subset of  .
.
Step 3 (to show that  is upper semicontinuous).
is upper semicontinuous).
Let  be given such that
be given such that  , and let
, and let  such that
such that  . Since
. Since  and
and  is upper semicontinuous, it follows by Lemma 2.7(ii) that
is upper semicontinuous, it follows by Lemma 2.7(ii) that  . We claim that
. We claim that  . Assume that
. Assume that  . Then, there exists
. Then, there exists  such that
such that

which implies that there is a neighbourhood  of the origin in
of the origin in  such that
such that

Since  is upper
is upper  -continuous, it follows that for any neighbourhood
-continuous, it follows that for any neighbourhood  of the origin in
of the origin in  , there exists a neighbourhood
, there exists a neighbourhood  of
of  such that
such that

Without loss of generality, we can assume that  . This implies that
. This implies that

Thus, there is  such that
such that

it is a contradiction to  . Hence,
. Hence,  , and therefore,
, and therefore,  is a closed mapping. Since
is a closed mapping. Since  is a compact set and
is a compact set and  is a closed subset of
is a closed subset of  ,
,  is compact. This implies that
is compact. This implies that  is compact. Then, by Lemma 2.7(i), we have
is compact. Then, by Lemma 2.7(i), we have  is upper semicontinuous.
is upper semicontinuous.
Step 4 (to show that the solutions set  is nonempty).
is nonempty).
Define the set-valued mapping  by
by

Then,  is an upper semicontinuous mpping. Moreover, we note that
is an upper semicontinuous mpping. Moreover, we note that  is a nonempty closed acyclic subset of
is a nonempty closed acyclic subset of  for all
for all  . By Lemma 2.8, there exists a point
. By Lemma 2.8, there exists a point  such that
such that  . Thus, we have
. Thus, we have  ,
,  . It follows that there exists
. It follows that there exists  and
and  such that
such that  and
and

Hence, the solutions set  .
.
Step 5 (to show that the solutions set  is closed).
is closed).
Let  be a net in
be a net in  such that
such that  . By definition of the solutions set
. By definition of the solutions set  , we note that
, we note that  , and there exist
, and there exist  satisfying
satisfying

Since  is a continuous closed valued mapping,
is a continuous closed valued mapping,  . From the compactness of
. From the compactness of  , we can assume that
, we can assume that  . Since
. Since  is an upper semicontinuous closed valued mapping, it follows by Lemma 2.7(ii) that
is an upper semicontinuous closed valued mapping, it follows by Lemma 2.7(ii) that  is closed. Thus, we have
is closed. Thus, we have  . Since
. Since  is a lower
is a lower  -continuous, we have
-continuous, we have

This means that  belongs to
belongs to  . Therefore, the solutions set
. Therefore, the solutions set  is closed. This completes the proof.
is closed. This completes the proof.
Theorem 3.1 extends Theorem 3.1 of Long et al. [16] to locally  -convex which includes locally convex Hausdorff topological vector spaces.
-convex which includes locally convex Hausdorff topological vector spaces.
Corollary 3.2.
Let  ,
,  and
and  be real locally convex Hausdorff topological vector spaces,
be real locally convex Hausdorff topological vector spaces,  and
and  two nonempty compact convex subsets, and
two nonempty compact convex subsets, and  a nonempty closed convex cone. Let
a nonempty closed convex cone. Let  be a continuous set-valued mapping such that for any
be a continuous set-valued mapping such that for any  ,
,  is a nonempty closed convex subset of
is a nonempty closed convex subset of  . Let
. Let  be an upper semicontinuous set-valued mapping such that for any
be an upper semicontinuous set-valued mapping such that for any  ,
,  is a nonempty closed convex subset of
is a nonempty closed convex subset of  . Let
. Let  be a set-valued mapping satisfying the following conditions:
be a set-valued mapping satisfying the following conditions:
(i)for all  ,
,
(ii)for all  are properly
are properly  -quasiconvex,
-quasiconvex,
(iii) are upper
are upper  -continuous,
-continuous,
(iv)for all  are lower
are lower  -continuous.
-continuous.
Then, the solutions set  is nonempty and closed subset of
is nonempty and closed subset of  .
.
Theorem 3.3.
Let  ,
,  and
and  be real locally
be real locally  -convex topological vector spaces,
-convex topological vector spaces,  and
and  nonempty compact subsets, and
nonempty compact subsets, and  a nonempty closed convex cone. Let
a nonempty closed convex cone. Let  be a continuous set-valued mapping such that for any
be a continuous set-valued mapping such that for any  , the set
, the set  is a nonempty closed contractible subset of
is a nonempty closed contractible subset of  . Let
. Let  be an upper semicontinuous set-valued mapping with nonempty closed acyclic values and
be an upper semicontinuous set-valued mapping with nonempty closed acyclic values and  a set-valued mapping satisfying the following conditions:
a set-valued mapping satisfying the following conditions:
(i)for all  ,
,
(ii)for all  are properly
are properly  -quasiconvex,
-quasiconvex,
(iii) are upper
are upper  -continuous,
-continuous,
(iv)for all  are lower
are lower  -continuous.
-continuous.
Then, the solutions set  is nonempty and closed subset of
is nonempty and closed subset of  .
.
Proof.
For any  , define a set-valued mapping
, define a set-valued mapping  by
by

Proceeding as in the proof of Theorem 3.1, we need to prove that  is closed acyclic subset of
is closed acyclic subset of  for all
for all  . We divide the remainder of the proof into three steps.
. We divide the remainder of the proof into three steps.
Step 1 (to show that  is a closed subset of
is a closed subset of  ).
).
Let  be a sequence in
be a sequence in  such that
such that  . Then,
. Then,  and
and  . Since
. Since  is a closed subset of
is a closed subset of  , we have
, we have  . By the lower semicontinuity of
. By the lower semicontinuity of  and Lemma 2.7(iii), we note that for any
and Lemma 2.7(iii), we note that for any  and any net
and any net  , there exists a net
, there exists a net  such that
such that  and
and  . Thus, we have
. Thus, we have

which implies that there exists a neighbourhood  of the origin in
of the origin in  such that
such that

Since  are lower
are lower  -continuous, it follows that for any neighbourhood
-continuous, it follows that for any neighbourhood  of the origin in
of the origin in  , there exists a subnet
, there exists a subnet  of
of  such that
such that

Without loss of generality, we can assume that  . Then, by (3.18), (3.19), and (3.20), we have
. Then, by (3.18), (3.19), and (3.20), we have

This means that  and so
and so  is a closed subset of
is a closed subset of  .
.
Step 2 (to show that  is upper semicontinuous).
is upper semicontinuous).
Let  be given such that
be given such that  , and let
, and let  such that
such that  . Then,
. Then,  and
and  . Since
. Since  is upper semicontinuous closed valued mapping, it follows by Lemma 2.7(ii) that
is upper semicontinuous closed valued mapping, it follows by Lemma 2.7(ii) that  . We claim that
. We claim that  . Indeed, if
. Indeed, if  , then there exists a
, then there exists a  such that
such that

Since  is upper
is upper  -continuous, we note that for any neighbourhood
-continuous, we note that for any neighbourhood  of the origin in
of the origin in  , there exists a neighbourhood
, there exists a neighbourhood  of
of  such that
such that

From (3.22) and (3.23), we obtain

As in the proof of Step 2 in Theorem 3.1, we can show that  for all
for all  . Hence, there is
. Hence, there is  such that
such that

it is a contradiction to  . Hence,
. Hence,  , and therefore,
, and therefore,  is a closed mapping. Since
is a closed mapping. Since  is a compact set and
is a compact set and  is a closed subset of
is a closed subset of  ,
,  is compact. This implies that
is compact. This implies that  is compact. Then, by Lemma 2.7(i), we have that
is compact. Then, by Lemma 2.7(i), we have that  is upper semicontinuous.
is upper semicontinuous.
Step 3 (to show that the solutions set  is nonempty and closed).
is nonempty and closed).
Define the set-valued mapping  by
by

Then,  is an upper semicontinuous mapping. Moreover, we note that
is an upper semicontinuous mapping. Moreover, we note that  is a nonempty closed acyclic subset of
is a nonempty closed acyclic subset of  for all
for all  . Hence, by Lemma 2.8, there exists a point
. Hence, by Lemma 2.8, there exists a point  such that
such that  . Thus, we have
. Thus, we have  and
and  . This implies that there exists
. This implies that there exists  and
and  such that
such that  and
and

Hence,  . Similarly, by the proof of Step 5 in Theorem 3.1, we have
. Similarly, by the proof of Step 5 in Theorem 3.1, we have  is closed. This completes the proof.
is closed. This completes the proof.
4. Stability
In this section, we discuss the stability of the solutions for the generalized strong vector quasiequilibrium problem (GSVQEP II).
Throughout this section, let  ,
,  be Banach spaces, and let
be Banach spaces, and let  be a real locally
be a real locally  -convex Hausdorff topological vector space. Let
-convex Hausdorff topological vector space. Let  and
and  be nonempty compact subsets, and let
be nonempty compact subsets, and let  be a nonempty closed convex cone. Let
be a nonempty closed convex cone. Let  is a continuous set-valued mapping with nonempty closed contractible values, and
is a continuous set-valued mapping with nonempty closed contractible values, and  is an upper semicontinuous set-valued mapping with nonempty closed acyclic values}.
is an upper semicontinuous set-valued mapping with nonempty closed acyclic values}.
Let  be compact sets in a normed space. Recall that the Hausdorff metric is defined by
be compact sets in a normed space. Recall that the Hausdorff metric is defined by

where  .
.
For  , we define
, we define

where  being the appropriate Hausdorff metrics. Obviously,
being the appropriate Hausdorff metrics. Obviously,  is a metric space. Now, we assume that
is a metric space. Now, we assume that  satisfies the assumptions of Theorem 3.3. Then, for each
satisfies the assumptions of Theorem 3.3. Then, for each  , (GSVQEP II) has a solution
, (GSVQEP II) has a solution  . Let
. Let

Thus,  , which conclude that
, which conclude that  defines a set-valued mapping from
defines a set-valued mapping from  into
into  .
.
We also need the following lemma in the sequel.
Let  be a metric space, and let
be a metric space, and let  be compact sets in
be compact sets in  . Suppose that for any open set
. Suppose that for any open set  , there exists
, there exists  such that
such that  for all
for all  . Then, any sequence
. Then, any sequence  satisfying
satisfying  has a convergent subsequence with limit in
has a convergent subsequence with limit in  .
.
In the following theorem, we replaced the convex set by the contractible set and acyclic set in Theorem 4.1 in [16]. The following theorem can acquire the same result appearing on the Theorem 4.1 by utilized Lemma 4.1. Now, we need only to present stability theorem for the solution set mapping  for (GSVQEP II).
for (GSVQEP II).
Theorem 4.2.
 is an upper semicontinuous mapping with compact values.
is an upper semicontinuous mapping with compact values.
Proof.
Since  is compact, we need only to show that
is compact, we need only to show that  is a closed mapping. In fact, let
is a closed mapping. In fact, let  be such that
be such that  . Since
. Since  , we have
, we have  , and there exists
, and there exists  such that
such that

By the same argument as in the proof of Theorem 4.1 in [16], we can show that  and
and  .
.
Since  is lower semicontinuous at
is lower semicontinuous at  and
and  , it follows by Lemma 2.7(iii) that for any
, it follows by Lemma 2.7(iii) that for any  , there exists
, there exists  such that
such that  . To finish the proof of the theorem, we need to show that
. To finish the proof of the theorem, we need to show that  for all
for all  . Since
. Since  , it follows by the same argument as in the proof of Theorem 4.1 in [16] that there exists a subsequence
, it follows by the same argument as in the proof of Theorem 4.1 in [16] that there exists a subsequence  of
of  such that
such that  ,
,  ,
,  , and
, and

From the upper  -continuous of
-continuous of  , we have
, we have

Then,  , and so
, and so  is closed. The theorem is proved.
is closed. The theorem is proved.
References
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994,63(1–4):123–145.
Bianchi M, Schaible S: Generalized monotone bifunctions and equilibrium problems. Journal of Optimization Theory and Applications 1996,90(1):31–43. 10.1007/BF02192244
Oettli W, Schläger D: Existence of equilibria for monotone multivalued mappings. Mathematical Methods of Operations Research 1998,48(2):219–228. 10.1007/s001860050024
Ansari QH, Oettli W, Schläger D: A generalization of vectorial equilibria. Mathematical Methods of Operations Research 1997,46(2):147–152. 10.1007/BF01217687
Bianchi M, Hadjisavvas N, Schaible S: Vector equilibrium problems with generalized monotone bifunctions. Journal of Optimization Theory and Applications 1997,92(3):527–542. 10.1023/A:1022603406244
Debreu G: A social equilibrium existence theorem. Proceedings of the National Academy of Sciences of the United States of America 1952, 38: 886–893. 10.1073/pnas.38.10.886
Fu J-Y: Generalized vector quasi-equilibrium problems. Mathematical Methods of Operations Research 2000,52(1):57–64. 10.1007/s001860000058
Gianness F (Ed): Vector Variational Inequalities and Vector Equilibria. Mathematical Theories, Nonconvex Optimization and Its Applications. Volume 38. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:xiv+523.
Gong X: Strong vector equilibrium problems. Journal of Global Optimization 2006,36(3):339–349. 10.1007/s10898-006-9012-5
Gong XH: Efficiency and Henig efficiency for vector equilibrium problems. Journal of Optimization Theory and Applications 2001,108(1):139–154. 10.1023/A:1026418122905
Holmes RB: Geometric Functional Analysis and Its Applications. Springer, New York, NY, USA; 1975:x+246. Graduate Texts in Mathematics, no. 2
Hou SH, Gong XH, Yang XM: Existence and stability of solutions for generalized Ky fan inequality problems with trifunctions. Journal of Optimization Theory and Applications 2010,146(2):387–398. 10.1007/s10957-010-9656-7
Huang NJ, Li J, Thompson HB: Stability for parametric implicit vector equilibrium problems. Mathematical and Computer Modelling 2006,43(11–12):1267–1274. 10.1016/j.mcm.2005.06.010
Li SJ, Teo KL, Yang XQ: Generalized vector quasi-equilibrium problems. Mathematical Methods of Operations Research 2005,61(3):385–397. 10.1007/s001860400412
Lin L-J, Park S: On some generalized quasi-equilibrium problems. Journal of Mathematical Analysis and Applications 1998,224(2):167–181. 10.1006/jmaa.1998.5964
Long X-J, Huang N-J, Teo K-l: Existence and stability of solutions for generalized strong vector quasi-equilibrium problem. Mathematical and Computer Modelling 2008,47(3–4):445–451. 10.1016/j.mcm.2007.04.013
Ansari QH: Vector equilibrium problems and vector variational inequalities. In Vector Variational Inequalities and Vector Equilibria, Nonconvex Optim. Appl.. Volume 38. Edited by: Giannessi F. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:1–15. 10.1007/978-1-4613-0299-5_1
Tan NX, Tinh PN: On the existence of equilibrium points of vector functions. Numerical Functional Analysis and Optimization 1998,19(1–2):141–156. 10.1080/01630569808816820
Ansari QH, Yao J-C: On vector quasi-equilibrium problems. In Equilibrium Problems and Variational Models (Erice, 2000), Nonconvex Optim. Appl.. Volume 68. Edited by: Maugeri A, Giannessi F. Kluwer Academic Publishers, Norwell, Mass, USA; 2003:1–18.
Ansari QH, Konnov IV, Yao JC: On generalized vector equilibrium problems. Nonlinear Analysis: Theory, Methods & Applications 2001,47(1):543–554. 10.1016/S0362-546X(01)00199-7
Ansari QH, Yao J-C: An existence result for the generalized vector equilibrium problem. Applied Mathematics Letters 1999,12(8):53–56. 10.1016/S0893-9659(99)00121-4
Konnov IV, Yao JC: Existence of solutions for generalized vector equilibrium problems. Journal of Mathematical Analysis and Applications 1999,233(1):328–335. 10.1006/jmaa.1999.6312
Ansari QH, Siddiqi AH, Wu SY: Existence and duality of generalized vector equilibrium problems. Journal of Mathematical Analysis and Applications 2001,259(1):115–126. 10.1006/jmaa.2000.7397
Georgiev PGr, Tanaka T: Vector-valued set-valued variants of Ky Fan's inequality. Journal of Nonlinear and Convex Analysis 2000,1(3):245–254.
Song W: Vector equilibrium problems with set-valued mappings. In Vector Variational Inequalities and Vector Equilibria, Nonconvex Optim. Appl.. Volume 38. Edited by: Giannessi F. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000:403–422. 10.1007/978-1-4613-0299-5_24
Ansari QH, Flores-Bazán F: Generalized vector quasi-equilibrium problems with applications. Journal of Mathematical Analysis and Applications 2003,277(1):246–256. 10.1016/S0022-247X(02)00535-8
Hou SH, Yu H, Chen GY: On vector quasi-equilibrium problems with set-valued maps. Journal of Optimization Theory and Applications 2003,119(3):485–498.
Yuan GX-Z: Fixed points of upper semicontinuous mappings in locally
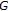 -convex spaces. Bulletin of the Australian Mathematical Society 1998,58(3):469–478. 10.1017/S0004972700032457
-convex spaces. Bulletin of the Australian Mathematical Society 1998,58(3):469–478. 10.1017/S0004972700032457Park S, Kim H: Admissible classes of multifunctions on generalized convex spaces. Proceedings of the College of Natural Sciences 1993, 18: 1–21.
Park S: Fixed points of better admissible maps on generalized convex spaces. Journal of the Korean Mathematical Society 2000,37(6):885–899.
Park S: New topological versions of the Fan-Browder fixed point theorem. Nonlinear Analysis: Theory, Methods & Applications 2001,47(1):595–606. 10.1016/S0362-546X(01)00204-8
Park S: Fixed point theorems in locally
 -convex spaces. Nonlinear Analysis: Theory, Methods & Applications 2002,48(6):869–879. 10.1016/S0362-546X(00)00220-0
-convex spaces. Nonlinear Analysis: Theory, Methods & Applications 2002,48(6):869–879. 10.1016/S0362-546X(00)00220-0Park S: Remarks on acyclic versions of generalized von Neumann and Nash equilibrium theorems. Applied Mathematics Letters 2002,15(5):641–647. 10.1016/S0893-9659(02)80018-0
Park S: Fixed points of approximable or Kakutani maps in generalized convex spaces. Journal of Nonlinear and Convex Analysis 2006,7(1):1–17.
Bardaro C, Ceppitelli R: Some further generalizations of Knaster-Kuratowski-Mazurkiewicz theorem and minimax inequalities. Journal of Mathematical Analysis and Applications 1988,132(2):484–490. 10.1016/0022-247X(88)90076-5
Aubin J-P, Ekeland I: Applied Nonlinear Analysis, Pure and Applied Mathematics (New York). John Wiley & Sons, New York, NY, USA; 1984:xi+518.
Kirk WA, Shin SS: Fixed point theorems in hyperconvex spaces. Houston Journal of Mathematics 1997,23(1):175–188.
Yu J: Essential weak efficient solution in multiobjective optimization problems. Journal of Mathematical Analysis and Applications 1992,166(1):230–235. 10.1016/0022-247X(92)90338-E
Acknowledgments
S. Plubtieng would like to thank the Thailand Research Fund for financial support under Grant no. BRG5280016. Moreover, K. Sitthithakerngkiet would like to thank the Office of the Higher Education Commission, Thailand, for supporting by grant fund under Grant no. CHE-Ph.D-SW-RG/41/2550, Thailand.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Plubtieng, S., Sitthithakerngkiet, K. Existence Result of Generalized Vector Quasiequilibrium Problems in Locally 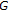 -Convex Spaces.
Fixed Point Theory Appl 2011, 967515 (2011). https://doi.org/10.1155/2011/967515
-Convex Spaces.
Fixed Point Theory Appl 2011, 967515 (2011). https://doi.org/10.1155/2011/967515
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/967515
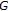 -convex spaces. Bulletin of the Australian Mathematical Society 1998,58(3):469–478. 10.1017/S0004972700032457
-convex spaces. Bulletin of the Australian Mathematical Society 1998,58(3):469–478. 10.1017/S0004972700032457 -convex spaces. Nonlinear Analysis: Theory, Methods & Applications 2002,48(6):869–879. 10.1016/S0362-546X(00)00220-0
-convex spaces. Nonlinear Analysis: Theory, Methods & Applications 2002,48(6):869–879. 10.1016/S0362-546X(00)00220-0