Skip to main content
Fixed Point Theory and Algorithms for Sciences and Engineering
Download PDF

Viscosity approximation fixed points for nonexpansive and 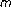-accretive operators

Fixed Point Theory and Applications volume 2006, Article number: 81325 (2006) Cite this article

Abstract

Let be a real reflexive Banach space, let be a closed convex subset of , and let be an -accretive operator with a zero. Consider the iterative method that generates the sequence by the algorithm where and are two sequences satisfying certain conditions, denotes the resolvent for , and let be a fixed contractive mapping. The strong convergence of the algorithm is proved assuming that has a weakly continuous duality map.

[12345678]

References

  1. Barbu V: Nonlinear Semigroups and Differential Equations in Banach Spaces. Editura Academiei Republicii Socialiste România, Bucharest; Noordhoff, Leiden; 1976:352.

    Book  Google Scholar 

  2. Browder FE: Convergence of approximants to fixed points of nonexpansive non-linear mappings in Banach spaces. Archive for Rational Mechanics and Analysis 1967,24(1):82–90.

    Article  MathSciNet  MATH  Google Scholar 

  3. Browder FE: Convergence theorems for sequences of nonlinear operators in Banach spaces. Mathematische Zeitschrift 1967,100(3):201–225. 10.1007/BF01109805

    Article  MathSciNet  MATH  Google Scholar 

  4. Lim T-C, Xu H-K: Fixed point theorems for asymptotically nonexpansive mappings. Nonlinear Analysis 1994,22(11):1345–1355. 10.1016/0362-546X(94)90116-3

    Article  MathSciNet  MATH  Google Scholar 

  5. Xu H-K: Iterative algorithms for nonlinear operators. Journal of the London Mathematical Society. Second Series 2002,66(1):240–256. 10.1112/S0024610702003332

    Article  MathSciNet  MATH  Google Scholar 

  6. Xu H-K: An iterative approach to quadratic optimization. Journal of Optimization Theory and Applications 2003,116(3):659–678. 10.1023/A:1023073621589

    Article  MathSciNet  MATH  Google Scholar 

  7. Xu H-K: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004,298(1):279–291. 10.1016/j.jmaa.2004.04.059

    Article  MathSciNet  MATH  Google Scholar 

  8. Xu H-K: Strong convergence of an iterative method for nonexpansive and accretive operators. Journal of Mathematical Analysis and Applications 2006,314(2):631–643. 10.1016/j.jmaa.2005.04.082

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Tianjin Polytechnic University, Tianjin, 300160, China

    Rudong Chen & Zhichuan Zhu

Authors
  1. Rudong Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhichuan Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rudong Chen.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and Permissions

About this article

Cite this article

Chen, R., Zhu, Z. Viscosity approximation fixed points for nonexpansive and 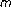-accretive operators. Fixed Point Theory Appl 2006, 81325 (2006). https://doi.org/10.1155/FPTA/2006/81325

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1155/FPTA/2006/81325

Keywords

  • Differential Geometry
  • Computational Biology