- Research Article
- Open access
- Published:
Fixed point theorems in 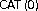 spaces and
spaces and  -trees
-trees
Fixed Point Theory and Applications volume 2004, Article number: 738084 (2004)
Abstract
We show that if  is a bounded open set in a complete
is a bounded open set in a complete  space
space  , and if
, and if  is nonexpansive, then
is nonexpansive, then  always has a fixed point if there exists
always has a fixed point if there exists  such that
such that  for all
for all  . It is also shown that if
. It is also shown that if  is a geodesically bounded closed convex subset of a complete
is a geodesically bounded closed convex subset of a complete  -tree with
-tree with  , and if
, and if  is a continuous mapping for which
is a continuous mapping for which  for some
for some  and all
and all  , then
, then  has a fixed point. It is also noted that a geodesically bounded complete
has a fixed point. It is also noted that a geodesically bounded complete  -tree has the fixed point property for continuous mappings. These latter results are used to obtain variants of the classical fixed edge theorem in graph theory.
-tree has the fixed point property for continuous mappings. These latter results are used to obtain variants of the classical fixed edge theorem in graph theory.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kirk, W. Fixed point theorems in 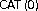 spaces and
spaces and  -trees.
Fixed Point Theory Appl 2004, 738084 (2004). https://doi.org/10.1155/S1687182004406081
-trees.
Fixed Point Theory Appl 2004, 738084 (2004). https://doi.org/10.1155/S1687182004406081
Received:
Published:
DOI: https://doi.org/10.1155/S1687182004406081