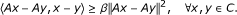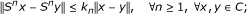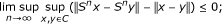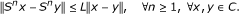An extragradient-like approximation method for variational inequalities and fixed point problems

Abstract

The purpose of this paper is to investigate the problem of finding a common element of the set of fixed points of an asymptotically strict pseudocontractive mapping in the intermediate sense and the set of solutions of a variational inequality problem for a monotone and Lipschitz continuous mapping. We introduce an extragradient-like iterative algorithm that is based on the extragradient-like approximation method and the modified Mann iteration process. We establish a strong convergence theorem for two sequences generated by this extragradient-like iterative algorithm. Utilizing this theorem, we also design an iterative process for finding a common fixed point of two mappings, one of which is an asymptotically strict pseudocontractive mapping in the intermediate sense and the other taken from the more general class of Lipschitz pseudocontractive mappings.

1991 MSC: 47H09; 47J20.

1. Introduction

Let H be a real Hilbert space whose inner product and norm are denoted by 〈·,·〉 and || · ||, respectively, and let C be a nonempty closed convex subset of H. Corresponding to an operator A : C → H and set C, the variational inequality problem VIP(A, C) is defined as follows:

(1.1)

The set of solutions of VIP(A, C) is denoted by Ω. It is well known that if A is a strongly monotone and Lipschitz-continuous mapping on C, then the VIP(A, C) has a unique solution. Not only the existence and uniqueness of a solution are important topics in the study of the VIP(A, C) but also how to compute a solution of the VIP(A, C) is important. For applications and further details on VIP(A, C), we refer to [1–4] and the references therein.

The set of fixed points of a mapping S is denoted by Fix(S), that is, Fix(S) = {x ∈ H : Sx = x}.

For finding an element of F(S) ∩ Ω under the assumption that a set C ⊂ H is nonempty, closed and convex, a mapping S : C → C is nonexpansive and a mapping A : C → H is β-inverse-strongly monotone, Takahashi and Toyoda [5] proposed an iterative scheme and proved that the sequence generated by the proposed scheme converges weakly to a point z ∈ F(S) ∩ Ω if F(S) ∩ Ω ≠ ∅.

Recently, motivated by the idea of Korpelevich's extragradient method [6], Nadezhkina and Takahashi [7] introduced an iterative scheme, called extragradient method, for finding an element of F(S) ∩ Ω and established the weak convergence result. Very recently, inspired by the work in [7], Zeng and Yao [8] introduced an iterative scheme for finding an element of F(S) ∩ Ω and obtained the weak convergence result. The viscosity approximation method for finding a fixed point of a given nonexpansive mapping was proposed by Moudafi [9]. He proved the strong convergence of the sequence generated by the proposed method to a unique solution of some variational inequality. Xu [10] extended the results of [9] to the more general version. Later on, Ceng and Yao [11] also introduced an extragradient-like approximation method, which is based on the above extragradient method and viscosity approximation method, and proved the strong convergence result under certain conditions.

An iterative method for the approximation of fixed points of asymptotically nonexpansive mappings was developed by Schu [12]. Iterative methods for the approximation of fixed points of asymptotically nonexpansive mappings have been further studied in [13, 14] and the references therein. The class of asymptotically nonexpansive mappings in the intermediate sense was introduced by Bruck et al. [15]. The iterative methods for the approximation of fixed points of such types of non-Lipschitzian mappings have been further studied in [16–18]. On the other hand, Kim and Xu [19] introduced the concept of asymptotically κ-strict pseudocontractive mappings in a Hilbert space and studied the weak and strong convergence theorems for this class of mappings. Sahu et al. [20] considered the concept of asymptotically κ-strict pseudocontractive mappings in the intermediate sense, which are not necessarily Lipschitzian. They proposed modified Mann iteration process and proved its weak convergence for an asymptotically κ-strict pseudocontractive mapping in the intermediate sense.

Very recently, Ceng et al. [21] established the strong convergence of viscosity approximation method for a modified Mann iteration process for asymptotically strict pseudocontractive mappings in intermediate sense and then proved the strong convergence of general CQ algorithm for asymptotically strict pseudocontractive mappings in intermediate sense. They extended the concept of asymptotically strict pseudocontractive mappings in intermediate sense to Banach space setting, called nearly asymptotically κ-strict pseudocontractive mapping in intermediate sense.

They also established the weak convergence theorems for a fixed point of a nearly asymptotically κ-strict pseudocontractive mapping in intermediate sense which is not necessarily Lipschitzian.

In this paper, we propose and study an extragradient-like iterative algorithm that is based on the extragradient-like approximation method in [11] and the modified Mann iteration process in [20]. We apply the extragradient-like iterative algorithm to designing an iterative scheme for finding a common fixed point of two nonlinear mappings. Here, we remind the reader of the following facts: (i) the modified Mann iteration process in [[20], Theorem 3.4] is extended to develop the extragradient-like iterative algorithm for finding an element of F(S) ∩ Ω; (ii) the extragradient-like iterative algorithm is very different from the extragradient-like iterative scheme in [11] since the class of mappings S in our scheme is more general than the class of nonexpansive mappings.

2. Preliminaries

Throughout the paper, unless otherwise specified, we assume that H is a real Hilbert space whose inner product and norm are denoted by 〈·,·〉 and || · ||, respectively, and C is a nonempty closed convex subset of H. The set of fixed points of a mapping S is denoted by Fix(S), that is, Fix(S) = {x ∈ H : Sx = x}. We write x _n ⇀ x to indicate that the sequence {x _n } converges weakly to x. The sequence {x _n } converges strongly to x is denoted by x _n → x.

Recall that a mapping S : C → C is said to be L-Lipschitzian if there exists a constant L ≥ 0 such that ||Sx - Sy|| ≤ L||x - y||, ∀x, y ∈ C. In particular, if L ∈ [0, 1), then S is called a contraction on C; if L = 1, then S is called a nonexpansive mapping on C. The mapping S : C → C is called pseudocontractive if

A mapping A : C → H is called

• (i) monotone if

  

• (ii) β-inverse-strongly monotone [22, 23] if there exists a positive constant β such that

  

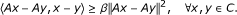
It is obvious that if A is β-inverse-strongly monotone, then A is monotone and Lipschitz continuous.

It is easy to see that if a mapping S : C → C is nonexpansive, then the mapping A = I - S is 1/2-inverse-strongly monotone; moreover, F(S) = Ω (see, e.g., [5]). At the same time, if a mapping S : C → C is pseudocontractive and L-Lipschitz continuous, then the mapping A = (I - S) is monotone and L + 1-Lipschitz continuous; moreover, F(S) = Ω (see, e.g., [[24], proof of Theorem 4.5]).

Definition 2.1. Let C be a nonempty subset of a normed space X. A mapping S : C → C is said to be

• (a) asymptotically nonexpansive [25] if there exists a sequence {k _n } of positive numbers such that lim_n→∞ K _n = 1 and

  

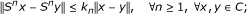
• (b) asymptotically nonexpansive in the intermediate sense [15] provided S is uniformly continuous and

  

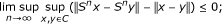
• (c) uniformly Lipschitzian if there exists a constant L > 0 such that

  

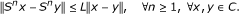
It is clear that every nonexpansive mapping is asymptotically nonexpansive and every asymptotically nonexpansive mapping is uniformly Lipschitzian.

The class of asymptotically nonexpansive mappings was introduced by Goebel and Kirk [25] as an important generalization of the class of nonexpansive mappings. The existence of fixed points of asymptotically nonexpansive mappings was proved by Goebel and Kirk [25] as below:

Theorem 2.1. [[25], Theorem 1] If C is a nonempty closed convex bounded subset of a uniformly convex Banach space, then every asymptotically nonexpansive mapping S : C → C has a fixed point in C.

Definition 2.2. [19] A mapping S : C → C is said to be an asymptotically κ-strict pseudocontractive mapping with sequence {γ _n } if there exist a constant κ ∈ [0, 1) and a sequence {γ _n } in [0, ∞) with lim_n→∞γ _n = 0 such that

(2.1)

It is important to note that every asymptotically κ-strict pseudocontractive mapping with sequence {γ _n } is a uniformly L-Lipschitzian mapping with .

Definition 2.3. [20] A mapping S : C → C is said to be an asymptotically κ-strict pseudocontractive mapping in the intermediate sense with sequence {γ _n } if there exist a constant κ ∈ [0, 1) and a sequence {γ _n } in [0, ∞) with lim_n→∞γ _n = 0 such that

(2.2)

Put

Then, c _n ≥ 0 (∀n ≥ 1), c _n → 0 (n → ∞) and (2.2) reduces to the relation

(2.3)

Whenever c _n = 0 for all n ≥ 1 in (2.3), then S is an asymptotically κ-strict pseudocontractive mapping with sequence {γ _n }.

For every point x ∈ H, there exists a unique nearest point in C, denoted by P _C x, such that

P _C is called the metric projection of H onto C. Recall that the inequality holds

(2.4)

Moreover, it is equivalent to

it is also equivalent to

(2.5)

It is easy to see that P _C is a nonexpansive mapping from H onto C; see, e.g., [26] for further detail.

Lemma 2.1. Let A : C → H be a monotone mapping. Then,

Lemma 2.2. Let H be a real Hilbert space. Then, the following hold:

Lemma 2.3. [[20], Lemma 2.6] Let S : C → C be an asymptotically κ-strict pseudocontractive mapping in the intermediate sense with sequence {γ _n }. Then,

for all x, y ∈ C and n ≥ 1.

Lemma 2.4. [[20], Lemma 2.7] Let S : C → C be a uniformly continuous asymptotically κ-strict pseudocontractive mapping in the intermediate sense with sequence {γ _n }. Let {x _n } be a sequence in C such that ||x _n - x_n+1|| → 0 and ||x _n - Sⁿx _n || → 0 as n → ∞. Then, ||x _n - Sx _n || → 0 as n → ∞.

Proposition 2.1 (Demiclosedness Principle). [[20], Proposition 3.1] Let S : C → C be a continuous asymptotically κ-strict pseudocontractive mapping in the intermediate sense with sequence {γ _n }. Then, I - S is demiclosed at zero in the sense that if {x _n } is a sequence in C such that x _n ⇀ x ∈ C and lim sup_{m→ ∞}lim sup_{n→ ∞}||x _n S^mx _n || = 0, then (I - S)x = 0.

Proposition 2.2. [[20], Proposition 3.2] Let S : C → C be a continuous asymptotically κ-strict pseudocontractive mapping in the intermediate sense with sequence {γ _n } such that F (S) ≠ ∅. Then, F(S) is closed and convex.

Remark 2.1. Propositions 2.1 and 2.2 give some basic properties of an asymptotically κ-strict pseudocontractive mapping in the intermediate sense with sequence {γ _n }. Moreover, Proposition 2.1 extends the demiclosedness principles studied for certain classes of nonlinear mappings in [19, 27–29].

Lemma 2.5. [30]Let (X, 〈·,·〉) be an inner product space. Then, for all x, y, z ∈ X and all α, β, γ ∈ [0, 1] with α + β + γ = 1, we have

Lemma 2.6. [[31], Lemma 2.5] Let {s _n } be a sequence of nonnegative real numbers satisfying

where, , andsatisfy the conditions:

(i), or equivalently,;

(ii);

(iii).

Then, lim_n→∞s _n = 0.

Lemma 2.7. [32]Let {x _n } and {z _n } be bounded sequences in a Banach space X and let {ϱ _n } be a sequence in [0, 1] with 0 < lim inf_n→∞ϱ _n ≤ lim sup_n→∞ϱ _n ≤ 1. Suppose that x_n+1= ϱ _n x _n + (1 - ϱ _n )z _n for all integers n ≥ 1 and lim sup_n→∞(||z_n+1- z _n || - ||x_n+1- x _n ||) ≤ 0. Then, lim_n→∞||z _n - x _n || = 0.

The following lemma can be easily proved, and therefore, we omit the proof.

Lemma 2.8. In a real Hilbert space H, there holds the inequality

A set-valued mapping T : H → 2 ^H is called monotone if for all x, y ∈ H, f ∈ Tx and g ∈ Ty imply 〈x - y, f - g〉 ≥ 0. A monotone mapping T : H → 2 ^H is maximal if its graph G(T) is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping T is maximal if and only if for (x, f) ∈ H × H, 〈x - y, f - g〉 ≥ 0 for all (y, g) ∈ G(T) implies f ∈ Tx. Let A : C → H be a monotone, L-Lipschitz continuous mapping and let N _C v be the normal cone to C at v ∈ C, i.e., N _C v = {w ∈ H : 〈v - u, w〉 ≥ 0, ∀u ∈ C}. Define

It is known that in this case T is maximal monotone, and 0 ∈ Tv if and only if v ∈ Ω; see [33].

3. Extragradient-like approximation method and strong convergence results

Let A : C → H be a monotone and L-Lipschitz continuous mapping, f : C → C be a contraction with contractive constant α ∈ (0, 1) and S : C → C be an asymptotically κ-strict pseudocontractive mapping in the intermediate sense with sequence {γ _n }. In this paper, we introduce an extragradient-like iterative algorithm that is based on the extragradient-like approximation method in [11] and the modified Mann iteration process in [20]:

(3.1)

where {λ _n } is a sequence in (0, 1) with , and {α _n }, {β _n }, {μ _n } and {ν _n } are sequences in [0, 1] satisfying the following conditions:

(A1) α _n + β _n + ν _n ≤ 1 for all n ≥ 1;

(A2) lim_n→∞α _n = 0, ;

(A3) κ < lim inf_n→∞β _n ≤ lim sup_n→∞β _n < 1;

(A4) .

The following result shows the strong convergence of the sequences {x _n }, {y _n } generated by the scheme (3.1) to the same point q = P_F(S)∩Ωf (q) if and only if {Ax _n } is bounded, ||(I - Sⁿ )x _n || → 0 and lim inf_n→∞〈Ax _n , y - x _n 〉 ≥ 0 for all y ∈ C.

Theorem 3.1. Let A : C → H be a monotone and L-Lipschitz continuous mapping, f : C → C be a contraction with contractive constant α ∈ (0, 1) and S : C → C be a uniformly continuous asymptotically κ-strict pseudocontractive mapping in the intermediate sense with sequence {γ _n } such that F(S) ∩ Ω ≠ ∅ and. Let {x _n }, {y _n } be the sequences generated by (3.1), where {λ _n } is a sequence in (0, 1) with, and {α _n }, {β _n }, {μ _n } and{y _n } are sequences in [0, 1] satisfying the conditions (A1)-(A4). Then, the sequences {x _n }, {y _n } converge strongly to the same point q = P_F(S)∩Ωf (q) if and only if {Ax _n } is bounded, ||(I - Sⁿ )x _n || → 0 and lim inf_n→∞〈Ax _n , y - x _n 〉 ≥ 0 for all y ∈ C.

Proof. "Necessity". Suppose that the sequences {x _n }, {y _n } converge strongly to the same point q = P_F(S)∩Ωf (q). Then from the L-Lipschitz continuity of A, it follows that {Ax _n } is bounded, and for each y ∈ C:

which implies that

due to q ∈ Ω. Furthermore, utilizing Lemma 2.3, we have

due to x _n → q, γ _n → 0 and c _n → 0. Consequently, we conclude that for each y ∈ C

That is, ||(I - Sⁿ )x _n || → 0.

"Sufficiency". Suppose that {Ax _n } is bounded, ||(I - Sⁿ )x _n || → 0 and lim inf_n→∞〈Ax _n , y - x _n 〉 ≥ 0 for all y ∈ C. Note that lim inf_n→∞β _n > κ. Hence, we may assume, without loss of generality, that β _n > κ for all n ≥ 1.

Next, we divide the proof of the sufficiency into several steps.

STEP 1. We claim that {x _n } is bounded. Indeed, put t _n = P _C (x _n - λ _n Ay _n ) for all n ≥ 1. Let x* ∈ F(S) ∩ Ω. Then, x* = P _C (x* - λ _n Ax*). Putting x = x _n - λ _n Ay _n and y = x* in (2.5), we obtain

(3.2)

Since A is monotone and x* is a solution of VIP(A, C), we have

It follows from (3.2) that

(3.3)

Note that x _n ∈ C for all n ≥ 1 and that y _n = (1 - μ _n )x _n + μ _n P _C (x _n - λ _n Ax _n ). Hence, we have

(3.4)

Since {Ax _n } is bounded and A is L-Lipschitz continuous, we have

and hence ||Ay _n || ≤ (1+ L)||Ax _n ||, which implies that {Ay _n } is bounded. Hence, we may assume that there exists a constant M ≥ sup{||Ax _n || + ||Ay _n || + ||Ax*||: n ≥ 1}. Then, it follows from (3.4) that

This together with (3.3) implies that

(3.5)

Observe that

(3.6)

Putting τ _n = α _n + β _n + ν _n and utilizing Lemma 2.5, we obtain from (3.5) and (3.6)

(3.7)

Now, let us show that for all n ≥ 1

(3.8)

As a matter of fact, whenever n = 1, from (3.7), we have

Assume that (3.8) holds for some n ≥ 1. Consider the case of n + 1. From (3.7), we obtain

This shows that (3.8) holds for the case of n + 1. By induction, we know that (3.8) holds for all n ≥ 1. Since , and , from (3.8) we deduce that for all n ≥ 1

This implies that {x _n } is bounded.

STEP 2. We claim that lim_n→∞||x_n+1- x _n || = 0. Indeed, observe that

(3.9)

and

(3.10)

Define a sequence {z _n } by

where ϱ _n = 1 - α _n - β _n - ν _n , ∀n ≥ 1. Then we have

(3.11)

From (3.9)-(3.11), we get

(3.12)

which implies that

Note that the boundedness of {x _n } implies that {f (x _n )} is also bounded. Since

(3.13)

we know that {y _n } is bounded and so is {f (y _n )}. Moreover, {t _n } is bounded by (3.5). Now, utilizing Lemma 2.3, we obtain that

Thus, from the boundedness of {t _n }, it follows that {Sⁿt _n } is bounded. Also, note that conditions

(ii), (iii) imply

and conditions (iii), (iv) lead to

Thus, we deduce from (3.12) that

Since ϱ _n = 1 - α _n - β _n - ν _n , we know from conditions (ii), (iii), (iv) that

Thus, in terms of Lemma 2.7, we get lim_n→∞||z _n - x _n || = 0. Consequently,

(3.14)

STEP 3. We claim that lim_n→∞||Sx _n - x _n || = lim_n→∞||St _n - t _n || = 0. Indeed, observe that

and hence

Note that the following condition holds:

(3.15)

Also, observe that

(3.16)

Utilizing Lemma 2.3 and t _n - x _n → 0, we have

(3.17)

Thus from (3.15)-(3.17), we obtain

(3.18)

In addition, from (3.9) and x_n+1- x_{n → 0}, it follows that t_n+1- t_{n → 0}. Therefore, utilizing the uniform continuity of S and Lemma 2.4, we know that lim_n→∞||Sx _n - x _n || = 0 and lim_n→∞||St _n - t _n || = 0.

STEP 4. We claim that lim sup_n→∞〈f (q) - q, x _n - q〉 ≤ 0. Indeed, we pick a subsequence of {x _n } so that

(3.19)

Without loss of generality, let . Then, (3.19) reduces to

In order to show , it suffices to show that . Since S is uniformly continuous and ||x _n - Sx _n || → 0, we see that ||x _n - S^mx _n || → 0 for all m ≥ 1. By Proposition 2.1, we obtain . Now let us show that . Let

Then, T is maximal monotone and 0 ∈ Tv if and only if v ∈ Ω; see [33]. Let (v, w) ∈ G(T). Then, we have w ∈ Tv = Av + N _C v and hence w - Av ∈ N _C v. Therefore, we have 〈v - u, w - Av〉 ≥ 0 for all u ∈ C. In particular, taking , we get

and so . Since T is maximal monotone, we have and hence .

This shows that . Therefore by the property of the metric projection, we derive .

STEP 5. We claim that lim_n→∞||x _n - q|| = 0 where q = P_F(S)∩Ωf (q). Indeed, since {Ax _n }, {Ay _n }, {Sⁿt _n } are bounded, we may assume that there exists a constant M ≥ sup{||Ax _n || +||Ay _n || + ||Aq|| + ||Sⁿt _n - q||: n ≥ 1 g. Then from (3.1), (3.5) and Lemma 2.8, we get

which implies that

(3.20)

Note that lim_n→∞α _n = 0 and . Since lim sup_n→∞〈f (q) - q, x_n+1- q〉 ≤ 0, lim_n→∞||y _n - x _n || = 0 and {x _n - q} is bounded, we know that

Also, since and , it is easy to see that

Therefore, according to Lemma 2.6, we deduce that from (3.20) that ||x _n - q|| → 0. Further from ||y _n - x _n || → 0, we obtain ||y _n - q|| → 0. This completes the proof. □

In Theorem 3.1, if we put ν _n = 0 (∀n ≥ 1) and S = I the identity mapping. Then, the iterative scheme (3.1) reduces to the following scheme:

(3.21)

Moreover, it is easy to see that and ||(1 - Sⁿ )x _n || → 0. Thus, we have following corollary.

Corollary 3.1. Let A : C → H be a monotone, L-Lipschitz continuous mapping, and f : C → C be a contraction with contractive constant α ∈ (0, 1). Let Ω ≠ ∅. Let {x _n }, {y _n } be the sequences generated by (3.21), where {λ _n } is a sequence in (0, 1) with, and {α _n }, {β _n } and {μ _n } are three sequences in [0, 1] satisfying the conditions:

(B1) α _n + β _n ≤ 1 for all n ≥ 1,

(B2) lim_n→∞α _n = 0, ;

(B3) 0 < lim inf_n→∞β _n ≤ lim sup_n→∞β _n < 1.

Then, the sequences {x _n }, {y _n } converge strongly to the same point q = P_Ωf (q) if and only if {Ax _n } is bounded and lim inf_n→∞〈Ax _n , y - x _n 〉 ≥ 0 for all y ∈ C.

If A^-10 = Ω and P _H = I, the identity mapping of H, then the iterative scheme (3.1) reduces to the following iterative scheme:

(3.22)

The following corollary can be easily derived from Theorem 3.1.

Corollary 3.2. Let f : H → H be a contractive mapping with constant α ∈ (0, 1), A : H → H be a monotone, L-Lipschitz continuous mapping and S : H → H be a uniformly continuous asymptotically κ-strict pseudocontractive mapping in the intermediate sense with sequence {γ _n } such that F(S) ∩ A^{- 1}0 ≠ ∅ and. Let {x _n }, {y _n } be the sequences generated by (3.22), where {λ _n } is a sequence in (0, 1) with, and {α _n }, {β _n }, {μ _n } and {ν _n } are four sequences in [0, 1] satisfying the conditions (A1)-(A4). Then, the sequences {x _n }, {y _n } converge strongly to the same pointif and only if {Ax _n } is bounded, ||(I - Sⁿ )x _n || → 0 and lim inf_n→∞〈Ax _n , y - x _n 〉 ≥ 0 for all y ∈ H.

Let B : H → 2 ^H be a maximal monotone mapping. Then, for any x ∈ H and r > 0, consider . Such is called the resolvent of B and is denoted by .

If we put and P _H = I, then the iterative scheme (3.1) reduces to the following scheme:

(3.23)

It is easy to see that κ = 0, γ _n = 0 and c _n = 0 for all n ≥ 1. Moreover, we have A^-10 = Ω and . Thus, utilizing Theorem 3.1, we obtain the following corollary.

Corollary 3.3. Let f : H → H be a contractive mapping with constant α ∈ (0, 1), A : H → H be a monotone, L-Lipschitz continuous mapping and B : H → 2 ^H be a maximal monotone mapping such that A^-10 ∩ B^-1 ≠ ∅. Letbe the resolvent of B for each r > 0. Let {x _n }, {y _n } be the sequences generated by (3.23), where {λ _n } is a sequence in (0, 1) with, and {α _n }, {β _n }, {μ _n } and {ν _n } are four sequences in [0, 1] satisfying the conditions (A1)-(A4). Then, the sequences {x _n }, {y _n } converge strongly to the same pointif and only if {Ax _n } is bounded,and lim inf_n→∞〈Ax _n , y - x _n 〉 ≥ 0 for all y ∈ H.

Corollary 3.4. Let f : H → H be a contractive mapping with constant α ∈ (0, 1) and A : H → H be a monotone, L-Lipschitz continuous mapping such that A^-10 ≠ ∅.Let {x _n }, {y _n } be the sequences generated by

(3.24)

where {λ _n } is a sequence in (0, 1) with, and {α _n }, {β _n } and {μ _n } are three sequences in [0, 1] satisfying the conditions (B1)-(B3). Then, the sequences {x _n }, {y _n } converge strongly to the same pointif and only if {Ax _n } is bounded and lim inf_n→∞〈Ax _n , y - x _n 〉 ≥ 0 for all y ∈ C.

Proof. In Theorem 3.1, put C = H, ν _n = 0 (∀n ≥ 1) and S = I the identity mapping of H. Then, we know that κ = 0, γ _n = 0 and c _n = 0 for all n ≥ 1. Moreover, we have A^-10 = Ω. PH = I. In this case, it is easy to see that and ||(I - Sⁿ )x _n || → 0. Therefore, by Theorem 3.1, we obtain the desired conclusion. □

We also know one more definition of a pseudocontractive mapping, which is equivalent to the definition given in the preliminaries. A mapping S : C → C is called pseudocontractive [26] if

Obviously, the class of pseudocontractive mappings is more general than the class of nonexpansive mappings. For the class of pseudocontractive mappings, there are some nontrivial examples; see, e.g., [[24], p. 1239] for further details. In the following theorem, we introduce an iterative process that converges strongly to a common fixed point of two mappings, one of which is an asymptotically κ-strict pseudocontractive mapping in the intermediate sense with sequence {γ _n } and the other Lipschitz continuous and pseudocontractive.

Theorem 3.2. Let f : C → C be a contractive mapping with constant α ∈ (0, 1), T : C → C be a pseudocontractive, m-Lipschitz continuous mapping and S : C → C be a uniformly continuous asymptotically κ-strict pseudocontractive mapping in the intermediate sense with sequence {γ _n } such that F(S) ∩ F(T) ≠ ∅ and. Let {x _n }, {y _n } be the sequences generated by

(3.25)

where A = I - T, {λ _n } is a sequence in (0, 1) with, and {α _n }, {β _n }, {μ _n } and {ν _n } are four sequences in [0, 1] satisfying the conditions (A1)-(A4). Then, the sequences {x _n }, {y _n } converge strongly to the same point q = P_F(S)∩F(T)f (q) if and only if {Ax _n } is bounded, ||(I - Sⁿ )x _n || → 0 and lim inf_n→∞〈Ax _n , y - x _n 〉 ≥ 0 for all y ∈ C.

Proof. Let A = I - T. Let us show that the mapping A is monotone and (m + 1)-Lipschitz continuous. Indeed, observe that

and

Now, let us show that F(T) = Ω. Indeed, we have, for fixed λ₀ ∈ (0, 1),

By Theorem 3.1, we obtain the desired conclusion. □

Theorem 3.3. Let f : C → C be a contractive mapping with constant α ∈ (0, 1), T : C → C be a pseudocontractive, m-Lipschitz continuous mapping and S : C → C be a nonexpansive mapping such that F(S) ∩ F(T) ≠ ∅. Let {x _n }, {y _n } be the sequences generated by

(3.26)

where A = I - T, {λ _n } is a sequence in (0, 1) with, and {α _n }, {β _n }, {μ _n } and {ν _n }

are sequences in [0, 1] satisfying the conditions (A1)-(A4). Then, the sequences {x _n }, {y _n } converge strongly to the same point q = P_F(S)∩F(T)f (q) if and only if {Ax _n } is bounded, ||(I - Sⁿ )x _n || → 0 and lim inf_n→∞〈Ax _n , y - x _n 〉 ≥ 0 for all y ∈ C.

Proof. Let A = I - T. In terms of the proof of Theorem 3.2, we know that A is a monotone and (m+1)-Lipschitz continuous mapping such that F(T) = Ω. Since S is a nonexpansive mapping, we know that κ = 0, γ _n = 0 and c _n = 0 for all n ≥ 1. By Theorem 3.1, we obtain the desired conclusion. □