- Research
- Open access
- Published:
Fixed point results for contractions involving generalized altering distances in ordered metric spaces
Fixed Point Theory and Applications volume 2011, Article number: 5 (2011)
Abstract
In this article, we establish coincidence point and common fixed point theorems for mappings satisfying a contractive inequality which involves two generalized altering distance functions in ordered complete metric spaces. As application, we study the existence of a common solution to a system of integral equations.
2000 Mathematics subject classification. Primary 47H10, Secondary 54H25
Introduction and Preliminaries
There are a lot of generalizations of the Banach contraction-mapping principle in the literature (see [1–31] and others).
A new category of contractive fixed point problems was addressed by Khan et al. [1]. In this study, they introduced the notion of an altering distance function which is a control function that alters distance between two points in a metric space.
Definition 1.1. [1] A function φ: [0, +∞) → [0, +∞) is called an altering distance function if the following conditions are satisfied.
-
(i)
φ is continuous.
-
(ii)
φ is non-decreasing.
-
(iii)
φ (t) = 0 ⇔ t = 0.
Khan et al. [1] proved the following result:
Theorem 1.2. [1]Let (X, d) be a complete metric space, φ: [0, +∞) → [0, +∞) be an altering distance function, and T : X → X be a self-mapping which satisfies the following inequality:

for all x, y ∈ X and for some 0 < c < 1. Then, T has a unique fixed point.
Letting φ(t) = t in Theorem 1.2, we retrieve immediately the Banach contraction principle.
In 1997, Alber and Guerre-Delabriere [2] introduced the concept of weak contractions in Hilbert spaces. This concept was extended to metric spaces in [3].
Definition 1.3. Let (X, d) be a metric space. A mapping T : X → X is said to be weakly contractive if

where φ: [0, +∞) → [0, +∞) is an altering distance function.
Theorem 1.4. [3]Let (X, d) be a complete metric space and T : X → X be a weakly contractive map. Then, T has a unique fixed point.
Weak inequalities of the above type have been used to establish fixed point results in a number of subsequent studies, some of which are noted in [4–7]. In [5], Choudhury introduced the concept of a generalized altering distance function.
Definition 1.5. [5] A function φ: [0, +∞) × [0, +∞) × [0, +∞) → [0, +∞) is said to be a generalized altering distance function if the following conditions are satisfied:
-
(i)
φ is continuous.
-
(ii)
φ is non-decreasing in all the three variables.
-
(iii)
φ (x, y, z) = 0 ⇔ x = y = z = 0.
In [5], Choudhury proved the following common fixed point theorem:
Theorem 1.6. [5]Let (X, d) be a complete metric space and S, T : X → X be two self-mappings such that the following inequality is satisfied:

for all x, y ∈ X, where ψ1and ψ2are generalised altering distance functions, and Φ1(x) = ψ1(x, x, x). Then, S and T have a common fixed point.
Recently, there have been so many exciting developments in the field of existence of fixed point in partially ordered sets (see [8–27] and the references cited therein). The first result in this direction was given by Turinici [27], where he extended the Banach contraction principle in partially ordered sets. Ran and Reurings [24] presented some applications of Turinici's theorem to matrix equations. The obtained result by Turinici was further extended and refined in [20–23].
In this article, we obtain coincidence point and common fixed point theorems in complete ordered metric spaces for mappings, satisfying a contractive condition which involves two generalized altering distance functions. Presented theorems are the extensions of Theorem 1.6 of Choudhury [5]. In addition, as an application, we study the existence of a common solution for a system of integral equations.
Main Results
At first, we introduce some notations and definitions that will be used later. The following definition was introduced by Jungck [28].
Definition 2.1. [28] Let (X, d) be a metric space and f, g : X → X. If w = fx = gx, for some x ∈ X, then x is called a coincidence point of f and g, and w is called a point of coincidence of f and g. The pair {f, g} is said to be compatible if and only if  , whenever {x
n
} is a sequence in X such that
, whenever {x
n
} is a sequence in X such that  for some t ∈ X.
for some t ∈ X.
Let X be a nonempty set and R : X → X be a given mapping. For every x ∈ X, we denote by R-1(x) the subset of X defined by

In [19], Nashine and Samet introduced the following concept:
Definition 2.2. [19] Let (X, ≤) be a partially ordered set, and T, S, R : X → X are given mappings, such that TX ⊆ RX and SX ⊆ RX. We say that S and T are weakly increasing with respect to R if for all x ∈ X, we have

and

Remark 2.3. If R : X → X is the identity mapping (Rx = x for all x ∈ X), then S and T are weakly increasing with respect to R implies that S and T are weakly increasing mappings. It is noted that the notion of weakly increasing mappings was introduced in [9] (also see [16, 29]).
Example 2.4. Let X = [0, +∞) endowed with the usual order ≤. Define the mappings T, S, R : X → X by

and

Then, we will show that the mappings S and T are weakly increasing with respect to R.
Let x ∈ X. We distinguish the following two cases.
-
First case: x = 0 or x ≥ 1.
-
(i)
Let y ∈ R -1(Tx), that is, Ry = Tx. By the definition of T, we have Tx = 0 and then Ry = 0. By the definition of R, we have y = 0 or y ≥ 1. By the definition of S, in both cases, we have Sy = 0. Then, Tx = 0 = Sy.
-
(ii)
Let y ∈ R -1(Sx), that is, Ry = Sx. By the definition of S, we have Sx = 0, and then Ry = 0. By the definition of R, we have y = 0 or y ≥ 1. By the definition of T, in both cases, we have Ty = 0. Then, Sx = 0 = Ty.
-
Second case: 0 < x < 1.
-
(i)
Let y ∈ R -1(Tx), that is, Ry = Tx. By the definition of T, we have Tx = x and then Ry = x. By the definition of R, we have Ry = y 2, and then
 . We have
. We have 
-
(ii)
Let y ∈ R -1(Sx), that is, Ry = Sx. By the definition of S, we have
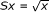 , and then
, and then 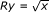 . By the definition of R, we have Ry = y 2, and then y = x 1/4. We have
. By the definition of R, we have Ry = y 2, and then y = x 1/4. We have 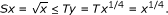
Thus, we proved that S and T are weakly increasing with respect to R.
Example 2.5. Let X = {1, 2, 3} endowed with the partial order ≤ given by

Define the mappings T, S, R : X → X by

We will show that the mappings S and T are weakly increasing with respect to R.
Let x, y ∈ X such that y ∈ R-1(Tx). By the definition of S, we have Sy = 1. On the other hand, Tx ∈ {1, 3} and (1, 1), (3, 1) ∈≤. Thus, we have Tx ≤ Sy for all y ∈ R-1(Tx).
Let x, y ∈ X such that y ∈ R-1(Sx). By the definitions of S and R, we have R-1(Sx) = R-1(1) = {1}. Then, we have y = 1. On the other hand, 1 = Sx ≤ Ty = T 1 = 1. Then, Sx ≤ Ty for all y ∈ R-1(Sx). Thus, we proved that S and T are weakly increasing with respect to R.
Our first result is as follows.
Theorem 2.6. Let (X, ≤) be a partially ordered set, and suppose that there exists a metric d on X such that (X, d) is a complete metric space. Let T, S, R : X → X be given mappings, satisfying for every pair (x, y) ∈ X × X such that Rx and Ry are comparable:

where ψ1and ψ2are generalized altering distance functions, and Φ1(x) = ψ1(x, x, x).
We assume the following hypotheses:
-
(i)
T, S, and R are continuous.
-
(ii)
TX ⊆ RX, SX ⊆ RX.
-
(iii)
T and S are weakly increasing with respect to R.
-
(iv)
the pairs {T, R} and {S, R} are compatible.
Then, T, S, and R have a coincidence point, that is, there exists u ∈ X such that Ru = Tu = Su.
Proof. Let x0 ∈ X be an arbitrary point. Since TX ⊆ RX, there exists x1 ∈ X such that Rx1 = Tx0. Since SX ⊆ RX, there exists x2 ∈ X such that Rx2 = Sx1.
Continuing this process, we can construct a sequence {Rx n } in X defined by

We claim that

To this aim, we will use the increasing property with respect to R for the mappings T and S. From (2.2), we have

Since Rx1 = Tx0, x1 ∈ R-1 (Tx0), and we get

Again,

Since x2 ∈ R-1 (Sx 1), we get

Hence, by induction, (2.3) holds.
Without loss of the generality, we can assume that

Now, we will prove our result on three steps.
Step I. We will prove that

Letting x = x2n+1and y = x2n, from (2.3) and the considered contraction, we have

Suppose that

Using the property of the generalized altering function, this implies that

Hence, we obtain

This implies that

and

Hence, we obtain a contradiction with (2.4). We deduce that

Similarly, letting x = x2n+1and y = x2n+2, from (2.3) and the considered contraction, we have

Suppose that

Then, from (2.9) and (2.10), we obtain

This implies that

and

Hence, we obtain a contradiction with (2.4). We deduce that

Combining (2.8) and (2.11), we obtain

Hence, {d(Rxn+1, Rxn+2)} is a decreasing sequence of positive real numbers. This implies that there exists r ≥ 0 such that

Define the function Φ2: [0, +∞) → [0, +∞) by

From (2.6) and (2.12), we obtain

which implies that

Similarly, from (2.9) and (2.12), we obtain

which implies that

Now, combining (2.14) and (2.15), we obtain

This implies that for all  , we have
, we have

This implies that

Hence,

Now, using (2.13), (2.16), and the continuity of Φ2, we obtain

which implies that r = 0. Hence, (2.5) is proved.
Step II. We claim that {Rx n } is a Cauchy sequence.
From (2.5), it will be sufficient to prove that {Rx2n} is a Cauchy sequence. We proceed by negation, and suppose that {Rx2n} is not a Cauchy sequence. Then, there exists ε > 0 for which we can find two sequences of positive integers {m(i)} and {n(i)} such that for all positive integer i,

From (2.17) and using the triangular inequality, we get

Letting i → +∞ in the above inequality, and using (2.5), we obtain

Again, the triangular inequality gives us

Letting i → +∞ in the above inequality, and using (2.5) and (2.18), we get

On the other hand, we have

Then, from (2.5), (2.18), and the continuity of Φ1, and letting i → +∞ in the above inequality, we have

Now, using the considered contractive condition for x = x2m(i)-1and y = x2n(i), we have

Then, from (2.5), (2.19), and the continuity of ψ1 and ψ2, and letting i → +∞ in the above inequality, we have

Now, combining (2.20) with the above inequality, we get

which implies that ψ2(ε, 0, 0) = 0, that is a contradiction since ε > 0. We deduce that {Rx n } is a Cauchy sequence.
Step III. Existence of a coincidence point.
Since {Rx n } is a Cauchy sequence in the complete metric space (X, d), there exists u ∈ X such that

From (2.21) and the continuity of R, we get

By the triangular inequality, we have

On the other hand, we have

Since R and T are compatible mappings, this implies that

Now, from the continuity of T and (2.21), we have

Combining (2.22), (2.24), and (2.25), and letting n → +∞ in (2.23), we obtain

that is,

Again, by the triangular inequality, we have

On the other hand, we have

Since R and S are compatible mappings, this implies that

Now, from the continuity of S and (2.21), we have

Combining (2.22), (2.28), and (2.29), and letting n → + ∞ in (2.27), we obtain

that is,

Finally, from (2.26) and (2.30), we have

that is, u is a coincidence point of T, S, and R. This completes the proof.
In the next theorem, we omit the continuity hypotheses on T, S, and R.
Definition 2.7. Let (X,≤, d) be a partially ordered metric space. We say that X is regular if the following hypothesis holds: if {z
n
} is a non-decreasing sequence in X with respect to ≤ such that z
n
→ z ∈ X as n → +∞, then z
n
≤ z for all 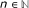 .
.
Now, our second result is the following.
Theorem 2.8. Let (X,≤) be a partially ordered set, and suppose that there exists a metric d on X such that (X, d) is a complete metric space. Let T, S, R : X → X be given mappings satisfying for every pair (x, y) ∈ X × X such that Rx and Ry are comparable,

where ψ1and ψ2are generalized altering distance functions and Φ1(x) = ψ1(x, x, x). We assume the following hypotheses:
-
(i)
X is regular.
-
(ii)
T and S are weakly increasing with respect to R.
-
(iii)
RX is a closed subset of (X, d).
-
(iv)
TX ⊆ RX, SX ⊆ R X.
Then, T, S, and R have a coincidence point.
Proof. From the proof of Theorem 2.6, we have that {Rx n } is a Cauchy sequence in (RX, d) which is complete, since RX is a closed subspace of (X, d). Hence, there exists u = Rv, v ∈ X such that

Since {Rx
n
} is a non-decreasing sequence and X is regular, it follows from (2.31) that Rx
n
≤ Rv for all  . Hence, we can apply the considered contractive condition. Then, for x = v and y = x2n, we obtain
. Hence, we can apply the considered contractive condition. Then, for x = v and y = x2n, we obtain

Letting n → +∞ in the above inequality, and using (2.5), (2.31), and the properties of ψ1 and ψ2, then we have

This implies that ψ2(0, d(Rv, Sv), 0) = 0, which gives us that d(Rv, Sv) = 0, i.e.,

Similarly, for x = x2n+1and y = v, we obtain

Letting n → +∞ in the above inequality, we get

This implies that ψ2(0, 0, d(Rv, Tv)) = 0 and then,

Now, combining (2.32) and (2.33), we obtain

Hence, v is a coincidence point of T, S, and R. This completes the proof.
Now, we present an example to illustrate the obtained result given by the previous theorem. Moreover, in this example, we will show that Theorem 1.6 of Choudhury cannot be applied.
Example 2.9. Let X = {4, 5, 6} endowed with the usual metric d(x, y) = |x - y| for all x, y ∈ X, and ≤:= {(4, 4), (5, 5), (6, 6), (6, 4)}. Clearly, ≤ is a partial order on X. Consider the mappings T, S, R : X → X defined by

We will show that T and S are weakly increasing with respect to R. In the case under study, we have to check that Tx ≤ T(Tx) for all x ∈ X.
For x = 4, we have

For x = 5, we have

For x = 6, we have

Thus, we have proved that T and S are weakly increasing with respect to R.
Now, we will show that (X, ≤, d) is regular.
Let {z
n
} be a non-decreasing sequence in X with respect to ≤ such that z
n
→ z ∈ X as n → +∞. Then, we have z
n
≤ zn+1, for all 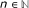 .
.
-
If z0 = 4, then z0 = 4 ≤ z1. From the definition of ≤, we have z1 = 4. By induction, we get z n = 4 for all
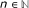 and z = 4. Then, z
n
≤ z for all
and z = 4. Then, z
n
≤ z for all 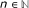 .
. -
If z0 = 5, then z0 = 5 ≤ z1. From the definition of ≤, we have z1 = 5. By induction, we get z n = 5 for all
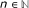 and z = 5. Then, z
n
≤ z for all
and z = 5. Then, z
n
≤ z for all 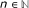 .
. -
If z0 = 6, then z0 = 6 ≤ z1. From the definition of ≤, we have z1 ∈ {6, 4}. By induction, we get z n ∈ {6, 4} for all
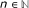 . Suppose that there exists p ≥ 1 such that z
p
= 4. From the definition of ≤, we get z
n
= z
p
= 4 for all n ≥ p. Thus, we have z = 4 and z
n
≤ z for all
. Suppose that there exists p ≥ 1 such that z
p
= 4. From the definition of ≤, we get z
n
= z
p
= 4 for all n ≥ p. Thus, we have z = 4 and z
n
≤ z for all 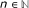 . Now, suppose that z
n
= 6 for all
. Now, suppose that z
n
= 6 for all 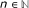 . In this case, we get z = 6, and z
n
≤ z for all
. In this case, we get z = 6, and z
n
≤ z for all 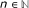 . Thus, we proved that in all the cases considered, we have z
n
≤ z for all
. Thus, we proved that in all the cases considered, we have z
n
≤ z for all 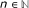 . Then, (X, ≤, d) is regular.
. Then, (X, ≤, d) is regular.
Now, define the functions ψ1, ψ2 : [0, +∞) × [0, +∞) × [0, +∞) → [0, +∞) by

and

Clearly, ψ1 and ψ2 are the generalized altering distance functions, and for every x, y ∈ X such that Rx ≤ Ry, inequality (2.1) is satisfied.
Now, we can apply Theorem 2.8 to deduce that T, S, and R have a coincidence point u = 4. Note that u is also a fixed point of T since S = T, and R is the identity mapping.
On the other hand, taking x = 4 and y = 5, we get

Thus, Inequality (1.2) is not satisfied for x = 4 and y = 5. Then, Theorem 1.6 of Choudhury [5] cannot be applied in this case.
If R : X → X is the identity mapping, we can deduce easily the following common fixed point results.
The next result is an immediate consequence of Theorem 2.6.
Corollary 2.10. Let (X, ≤) be a partially ordered set, and suppose that there exists a metric d on X such that (X, d) is a complete metric space. Let T, S : X → X be given mappings satisfying for every pair (x, y) ∈ X × X such that x and y are comparable. Then,

where ψ1and ψ2are generalized altering distance functions and Φ1(x) = ψ1(x, x, x). We assume the following hypotheses:
-
(i)
T and S are continuous.
-
(ii)
T and S are weakly increasing.
Then, T and S have a common fixed point, that is, there exists u ∈ X such that u = Tu = Su.
The following result is an immediate consequence of Theorem 2.8.
Corollary 2.11. Let (X, ≤) be a partially ordered set and suppose that there exists a metric d on X such that (X, d) is a complete metric space. Let T, S : X → X be given mappings satisfying for every pair (x, y) ∈ X × X such that x and y are comparable. Then,

where ψ1and ψ2are generalised altering distance functions and Φ1(x) = ψ1(x, x, x). We assume the following hypotheses:
-
(i)
X is regular.
-
(ii)
T and S are weakly increasing.
Then, T and S have a common fixed point.
A number of fixed point results may be obtained by assuming different forms for the functions ψ1 and ψ2. In particular, fixed point results under various contractive conditions may be derived from the above theorems. For example, if we consider

where s > 0 and 0 < k = k1 + k2 + k3< 1, then we obtain the following results.
The next result is an immediate consequence of Corollary 2.10.
Corollary 2.12. Let (X, ≤) be a partially ordered set, and suppose that there exists a metric d on X such that (X, d) is a complete metric space. Let T, S : X → X be given mappings satisfying for every pair (x, y) ∈ X × X such that x and y are comparable. Then,

where s > 0 and 0 < k = k1 + k2 + k3< 1. We assume the following hypotheses:
-
(i)
T and S are continuous.
-
(ii)
T and S are weakly increasing.
Then, T and S have a common fixed point, that is, there exists u ∈ X such that u = Tu = Su.
The next result is an immediate consequence of Corollary 2.11.
Corollary 2.13. Let (X, ≤) be a partially ordered set, and suppose that there exists a metric d on X such that (X, d) is a complete metric space. Let T, S : X → X be given mappings satisfying for every pair (x, y) ∈ X × X such that x and y are comparable. Then,

where s > 0 and 0 < k = k1 + k2 + k3< 1. We assume the following hypotheses:
-
(i)
X is regular.
-
(ii)
T and S are weakly increasing.
Then, T and S have a common fixed point.
Remark 2.14. Other fixed point results may also be obtained under specific choices of ψ1 and ψ2.
Application
Consider the integral equations:

where T > 0.
The purpose of this section is to give an existence theorem for common solution of (3.1) using Corollary 2.13. This application is inspired in [9].
Previously, we have considered the space C(I)(I = [0, T]) of continuous functions defined on I. Obviously, this space with the metric given by

is a complete metric space. C(I) can also be equipped with the partial order ≤ given by

Moreover, in [20], it is proved that (C(I), ≤) is regular.
Now, we will prove the following result.
Theorem 3.1. Suppose that the following hypotheses hold:
-
(i)
K 1, K 2 : I × I × ℝ → ℝ, and g : ℝ → ℝ are continuous;
-
(ii)
for all t, s ∈ I, we have
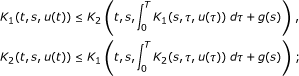
-
(iii)
there exists a continuous function p : I × I → ℝ+ such that
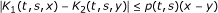
for all t, s ∈ I and x, y ∈ ℝ such that x ≥ y;
-
(iv)
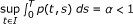 .
.
Then, the integral equations (3.1) have a solution u* ∈ C(I).
Proof. Define T, S : C(I) → C(I) by

and

Now, we will prove that T and S are weakly increasing. From (ii), for all t ∈ I, we have

Similarly,

Then, we have Tx ≤ STx and Sx ≤ TSx for all x ∈ C(I). This implies that T and S are weakly increasing.
Now, for all x, y ∈ C(I) such that x ≤ y, by (iii) and (iv), we have

This implies that for all x, y ∈ C(I) such that x ≤ y,

Hence, the contractive condition required by Corollary 2.13 is satisfied with s = 1, k1 = α, and k2 = k3 = 0.
Now, all the required hypotheses of Corollary 2.13 are satisfied. Then, there exists u* ∈ C(I), a common fixed point of T and S, that is, u* is a solution to (3.1).
References
Khan MS, Swaleh M, Sessa S: Fixed point theorems by altering distances between the points. Bull Aust Math Soc 1984, 30: 1–9. 10.1017/S0004972700001659
Alber YaI, Guerre-Delabriere S: Principles of weakly contractive maps in Hilbert spaces. Oper Theory Adv Appl 1997, 98: 7–22.
Rhoades BE: Some theorems on weakly contractive maps. Nonlinear Anal 2001, 47: 2683–2693. 10.1016/S0362-546X(01)00388-1
Abbas M, Ali Khan M: Common fixed point theorem of two mappings satisfying a generalized weak contractive condition. Int J Math Math Sci 2009, 2009: 9. Article ID 131068
Choudhury BS: A common unique fixed point result in metric spaces involving generalized altering distances. Math Commun 2005, 10: 105–110.
Dutta PN, Choudhury BS: A generalisation of contraction principle in metric spaces. Fixed Point Theory Appl 2008, 2008: 8. Article ID 406368
Zhang Q, Song Y: Fixed point theory for generalized φ-weakly contraction. Appl Math Lett 2009, 22: 75–78. 10.1016/j.aml.2008.02.007
Agarwal RP, El-Gebeily MA, O'Regan D: Generalized contractions in partially ordered metric spaces. Appl Anal 2008, 87: 109–116. 10.1080/00036810701556151
Altun I, Simsek H: Some fixed point theorems on ordered metric spaces and application. Fixed Point Theory Appl 2010, 2010: 17. Article ID 621492
Amini-Harandi A, Emami H: A fixed point theorem for contraction type maps in partially ordered metric spaces and application to ordinary differential equations. Nonlinear Anal 2010, 72: 2238–2242. 10.1016/j.na.2009.10.023
Beg I, Butt AR: Fixed point for set-valued mappings satisfying an implicit relation in partially ordered metric spaces. Nonlinear Anal 2009, 71: 3699–3704. 10.1016/j.na.2009.02.027
Beg I, Butt AR: Fixed points for weakly compatible mappings satisfying an implicit relation in partially ordered metric spaces. Carpathian J Math 2009, 25: 1–12.
Bhaskar TG, Lakshmikantham V: Fixed point theorems in partially ordered metric spaces and applications. Nonlinear Anal 2006, 65: 1379–1393. 10.1016/j.na.2005.10.017
Ćirić N, Cakić Lj, Rajović M, Ume JS: Monotone generalized nonlinear contractions in partially ordered metric spaces. Fixed Point Theory Appl 2008, 2008: 11. Article ID 131294
Lakshmikantham V, Ćirić Lj: Coupled fixed point theorems for nonlinear contractions in partially ordered metric spaces. Nonlinear Anal 2009, 70: 4341–4349. 10.1016/j.na.2008.09.020
Dhage BC, O'Regan D, Agrawal RP: Common fixed point theorems for a pair of countably condensing mappings in ordered Banach spaces. J Appl Math Stoch Anal 2003, 16: 243–248. 10.1155/S1048953303000182
Harjani J, Sadarangani K: Fixed point theorems for weakly contractive mappings in partially ordered sets. Nonlinear Anal 2009, 71: 3403–3410. 10.1016/j.na.2009.01.240
Harjani J, Sadarangani K: Generalized contractions in partially ordered metric spaces and applications to ordianry differential equations. Nonlinear Anal 2010, 72: 1188–1197. 10.1016/j.na.2009.08.003
Nashine HK, Samet B: Fixed point results for mappings satisfying ( ψ , φ )-weakly contractive condition in partially ordered metric spaces. Nonlinear Anal 2011, 74: 2201–2209. 10.1016/j.na.2010.11.024
Nieto JJ, Rodríguez-López R: Contractive mapping theorems in partially ordered sets and applications to ordianry differential equations. Order 2005, 22: 223–239. 10.1007/s11083-005-9018-5
Nieto JJ, Rodríguez-López R: Existence and uniqueness of fixed point in partially ordered sets and applications to ordianry differential equations. Acta Math Sinica (English Series) 2007,23(12):2205–2212. 10.1007/s10114-005-0769-0
Nieto JJ, Pouso RL, Rodríguez-López R: Fixed point theorems in ordered abstract spaces. Proc Am Math Soc 2007, 135: 2505–2517. 10.1090/S0002-9939-07-08729-1
O'Regan D, Petrusel A: Fixed point theorems for generalized contractions in ordered metric spaces. J Math Anal Appl 2008, 341: 1241–1252. 10.1016/j.jmaa.2007.11.026
Ran ACM, Reurings MCB: A fixed point theorem in partially ordered sets and some applications to matrix equations. Proc Am Math Soc 2004,132(5):1435–1443. 10.1090/S0002-9939-03-07220-4
Samet B: Coupled fixed point theorems for a generalized Meir-Keeler contraction in partially ordered metric spaces. Nonlinear Anal 2010, 72: 4508–4517. 10.1016/j.na.2010.02.026
Samet B, Yazidi H: Coupled fixed point theorems in partially ordered ε -chainable metric spaces. J Math Comput Sci 2010,1(3):142–151.
Turinici M: Abstract comparison principles and multivariable Gronwall-Bellman inequalities. J Math Anal Appl 1986, 117: 100–127. 10.1016/0022-247X(86)90251-9
Jungck G: Compatible mappings and common fixed points. Int J Math Math Sci 1986, 9: 771–779. 10.1155/S0161171286000935
Dhage BC: Condensing mappings and applications to existence theorems for common solution of differential equations. Bull Korean Math Soc 1999,36(3):565–578.
Boyd DW, Wong JSW: On nonlinear contractions. Proc Am Math Soc 1969, 20: 458–464. 10.1090/S0002-9939-1969-0239559-9
Reich S: Some fixed point problems. Atti Acad Naz Linei 1974, 57: 194–198.
Acknowledgements
The authors thank the referees for their valuable comments and suggestions. This work was supported by the Kyungnam University Research Fund, 2010.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that we have no competing interests.
Authors' contributions
JKK and HKN conceived the study and participated in its design and coordination. JKK suggested many good ideas that are useful for achievement this paper and made the revision. HKN and BS prepared the manuscript initially and performed all the steps of proof in this research. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Nashine, H.K., Samet, B. & Kim, J.K. Fixed point results for contractions involving generalized altering distances in ordered metric spaces. Fixed Point Theory Appl 2011, 5 (2011). https://doi.org/10.1186/1687-1812-2011-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-5
 . We have
. We have 
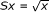 , and then
, and then 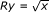 . By the definition of R, we have Ry = y 2, and then y = x 1/4. We have
. By the definition of R, we have Ry = y 2, and then y = x 1/4. We have 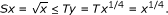
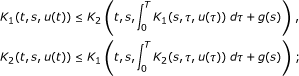
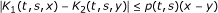
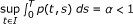 .
.