- Research
- Open access
- Published:
Convolution identities for twisted Eisenstein series and twisted divisor functions
Fixed Point Theory and Applications volume 2013, Article number: 81 (2013)
Abstract
We are motivated by Ramanujan’s recursion formula for sums of the product of two Eisenstein series (Berndt in Ramanujan’s Notebook, Part II, 1989, Entry 14, p.332) and its proof, and also by Besge-Liouville’s convolution identity for the ordinary divisor function (Williams in Number Theory in the Spirit of Liouville, vol. 76, 2011, Theorem 12.3). The objective of this paper is to introduce and prove convolution identities for the twisted divisor functions as well as for the twisted Eisenstein series and , , , and . As applications based on our main results, we establish many interesting identities for pyramidal, triangular, Mersenne, and perfect numbers. Moreover, we show how our main results can be used to obtain arithmetical formulas for the number of representations of an integer n as the sums of s squares.
1 Introduction and statement of main results
Throughout this paper, let be the complex upper half-plane. Let denote the normalized Eisenstein series of weight k defined on ℌ by
where , , and is the k th Bernoulli number.
Let , , and be the twisted Eisenstein series defined by
For , we define the twisted Eisenstein series by
where is the twisted divisor function given by
Consider the differential operator such that
We are motivated by Ramanujan’s recursion formula for [[1], Entry 14, p.332] and its proof, and also by Besge-Liouville’s convolution identity for the divisor function [[2], Theorem 12.3]. Inspired by these identities, we prove new identities for the convolution sums of various divisor functions , as well as recursion formulas for the twisted Eisenstein series , , and . Several arithmetical applications based on our results are given.
The problem of convolution sums of the divisor function and the theory of Eisenstein series has recently attracted considerable interest with the emergence of quasimodular tools. For further details, we can refer to the works of Royer [3], Ramakrishnan and Sahu [4], and Alaca and Williams [5, 6], and the references therein. In connection with the classical Jacobi theta and Euler functions, other aspects of the function are explored by Adiga in [7] and by Simsek in [8]. In this paper, we prove the following results. First, we state the most important identities for the convolution sums of divisor functions as follows.
Theorem 1.1 Let and , where . We have the identities in Table 1.
Our next results follow from the identities in Theorem 1.1. Thus, we obtain the following identities for the Eisenstein series.
Theorem 1.2 Let and , where . We have the identities in Table 2.
Let p be a prime number, and let l be any positive integer. We introduce the twisted divisor function

We define
In Section 3.2 , we establish the following less definitive result.
Theorem 1.3 Let and .
Finally, in the last Section 4, we show how to apply our main results to study some questions related to the famous problem
and its variants. Moreover, we consider similar questions on the arithmetic function . Many remarks and results are established.
2 The th scalar multiplicative function
Let p be a prime number, and let i be a nonnegative integer. A function is called a th scalar function if for all integers x.
Moreover, a th scalar function is called a th scalar multiplicative function if and only if for all positive integers x, y such that .
Example 2.1
-
1.
Let . Then is a p th scalar multiplicative function.
-
2.
Let s be a nonnegative integer; we recall that
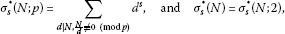
and we define the function
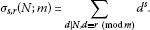
Then the function is a th scalar multiplicative function.
-
3.
The function is a 20th scalar multiplicative function.
Theorem 2.2 The divisor function is a th scalar multiplicative function.
Proof Let and  for some and prime p. Since l does not divide p, we can write for some . Therefore, we have
for some and prime p. Since l does not divide p, we can write for some . Therefore, we have

We claim that , where . If , then
Assume that and and . Hence, we have
Therefore . Then we get the theorem. □
Proposition 2.3 Let . For nonnegative integers m and n, we have
Proof
We can see that
Then, by Theorem 2.2, we have
Thus, using (8), we can write (7) as
□
3 Convolution relations on twisted Eisenstein series and their applications
3.1 Convolution relations on the twisted Eisenstein series
We quote the following lemma from [[2], Chap. 10, p.113].
Lemma 3.1 Let be an even function. Let . Then
Using the above lemma, we can prove our next result.
Theorem 3.2 Let . Then
Proof We take in Lemma 3.1. The left-hand side of Lemma 3.1 is
Therefore, we deduce that
From (10) and (2), we get the theorem. □
3.2 Proof of Theorem 1.3
From (4) and (10), we obtain
Then, the first term on the right-hand side of (11) can be written as
Similarly, the second term on the right-hand side of (11) is
Therefore, the proof is completed.
3.3 Pyramidal numbers
Let α be a fixed integer with , and let
denote the α th order pyramid number [9]. These combinatorial numbers play an important role in number theory and discrete mathematics. Using (10) with , we derive
Proposition 2.3 is a very efficient formula for the computation of the sum
For example, using Proposition 2.3 and (12), we get the interesting formulas in Table 3.
-
1.
The pyramidal numbers are closely connected to the convolution sums
In fact, if is a prime number, then from (12), we obtain
From Theorem 2.2, we deduce that
(13)where
In Table 4, we list the first thirteen values of
According to Table 4 and Figure 1, we observe that if is prime, then coincides with .
-
2.
We consider the pyramidal numbers
and the convolution sums
From (21) (with prime), we obtain
We list the first thirteen values of and in Table 5. According to Table 5 and Figure 2, we observe that if is prime, then coincides with . We note that
is an elliptic curve with and . From the Lutz-Nagell theorem [[10], p.240], P cannot be of finite order. For more details on the extended results of pyramidal numbers and rank of elliptic curves, one can refer to [9] .
3.4 Convolution on the twisted Eisenstein series ,
We prove the following result.
Lemma 3.3 Let . Then
and
Proof Let us put in (10). Then
From Theorem 2.2 and (14), we derive
From (14) and (15), we find that
From (15) and (16), we deduce our lemma. □
We have the following theorem.
Theorem 3.4 Let L, M, k be positive integers. Let
-
(a)
If , then
-
(b)
If with odd distinct primes , then
Proof
-
(a)
Since , we can choose and . From the definition of and (15), we obtain
-
(b)
Since with odd distinct primes , we have
□
3.5 Triangular and twisted triangular numbers: results and remarks
-
(1)
Using the theory of elliptic theta functions, Glaisher [[11], p.300] considered Eq. (15).
-
(2)
Four special cases for (15) and (16) are of interest here (see Table 6).
-
(3)
In particular, if L is an odd prime, then
(17)where is a triangular number. We note that
by using
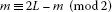 . If L is odd, then
. If L is odd, then -
(4)
In particular, if is an odd prime, then
(18)We introduce the twisted triangular numbers and given by
The first sixteen values of
are given in Table 7.
We can see from Figure 3 and Table 7 that when (resp. x) is prime, the numbers
(resp. ) and (resp. ) are the same.
-
(5)
A similar question regarding such convolution formulas has been addressed previously in [12]: Can one find , , , , m, , , β in ℤ satisfying
for a fixed u and for a fixed odd prime p?
We believe that such a problem is generally not easy to solve. Equations (17) and (18) are special cases for this question with and 1. A similar result is presented in [[12], (12)].
-
(6)
From Tables 6 and 7, we can easily obtain values of for any prime L.
-
(7)
In Table 8 we compare the properties of triangular numbers and twisted triangular numbers .
Remark 3.5 (An application)
Let us compute the quantity , that is,
where we refer to
in [[15], (3.10)] and
in [[15], Theorem 4]. Combining (19) and (12), we have Table 9.
From Theorem 1.3, for , we deduce that
Moreover, from (19) and (22), we see that
To refine the above formula, we use the following observation. Let p be a prime and . It is well known that
from [[2], p.26]. Now, if we set and use (23) and (24), we obtain
Remark 3.6 (Representations of N as the sum of m triangular numbers) We set . For and , we let
so that counts the number of representations of N as the sum of m triangular numbers. For , we have the classical result
see [[16], p.55].
From (26), (25), (20), Table 5, and [[17], p.401], we obtain Table 10.
From Theorem 2.2, we derive
and using Theorem 2.2 we get
with odd distinct primes.
3.6 Representation of an integer N as the sum of s squares
The s squares problem is to count the number of integer solutions of the Diophantine equation
where changing the sign of the order of the gives distinct solutions. Explicit formulas for were given by Legendre in 1798 and Gauss in 1801. In 1770 Lagrange gave formula for . Using the theory of theta functions, Jacobi obtained explicit formulas for , where . Glaisher used elliptic function methods rather than modular functions to obtain . A formula for was proved by Ramanujan. For more details, see [18] and references therein. In this subsection, we give a new formulation for in terms of and , and from our main result, we deduce a congruence formula for this number. Following Jacobi, we consider the equation
where is the case of the theta function in [19] given by
Jacobi [20] proved
From (29) and (23), we get a new formulation of in terms of and . In fact,
and then
which gives the following theorem. Here,
we refer to [[15], (3.10), (4.4)].
From the above computation, we have a beautiful arithmetical results, which we give now.
Theorem 3.7 Let . We have a formula
and if  is an odd integer, then
is an odd integer, then

Proof By using (30) and  , we get the theorem. □
, we get the theorem. □
Remark 3.8 Let M and N be odd integers with . From Theorem 3.7, we derive that
and
Corollary 3.9 Let be a prime decomposition of the integer N, and if  for all , then we have
for all , then we have

4 The problem
Sierpiński has asked if infinitely often. Jud McCranie found 832 solutions of
see[[21], p.103]).
We consider the values of and .
4.1 Further results
First, we shall compare the above problem for and .
The results of Table 11 were realized by combining several computers and by using Mathematica 8.0 software. It would be impossible for us to reproduce here all their details. It is clear, according to our numerical computations, that the study of the above problem with is faster than that of the one.
In fact, using Mathematica 8.0, we were able to obtain all positive integers for all in Table 11. Note that the results of in Table 11 are also presented in [[21], p.100, pp.103-104].
Theorem 4.1
-
(a)
If is an odd prime number, then .
-
(b)
If p and are odd prime numbers, then .
-
(c)
If is an odd prime number, then we get with and .
-
(d)
If n and are twin prime numbers, then .
-
(e)
If n is a positive integer, then we get Table 12.
Proof Let p be an odd positive integer. Using and , we get (a), (b), (d), and (e). In (c), if is an odd prime number with , then n is an odd number. It is easy to verify that
and . It is clear that . □
Corollary 4.2 Let p be an odd prime. If is an odd prime or , and is prime, then
Proof From Table 5, we get
From Theorem 4.1(a), (b), we know that and ; hence, the proof is completed. □
Lemma 4.3 Let with . Then , , is an injective map. In particular, there exists an injective sequence of ,
satisfying injective map.
Proof Let . By the definition of , we deduce that . From Theorem 2.2, we get and . And let and with , then and , . Therefore, is an injective map. It is clear that is an injective map. □
By Lemma 4.3, we deduce the corollary.
Corollary 4.4 Let m be a nonegative integer. If , then
4.2 Remarks and examples
We list the following interesting remarks and examples.
Remark 4.5
-
1.
(Sophie Germain primes) Note that if there are an infinite number of Sophie Germain primes, then the problem has an infinite number of solutions (in terms of prime numbers).
-
2.
(Mersenne numbers) Assume that . Then, by Theorem 2.2, we have . If the cardinal of the Mersenne primes or the cardinal of primes p, such that is also prime, is infinite, then by using Theorem 4.1(a), (b), the number of m satisfying and is infinite.
-
3.
(Perfect numbers) A positive integer n is called perfect if . Euclid and Euler showed that all even perfect numbers are of the form
In our case, we observe that . If there exists an odd positive integer m satisfying , then the number of n satisfying is infinite, that is, .
4.3 Numerical computations for the truncated sets
Let N be a positive integer and set . From Lemma 4.3 we see that the restricted map is still injective between and .
In this section, using Mathematica 8.0 we compute the sets for and . We obtain the following lists.
-
(a)
= { 6, 12, 14, 20, 33, 44, 62, 92, 116, 138, 164, 212, 254, 280, 308, 320, 332, 356, 452, 524, 572, 692, 716, 764, 932, 956, 1,004, 1,124, 1,172, 1,436, 1,496, 1,562, 1,676, 1,724, 1,772, 1,964, 2,002, 2,036, 2,132, 2,372, 2,564, 2,598, 2,612, 2,636, 2,732, 2,876, 2,913, 2,972, 3,044, 3,228, 3,236, 3,344, 3,408, 3,644, 3,812, 4,052, 4,076, 4,124, 4,187, 4,196, 4,292, 4,412, 4,728, 4,892, 4,916, 5,156, 5,170, 5,636, 5,756, 5,804, 5,924, 5,996, 6,044, 6,236, 6,332, 6,404, 6,764, 6,932, 7,169, 7,244, 7,424, 7,556, 7,604, 7,724, 7,892, 8,012, 8,050, 8,156, 8,234, 8,252, 8,276, 8,516, 8,564, 8,930, 9,092, 9,356, 9,359, 9,404, 9,572, 9,596, 9,836, 10,172, 10,196, 10,772, 10,796, 10,964, 11,012, 11,276, 11,612, 11,756, 11,852, 11,876, 12,092, 12,212, 12,565, 13,196, 13,316, 13,436, 13,556, 13,652, 13,796, 13,964, 14,156, 14,372, 14,492, 15,044, 15,085, 15,116, 15,212, 15,284, 15,404, 15,452, 15,644, 16,076, 16,120, 16,292, 16,376, 16,382, 16,844, 17,084, 17,396, 17,492, 17,564, 17,636, 17,924, 18,170, 18,932, 19,172, 19,484, 19,676, 19,772, 20,012, 20,156, 20,204, 20,324, 20,684, 20,924, 21,116, 21,212, 21,332, 21,461, 21,518, 21,596, 21,764, 22,004, 22,556, 22,844, 22,964, 23,396, 23,612, 24,212, 24,404, 24,452, 24,524, 24,692, 24,881, 25,019, 25,052, 25,076, 25,292, 25,316, 25,338, 25,796, 25,964, 26,084, 26,204, 26,252, 26,324, 26,609, 27,044, 27,596, 27,932, 28,172, 28,316, 28,412, 28,484, 28,604, 28,772, 28,844, 29,396, 29,696, 29,732, 30,164, 30,572, 30,596, 30,764, 31,292, 31,364, 31,532, 31,604, 32,276, 32,372, 32,444, 32,804, 32,972, 33,092, 33,590, 34,052, 34,652, 34,772, 34,964, 35,358, 35,804, 35,876, 36,116, 36,236, 36,884, 37,172, 37,484, 37,676, 37,892, 37,916, 38,156, 38,516, 38,756, 39,164, 40,244, 40,364, 40,458, 40,652, 41,012, 41,084, 41,252, 41,324, 42,116, 42,356, 42,452, 42,764, 42,836, 42,932, 43,124, 43,196, 43,532, 44,684, 45,078, 45,284, 45,476, 45,572, 45,884, 46,076, 46,196, 46,316, 46,796, 46,863, 47,132, 47,204, 47,252, 47,324, 47,636, 47,756, 47,792, 47,978, 48,044, 48,164, 48,404, 48,476, 48,812, 49,052, 49,225, 49,316, 50,612, 50,684, 51,164, 51,284, 51,596, 51,692, 51,835, 51,836, 52,004, 52,196, 52,916, 53,058, 53,252, 53,804, 53,852, 53,963, 54,212, 54,476, 54,596, 55,052, 55,532, 55,604, 55,652, 55,748, 56,036, 56,324, 56,612, 56,636, 56,996, 57,212, 57,284, 57,956, 58,056, 58,244, 58,484, 58,676, 58,796, 58,964, 59,132, 59,324, 59,516, 59,756, 59,987, 60,404, 60,644, 60,692, 60,932, 61,076, 61,604, 61,832, 62,276, 62,516, 63,092, 63,164, 63,212, 63,692, 64,004, 64,364, 65,012, 65,204, 65,684, 65,972, 66,212, 66,692, 67,244, 67,292, 67,532, 67,724, 68,636, 68,732, 69,164, 69,332, 69,404, 70,316, 70,676, 70,724, 71,756, 71,924, 72,164, 72,524, 72,596, 72,764, 72,836, 72,932, 73,364, 73,772, 73,844, 74,924, 75,092, 75,108, 75,212, 75,596, 76,652, 77,057, 77,204, 77,276, 77,492, 77,564, 77,732, 78,212, 78,236, 78,644, 78,836, 79,004, 79,292, 79,556, 79,652, 79,676, 79,964, 80,252, 80,996, 81,055, 81,476, 81,572, 81,644, 81,764, 82,772, 83,012, 83,036, 83,084, 83,156, 83,516, 83,684, 83,756, 83,852, 84,044, 84,356, 84,596, 84,716, 84,884, 85,364, 85,532, 85,676, 86,170, 86,444, 86,804, 86,852, 87,212, 87,572, 88,052, 88,316, 88,532, 89,036, 89,084, 89,372, 89,396, 89,636, 89,732, 89,876, 89,924, 90,164, 91,004, 91,412, 91,772, 92,396, 93,116, 93,284, 93,356, 93,836, 94,244, 94,412, 94,676, 95,012, 95,276, 95,636, 95,924, 96,812, 96,956, 97,124, 97,892, 98,036, 98,204, 98,444, 98,732, 98,996, 99,638, 99,884 }.
-
(b)
= { 12, 24, 28, 40, 51, 66, 88, 115, 124, 184, 232, 276, 319, 328, 424, 508, 560, 616, 640, 664, 712, 904, 1,003, 1,048, 1,144, 1,384, 1,432, 1,528, 1,864, 1,912, 2,008, 2,248, 2,344, 2,585, 2,872, 2,992, 3,124, 3,352, 3,448, 3,544, 3,928, 4,004, 4,072, 4,183, 4,195, 4,264, 4,744, 5,128, 5,196, 5,224, 5,272, 5,464, 5,752, 5,826, 5,944, 5,959, 6,088, 6,456, 6,472, 6,688, 6,816, 7,288, 7,624, 8,104, 8,152, 8,248, 8,374, 8,392, 8,584, 8,824, 9,456, 9,784, 9,832, 10,312, 10,340, 11,272, 11,512, 11,608, 11,659, 11,848, 11,992, 12,088, 12,367, 12,472, 12,561, 12,664, 12,808, 13,528, 13,581, 13,864, 14,338, 14,488, 14,848, 15,112, 15,208, 15,365, 15,448, 15,784, 16,024, 16,100, 16,312, 16,468, 16,504, 16,552, 17,032, 17,128, 17,860, 18,184, 18,712, 18,718, 18,808, 19,144, 19,192, 19,672, 20,344, 20,392, 20,541, 21,544, 21,592, 21,928, 22,024, 22,552, 23,224, 23,512, 23,704, 23,752, 24,184, 24,424, 25,130, 26,392, 26,632, 26,872, 27,112, 27,304, 27,592, 27,928, 28,312, 28,744, 28,984, 29,393, 30,088, 30,170, 30,232, 30,424, 30,568, 30,808, 30,904, 31,288, 32,152, 32,240, 32,584, 32,665, 32,752, 32,764, 33,688, 34,168, 34,792, 34,984, 35,128, 35,272, 35,848, 36,340, 37,864, 38,344, 38,968, 39,352, 39,544, 39,913, 40,024, 40,312, 40,408, 40,648, 41,368, 41,848, 42,232, 42,423, 42,424, 42,664, 42,922, 43,036, 43,192, 43,528, 44,008, 45,112, 45,688, 45,928, 46,792, 47,224, 47,841, 48,424, 48,808, 48,904, 49,048, 49,384, 49,762, 50,038, 50,104, 50,152, 50,435, 50,584, 50,632, 50,676, 51,592, 51,928, 52,168, 52,408, 52,504, 52,648, 53,218, 54,088, 55,192, 55,864, 56,344, 56,632, 56,824, 56,968, 57,208, 57,544, 57,688, 58,792, 59,392, 59,464, 60,328, 61,144, 61,192, 61,528, 62,584, 62,728, 63,064, 63,208, 64,552, 64,744, 64,888, 65,608, 65,944, 66,184, 67,180, 68,104, 69,304, 69,544, 69,928, 70,716, 71,608, 71,752, 72,232, 72,472, 73,768, 74,344, 74,968, 75,352, 75,784, 75,832, 76,312, 77,032, 77,512, 78,328, 80,488, 80,728, 80,916, 81,304, 82,024, 82,168, 82,504, 82,648, 84,232, 84,712, 84,904, 85,528, 85,672, 85,864, 86,248, 86,392, 87,064, 88,303, 89,368, 90,156, 90,568, 90,952, 91,144, 91,768, 92,152, 92,392, 92,599, 92,632, 93,592, 93,726, 94,264, 94,408, 94,504, 94,648, 95,272, 95,512, 95,584, 95,956, 96,088, 96,328, 96,808, 96,952, 97,624, 98,104, 98,450, 98,632}.
-
(c)
= { 15, 24, 48, 56, 69, 80, 87, 102, 132, 175, 176, 230, 248, 368, 464, 552, 638, 656, 689, 848, 1,016, 1,120, 1,127, 1,232, 1,280, 1,328, 1,349, 1,424, 1,808, 2,006, 2,096, 2,288, 2,768, 2,864, 3,056, 3,728, 3,824, 4,016, 4,496, 4,688, 5,170, 5,744, 5,984, 6,248, 6,704, 6,896, 7,088, 7,856, 8,008, 8,144, 8,366, 8,390, 8,528, 9,488, 10,256, 10,392, 10,448, 10,544, 10,928, 11,504, 11,652, 11,888, 11,918, 12,176, 12,912, 12,944, 13,376, 13,632, 14,576, 15,248, 16,208, 16,304, 16,496, 16,748, 16,784, 17,168, 17,648, 18,912, 19,511, 19,568, 19,664, 19,829, 20,624, 20,680, 22,544, 23,024, 23,216, 23,318, 23,696, 23,984, 24,176, 24,597, 24,734, 24,944, 25,122, 25,328, 25,616, 27,056, 27,162, 27,728, 28,676, 28,976, 29,696, 30,224, 30,416, 30,730, 30,896, 31,568, 32,048, 32,200, 32,624, 32,936, 33,008, 33,104, 34,064, 34,256, 35,720, 36,368, 37,391, 37,424, 37,436, 37,616, 37,901, 38,288, 38,384, 39,344, 40,688, 40,784, 41,082, 43,088, 43,184, 43,856, 44,048, 45,104, 45,925, 46,448, 47,024, 47,408, 47,487, 47,504, 48,368, 48,848, 50,260, 52,784, 53,264, 53,744, 54,224, 54,608, 55,184, 55,856, 56,624, 57,488, 57,968, 58,786, 59,125, 60,176, 60,340, 60,464, 60,848, 61,053, 61,136, 61,616, 61,808, 62,576, 64,304, 64,480, 65,168, 65,330, 65,504, 65,528, 67,376, 68,336, 69,584, 69,968, 70,256, 70,544, 71,696, 72,680, 75,728, 76,688, 77,936, 78,704, 79,088, 79,826, 80,048, 80,624, 80,816, 81,296, 81,989, 82,736, 83,696, 84,464, 84,846, 84,848, 85,328, 85,844, 86,072, 86,384, 87,056, 88,016, 90,224, 91,376, 91,856, 93,584, 94,448, 95,682, 96,848, 97,557, 97,616, 97,808, 98,096, 98,768, 99,524, 99,827}.
-
(d)
= { 30, 48, 55, 96, 112, 138, 160, 174, 204, 205, 264, 350, 352, 355, 460, 496, 736, 928, 1,104, 1,276, 1,293, 1,312, 1,378, 1,696, 2,032, 2,240, 2,254, 2,464, 2,560, 2,656, 2,698, 2,848, 3,277, 3,616, 3,669, 4,012, 4,192, 4,576, 5,536, 5,728, 6,112, 7,456, 7,648, 8,032, 8,992, 9,376, 9,853, 10,340, 11,488, 11,968, 12,496, 12,549, 13,408, 13,792, 13,899, 14,176, 14,857, 15,712, 16,016, 16,288, 16,732, 16,780, 17,056, 18,976, 20,512, 20,784, 20,896, 21,088, 21,856, 23,008, 23,287, 23,304, 23,776, 23,836, 24,352, 25,824, 25,888, 26,077, 26,752, 27,264, 29,152, 30,496, 32,416, 32,608, 32,992, 33,496, 33,568, 34,336, 35,296, 36,669, 37,824, 39,022, 39,136, 39,187, 39,328, 39,658, 41,248, 41,360, 41,525, 45,088, 46,048, 46,432, 46,636, 47,392, 47,968, 48,352, 49,194, 49,468, 49,888, 50,244, 50,656, 51,232, 54,112, 54,324, 55,456, 56,743, 57,352, 57,952, 59,392, 60,448, 60,832, 61,460, 61,792, 63,136, 64,096, 64,400, 64,963, 65,248, 65,872, 66,016, 66,208, 68,128, 68,512, 71,440, 72,736, 73,321, 74,782, 74,848, 74,872, 75,232, 75,802, 76,576, 76,768, 78,688, 81,376, 81,568, 82,164, 85,839, 86,176, 86,368, 87,712, 88,096, 90,208, 90,637, 91,850, 92,896, 94,048, 94,816, 94,974, 95,008, 95,113, 96,193, 96,736, 97,696}.
-
(e)
= { 60, 96, 110, 177, 192, 224, 276, 303, 320, 348, 408, 410, 528, 605, 700, 704, 710, 749, 920, 992, 1,045, 1,157, 1,472, 1,856, 2,208, 2,552, 2,567, 2,586, 2,624, 2,756, 3,392, 4,064, 4,480, 4,508, 4,533, 4,928, 5,120, 5,312, 5,396, 5,696, 6,554, 7,232, 7,338, 7,697, 8,024, 8,384, 9,152, 10,547, 11,072, 11,456, 12,224, 13,199, 14,912, 15,296, 16,064, 16,345, 17,984, 18,752, 19,706, 20,381, 20,680, 21,197, 21,797, 22,976, 23,936, 24,992, 25,075, 25,098, 26,816, 27,584, 27,798, 28,352, 29,321, 29,365, 29,714, 31,424, 32,032, 32,576, 32,849, 33,464, 33,560, 34,112, 37,929, 37,952, 41,024, 41,568, 41,792, 42,176, 43,712, 46,016, 46,574, 46,608, 47,552, 47,672, 48,704, 51,648, 51,776, 52,154, 53,504, 54,528, 58,304, 60,992, 61,705, 64,832, 65,216, 65,984, 66,992, 67,136, 68,672, 70,049, 70,592, 73,338, 75,648, 78,044, 78,272, 78,374, 78,656, 79,316, 82,496, 82,720, 83,050, 85,769, 89,033, 90,176, 92,096, 92,864, 93,272, 94,784, 95,936, 96,704, 98,388, 98,936, 99,776}.
We conclude this paper by the following remark.
Remark 4.6 According to the obtained numerical results, it is interesting to study lower and upper bounds for the cardinality of the sets . In the same manner we can also study the asymptotic behavior of this cardinality. This would allow us to know whether or not the full is infinite.
References
Berndt BC: Ramanujan’s Notebook, Part II. Springer, Berlin; 1989.
Williams KS London Mathematical Society Student Texts 76. In Number Theory in the Spirit of Liouville. Cambridge University Press, Cambridge; 2011.
Royer E: Evaluating convolution sums of the divisor function by quasimodular forms. Int. J. Number Theory 2007, 3(2):231–261. 10.1142/S1793042107000924
Ramakrishnan, B, Sahu, B: Evaluation of the convolution sums and and an application. Int. J. Number Theory (2012, accepted)
Alaca S, Williams KS:Evaluation of the convolution sums and . J. Number Theory 2007, 124(2):491–510. 10.1016/j.jnt.2006.10.004
Alaca A, Alaca S, Uygul F, Williams KS: Restricted Eisenstein series and certain convolution sums. J. Comb. Number Theory 2011, 3: 1–14.
Adiga C, Ramaswamy HN: A note on certain divisibility problem. Int. J. Math. Anal. 2008, 2(24):1157–1161.
Simsek Y: Elliptic analogue of the Hardy sums related to elliptic Bernoulli functions. Gen. Math. 2007, 15(2–3):3–23.
Gyory K, Dujella A, Pinter A: On the power values of pyramidal numbers, I. Acta Arith. 2012, 155: 217–226. 10.4064/aa155-2-9
Silverman JH: The Arithmetic of Elliptic Curves. Springer, Berlin; 1986.
Dickson LE II. In History of the Theory of Numbers. Chelsea, New York; 1952.
Kim A, Kim D, Li Y: Convolution sums arising from the divisor functions. J. Korean Math. Soc. 2013, 50(2):331–360. 10.4134/JKMS.2013.50.2.331
Garge AS, Shirali SA: Triangular numbers. Resonance 2012, 17(7):672–681. 10.1007/s12045-012-0074-z
Hoggatt VE Jr., Bicknell M: Triangular numbers. Fibonacci Q. 1974, 12: 221–230.
Huard JG, Ou ZM, Spearman BK, Williams KS: Elementary evaluation of certain convolution sums involving divisor functions. II. Number Theory for the Millennium 2002, 229–274.
Cheng N, Williams KS: Evaluation of some convolution sums involving the sum of divisors functions. Yokohama Math. J. 2005, 52: 39–57.
Andrew GE, Berndt BC: Ramanujan’s Lost Notebook, Part I. Springer, Berlin; 2005.
Milne S: New infinite families of exact sums of squares formulas, Jacobi elliptic functions, and Ramanujan’s tau function. Proc. Natl. Acad. Sci. USA 1996, 93: 15004–15008. 10.1073/pnas.93.26.15004
Whittaker ET, Watson GN: A Course of Modern Analysis. 4th edition. Cambridge University Press, Cambridge; 1927:464–498.
Jacobi, CGJ: Fundamenta Nova Theoriae Functionum Ellipticarum, Sumptibus Fratrum Bornträger. Reprinted in C.G.J. Jacobi, Gesammelte Werke, vol. 1, pp. 49–239. Reimer, Berlin (1881–1891)
Guy RK: Unsolved Problems in Number Theory. Springer, Berlin; 2004.
Acknowledgements
Dedicated to Professor Hari M Srivastava.
This research was supported by the National Institute for Mathematical Sciences (NIMS) grant funded by the Korea government (B21303) and the ‘Equipe Ananlyse et Probabilités’ of the Department of Mathematics at University of Evry.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, D., Bayad, A. Convolution identities for twisted Eisenstein series and twisted divisor functions. Fixed Point Theory Appl 2013, 81 (2013). https://doi.org/10.1186/1687-1812-2013-81
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2013-81
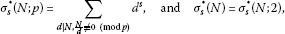
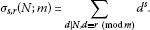


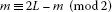 . If L is odd, then
. If L is odd, then 