Coincidence point theorems in quasi-metric spaces without assuming the mixed monotone property and consequences in G-metric spaces

Abstract

In this paper, we present some coincidence point theorems in the setting of quasi-metric spaces that can be applied to operators which not necessarily have the mixed monotone property. As a consequence, we particularize our results to the field of metric spaces, partially ordered metric spaces and G-metric spaces, obtaining some very recent results. Finally, we show how to use our main theorems to obtain coupled, tripled, quadrupled and multidimensional coincidence point results.

1 Introduction

In recent times, one of the branches of fixed point theory that has attracted much attention is the field devoted to studying this kind of results in the setting of partially ordered metric spaces. After the appearance of the first works in this sense (by Ran and Reurings [1], by Nieto and Rodríguez-López [2], by Gnana-Bhaskar and Lakshmikantham [3], and by Lakshmikantham and Ćirić [4], to cite some of them), the literature on this topic has expanded significantly. In [3], the authors introduced the notion of mixed monotone property, which has been one of the most usual hypotheses in this kind of results. However, some theorems avoiding these conditions have appeared very recently (see, for instance, [5]). One of the results on this line of study was given by Charoensawan and Thangthong in [6]. To understand their statement, the following notions were considered.

Definition 1.1 Let $(X,d)$ be a metric space and $F:X\times X\to X$ and $g:X\to X$ be given mappings. Let M be a nonempty subset of $X^6$. We say that M is an $(F^{\ast },g)$ -invariant subset of $X^6$ if and only if for all $x,y,z,u,v,w\in X$,

• 1. $(x,u,y,v,z,w)\in M\iff (w,z,v,y,u,x)\in M$;

• 2. $(gx,gu,gy,gv,gz,gw)\in M\Rightarrow (F(x,u),F(u,x),F(y,v),F(v,y),F(z,w),F(w,z))\in M$.

Definition 1.2 Let $(X,d)$ be a metric space and M be a subset of $X^6$. We say that M satisfies the transitive property if and only if for all $x,y,w,z,a,b,c,d,e,f\in X$,

$$(x,y,w,z,a,b)\in M\text{and}(a,b,c,d,e,f)\in M\Rightarrow (x,y,w,z,e,f)\in M.$$

Definition 1.3 Let Φ be the family of all functions $\phi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ satisfying

• 1. ${\phi }^{-1}(\{0\})=\{0\}$,

• 2. $\phi (t)<t$ for all $t>0$,

• 3. ${lim}_{s\to t^{+}}\phi (s)<t$ for all $t>0$.

Using the previous preliminaries, they proved the following result in the context of G-metric spaces, which is recalled in Section 2.1.

Theorem 1.1 (Charoensawan and Thangthong [6], Theorem 3.1)

Let $(X,\preccurlyeq )$ be a partially ordered set and G be a G-metric on X such that $(X,G)$ is a complete G-metric space, and let M be a nonempty subset of $X^6$. Assume that there exists $\phi \in \mathrm{\Phi }$ and also suppose that $F:X\times X\to X$ and $g:X\to X$ such that

$$\begin{array}{r}[G(F(x,u),F(y,v),F(z,w))+G(F(u,x),F(v,y),F(w,z))]\\ \le \varphi (G(gx,gy,gz)+G(gu,gv,gw))\end{array}$$

(1)

for all $(gx,gu,gy,gv,gz,gw)\in M$.

Suppose also that F is continuous, $F(X\times X)\subseteq g(X)$ and g is continuous and commutes with F. If there exist $x_0,y_0\in X$ such that

$$(F(x_0,y_0),F(y_0,x_0),F(x_0,y_0),F(y_0,x_0),g{x}_0,g{y}_0)\in M$$

and M is an $(F^{\ast },g)$-invariant set which satisfies the transitive property, then there exist $x,y\in X$ such that $gx=F(x,y)$ and $gy=F(y,x)$.

First of all, notice that the partial order ≼ in the hypothesis has no sense in the statement of Theorem 1.1. This is only a mistake that proves the special importance of partial orders in this class of results.

In this paper, we show that Theorem 1.1 can be easily deduced from a unidimensional version of the same result. In fact, we prove that the middle variables of $M\subseteq X^6$ are unnecessary. But the main aim of this work is to obtain some coincidence point theorems in the context of quasi-metric spaces that can be applied in several frameworks, including metric spaces and G-metric spaces. The hypotheses of our main results are very general, and they can be particularized in a variety of different contexts, unidimensional or multidimensional ones, even if the involved mappings do not have the mixed monotone property. Our results also extend and unify some recent theorems that can be found in [7]. As a consequence, we prove that many results in this field of study can be easily derived from our statements.

2 Preliminaries

For the sake of completeness, we collect in this section some basic definitions and well-known results in this field. Firstly, let ℕ and ℝ denote the sets of all positive integers and all real numbers, respectively. Furthermore, we let ${\mathbb{N}}_0=\mathbb{N}\cup \{0\}$. If $A\subseteq \mathbb{R}$ is a nonempty subset of ℝ, the Euclidean metric on A is $d(x,y)=|x-y|$ for all $x,y\in A$. In the sequel, let X be a nonempty set. Given a natural number n, we use $X^n$ to denote the nth Cartesian power of X, that is, $X\times X\times \cdots \times X$ (n times).

From now on, let $T:X\to X$ be a self-mapping (also called operator). For simplicity, we denote $T(x)$ by Tx and $T\circ T$ by $T^2$. In general, the iterates of a self-mapping T are the mappings ${\{T^n:X\to X\}}_{n\ge 0}$ defined by

$$\begin{array}{r}{T}^0=\text{identity mapping on }X,T^1=T,T^2=T\circ T,\\ T^{n+1}=T\circ T^n\text{for all }n\ge 2.\end{array}$$

Given a point $x\in X$, the Picard sequence of the operator T (based on x) is the sequence ${\{T^{n}x\}}_{n\ge 0}$, which we will denote by $\{x_n\}$.

The main aim of this manuscript is to show some sufficient conditions to ensure existence and uniqueness of the following kinds of points. A coincidence point of two mappings $T,g:X\to X$ is a point $x\in X$ such that $Tx=gx$. And a coupled coincidence point of two mappings $F:X^2\to X$ and $g:X\to X$ is a point $(x,y)\in X^2$ such that $F(x,y)=gx$ and $F(y,x)=gy$. If g is the identity mapping on X, then both kinds of points are called coupled fixed point of T and coupled fixed point of F, respectively.

A metric (or a distance function) on a nonempty set X is a mapping $d:X\times X\to [0,\mathrm{\infty })$ verifying the following conditions: for all $x,y,z\in X$,

$$\begin{array}{ll}({\mathrm{M}}_1)d(x,x)=0;& ({\mathrm{M}}_2)d(x,y)>0\text{if }x\ne y;\\ ({\mathrm{M}}_3)d(x,y)=d(y,x);& ({\mathrm{M}}_4)d(x,y)\le d(x,z)+d(z,y).\end{array}$$

In such a case, the pair $(X,d)$ is called a metric space.

We say that two mappings $T,g:X\to X$ are commuting if $gTx=Tgx$ for all $x\in X$. We say that $F:X^n\to X$ and $g:X\to X$ are commuting if $gF(x_1,x_2,\dots ,x_n)=F(g{x}_1,g{x}_2,\dots ,g{x}_n)$ for all $x_1,\dots ,x_n\in X$.

A binary relation on X is a nonempty subset ℛ of $X^2$. For simplicity, we will write $x\preccurlyeq y$ if $(x,y)\in \mathcal{R}$, and we will say that ≼ is the binary relation. We will write $x\prec y$ when $x\preccurlyeq y$ and $x\ne y$, and we will write $y\succcurlyeq x$ when $x\preccurlyeq y$. We will say that x and y are ≼-comparable if $x\preccurlyeq y$ or $y\preccurlyeq x$.

A binary relation ≼ on X is transitive if $x\preccurlyeq z$ for all $x,y,z\in X$ such that $x\preccurlyeq y$ and $y\preccurlyeq z$. A preorder (or a quasi-order) ≼ on X is a binary relation on X that is reflexive (i.e., $x\preccurlyeq x$ for all $x\in X$) and transitive. In such a case, we say that $(X,\preccurlyeq )$ is a preordered space (or a preordered set). If a preorder ≼ is also antisymmetric ($x\preccurlyeq y$ and $y\preccurlyeq x$ implies $x=y$), then ≼ is called a partial order, and $(X,\preccurlyeq )$ is a partially ordered space.

If $(X,\preccurlyeq )$ is a preordered space and $T,g:X\to X$ are two mappings, we say that T is a $(g,\preccurlyeq )$ -nondecreasing mapping if $Tx\preccurlyeq Ty$ for all $x,y\in X$ such that $gx\preccurlyeq gy$. If g is the identity mapping on X, T is nondecreasing w.r.t. ≼ (or it is ≼-nondecreasing).

If $(X,d)$ is a metric space, a mapping $T:X\to X$ is continuous if $\{T{x}_n\}\to Tz$ for all sequences $\{x_n\}\subseteq X$ such that $\{x_n\}\to z\in X$. If ≼ is a binary relation on X, we say that T is $(g,\preccurlyeq )$ -nondecreasing-continuous if $\{T{x}_n\}\to Tz$ for all sequences $\{x_n\}\subseteq X$ such that $\{x_n\}\to z\in X$ verifying that $g{x}_n\preccurlyeq g{x}_{n+1}$ for all $n\in \mathbb{N}$. If g is the identity mapping on X, we say that T is ≼-nondecreasing-continuous.

2.1 G-metric spaces

The notion of G-metric space is defined as follows.

Definition 2.1 (Mustafa and Sims [8])

Let X be a nonempty set, and let $G:X\times X\times X\to {\mathbb{R}}^{+}$ be a function satisfying the following properties:

(G₁) $G(x,y,z)=0$ if $x=y=z$;

(G₂) $0<G(x,x,y)$ for all $x,y\in X$ with $x\ne y$;

(G₃) $G(x,x,y)\le G(x,y,z)$ for all $x,y,z\in X$ with $y\ne z$;

(G₄) $G(x,y,z)=G(x,z,y)=G(y,z,x)=\cdots$ (symmetry in all three variables);

(G₅) $G(x,y,z)\le G(x,a,a)+G(a,y,z)$ (rectangle inequality) for all $x,y,z,a\in X$.

Then the function G is called a generalized metric, or, more specifically, a G-metric on X, and the pair $(X,G)$ is called a G-metric space.

Note that every G-metric on X induces a metric $d_G$ on X defined by

$$d_G(x,y)=G(x,y,y)+G(y,x,x)\text{for all }x,y\in X.$$

For a better understanding of the subject, we give the following examples of G-metrics.

Example 2.1 Let $(X,d)$ be a metric space. The function $G:X\times X\times X\to [0,+\mathrm{\infty })$, defined by

$$G(x,y,z)=max\{d(x,y),d(y,z),d(z,x)\}$$

for all $x,y,z\in X$, is a G-metric on X.

Example 2.2 (see, e.g., [8])

Let $X=[0,\mathrm{\infty })$. The function $G:X\times X\times X\to [0,\mathrm{\infty })$, defined by

$$G(x,y,z)=|x-y|+|y-z|+|z-x|$$

for all $x,y,z\in X$, is a G-metric on X.

In their initial paper, Mustafa and Sims [8] also defined the basic topological concepts in G-metric spaces as follows.

Definition 2.2 (Mustafa and Sims [8])

Let $(X,G)$ be a G-metric space, and let $\{x_n\}$ be a sequence of points of X. We say that $\{x_n\}$ is G-convergent to $x\in X$ if

$$\underset{n,m\to \mathrm{\infty }}{lim}G(x,x_n,x_m)=0,$$

that is, for any $\epsilon >0$, there exists $N\in \mathbb{N}$ such that $G(x,x_n,x_m)<\epsilon$ for all $n,m\ge N$. We call x the limit of the sequence, and we write $\{x_n\}\to x$ or ${lim}_{n\to \mathrm{\infty }}{x}_n=x$.

It is clear that the limit of a convergent sequence is unique.

Proposition 2.1 (Mustafa and Sims [8])

In a G-metric space $(X,G)$, the following conditions are equivalent.

• 1. $\{x_n\}$ is G-convergent to x.

• 2. $G(x_n,x_n,x)\to 0$ as $n\to \mathrm{\infty }$.

• 3. $G(x_n,x,x)\to 0$ as $n\to \mathrm{\infty }$.

Definition 2.3 (Mustafa and Sims [8])

Let $(X,G)$ be a G-metric space. A sequence $\{x_n\}$ is called a G-Cauchy sequence if, for any $\epsilon >0$, there exists $N\in \mathbb{N}$ such that $G(x_n,x_m,x_l)<\epsilon$ for all $m,n,l\ge N$, that is, $G(x_n,x_m,x_l)\to 0$ as $n,m,l\to \mathrm{\infty }$.

Proposition 2.2 (Mustafa and Sims [8])

In a G-metric space $(X,G)$, the following conditions are equivalent.

• 1. The sequence $\{x_n\}$ is G-Cauchy.

• 2. For any $\epsilon >0$, there exists $N\in \mathbb{N}$ such that $G(x_n,x_m,x_m)<\epsilon$ for all $m,n\ge N$.

Definition 2.4 (Mustafa and Sims [8])

A G-metric space $(X,G)$ is called G-complete if every G-Cauchy sequence is G-convergent in $(X,G)$.

Definition 2.5 Let $(X,G)$ be a G-metric space. A mapping $T:X\to X$ is said to be G-continuous if $\{T{x}_n\}$ G-converges to Tx for any G-convergent sequence $\{x_n\}$ to $x\in X$. In general, given $m\in \mathbb{N}$, a mapping $F:X^m\to X$ is said to be G-continuous if $\{F(x_n^1,x_n^2,\dots ,x_n^m)\}$ G-converges to $F(x^1,x^2,\dots ,x^m)$ for any G-convergent sequences $\{x_n^1\},\{x_n^2\},\dots ,\{x_n^m\}\subseteq X$ such that $\{x_n^i\}\to x^i\in X$ for all $i\in \{1,2,\dots ,m\}$.

The following lemma shows a simple way to consider some G-metrics on $X^2$ from a G-metric on X.

Lemma 2.1 (Agarwal et al. [9])

Let $G:X^3\to [0,\mathrm{\infty })$ and $G_s^2,G_m^2:{(X^2)}^3\to [0,\mathrm{\infty })$ be three mappings verifying

$$\begin{array}{r}{G}_s^2((x_1,y_1),(x_2,y_2),(x_3,y_3))=G(x_1,x_2,x_3)+G(y_1,y_2,y_3)\mathit{\text{and}}\\ G_m^2((x_1,y_1),(x_2,y_2),(x_3,y_3))=max\{G(x_1,x_2,x_3),G(y_1,y_2,y_3)\}\\ \mathit{\text{for all }}{x}_1,x_2,x_3,y_1,y_2,y_3\in X.\end{array}$$

Then the following conditions are equivalent.

• (a) G is a $G^{\ast }$-metric on X.

• (b) $G_s^2$ is a $G^{\ast }$-metric on $X^2$.

• (c) $G_m^2$ is a $G^{\ast }$-metric on $X^2$.

In such a case, the following properties hold.

• 1. Every sequence $\{(x_n,y_n)\}\subseteq X^2$ verifies: $\{(x_n,y_n)\}\stackrel{G_s^2}{⟶}(x,y)⟺\{(x_n,y_n)\}\stackrel{G_m^2}{⟶}(x,y)⟺[\{x_n\}\stackrel{G}{⟶}x\mathit{\text{ and }}\{y_n\}\stackrel{G}{⟶}y]$.

• 2. $\{(x_n,y_n)\}\subseteq X^2$ is $G_s^2$-Cauchy ⟺ $\{(x_n,y_n)\}$ is $G_m^2$-Cauchy ⟺ $[\{x_n\}\mathit{\text{ and }}\{y_n\}\mathit{\text{ are }}G\mathit{\text{-Cauchy}}]$.

• 3. $(X,G)$ is G-complete ⟺ $(X^2,G_s^2)$ is G-complete ⟺ $(X^2,G_m^2)$ is G-complete.

2.2 Quasi-metric spaces

Definition 2.6 A mapping $q:X\times X\to [0,\mathrm{\infty })$ is a quasi-metric on X if it satisfies (M₁), (M₂) and (M₄), that is, if it verifies, for all $x,y,z\in X$:

(q₁) $q(x,y)=0$ if and only if $x=y$,

(q₂) $q(x,y)\le q(x,z)+q(z,y)$.

In such a case, the pair $(X,q)$ is called a quasi-metric space.

Remark 2.1 Any metric space is a quasi-metric space, but the converse is not true in general.

Now, we recollect some basic topological notions and related results about quasi-metric spaces (see also, e.g., [10–13]).

Definition 2.7 Let $(X,q)$ be a quasi-metric space, $\{x_n\}$ be a sequence in X, and $x\in X$. We will say that:

• $\{x_n\}$ converges to x (and we will denote it by $\{x_n\}\stackrel{q}{⟶}x$ or by $\{x_n\}\to x$) if ${lim}_{n\to \mathrm{\infty }}q(x_n,x)={lim}_{n\to \mathrm{\infty }}q(x,x_n)=0$;

• $\{x_n\}$ is a Cauchy sequence if for all $\epsilon >0$, there exists $n_0\in \mathbb{N}$ such that $q(x_n,x_m)<\epsilon$ for all $n,m\ge n_0$.

The quasi-metric space $(X,q)$ is said to be complete if every Cauchy sequence is convergent on $(X,q)$.

As q is not necessarily symmetric, some authors distinguished between left/right Cauchy/convergent sequences and completeness.

Definition 2.8 (Jleli and Samet [14])

Let $(X,q)$ be a quasi-metric space, $\{x_n\}$ be a sequence in X, and $x\in X$. We say that:

• $\{x_n\}$ right-converges to x if ${lim}_{n\to \mathrm{\infty }}q(x_n,x)=0$;

• $\{x_n\}$ left-converges to x if ${lim}_{n\to \mathrm{\infty }}q(x,x_n)=0$;

• $\{x_n\}$ is a right-Cauchy sequence if for all $\epsilon >0$ there exists $n_0\in \mathbb{N}$ such that $q(x_n,x_m)<\epsilon$ for all $m>n\ge n_0$;

• $\{x_n\}$ is a left-Cauchy sequence if for all $\epsilon >0$ there exists $n_0\in \mathbb{N}$ such that $q(x_m,x_n)<\epsilon$ for all $m>n\ge n_0$;

• $(X,q)$ is right-complete if every right-Cauchy sequence is right-convergent;

• $(X,q)$ is left-complete if every left-Cauchy sequence is left-convergent;

Remark 2.2 (see, e.g., [14])

A sequence $\{x_n\}$ in a quasi-metric space is Cauchy if and only if it is left-Cauchy and right-Cauchy.

Remark 2.3

• 1. The limit of a sequence in a quasi-metric space, if it exists, is unique. However, this is false if we consider right-limits or left-limits.

• 2. If $\{x_n\}\to x$ and $\{y_n\}\to y$ in a quasi-metric space, then $\{q(x_n,y_n)\}\to q(x,y)$, that is, q is continuous in both arguments. It follows from

  $$q(x,y)-q(x,x_n)-q(y_n,y)\le q(x_n,y_n)\le q(x_n,x)+q(x,y)+q(y,y_n)$$

for all n. In particular, $\{q(x_n,z)\}\to q(x,z)$ and $\{q(z,x_n)\}\to q(z,x)$ for all $z\in X$.

• 3. If $\{x_n\}\to x$, $\{q(x_n,y_n)\}\to 0$ and $\{q(y_n,x_n)\}\to 0$, then $\{y_n\}\to x$. It follows from

  $$q(y_n,x)\le q(y_n,x_n)+q(x_n,x)\text{and}q(x,y_n)\le q(x,x_n)+q(x_n,y_n).$$

• 4. If a sequence $\{x_n\}$ has a right-limit x and a left-limit y, then $x=y$, $\{x_n\}$ converges and it has an only limit (from the right and from the left). However, it is possible that a sequence has two different right-limits when it has no left-limit.

Example 2.3 Let X be a subset of ℝ containing $[0,1]$ and define, for all $x,y\in X$,

$$q(x,y)=\{\begin{array}{ll}x-y,& \text{if }x\ge y,\\ 1,& \text{otherwise}.\end{array}$$

Then $(X,q)$ is a quasi-metric space. Notice that $\{q(1/n,0)\}\to 0$ but $\{q(0,1/n)\}\to 1$. Therefore, $\{1/n\}$ right-converges to 0 but it does not converge from the left.

The following result shows a simple way to consider quasi-metrics from G-metrics.

Lemma 2.2 (Agarwal et al. [9])

Let $(X,G)$ be a G-metric space, and let us define $q_G,q_G^{\prime }:X^2\to [0,\mathrm{\infty })$ by

$$q_G(x,y)=G(x,y,y)\mathit{\text{and}}{q}_G^{\prime }(x,y)=G(x,x,y)\mathit{\text{for all }}x,y\in X.$$

Then the following properties hold.

• 1. $q_G$ and $q_G^{\prime }$ are quasi-metrics on X. Moreover,

  $$q_G^{\prime }(x,y)\le 2q_G(x,y)\le 4q_G^{\prime }(x,y)\mathit{\text{for all }}x,y\in X.$$

  (2)

• 2. In $(X,q_G)$ and in $(X,q_G^{\prime })$, a sequence is right-convergent (respectively, left-convergent) if and only if it is convergent. In such a case, its right-limit, its left-limit and its limit coincide.

• 3. In $(X,q_G)$ and in $(X,q_G^{\prime })$, a sequence is right-Cauchy (respectively, left-Cauchy) if and only if it is Cauchy.

• 4. In $(X,q_G)$ and in $(X,q_G^{\prime })$, every right-convergent (respectively, left-convergent) sequence has a unique right-limit (respectively, left-limit).

• 5. If $\{x_n\}\subseteq X$ and $x\in X$, then $\{x_n\}\stackrel{G}{⟶}x⟺\{x_n\}\stackrel{q_G}{⟶}x⟺\{x_n\}\stackrel{q_G^{\prime }}{⟶}x$.

• 6. If $\{x_n\}\subseteq X$, then $\{x_n\}$ is G-Cauchy ⟺ $\{x_n\}$ is $q_G$-Cauchy ⟺ $\{x_n\}$ is $q_G^{\prime }$-Cauchy.

• 7. $(X,G)$ is complete ⟺ $(X,q_G)$ is complete ⟺ $(X,q_G^{\prime })$ is complete.

2.3 Control functions

Functions in Φ (see Definition 1.3) verify the following properties.

Lemma 2.3 Let $\phi \in \mathrm{\Phi }$.

• 1. $\phi (t)\le t$ for all $t\ge 0$.

• 2. If $\{t_n\}\subset [0,\mathrm{\infty })$ is a sequence such that $t_{n+1}\le \phi (t_n)$ for all n, then $\{t_n\}\to 0$.

• 3. If $\{t_n\},\{s_n\}\subset [0,\mathrm{\infty })$ are two sequences such that $\{t_n\}\to 0$ and $s_n\le \phi (t_n)$ for all n, then $\{s_n\}\to 0$.

Proof (2) By item 1, $t_{n+1}\le \phi (t_n)\le t_n$ for all n, so $\{t_n\}$ is a nonincreasing sequence of nonnegative real numbers. Then it is convergent. Let $L={lim}_{n\to \mathrm{\infty }}{t}_n\ge 0$. We claim that $L=0$. If $L>0$, then $\{t_n\}$ is a sequence of numbers greater than L that converges to L. Hence,

$$L=\underset{n\to \mathrm{\infty }}{lim}{t}_{n+1}\le \underset{n\to \mathrm{\infty }}{lim}\phi (t_n)=\underset{s\to L^{+}}{lim}\phi (s)<L,$$

which is a contradiction.

• (3) It follows from item 2 taking into account that $0\le s_n\le \phi (t_n)\le t_n$ for all n. □

Inspired by Boyd and Wong’s theorem [15], Mukherjea [16] introduced the following kind of control functions:

$$\mathrm{\Psi }=\{\phi :[0,\mathrm{\infty })\to [0,\mathrm{\infty }):\phi (t)<t\text{ and }\underset{r\to t^{+}}{lim}\phi (r)<t\text{ for each }t>0\}.$$

Functions in Ψ are more general than those in Φ. The following properties are very useful.

Lemma 2.4 Let $\phi \in \mathrm{\Psi }$ be a mapping, and let $\{t_m\}\subset [0,\mathrm{\infty })$ be a sequence.

• 1. If $t_{m+1}\le \phi (t_m)$ and $t_m\ne 0$ for all m, then $\{t_m\}\to 0$.

• 2. Let $\{t_n\},\{s_n\}\subset [0,\mathrm{\infty })$ be two sequences such that $\{t_n\}\to 0$ and $s_n\le \phi (t_n)$ for all n. Also assume that if $t_n=0$, then $s_n=0$. Hence $\{s_n\}\to 0$.

Proof (1) It is the same proof of item 2 of Lemma 2.3.

(2) It follows from the fact that $s_n\le \phi (t_n)<t_n$ if $t_n>0$, and $s_n=0$ if $t_n=0$. In any case, $s_n\le t_n$ for all n. □

Remark 2.4 The difference between items 2 and 3 of Lemma 2.3 and items 1 and 2 of Lemma 2.4 is important. If we assume that $\phi \in \mathrm{\Psi }$ and $t_{m+1}\le \phi (t_m)$ for all m, then it is impossible to deduce that $\{t_m\}\to 0$ or $\{\phi (t_m)\}\to 0$ in item 1 of the previous result. For instance, define $\phi (t)=t/2$ if $t>0$, and $\phi (0)=1/2$. Then $\phi \in \mathrm{\Psi }$ and the sequence $\{t_m\}=\{0,1/2,0,1/2,0,1/2,\dots \}$ verifies $t_{m+1}\le \phi (t_m)$ for all m but it does not converge.

3 Coincidence point theorems on quasi-metric spaces without the mixed monotone property

In this section, we present some coincidence point theorems in the framework of quasi-metric spaces under very general conditions which can be extended to the coupled case and can be applied to mappings that have not necessarily the mixed monotone property.

3.1 Basic notions depending on a subset ℳ

Definition 3.1 (See Kutbi et al. [5])

We say that a nonempty subset ℳ of $X^2$ is:

• reflexive if $(x,x)\in \mathcal{M}$ for all $x\in X$;

• antisymmetric if $x=y$ for all $x,y\in X$ such that $(x,y),(y,x)\in \mathcal{M}$;

• transitive if $(x,z)\in \mathcal{M}$ for all $x,y,z\in X$ such that $(x,y),(y,z)\in \mathcal{M}$.

Given two mappings $T,g:X\to X$, we say that ℳ is:

• g-transitive if $(gx,gz)\in \mathcal{M}$ for all $x,y,z\in X$ such that $(gx,gy),(gy,gz)\in \mathcal{M}$;

• g-closed if $(gx,gy)\in \mathcal{M}$ for all $x,y\in X$ such that $(x,y)\in \mathcal{M}$;

• $(T,g)$ -closed if $(Tx,Ty)\in \mathcal{M}$ for all $x,y\in X$ such that $(gx,gy)\in \mathcal{M}$;

• $(T,g)$ -compatible if $Tx=Ty$ for all $x,y\in X$ such that $gx=gy$ and $(gx,gy)\in \mathcal{M}$.

Clearly, every transitive subset is also g-transitive. Moreover, ℳ is g-closed if and only if it is $(g,I_X)$-closed, where $I_X$ denotes the identity mapping on X. The following lemma shows a simple way to consider g-transitive, $(T,g)$-closed sets.

Lemma 3.1 Given a binary relation ≼ on X, let us consider ${\mathcal{M}}_{\preccurlyeq }=\{(x,y)\in X^2:x\preccurlyeq y\}$, and let $T,g:X\to X$ be two mappings.

• 1. If ≼ is a preorder on X, then ${\mathcal{M}}_{\preccurlyeq }$ is reflexive, transitive and g-transitive.

• 2. If ≼ is a partial order on X, then ${\mathcal{M}}_{\preccurlyeq }$ is reflexive, transitive, antisymmetric and g-transitive.

• 3. ${\mathcal{M}}_{\preccurlyeq }$ is g-closed if and only if g is ≼-nondecreasing.

• 4. ${\mathcal{M}}_{\preccurlyeq }$ is $(T,g)$-closed if and only if T is $(g,\preccurlyeq )$-nondecreasing.

• 5. If ≼ is a partial order on X and ${\mathcal{M}}_{\preccurlyeq }$ is $(T,g)$-closed, then ${\mathcal{M}}_{\preccurlyeq }$ is $(T,g)$-compatible.

Proof First four properties are obvious. We prove the last one. Since T is $(g,\preccurlyeq )$-nondecreasing,

$$gx=gy\Rightarrow \left\{\begin{array}{c}gx\preccurlyeq gy\\ gy\preccurlyeq gx\end{array}\right\}\Rightarrow \left\{\begin{array}{c}Tx\preccurlyeq Ty\\ Ty\preccurlyeq Tx\end{array}\right\}\Rightarrow Tx=Ty.$$

 □

It is convenient to highlight that the notion of g-transitive, $(T,g)$-closed, nonempty subset $\mathcal{M}\subseteq X^2$ is more general than the idea of nondecreasing mapping on a preordered space (following the previous lemma), as we show in the following example.

Example 3.1 Let $X=[0,\mathrm{\infty })$ and let us define $T,g:X\to X$ by $gx=x+3$ and $Tx=x+4$ for all $x\in X$. Let ℳ be the subset

$$\mathcal{M}=\{(x,y)\in X^2:3\le x\le y\}\cup \{(0,1),(1,0),(1,2)\}.$$

Then ℳ does not come from a preorder (or a partial order) on X because it is not reflexive ($(0,0)\notin \mathcal{M}$), nor transitive ($(0,1),(1,2)\in \mathcal{M}$ but $(0,2)\notin \mathcal{M}$) nor antisymmetric ($(0,1),(0,1)\in \mathcal{M}$ but $0\ne 1$). However, ℳ is g-transitive and $(T,g)$-closed.

In the following definitions, we will use sequences $\{x_n\}\subseteq X$ such that $(x_n,x_m)\in \mathcal{M}$ for all $n,m\in \mathbb{N}$ with $n<m$. In this sense, the following notions must be called ‘right-notions’ because the same concepts could also be introduced involving sequences $\{x_n\}\subseteq X$ such that $(x_n,x_m)\in \mathcal{M}$ for all $n,m\in \mathbb{N}$ with $n>m$ (in this case, they would be ‘left-notions’). Then we could talk about $(T,g,\mathcal{M})$ -right-Picard sequences, ℳ-right-continuity, $(O,\mathcal{M})$ -right-compatibility and right-regularity. However, we advice the reader that, in order not to complicate the notation, we will omit the term ‘right’.

Definition 3.2 Let $(X,q)$ be a quasi-metric space, let ℳ be a nonempty subset of $X^2$, and let $T:X\to X$ be a mapping. We say that T is ℳ-continuous if $\{T{x}_n\}\stackrel{q}{⟶}Tu$ for all sequences $\{x_n\}\subseteq X$ such that $\{x_n\}\stackrel{q}{⟶}u\in X$ and $(x_n,x_m)\in \mathcal{M}$ for all $n,m\in \mathbb{N}$ with $n<m$.

Remark 3.1 Every continuous mapping from a quasi-metric space into itself is also ℳ-continuous, whatever the subset ℳ.

Definition 3.3 Let $T,g:X\to X$ be two mappings, let ${\{x_n\}}_{n\ge 0}\subseteq X$ be a sequence, and let ℳ be a nonempty subset of $X^2$. We say that $\{x_n\}$ is a:

• $(T,g)$ -Picard sequence if

  $$g{x}_{n+1}=T{x}_n\text{for all }n\ge 0;$$

  (3)

• $(T,g,\mathcal{M})$ -Picard sequence if it is a $(T,g)$-Picard sequence and

  $$(g{x}_n,g{x}_m)\in \mathcal{M}\text{for all }n,m\in {\mathbb{N}}_0\text{ such that }n<m.$$

  (4)

Lemma 3.2 Let $T,g:X\to X$ be two mappings.

• 1. If $T(X)\subseteq g(X)$, then there exists a $(T,g)$-Picard sequence based on each $x_0\in X$.

• 2. If ℳ is a g-transitive, $(T,g)$-closed, nonempty subset of $X^2$, then every $(T,g)$-Picard sequence ${\{x_n\}}_{n\ge 0}$ such that $(g{x}_0,T{x}_0)\in \mathcal{M}$ is a $(T,g,\mathcal{M})$-Picard sequence.

Proof (1) Let $x_0\in X$ be arbitrary. Since $T{x}_0\in T(X)\subseteq g(X)$, then there exists $x_1\in X$ such that $g{x}_1=T{x}_0$. Similarly, since $T{x}_1\in T(X)\subseteq g(X)$, then there exists $x_2\in X$ such that $g{x}_2=T{x}_1$. Repeating this argument by induction, we may consider a $(T,g)$-Picard sequence $\{x_n\}$ based on $x_0$.

(2) Assume that ${\{x_n\}}_{n\ge 0}$ is a $(T,g)$-Picard sequence such that $(g{x}_0,T{x}_0)\in \mathcal{M}$. Since $(g{x}_0,g{x}_1)=(g{x}_0,T{x}_0)\in \mathcal{M}$ and ℳ is $(T,g)$-closed, then $(T{x}_0,T{x}_1)\in \mathcal{M}$, which means that $(g{x}_1,g{x}_2)\in \mathcal{M}$. By induction, it follows that $(g{x}_n,g{x}_{n+1})\in \mathcal{M}$ for all $n\ge 0$. And using that ℳ is g-transitive, we deduce that

$$(g{x}_n,g{x}_{n+1}),(g{x}_{n+1},g{x}_{n+2}),\dots ,(g{x}_{m-1},g{x}_m)\in \mathcal{M}\Rightarrow (g{x}_n,g{x}_m)\in \mathcal{M}$$

for all $n,m\in \mathbb{N}$ such that $n<m$. □

The following definition extends some ideas that can be found in [17–19].

Definition 3.4 Let $(X,q)$ be a quasi-metric space, and let ℳ be a nonempty subset of $X^2$. Two mappings $T,g:X\to X$ are said to be $(O,\mathcal{M})$ -compatible if

$$\underset{m\to \mathrm{\infty }}{lim}q(gT{x}_m,Tg{x}_m)=0\text{and}\underset{m\to \mathrm{\infty }}{lim}q(Tg{x}_m,gT{x}_m)=0$$

provided that $\{x_m\}$ is a sequence in X such that $(g{x}_n,g{x}_m)\in \mathcal{M}$ for all $n<m$ and

$$\underset{m\to \mathrm{\infty }}{lim}T{x}_m=\underset{m\to \mathrm{\infty }}{lim}g{x}_m\in X.$$

Similarly, T and g are said to be $(O^{\prime },\mathcal{M})$ -compatible if

$$\underset{m\to \mathrm{\infty }}{lim}q(gT{x}_m,Tg{x}_m)=0\text{or}\underset{m\to \mathrm{\infty }}{lim}q(Tg{x}_m,gT{x}_m)=0$$

provided that $\{x_m\}$ is a sequence in X such that $(g{x}_n,g{x}_m)\in \mathcal{M}$ for all $n<m$ and

$$\underset{m\to \mathrm{\infty }}{lim}T{x}_m=\underset{m\to \mathrm{\infty }}{lim}g{x}_m\in X.$$

Clearly, if T and g are commuting, then they are both $(O,\mathcal{M})$-compatible or $(O^{\prime },\mathcal{M})$-compatible. The following notion also extends the regularity of an ordered metric space.

Definition 3.5 Let $(X,q)$ be a quasi-metric space, and let $A\subseteq X$ and $\mathcal{M}\subseteq X^2$ be two nonempty subsets. We say that $(A,q,\mathcal{M})$ is regular (or A is $(q,\mathcal{M})$ -regular) if we have that $(x_n,u)\in \mathcal{M}$ for all n provided that $\{x_n\}$ is a q-convergent sequence on A, $u\in A$ is its q-limit and $(x_n,x_m)\in \mathcal{M}$ for all $n<m$.

3.2 Coincidence point theorems using $(g,\mathcal{M},\mathrm{\Phi })$-contractions of the first kind

Next, we present the kind of contractions we will use.

Definition 3.6 Let $(X,q)$ be a quasi-metric space, let $T,g:X\to X$ be two mappings, and let $\mathcal{M}\subseteq X^2$ be a nonempty subset of $X^2$. We say that T is a $(g,\mathcal{M},\mathrm{\Phi })$ -contraction of the first kind if there exist $\phi ,{\phi }^{\prime }\in \mathrm{\Phi }$ such that

$$q(Tx,Ty)\le \phi (q(gx,gy))\text{and}$$

(5)

$$q(Ty,Tx)\le {\phi }^{\prime }(q(gy,gx))$$

(6)

for all $x,y\in X$ such that $(gx,gy)\in \mathcal{M}$. If $\phi ,{\phi }^{\prime }\in \mathrm{\Psi }$, we say that T is a $(g,\mathcal{M},\mathrm{\Psi })$ -contraction of the first kind.

Remark 3.2 It is not necessary that functions in Φ and in Ψ verify all their properties in $[0,\mathrm{\infty })$. In fact, as we shall only use inequalities (5)-(6), the properties of functions in Φ and in Ψ must only be verified on the image of the quasi-metric q, that is, on $q(X\times X)\subseteq [0,\mathrm{\infty })$, which does not necessarily coincide with $[0,\mathrm{\infty })$ (for instance, if X is q-bounded).

Remark 3.3 One of the best advantages of using a subset $\mathcal{M}\subseteq X^2$ is that a unique condition covers two particularly interesting cases:

• $\mathcal{M}=X^2$, in which contractivity conditions (5)-(6) hold for all $x,y\in X$; and

• $\mathcal{M}={\mathcal{M}}_{\preccurlyeq }$, where ≼ is a preorder or a partial order on X, in which (5)-(6) must be assumed for all $x,y\in X$ such that $gx\preccurlyeq gy$.

Both possibilities were independently studied in the past, but this new vision unifies them in an only assumption.

The following one is a first property of this kind of mappings.

Lemma 3.3 Let $(X,q)$ be a quasi-metric space, let $T,g:X\to X$ be two mappings, and let $\mathcal{M}\subseteq X^2$ be a g-closed, nonempty subset of $X^2$ such that $(X,q,\mathcal{M})$ is regular. Suppose that, at least, one of the following conditions holds.

• 1. T is a $(g,\mathcal{M},\mathrm{\Phi })$-contraction of the first kind.

• 2. T is a $(g,\mathcal{M},\mathrm{\Psi })$-contraction of the first kind and ℳ is $(T,g)$-compatible.

Then T is ℳ-continuous at every point in which g is ℳ-continuous.

Proof Let $\{x_n\}\subseteq X$ be a sequence such that $\{x_n\}\stackrel{q}{⟶}z\in X$ and $(x_n,x_m)\in \mathcal{M}$ for all $n,m\in \mathbb{N}$ with $n<m$. Taking into account that g is ℳ-continuous at z, then $\{g{x}_n\}\stackrel{q}{⟶}gz$. As ℳ is g-closed, then $(g{x}_n,g{x}_m)\in \mathcal{M}$ for all $n,m\in \mathbb{N}$ with $n<m$. Furthermore, as $(X,q,\mathcal{M})$ is regular, then $(g{x}_n,gz)\in \mathcal{M}$ for all $n\in \mathbb{N}$. Applying the contractivity conditions (5)-(6), we have that, for all n,

$$q(T{x}_n,Tz)\le \phi (q(g{x}_n,gz))\text{and}q(Tz,T{x}_n)\le {\phi }^{\prime }(q(gz,g{x}_n)).$$

If $\phi ,{\phi }^{\prime }\in \mathrm{\Phi }$, then item 3 of Lemma 2.3 guarantees that $\{q(T{x}_n,Tz)\}\to 0$ and $\{q(Tz,T{x}_n)\}\to 0$, so $\{T{x}_n\}$ q-converges to Tz. If $\phi ,{\phi }^{\prime }\in \mathrm{\Psi }$ and we additionally assume that ℳ is $(T,g)$-compatible, we can use item 2 of Lemma 2.4 applied to the sequences $\{t_n=q(T{x}_n,Tz)\}$ and $\{s_n=q(g{x}_n,gz)\}$ in order to deduce that $\{q(T{x}_n,Tz)\}\to 0$ (notice that if $s_n=0$, then $t_n=0$) and similarly $\{q(Tz,T{x}_n)\}\to 0$. □

The first main result of this work is the following one.

Theorem 3.1 Let $(X,q)$ be a quasi-metric space, let $T,g:X\to X$ be two mappings, and let ℳ be a nonempty subset of $X^2$. Suppose that the following conditions are fulfilled.

• (A) There exists a $(T,g,\mathcal{M})$-Picard sequence on X.

• (B) T is a $(g,\mathcal{M},\mathrm{\Phi })$-contraction of the first kind.

Also assume that, at least, one of the following conditions holds.

• (a) X (or $g(X)$ or $T(X)$) is q-complete, T and g are ℳ-continuous and the pair $(T,g)$ is $(O^{\prime },\mathcal{M})$-compatible;

• (b) X (or $g(X)$ or $T(X)$) is q-complete and T and g are ℳ-continuous and commuting;

• (c) $(g(X),q)$ is complete and X (or $g(X)$) is $(q,\mathcal{M})$-regular;

• (d) $(X,q)$ is complete, $g(X)$ is closed and X (or $g(X)$) is $(q,\mathcal{M})$-regular;

• (e) $(X,q)$ is complete, g is ℳ-continuous, ℳ is g-closed, the pair $(T,g)$ is $(O,\mathcal{M})$-compatible and X is $(q,\mathcal{M})$-regular.

Then T and g have, at least, a coincidence point.

Notice that, by Lemma 3.2, the previous result also holds if we replace condition (A) by one of the following stronger hypotheses:

(${\mathrm{A}}^{\prime }$) $T(X)\subseteq g(X)$ and ℳ is g-transitive and $(T,g)$-closed.

(${\mathrm{A}}^{″}$) ℳ is g-transitive and $(T,g)$-closed, and there exists a $(T,g)$-Picard sequence ${\{x_n\}}_{n\ge 0}$ such that $(g{x}_0,T{x}_0)\in \mathcal{M}$.

And by Remark 3.1, the ℳ-continuity of the mappings can be replaced by continuity.

Proof Let $\{x_n\}$ be an arbitrary $(T,g,\mathcal{M})$-Picard sequence on X, and let $\phi ,{\phi }^{\prime }\in \mathrm{\Phi }$ be such that (5)-(6) hold. If there exists some $n_0\in \mathbb{N}$ such that $g{x}_{n_0}=g{x}_{n_0+1}$, then $g{x}_{n_0}=g{x}_{n_0+1}=T{x}_{n_0}$, so $x_{n_0}$ is a coincidence point of T and g, and the proof is finished. On the contrary, assume that $g{x}_n\ne g{x}_{n+1}$ for all $n\ge 0$. Therefore,

$$q(g{x}_n,g{x}_{n+1})>0\text{and}q(g{x}_{n+1},g{x}_n)>0\text{for all }n\ge 0.$$

(7)

Step 1. We claim that ${lim}_{n\to \mathrm{\infty }}q(g{x}_n,g{x}_{n+1})={lim}_{n\to \mathrm{\infty }}q(g{x}_{n+1},g{x}_n)=0$. Taking into account (4), if we apply the contractivity condition (5) to $x=g{x}_{n+1}$ and $y=g{x}_{n+2}$, we obtain that

$$q(g{x}_{n+1},g{x}_{n+2})=q(T{x}_n,T{x}_{n+1})\le \phi (q(g{x}_n,g{x}_{n+1}))\text{for all }n\ge 0.$$

By item 2 of Lemma 2.3, we have that $\{q(g{x}_n,g{x}_{n+1})\}\to 0$. Similarly, using $x=g{x}_{n+2}$ and $y=g{x}_{n+1}$ and the contractivity condition (6), we could deduce that $\{q(g{x}_{n+1},g{x}_n)\}\to 0$. Therefore, we have proved that

$$\underset{n\to \mathrm{\infty }}{lim}q(g{x}_n,g{x}_{n+1})=\underset{n\to \mathrm{\infty }}{lim}q(g{x}_{n+1},g{x}_n)=0.$$

(8)

Step 2. We claim that $\{g{x}_n\}$ is right-Cauchy in $(X,q)$, that is, for all $\epsilon >0$, there is $n_0\in N$ such that $q(g{x}_n,g{x}_m)\le \epsilon$ for all $m>n\ge n_0$ . We reason by contradiction. If $\{g{x}_n\}$ is not right-Cauchy, there exist ${\epsilon }_0>0$ and two subsequences ${\{g{x}_{n(k)}\}}_{k\in {\mathbb{N}}_0}$ and ${\{g{x}_{m(k)}\}}_{k\in {\mathbb{N}}_0}$ verifying that

$$k\le n(k)<m(k),q(g{x}_{n(k)},g{x}_{m(k)})>{\epsilon }_0\text{for all }k.$$

(9)

Taking $m(k)$ as the smallest integer, greater than $n(k)$, verifying this property, we can suppose that

$$q(g{x}_{n(k)},g{x}_{m(k)-1})\le {\epsilon }_0\text{for all }k.$$

Therefore ${\epsilon }_0<q(g{x}_{n(k)},g{x}_{m(k)})\le q(g{x}_{n(k)},g{x}_{m(k)-1})+q(g{x}_{m(k)-1},g{x}_{m(k)})\le {\epsilon }_0+q(g{x}_{m(k)-1},g{x}_{m(k)})$, and taking limit as $k\to \mathrm{\infty }$, it follows from (8) that

$$\underset{k\to \mathrm{\infty }}{lim}q(g{x}_{n(k)},g{x}_{m(k)})={\epsilon }_0.$$

Notice that, for all k,

$$q(g{x}_{n(k)+1},g{x}_{m(k)+1})\le q(g{x}_{n(k)+1},g{x}_{n(k)})+q(g{x}_{n(k)},g{x}_{m(k)})+q(g{x}_{m(k)},g{x}_{m(k)+1}),$$

and

$${\epsilon }_0<q(g{x}_{n(k)},g{x}_{m(k)})\le q(g{x}_{n(k)},g{x}_{n(k)+1})+q(g{x}_{n(k)+1},g{x}_{m(k)+1})+q(g{x}_{m(k)+1},g{x}_{m(k)}).$$

Joining both inequalities we deduce that, for all k,

$$\begin{array}{r}{\epsilon }_0-q(g{x}_{n(k)},g{x}_{n(k)+1})-q(g{x}_{m(k)+1},g{x}_{m(k)})\\ \le q(g{x}_{n(k)+1},g{x}_{m(k)+1})\le q(g{x}_{n(k)+1},g{x}_{n(k)})+q(g{x}_{n(k)},g{x}_{m(k)})+q(g{x}_{m(k)},g{x}_{m(k)+1}).\end{array}$$

Letting $k\to \mathrm{\infty }$, it follows from (8) that

$$\underset{k\to \mathrm{\infty }}{lim}q(g{x}_{n(k)+1},g{x}_{m(k)+1})={\epsilon }_0.$$

(10)

Next, let us apply the contractivity condition (5) to $x=g{x}_{n(k)}$ and $y=g{x}_{m(k)}$, taking into account that, by (7), $(g{x}_{n(k)},g{x}_{m(k)})\in \mathcal{M}$. We get that, for all $k\ge 0$,

$$q(g{x}_{n(k)+1},g{x}_{m(k)+1})=q(T{x}_{n(k)},T{x}_{m(k)})\le \phi (q(g{x}_{n(k)},g{x}_{m(k)})).$$

(11)

Since $q(g{x}_{n(k)},g{x}_{m(k)})>{\epsilon }_0$ for all n, $\{q(g{x}_{n(k)},g{x}_{m(k)})\}\to {\epsilon }_0$ and $\phi \in \mathrm{\Phi }$, then

$$\underset{k\to \mathrm{\infty }}{lim}\phi (q(g{x}_{n(k)},g{x}_{m(k)}))=\underset{s\to {\epsilon }_0^{+}}{lim}\phi (s)<{\epsilon }_0.$$

(12)

Letting $k\to \mathrm{\infty }$ in (11) and taking into account (10) and (12), it follows that

$${\epsilon }_0=\underset{k\to \mathrm{\infty }}{lim}q(g{x}_{n(k)+1},g{x}_{m(k)+1})\le \underset{k\to \mathrm{\infty }}{lim}\phi (q(g{x}_{n(k)},g{x}_{m(k)}))<{\epsilon }_0,$$

which is a contradiction. This contradiction ensures us that $\{g{x}_n\}$ is right-Cauchy in $(X,q)$, and Step 2 holds.

Similarly, using the contractivity condition (6), it can be proved that $\{g{x}_n\}$ is left-Cauchy in $(X,q)$, so we conclude that $\{g{x}_n\}$ is a Cauchy sequence in $(X,q)$. Now, we prove that T and g have a coincidence point distinguishing between cases (a)-(e).

Case (a): X (or $g(X)$ or $T(X)$) is q-complete, T and g are ℳ-continuous and the pair $(T,g)$ is $(O^{\prime },\mathcal{M})$ -compatible. As $(X,q)$ is complete, there exists $u\in X$ such that $\{g{x}_n\}\to u$ (notice that as $\{g{x}_{n+1}\}=\{T{x}_n\}\subset g(X)\cap T(X)$, then this property also occurs if $g(X)$ or $T(X)$ is q-complete). As T and g are ℳ-continuous, it follows from (4) that $\{Tg{x}_n\}\to Tu$ and $\{gg{x}_n\}\to gu$. Taking into account that the pair $(T,g)$ is $(O^{\prime },\mathcal{M})$-compatible, we deduce that

$$\underset{m\to \mathrm{\infty }}{lim}q(gT{x}_m,Tg{x}_m)=0\text{or}\underset{m\to \mathrm{\infty }}{lim}q(Tg{x}_m,gT{x}_m)=0.$$

In such a case, using item 2 of Remark 2.3, we conclude that

$$q(gu,Tu)=\underset{n\to \mathrm{\infty }}{lim}q(gg{x}_{n+1},Tg{x}_n)=\underset{n\to \mathrm{\infty }}{lim}q(gT{x}_n,Tg{x}_n)=0$$

(the other case is similar). Hence, u is a coincidence point of T and g.

Case (b): X (or $g(X)$ or $T(X)$) is q-complete and T and g are ℳ-continuous and commuting. It is obvious because (b) implies (a).

Case (c): $(g(X),q)$ is complete and X (or $g(X)$) is $(q,\mathcal{M})$ -regular. As $\{g{x}_m\}$ is a Cauchy sequence in the complete space $(g(X),q)$, there is $u\in g(X)$ such that $\{g{x}_m\}\to u$. Let $v\in X$ be any point such that $u=gv$. In this case, $\{g{x}_m\}\to gv$. We are also going to show that $\{g{x}_m\}\to Tv$, so we will conclude that $gv=Tv$ (and v is a coincidence point of T and g).

Indeed, as $\{g{x}_n\}$ is a convergent sequence in $g(X)$ such that $(g{x}_n,g{x}_m)\in \mathcal{M}$ for all $n<m$, and X (or $g(X)$) is $(q,M)$-regular, then $(g{x}_n,gv)\in \mathcal{M}$ for all n, where $gv=u\in g(X)$ is the limit of $\{g{x}_n\}$. Applying the contractivity conditions (5)-(6),

$$q(g{x}_{n+1},Tv)=q(T{x}_n,Tv)\le \phi (q(g{x}_n,gv))\text{and}$$

(13)

$$q(Tv,g{x}_{n+1})=q(Tv,T{x}_n)\le \phi (q(gv,g{x}_n))\text{for all }n\ge 0.$$

(14)

By item 3 of Lemma 2.3, $\{g{x}_n\}$ q-converges to Tv.

Case (d): $(X,q)$ is complete, $g(X)$ is closed and X (or $g(X)$) is $(q,\mathcal{M})$ -regular. It follows from the fact that a closed subset of a complete quasi-metric space is also complete. Then $(g(X),q)$ is complete and case (c) is applicable.

Case (e): $(X,q)$ is complete, g is ℳ-continuous, ℳ is g-closed, the pair $(T,g)$ is $(O,\mathcal{M})$ -compatible and X is $(q,\mathcal{M})$ -regular. As $(X,q)$ is complete, there exists $u\in X$ such that $\{g{x}_m\}\to u$. As $T{x}_m=g{x}_{m+1}$ for all m, we also have that $\{T{x}_m\}\to u$. As g is ℳ-continuous and $(g{x}_n,g{x}_m)\in \mathcal{M}$ for all $n<m$, then $\{gg{x}_m\}\to gu$. Furthermore, as the pair $(T,g)$ is $(O,\mathcal{M})$-compatible, then

$$\begin{array}{r}\underset{m\to \mathrm{\infty }}{lim}q(gg{x}_{m+1},Tg{x}_m)=\underset{m\to \mathrm{\infty }}{lim}q(gT{x}_m,Tg{x}_m)=0\text{and}\\ \underset{m\to \mathrm{\infty }}{lim}q(Tg{x}_m,gg{x}_{m+1})=\underset{m\to \mathrm{\infty }}{lim}q(Tg{x}_m,gT{x}_m)=0.\end{array}$$

By item 3 of Remark 2.3, as $\{gg{x}_m\}\to gu$, the previous properties imply that $\{Tg{x}_m\}\to gu$. We are going to show that $\{Tg{x}_m\}\to Tu$ and this finishes the proof.

Indeed, since X is $(q,\mathcal{M})$-regular, $\{g{x}_m\}\to u$ and $(g{x}_n,g{x}_m)\in \mathcal{M}$ for all $n<m$, then $(g{x}_n,u)\in \mathcal{M}$ for all n. Moreover, taking into account that ℳ is g-closed, then $(gg{x}_n,gu)\in \mathcal{M}$ for all n. Applying the contractivity conditions (5)-(6),

$$q(Tg{x}_n,Tu)\le \phi (q(gg{x}_n,gu))\text{and}$$

(15)

$$q(Tu,Tg{x}_n)\le \phi (q(gu,gg{x}_n))\text{for all }n\ge 0.$$

(16)

As $\{gg{x}_n\}\to gu$, then $\{Tg{x}_n\}\to Tu$. □

Example 3.2 To illustrate the applicability of Theorem 3.1, we show the following example in which mappings are nonlinear. Let $X=\mathbb{R}$ and let

$$\mathcal{M}=\{(x,x):x\in \mathbb{R}\}\cup \{(x,y):0\le y<x\le 1\}\cup \{(9,16),(16,9)\}\subset {\mathbb{R}}^2.$$

Clearly, ℳ does not come from any partial order on X as in Lemma 3.1 because it is not antisymmetric: $(9,16),(16,9)\in \mathcal{M}$ but $9\ne 16$. Let us consider on X the function $q:X\times X\to [0,\mathrm{\infty })$ given, for all $x,y\in X$, by

$$q(x,y)=\{\begin{array}{ll}y-x,& \text{if }x\le y,\\ 2(x-y),& \text{if }x>y.\end{array}$$

Then q is a complete quasi-metric on ℝ. In fact, it has the same convergent sequences to the same limits as the Euclidean metric $d(x,y)=|x-y|$ for all $x,y\in \mathbb{R}$ because

$$|x-y|\le q(x,y)\le 2|x-y|\le 2q(x,y)\text{for all }x,y\in \mathbb{R}.$$

However, q is not a metric because $q(1,2)\ne q(2,1)$.

Now, given a real number $\lambda \in (0.5,1)$, let us consider the mappings $T,g:\mathbb{R}\to \mathbb{R}$ defined, for all $x\in \mathbb{R}$, by

$$Tx=\{\begin{array}{ll}{x}^2,& \text{if }x<0\\ \lambda x,& \text{if }0\le x\le 1,\\ x,& \text{if }x>1,\end{array}gx=\{\begin{array}{ll}-x^2,& \text{if }x<0\\ x,& \text{if }0\le x\le 1,\\ x^2,& \text{if }x>1.\end{array}$$

Also consider the function ${\phi }_{\lambda }:[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ defined by ${\phi }_{\lambda }(t)=\lambda t$ for all $t\in [0,\mathrm{\infty })$. Clearly, ${\phi }_{\lambda }\in \mathrm{\Phi }\cap \mathrm{\Psi }$. We are going to show that Theorem 3.1 is applicable to the previous setting, because the previous properties hold.

• 1. The sequence $\{x_n\}$, given by $x_n={\lambda }^n$ for all $n\in {\mathbb{N}}_0$, is a $(T,g,\mathcal{M})$-Picard sequence.

• 2. The function $g:\mathbb{R}\to \mathbb{R}$ is bijective and nondecreasing.

• 3. The range of g, which is $g(X)=\mathbb{R}$, is closed and complete in $(\mathbb{R},q)$.

• 4. We claim that T is a $(g,\mathcal{M},\mathrm{\Phi })$-contraction of the first kind. To prove it, let $x,y\in X$ be such that $(gx,gy)\in \mathcal{M}$. If $Tx=Ty$, then (5)-(6) are obvious. Next, assume that $Tx\ne Ty$. In particular, $x\ne y$. Hence, $gx\ne gy$ because g is bijective. Therefore, the condition $(gx,gy)\in \mathcal{M}$ leads to two cases.

• If $0\le gy<gx\le 1$, then $0\le y<x\le 1$. Therefore

  $$\begin{array}{r}q(Tx,Ty)=q(\lambda x,\lambda y)=2\lambda (y-x)={\phi }_{\lambda }(2(y-x))={\phi }_{\lambda }(q(x,y));\\ q(Ty,Tx)=q(\lambda x,\lambda y)=\lambda (y-x)={\phi }_{\lambda }(y-x)={\phi }_{\lambda }(q(y,x)).\end{array}$$

• If $\{gx,gy\}=\{9,16\}$, then $\{x,y\}=\{3,4\}$. In such a case,

  $$\begin{array}{r}q(T3,T4)=q(3,4)=1<7\lambda =\lambda q(9,16)={\phi }_{\lambda }(q(g3,g4));\\ q(T4,T3)=q(4,3)=2<14\lambda =\lambda q(16,9)={\phi }_{\lambda }(q(g4,g3)).\end{array}$$

• 5. Let $\{x_n\}\subset \mathbb{R}$ be a sequence such that $(x_n,x_{n+1})\in \mathcal{M}$ for all $n\in {\mathbb{N}}_0$. Then one, and only one, of the following cases holds.

(5.a) There exists $n_0\in \mathbb{N}$ such that $x_{n_0}\in [0,1]$. In this case, $x_n\in [0,1]$ and $x_{n+1}\le x_n$ for all $n\in {\mathbb{N}}_0$.

To prove it, notice that $(x_{n_0},x_{n_0+1})\in \mathcal{M}$ is only possible when $x_{n_0}=x_{n_0+1}$ or $0\le x_{n_0+1}<x_{n_0}\le 1$. In any case, $x_{n_0+1}\in [0,1]$. Repeating this argument, $x_n\in [0,1]$ for all $n\ge n_0$. But if $n_0-1\in \mathbb{N}$, the condition $(x_{n_0-1},x_{n_0})\in \mathcal{M}$ also leads to $x_{n_0-1}\in [0,1]$. And we can again repeat the argument.

(5.b) There exists $n_0\in \mathbb{N}$ such that $x_{n_0}\in \{9,16\}$. In this case, $x_n\in \{9,16\}$ for all $n\in {\mathbb{N}}_0$.

(5.c) There exists $z\in \mathbb{R}\mathrm{╲}([0,1]\cup \{9,16\})$ such that $x_n=z$ for all $\in {\mathbb{N}}_0$. In this case, $\{x_n\}$ is a constant sequence.

• 6. The range $g(X)=\mathbb{R}$ is $(q,\mathcal{M})$-regular. To prove it, let $u\in \mathbb{R}$ and let $\{x_n\}\subset \mathbb{R}$ be a sequence such that$\{x_n\}\stackrel{q}{\to }u$ and $(x_n,x_{n+1})\in \mathcal{M}$ for all $n\in {\mathbb{N}}_0$. In particular, $\{x_n\}\to u$ using the Euclidean metric. We can distinguish the previous three cases.

(6.a) Suppose that $x_n\in [0,1]$ and $x_{n+1}\le x_n$ for all $n\in {\mathbb{N}}_0$. Therefore, $u\in [0,1]$ and $u\le x_{n+1}\le x_n$ for all $n\in {\mathbb{N}}_0$, so $(x_n,u)\in \mathcal{M}$ for all $n\in {\mathbb{N}}_0$.

(6.b) Suppose that $x_n\in \{9,16\}$ for all $n\in {\mathbb{N}}_0$. Then $u\in \{9,16\}$ and, therefore, $(x_n,u)\in \mathcal{M}$ for all $n\in {\mathbb{N}}_0$.

(6.c) Suppose that $x_n=z\in \mathbb{R}\mathrm{╲}([0,1]\cup \{9,16\})$ for all $n\in {\mathbb{N}}_0$. Therefore $u=z$ and $(x_n,u)\in \mathcal{M}$ for all $n\in {\mathbb{N}}_0$.

The previous properties show that case (c) of Theorem 3.1 is applicable, so T and g have, at least, a coincidence point, which is $x=0$.

Notice that T and g do not satisfy the condition

$$q(Tx,Ty)\le \phi (q(gx,gy))\text{for all }x,y\in X$$

because if $x=-2$ and $y=-1$, then

$$q(T(-2),T(-1))=q(4,1)=6>3=q(-4,-1)=q(g(-2),g(-1)).$$

We extend the previous theorem to the case in which $\phi \in \mathrm{\Psi }$.

Theorem 3.2 If we additionally assume that ℳ is $(T,g)$-compatible, then Theorem  3.1 also holds even if T is a $(g,\mathcal{M},\mathrm{\Psi })$-contraction of the first kind.

Proof We can follow, point by point, the proof of the previous result and obtain inequalities (13)-(14). In this case, we cannot use Lemma 2.3, but we may use the fact that ℳ is $(T,g)$-compatible. Therefore, we know that, as $(g{x}_n,gv)\in \mathcal{M}$ for all n, then

$$q(g{x}_n,gv)=0\Rightarrow g{x}_n=gv\Rightarrow T{x}_n=Tv\Rightarrow q(g{x}_{n+1},Tv)=q(T{x}_n,Tv)=0.$$

By item 2 of Lemma 2.4 we conclude that $\{q(g{x}_{n+1},Tv)\}\to 0$. In the same way, $\{q(Tv,g{x}_{n+1})\}\to 0$, so $\{g{x}_n\}$ q-converges to Tv.

The same argument is valid when applied to inequalities (15)-(16). □

3.3 Coincidence point theorems using $(g,\mathcal{M},\mathrm{\Phi })$-contractions of the second kind

Many results on fixed point theory in the setting of G-metrics can be similarly proved using the quasi-metrics $q_G$ and $q_G^{\prime }$ associated to G as in Lemma 2.2 (see, for instance, Agarwal et al. [9]). These families of quasi-metrics verify additional properties that are not true for an arbitrary quasi-metric. Using these properties, it is possible to relax some conditions on the kind of considered contractions, obtaining similar results. This is the case of the following kind of mappings.

Definition 3.7 Let $(X,q)$ be a quasi-metric space, let $T,g:X\to X$ be two mappings, and let $\mathcal{M}\subseteq X^2$ be a nonempty subset of $X^2$. We say that T is a $(g,\mathcal{M},\mathrm{\Phi })$ -contraction of the second kind if there exists $\phi \in \mathrm{\Phi }$ such that

$$q(Tx,Ty)\le \phi (q(gx,gy))$$

(17)

for all $x,y\in X$ such that $(gx,gy)\in \mathcal{M}$. If $\phi \in \mathrm{\Psi }$, we say that T is a $(g,\mathcal{M},\mathrm{\Psi })$ -contraction of the second kind.

Notice that condition (17) is not symmetric on x and y because $(gx,gy)\in \mathcal{M}$ does not imply $(gy,gx)\in \mathcal{M}$. In order to compensate this absence of symmetry, we will suppose an additional condition on the ambient space.

Definition 3.8 We say that a quasi-metric space $(X,q)$ is:

• right-Cauchy if every right-Cauchy sequence in $(X,q)$ is, in fact, a Cauchy sequence in $(X,q)$;

• left-Cauchy if every left-Cauchy sequence in $(X,q)$ is, in fact, a Cauchy sequence in $(X,q)$;

• right-convergent if every right-convergent sequence in $(X,q)$ is, in fact, a convergent sequence in $(X,q)$;

• left-convergent if every left-convergent sequence in $(X,q)$ is, in fact, a convergent sequence in $(X,q)$.

It is convenient not to confuse the previous notions with the concept of left/right complete quasi-metric space given in Definition 2.8. Lemma 2.2 guarantees that there exists a wide family of quasi-metrics that verify all the previous properties.

Corollary 3.1 Every quasi-metric $q_G$ and $q_G^{\prime }$ associated to a G-metric G on X is right and left-Cauchy and right and left-convergent.

Next we prove a similar result to Theorem 3.1. In this case, the contractivity condition is weaker but we suppose additional conditions on the ambient space.

Theorem 3.3 Let $(X,q)$ be a right-Cauchy quasi-metric space, let $T,g:X\to X$ be two mappings, and let ℳ be a nonempty subset of $X^2$. Suppose that the following conditions are fulfilled.

• (A) There exists a $(T,g,\mathcal{M})$-Picard sequence on X.

• (B) T is a $(g,\mathcal{M},\mathrm{\Phi })$-contraction of the second kind.

Also assume that, at least, one of the following conditions holds.

• (a) X (or $g(X)$ or $T(X)$) is q-complete, T and g are ℳ-continuous and the pair $(T,g)$ is $(O^{\prime },\mathcal{M})$-compatible;

• (b) X (or $g(X)$ or $T(X)$) is q-complete and T and g are ℳ-continuous and commuting;

• (c) $(g(X),q)$ is complete and right-convergent, and X (or $g(X)$) is $(q,\mathcal{M})$-regular;

• (d) $(X,q)$ is complete and right-convergent, $g(X)$ is closed and X (or $g(X)$) is $(q,\mathcal{M})$-regular;

• (e) $(X,q)$ is complete and right-convergent, g is ℳ-continuous, ℳ is g-closed, the pair $(T,g)$ is $(O,\mathcal{M})$-compatible and X is $(q,\mathcal{M})$-regular.

Then T and g have, at least, a coincidence point.

Notice that, by Lemma 3.2, the previous result also holds if we replace condition (A) by one of the following stronger hypotheses:

(${\mathrm{A}}^{\prime }$) $T(X)\subseteq g(X)$ and ℳ is g-transitive and $(T,g)$-closed.

(${\mathrm{A}}^{″}$) ℳ is g-transitive and $(T,g)$-closed, and there exists a $(T,g)$-Picard sequence ${\{x_n\}}_{n\ge 0}$ such that $(g{x}_0,T{x}_0)\in \mathcal{M}$.

And by Remark 3.1, the ℳ-continuity of the mappings can be replaced by continuity.

Proof We can follow, step by step, the lines of the proof of Theorem 3.1 to deduce, in the case $g{x}_n\ne g{x}_{n+1}$ for all $n\ge 0$, that $\{g{x}_n\}$ is right-Cauchy in $(X,q)$. Using that $(X,q)$ is right-Cauchy, then it is a Cauchy sequence in $(X,q)$. Now, we prove that T and g have a coincidence point distinguishing between cases (a)-(e). Cases (a) and (b) have the same proof as in Theorem 3.1.

Case (c): $(g(X),q)$ is complete and right-convergent, and X (or $g(X)$) is $(q,\mathcal{M})$ -regular. As $\{g{x}_m\}$ is a Cauchy sequence in the complete space $(g(X),q)$, there is $u\in g(X)$ such that $\{g{x}_m\}\to u$. Let $v\in X$ be any point such that $u=gv$. In this case, $\{g{x}_m\}\to gv$. We are also going to show that $\{g{x}_m\}\to Tv$, so we will conclude that $gv=Tv$ (and v is a coincidence point of T and g).

Indeed, as $\{g{x}_n\}$ is a convergent sequence in $g(X)$ such that $(g{x}_n,g{x}_m)\in \mathcal{M}$ for all $n<m$, and X (or $g(X)$) is $(q,M)$-regular, then $(g{x}_n,gv)\in \mathcal{M}$ for all n, where $gv=u\in g(X)$ is the limit of $\{g{x}_n\}$. Applying the contractivity condition (17),

$$q(g{x}_{n+1},Tv)=q(T{x}_n,Tv)\le \phi (q(g{x}_n,gv))\text{for all }n.$$

By item 3 of Lemma 2.3, we have that $\{q(g{x}_{n+1},Tv)\}\to 0$, which means that $\{g{x}_n\}$ right-converges to Tv. Since $(X,q)$ is right-convergent, then $\{g{x}_n\}$ is a convergent sequence in $(X,q)$, and by item 4 of Remark 2.3, it converges to Tv.

Case (d): $(X,q)$ is complete and right-convergent, $g(X)$ is closed and X (or $g(X)$) is $(q,\mathcal{M})$ -regular. It follows from the fact that a closed subset of a complete quasi-metric space is also complete. Then $(g(X),q)$ is complete and case (c) is applicable.

Case (e): $(X,q)$ is complete and right-convergent, g is ℳ-continuous, ℳ is g-closed, the pair $(T,g)$ is $(O,\mathcal{M})$ -compatible and X is $(q,\mathcal{M})$ -regular. It follows step by step as in case (e) of the proof of Theorem 3.1 but, replacing (15)-(16) by the only inequality

$$q(Tg{x}_n,Tu)\le \phi (q(gg{x}_n,gu))\text{for all }n\ge 0.$$

In this case, by item 3 of Lemma 2.3, we have that $\{q(Tg{x}_n,Tu)\}\to 0$, which means that $\{Tg{x}_n\}$ right-converges to Tu. Since $(X,q)$ is right-convergent, then $\{Tg{x}_n\}$ is a convergent sequence in $(X,q)$, and by item 4 of Remark 2.3, it converges to Tu. □

Example 3.3 Theorem 3.3 can also be applied to mappings given in Example 3.2 because $(\mathbb{R},q)$ is right-convergent.

Repeating the arguments of Theorem 3.2, we extend the previous theorem to the case in which $\phi \in \mathrm{\Psi }$.

Theorem 3.4 If we additionally assume that ℳ is $(T,g)$-compatible, then Theorem  3.3 also holds even if T is a $(g,\mathcal{M},\mathrm{\Psi })$-contraction of the second kind.

3.4 Consequences

The previous theorems admit a lot of different particular cases employing continuity, the condition $T(X)\subseteq g(X)$ and the case in which g is the identity mapping on X. We highlight the following one in which a partial order is involved. Preliminaries of the following result can be found in [20].

Corollary 3.2 (Al-Mezel et al. [20], Theorem 34)

Let $(X,d,\preccurlyeq )$ be an ordered metric space, and let $T,g:X\to X$ be two mappings such that the following properties are fulfilled.

• (i) $T(X)\subseteq g(X)$;

• (ii) T is monotone $(g,\preccurlyeq )$-nondecreasing;

• (iii) there exists $x_0\in X$ such that $g{x}_0\preccurlyeq T{x}_0$;

• (iv) there exists $\phi \in \mathrm{\Psi }$ verifying

  $$d(Tx,Ty)\le \phi (d(gx,gy))\mathit{\text{for all }}x,y\in X\mathit{\text{ such that }}gx\preccurlyeq gy.$$

Also assume that, at least, one of the following conditions holds.

• (a) $(X,d)$ is complete, T and g are continuous and the pair $(T,g)$ is O-compatible;

• (b) $(X,d)$ is complete and T and g are continuous and commuting;

• (c) $(g(X),d)$ is complete and $(X,d,\preccurlyeq )$ is nondecreasing-regular;

• (d) $(X,d)$ is complete, $g(X)$ is closed and $(X,d,\preccurlyeq )$ is nondecreasing-regular;

• (e) $(X,d)$ is complete, g is continuous and monotone ≼-nondecreasing, the pair $(T,g)$ is O-compatible and $(X,d,\preccurlyeq )$ is nondecreasing-regular.

Then T and g have, at least, a coincidence point.

Proof It is only necessary to apply Theorem 3.2 to the subset ${\mathcal{M}}_{\preccurlyeq }=\{(x,y)\in X^2:x\preccurlyeq y\}$, taking into account the properties given in Lemma 3.1. Notice that in case (e), we use Lemma 3.3 to avoid assuming that T is continuous. □

The following result improves the last one because we do not assume that T is ℳ-continuous in hypothesis (b).

Corollary 3.3 Let $(X,q)$ be a complete quasi-metric space, let $T,g:X\to X$ be two mappings such that $T(X)\subseteq g(X)$, and let ℳ be a g-transitive, $(T,g)$-closed, nonempty subset of $X^2$. Suppose that T is a $(g,\mathcal{M},\mathrm{\Phi })$-contraction (respectively, T is a $(g,\mathcal{M},\mathrm{\Psi })$-contraction and ℳ is $(T,g)$-compatible), g is ℳ-continuous, T and g are commuting and there exists $x_0\in X$ such that $(g{x}_0,T{x}_0)\in \mathcal{M}$. Also assume that, at least, one of the following conditions holds.

• (a) T is ℳ-continuous, or

• (b) ℳ is g-closed and $(X,q,\mathcal{M})$ is regular.

Then T and g have, at least, a coincidence point.

Proof We show that case (b) in Theorem 3.1 is applicable. By item 1 of Lemma 3.2, X contains a $(T,g)$-Picard sequence $\{x_n\}$ based on $x_0\in X$, and by item 2 of the same lemma, $\{x_n\}$ is a $(T,g,\mathcal{M})$-Picard sequence.

If T is ℳ-continuous, item (b) of Theorem 3.1 (and also Theorem 3.2 in the case of a $(g,\mathcal{M},\mathrm{\Psi })$-contraction) can be used to ensure that T and g have, at least, a coincidence point. In other case, if ℳ is g-closed and $(X,q,\mathcal{M})$ is regular, then Lemma 3.3 guarantees that T is ℳ-continuous. □

Another interesting particularization is the following one.

Corollary 3.4 (Karapınar et al. [7], Theorem 33)

Let $(X,d)$ be a complete metric space, let $T,g:X\to X$ be two mappings such that $TX\subseteq gX$, and let $M\subseteq X^2$ be a $(T,g)$-compatible, $(T,g)$-closed, transitive subset. Assume that there exists $\phi \in \mathrm{\Phi }$ such that

$$d(Tx,Ty)\le \phi (d(gx,gy))\mathit{\text{for all }}x,y\in X\mathit{\text{ such that }}(gx,gy)\in M.$$

(18)

Also assume that, at least, one of the following conditions holds.

• (a) T and g are M-continuous and $(O,M)$-compatible;

• (b) T and g are continuous and commuting;

• (c) $(X,d,M)$ is regular and gX is closed.

If there exists a point $x_0\in X$ such that $(g{x}_0,T{x}_0)\in M$, then T and g have, at least, a coincidence point.

As a consequence, in the following result, a partial order is not necessary.

Corollary 3.5 (Karapınar et al. [7], Corollary 35)

Let $(X,d)$ be a complete metric space, and let ≼ be a transitive relation on X. Let $T,g:X\to X$ be two mappings such that $TX\subseteq gX$ and T is $(g,\preccurlyeq )$-nondecreasing. Suppose that there exists $\phi \in \mathrm{\Phi }$ such that

$$d(Tx,Ty)\le \phi (d(gx,gy))\mathit{\text{for all }}x,y\in X\mathit{\text{ such that }}gx\preccurlyeq gy.$$

(19)

Also suppose that

$$\phi (0)=0\mathit{\text{or}}\preccurlyeq \mathit{\text{ is antisymmetric.}}$$

Assume that either

• (a) T and g are continuous and commuting, or

• (b) $(X,d,\preccurlyeq )$ is regular and gX is closed.

If there exists a point $x_0\in X$ such that $g{x}_0\preccurlyeq T{x}_0$, then T and g have, at least, a coincidence point.

4 Applications to G-metric spaces

One of the most interesting, recent lines of research in the field of fixed point theory is devoted to G-metric spaces. Taking into account Lemma 2.2, we can take advantage of our main results to present some new theorems in this area. The following result is an easy application to G-metric spaces.

Corollary 4.1 Let $(X,G)$ be a complete G-metric space, let $T,g:X\to X$ be two mappings such that $T(X)\subseteq g(X)$, and let $\mathcal{M}\subseteq X^2$ be a g-transitive, $(T,g)$-closed, nonempty subset of  $X^2$. Assume that T and g are continuous and commuting, and there exists $\phi \in \mathrm{\Phi }$ such that

$$G(Tx,Tx,Ty)\le \phi (G(gx,gx,gy))$$

for all $x,y\in X$ such that $(gx,gy)\in \mathcal{M}$. If there exists $x_0\in X$ such that $(g{x}_0,T{x}_0)\in \mathcal{M}$, then T and g have, at least, a coincidence point.

Notice that this result is also valid if $\phi \in \mathrm{\Psi }$ and ℳ is $(T,g)$-compatible.

Proof It follows from Theorem 3.3 and Corollary 3.1 using the quasi-metric $q_G^{\prime }$ associated to G (as in Lemma 2.2). Notice that there exists a $(T,g,\mathcal{M})$-Picard sequence on X by items 1 and 2 of Lemma 3.2. □

In order not to lose the power and usability of Theorems 3.3 and 3.4, we present the following properties comparing $q_G$ and $q_G^{\prime }$.

Definition 4.1 Let $(X,G)$ be a G-metric space, and let $A\subseteq X$ and $\mathcal{M}\subseteq X^2$ be two nonempty subsets. We say that $(A,G,\mathcal{M})$ is regular (or A is $(G,\mathcal{M})$ -regular) if we have that $(x_n,u)\in \mathcal{M}$ for all n provided that $\{x_n\}$ is a G-convergent sequence on A, $u\in A$ is its G-limit and $(x_n,x_m)\in \mathcal{M}$ for all $n<m$.

Lemma 4.1 Given a G-metric space $(X,G)$ and nonempty subsets $\mathcal{M}\subseteq X^2$ and $A\subseteq X$, the following conditions are equivalent:

• 1. the subset A is $(G,\mathcal{M})$-regular;

• 2. the subset A is $(q_G,\mathcal{M})$-regular;

• 3. the subset A is $(q_G^{\prime },\mathcal{M})$-regular.

Proof It follows from the fact that $(X,G)$, $(X,q_G)$ and $(X,q_G^{\prime })$ have the same convergent sequences, and they converge to the same limits. □

Similarly, the following result can be proved.

Lemma 4.2 Given a G-metric space $(X,G)$, a nonempty subset $\mathcal{M}\subseteq X^2$ and two mappings $T,g:X\to X$, we have that the pair $(T,g)$ is $(O,\mathcal{M})$-compatible (respectively, $(O^{\prime },\mathcal{M})$-compatible) in $(X,q_G)$ if and only if it is $(O,\mathcal{M})$-compatible (respectively, $(O^{\prime },\mathcal{M})$-compatible) in $(X,q_G^{\prime })$.

Proof It follows from the fact that $(X,q_G)$ and $(X,q_G^{\prime })$ have the same convergent sequences, and they converge to the same limits. Furthermore, taking into account that $q_G\le 2q_G^{\prime }\le 4q_G$, then $\{q_G(x_n,y_n)\}\to 0$ if and only if $\{q_G^{\prime }(x_n,y_n)\}\to 0$. □

Definition 4.2 Let $(X,G)$ be a G-metric space, and let ℳ be a nonempty subset of $X^2$. Two mappings $T,g:X\to X$ are said to be $(O,\mathcal{M})$ -compatible if the pair $(T,g)$ is $(O,\mathcal{M})$-compatible in $(X,q_G)$ (or, equivalently, in $(X,q_G^{\prime })$).

Similarly, the notion of $(O^{\prime },\mathcal{M})$-compatibility in a G -metric space $(X,G)$ can be defined. We present the following result, which is a complete version of our main results in the context of G-metric spaces.

Corollary 4.2 Let $(X,G)$ be a G-metric space, let $T,g:X\to X$ be two mappings, and let ℳ be a nonempty subset of $X^2$. Suppose that, at least, one of the following conditions holds.

• (A) There exists a $(T,g,\mathcal{M})$-Picard sequence on X.

(${\mathrm{A}}^{\prime }$) $T(X)\subseteq g(X)$ and ℳ is g-transitive and $(T,g)$-closed.

(${\mathrm{A}}^{″}$) ℳ is g-transitive and $(T,g)$-closed, and there exists a $(T,g)$-Picard sequence ${\{x_n\}}_{n\ge 0}$ such that $(g{x}_0,T{x}_0)\in \mathcal{M}$.

Also assume that, at least, one of the following two conditions holds.

(B) There exists $\phi \in \mathrm{\Phi }$ such that

$$G(Tx,Tx,Ty)\le \phi (G(gx,gx,gy))$$

for all $x,y\in X$ for which $(gx,gy)\in \mathcal{M}$.

(B′) The subset ℳ is $(T,g)$-compatible and there exists $\phi \in \mathrm{\Psi }$ such that

$$G(Tx,Tx,Ty)\le \phi (G(gx,gx,gy))$$

for all $x,y\in X$ for which $(gx,gy)\in \mathcal{M}$.

Additionally, assume that, at least, one of the following eight conditions holds.

• (a) X (or $g(X)$ or $T(X)$) is G-complete, T and g are ℳ-continuous and the pair $(T,g)$ is $(O^{\prime },\mathcal{M})$-compatible;

  (a′) X (or $g(X)$ or $T(X)$) is G-complete, T and g are continuous and the pair $(T,g)$ is $(O^{\prime },\mathcal{M})$-compatible;

• (b) X (or $g(X)$ or $T(X)$) is G-complete and T and g are ℳ-continuous and commuting;

(b′) X (or $g(X)$ or $T(X)$) is G-complete and T and g are continuous and commuting;

• (c) $(g(X),G)$ is complete and X (or $g(X)$) is $(G,\mathcal{M})$-regular;

• (d) $(X,G)$ is complete, $g(X)$ is closed and X (or $g(X)$) is $(G,\mathcal{M})$-regular;

• (e) $(X,G)$ is complete, g is ℳ-continuous, ℳ is g-closed, the pair $(T,g)$ is $(O,\mathcal{M})$-compatible and X is $(G,\mathcal{M})$-regular.

  (e′) $(X,G)$ is complete, g is continuous, ℳ is g-closed, the pair $(T,g)$ is $(O,\mathcal{M})$-compatible and X is $(G,\mathcal{M})$-regular.

Then T and g have, at least, a coincidence point.

Proof It follows from Theorems 3.3 and 3.4 taking into account Corollary 3.1, Lemmas 2.2, 4.2 and Definition 4.2. Notice that (A′) ⇒ (${\mathrm{A}}^{″}$) ⇒ (A), (a′) ⇒ (a), (b′) ⇒ (b) and (e′) ⇒ (e). □

We particularize the previous result to the case in which $\mathcal{M}={\mathcal{M}}_{\preccurlyeq }$, associated to a preorder or a partial order ≼ on X. In such a case, Lemma 3.1 is applicable. We leave to the reader to interpret ≼-nondecreasing-continuity as ${\mathcal{M}}_{\preccurlyeq }$-continuity, G-regularity as $(G,{\mathcal{M}}_{\preccurlyeq })$-compatibility, O-compatibility as $(O,{\mathcal{M}}_{\preccurlyeq })$-compatibility, and $O^{\prime }$-compatibility as $(O^{\prime },{\mathcal{M}}_{\preccurlyeq })$-compatibility.

Corollary 4.3 Let $(X,G)$ be a G-metric space provided with a preorder ≼, and let $T,g:X\to X$ be two mappings such that $T(X)\subseteq g(X)$ and T is $(g,\preccurlyeq )$-nondecreasing. Assume that, at least, one of the following two conditions holds.

(B) There exists $\phi \in \mathrm{\Phi }$ such that

$$G(Tx,Tx,Ty)\le \phi (G(gx,gx,gy))$$

for all $x,y\in X$ for which $gx\preccurlyeq gy$.

(B′) ≼ is a partial order on X and there exists $\phi \in \mathrm{\Psi }$ such that

$$G(Tx,Tx,Ty)\le \phi (G(gx,gx,gy))$$

for all $x,y\in X$ for which $gx\preccurlyeq gy$.

Additionally, assume that, at least, one of the following eight conditions holds.

• (a) X (or $g(X)$ or $T(X)$) is G-complete, T and g are ≼-nondecreasing-continuous and the pair $(T,g)$ is $O^{\prime }$-compatible;

  (a′) X (or $g(X)$ or $T(X)$) is G-complete, T and g are continuous and the pair $(T,g)$ is $O^{\prime }$-compatible;

• (b) X (or $g(X)$ or $T(X)$) is G-complete and T and g are ≼–nondecreasing-continuous and commuting;

(b′) X (or $g(X)$ or $T(X)$) is G-complete and T and g are continuous and commuting;

• (c) $(g(X),G)$ is complete and X (or $g(X)$) is G-regular;

• (d) $(X,G)$ is complete, $g(X)$ is closed and X (or $g(X)$) is G-regular;

• (e) $(X,G)$ is complete, g is ≼-nondecreasing and ≼-nondecreasing-continuous, the pair $(T,g)$ is O-compatible and X is G-regular.

(e′) $(X,G)$ is complete, g is ≼-nondecreasing and continuous, the pair $(T,g)$ is O-compatible and X is G-regular.

If there exists $x_0\in X$ verifying $g{x}_0\preccurlyeq T{x}_0$, then T and g have, at least, a coincidence point.

We also leave to the reader the task of particularizing the previous results to the case in which g is the identity mapping on X, obtaining fixed points of T.

5 Coupled coincidence point theorems

In this section, we deduce that Theorem 1.1 follows from Theorem 3.3. However, the main aim of this subsection is to describe how Theorems 3.1, 3.2, 3.3 and 3.4 can be employed in order to obtain some coupled coincidence point theorems, because these techniques can be extrapolated to many contexts.

We introduce the following notation. Given two mappings $F:X^2\to X$ and $g:X\to X$, we define $T_F,\mathcal{G}:X^2\to X^2$, for all $(x,y)\in X^2$, by

$$T_F(x,y)=(F(x,y),F(y,x))\text{and}\mathcal{G}(x,y)=(gx,gy).$$

Lemma 5.1 Let $F:X^2\to X$ and $g:X\to X$ be two mappings.

• 1. If $F(X^2)\subseteq g(X)$, then $T_F(X^2)\subseteq \mathcal{G}(X^2)$.

• 2. If F and g are commuting, then $T_F$ a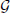nd are also commuting.

• 3. A point $(x,y)\in X^2$ is a coincidence point of $T_F$ a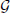nd if and only if it is a coincidence point of F and g.

Proof (2) It follows from

$$\begin{array}{rl}{T}_F\mathcal{G}(x,y)& =T_F(gx,gy)=(F(gx,gy),F(gy,gx))=(gF(x,y),gF(y,x))\\ =\mathcal{G}(F(x,y),F(y,x))=\mathcal{G}{T}_F(x,y)\end{array}$$

for all $(x,y)\in X^2$. □

5.1 Charoensawan and Thangthong’s coupled coincidence point result in G-metric spaces

One of the key objectives of this subsection is to prove that, in Theorem 1.1, the middle variables of M are not necessary. Indeed, given a nonempty subset $M\subseteq X^6$, let us define

$$M^{\prime }=\{(x,u,y,v)\in X^4:(y,v,y,v,x,u)\in M\}.$$

(20)

Notice that $M^{\prime }$ is a subset of $X^4=X^2\times X^2$.

Lemma 5.2 Let $F:X^2\to X$ and $g:X\to X$ be two mappings, and let $M\subseteq X^6$.

• 1. If there exist $x_0,y_0\in X$ such that

  $$(F(x_0,y_0),F(y_0,x_0),F(x_0,y_0),F(y_0,x_0),g{x}_0,g{y}_0)\in M,$$

then $(\mathcal{G}(x_0,y_0),T_F(x_0,y_0))\in M^{\prime }$. In particular, $M^{\prime }$ is nonempty.

• 2. If M is transitive, then $M^{\prime }$ is transitive and 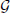-transitive.

• 3. If M verifies the second property of Definition  1.1, then $M^{\prime }$ is a $(T_F,\mathcal{G})$-closed set.

• 4. If M is an $(F^{\ast },g)$-invariant set, then $M^{\prime }$ is a $(T_F,\mathcal{G})$-closed set.

We point out that we will only use the second property of the notion of $(F^{\ast },g)$-invariant set (Definition 1.1). This shows that $(T,g)$-closed sets are more general than an $(F^{\ast },g)$-invariant set because the first property will not be employed (this was also established in Kutbi et al. [5]).

Proof (1) By definition, $(F(x_0,y_0),F(y_0,x_0),F(x_0,y_0),F(y_0,x_0),g{x}_0,g{y}_0)\in M$ implies that $(g{x}_0,g{y}_0,F(x_0,y_0),F(y_0,x_0))\in M^{\prime }$, which means that $(\mathcal{G}(x_0,y_0),T_F(x_0,y_0))\in M^{\prime }$.

(2) Assume that M is transitive, and let $x,u,y,v,z,w\in X$ be such that $(x,u,y,v),(y,v,z,w)\in M^{\prime }$. Therefore

$$(z,w,z,w,y,v),(y,v,y,v,x,u)\in M.$$

As M is transitive, then $(z,w,z,w,x,u)\in M$, so $(x,u,z,w)\in M^{\prime }$. Therefore, $M^{\prime }$ is transitive, and it is also 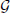-transitive because every transitive subset is also 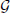-transitive, whatever .

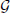• (3) Assume that M is an $(F^{\ast },g)$-invariant set, and let $x,u,y,v\in X$ be such that $(\mathcal{G}(x,u),\mathcal{G}(y,v))\in M^{\prime }$. By definition, since $(gx,gu,gy,gv)\in M^{\prime }$, then $(gy,gv,gy,gv,gx,gu)\in M$. As M is $(F^{\ast },g)$-invariant, then

  $$(F(y,v),F(v,y),F(y,v),F(v,y),F(x,u),F(u,x))\in M.$$

In particular, $(F(x,u),F(u,x),F(y,v),F(v,y))\in M^{\prime }$, which means that $(T_F(x,u),T_F(y,v))\in M^{\prime }$. Hence, $M^{\prime }$ is a $(T_F,\mathcal{G})$-closed set. □

In the following result, we use the quasi-metric $q_{G_2}$ on $X^2$ associated, by Lemma 2.2, to the G-metric $G_2:X^2\times X^2\times X^2\to [0,\mathrm{\infty })$ given by

$$G_2((x,u),(y,v),(z,w))=G(x,y,z)+G(u,v,w),$$

that is, for all $(x,u),(y,v)\in X^2$,

$$q_{G_2}((x,u),(y,v))=G_2((x,u),(y,v),(y,v))=G(x,y,y)+G(u,v,v).$$

Using this notation, the following result is obvious.

Lemma 5.3 Let $(X,G)$ be a G-metric space, and let M be a nonempty subset of $X^6$ such that $M^{\prime }$ is nonempty. Let $F:X^2\to X$ and $g:X\to X$ be two mappings such that there exists $\phi \in \mathrm{\Phi }$ verifying

$$\begin{array}{r}[G(F(x,u),F(y,v),F(y,v))+G(F(u,x),F(v,y),F(v,y))]\\ \le \varphi (G(gx,gy,gy)+G(gu,gv,gv))\end{array}$$

(21)

for all $(gy,gv,gy,gv,gx,gu)\in M$. Then

$$q_{G_2}(T_F(x,u),T_F(y,v))\le \phi \left(q_{G_2}(\mathcal{G}(x,u),\mathcal{G}(y,v))\right)$$

for all $(x,u),(y,v)\in X^2$ such that $(\mathcal{G}(x,u),\mathcal{G}(y,v))\in M^{\prime }$.

Notice that condition (21) is weaker than condition (1). The previous properties prove the following consequence.

Lemma 5.4 Let $(X,G)$ be a G-metric space, and let $F:X^2\to X$ and $g:X\to X$ be two mappings.

• 1. If F is G-continuous, then $T_F$ is $q_{G_2}$-continuous.

• 2. If g is G-continuous, then 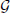is $q_{G_2}$-continuous.

Proof It is a straightforward exercise. □

Corollary 5.1 Theorem  1.1 follows from Theorem  3.3.

Proof Under the hypothesis of Theorem 1.1, let us consider the quasi-metric space $(X^2,q_{G_2})$, the mappings $T_F$ a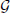nd and the subset $M^{\prime }$ defined by (20). By item 3 of Lemma 2.1, $(X^2,G_2)$ is a complete G-metric space, and by item 7 of Lemma 2.2, $(X^2,q_{G_2})$ is a complete quasi-metric space. Furthermore, Corollary 3.1 guarantees that $(X^2,q_{G_2})$ is left/right-Cauchy and left/right-convergent. Lemma 5.4 ensures that 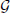$T_F$ and are $q_{G_2}$-continuous. Lemma 5.2 proves that $T_F(X^2)\subseteq \mathcal{G}(X^2)$ and $M^{\prime }$ is a transitive, $(T_F,\mathcal{G})$-closed, nonempty subset of ${(X^2)}^2$. Finally, Lemma 5.3 ensures that $T_F$ is a $(\mathcal{G},M^{\prime },\mathrm{\Phi })$-contraction of the second kind. As a consequence, case (b) of Theorem 3.3 (replacing condition (A) by (A′), and ℳ-continuity by continuity) guarantees that $T_F$ a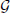nd have, at least, a coincidence point, which is a coincidence point of F and g. □

In fact, the previous proof shows that two conditions are not necessary in Theorem 3.3: neither the first property of $(F^{\ast },g)$-invariant sets nor the middle variables of M in $X^6$.

5.2 Kutbi et al.’s coupled fixed point theorems without the mixed monotone property

In [5], the authors introduced the following notion and proved the following result.

Definition 5.1 (Kutbi et al. [5])

Let $F:X^2\to X$ be a mapping, and let M be a nonempty subset of $X^4$. We say that M is an F-closed subset of $X^4$ if, for all $x,y,u,v\in X$,

$$(x,y,u,v)\in M⟹(F(x,y),F(y,x),F(u,v),F(v,u))\in M.$$

Corollary 5.2 (Kutbi et al. [5], Theorem 16)

Let $(X,d)$ be a complete metric space, let $F:X\times X\to X$ be a continuous mapping, and let M be a subset of $X^4$. Assume that:

• (i) M is F-closed;

• (ii) there exists $(x_0,y_0)\in X^2$ such that $(F(x_0,y_0),F(y_0,x_0),x_0,y_0)\in M$;

• (iii) there exists $k\in [0,1)$ such that for all $(x,y,u,v)\in M$, we have

  $$d(F(x,y),F(u,v))+d(F(y,x),F(v,u))\le k(d(x,u)+d(y,v)).$$

Then F has a coupled fixed point.

5.3 Sintunaravat et al.’s coupled fixed point theorems without the mixed monotone property

Similarly, the following result is a consequence of our main results.

Corollary 5.3 (Sintunaravat et al. [21])

Let $(X,d)$ be a complete metric space and M be a nonempty subset of $X^4$. Assume that there is a function $\phi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ with $0=\phi (0)<\phi (t)<t$ and ${lim}_{r\to t^{+}}\phi (r)<t$ for each $t>0$, and also suppose that $F:X\times X\to X$ is a mapping such that

$$d(F(x,y),F(u,v))\le \phi \left(\frac{d(x,u)+d(y,v)}{2}\right)$$

(22)

for all $(x,y,u,v)\in M$. Suppose that either

• (a) F is continuous, or

• (b) for any two sequences $\{x_m\}$, $\{y_m\}$ with $(x_{m+1},y_{m+1},x_m,y_m)\in M$,

  $$\{x_m\}\to x,\{y_m\}\to y,$$

for all $m\ge 1$, then $(x,y,x_m,y_m)\in M$ for all $m\ge 1$.

If there exists $(x_0,y_0)\in X\times X$ such that $(F(x_0,y_0),F(y_0,x_0),x_0,y_0)\in M$ and M is an F-invariant set which satisfies the transitive property, then there exist $x,y\in X$ such that $x=F(x,y)$ and $y=F(y,x)$, that is, F has a coupled fixed point.

5.4 Choudhury and Kundu’s coupled coincidence point theorems under the mixed g-monotone property

Although our main results in Section 3 do not need the mixed monotone property, we show in this subsection how to interpret that property using a subset $M\subseteq X^4$, so that our main results are also applicable to this context. We start recalling this notion.

Definition 5.2 Let ≼ be a binary relation on X, and let $F:X^2\to X$ and $g:X\to X$ be two mappings. We say that F has the mixed g-monotone property (with respect to ≼) if $F(x,y)$ is monotone g-nondecreasing in x and monotone g-nonincreasing in y, that is, for any $x,y\in X$ ,

$$\begin{array}{r}{x}_1,x_2\in X,g{x}_1\preccurlyeq g{x}_2\Rightarrow F(x_1,y)\preccurlyeq F(x_2,y)\text{and}\\ y_1,y_2\in X,g{y}_1\preccurlyeq g{y}_2\Rightarrow F(x,y_1)\succcurlyeq F(x,y_2).\end{array}$$

The binary relation ≼ on X can be extended to $X^2$ as follows:

$$(x,y),(u,v)\in X^2,(x,y)⊑(u,v)\iff [x\preccurlyeq u,y\succcurlyeq v].$$

If ≼ is a partial order on X, then ⊑ is a partial order on $X^2$. It is easy to show that if F has the mixed $(g,\preccurlyeq )$-monotone property, then $T_F$ is a $(\mathcal{G},⊑)$-nondecreasing mapping and, by Lemma, ${\mathcal{M}}_{⊑}\subseteq X^4$ is $(T_F,\mathcal{G})$-closed.

Corollary 5.4 (Choudhury and Kundu [17], Theorem 3.1)

Let $(X,\preccurlyeq )$ be a partially ordered set, and let there be a metric d on X such that $(X,d)$ is a complete metric space. Let $\phi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ be such that $\phi (t)<t$ and ${lim}_{r\to t^{+}}\phi (r)<t$ for all $t>0$. Let $F:X\times X\to X$ and $g:X\to X$ be two mappings such that F has the mixed g-monotone property and satisfy

$$\begin{array}{r}d(F(x,y),F(u,v))\le \phi \left(\frac{d(gx,gu)+d(gy,gv)}{2}\right)\\ \mathit{\text{for all }}x,y,u,v\in X\mathit{\text{ with }}gx\preccurlyeq gu\mathit{\text{ and }}gy\succcurlyeq gv.\end{array}$$

Let $F(X\times X)\subseteq g(X)$, g be continuous and monotone increasing and F and g be compatible mappings. Also suppose that

• (a) F is continuous, or

• (b) X has the following properties:

• (i) if a nondecreasing sequence $\{x_n\}\to x$, then $x_n\preccurlyeq x$ for all $n\ge 0$;

• (ii) if a nonincreasing sequence $\{y_n\}\to y$, then $y_n\succcurlyeq y$ for all $n\ge 0$.

If there exist $x_0,y_0\in X$ such that $g{x}_0\preccurlyeq F(x_0,y_0)$ and $g{y}_0\succcurlyeq F(y_0,x_0)$, then there exist $x,y\in X$ such that $gx=F(x,y)$ and $gy=F(y,x)$, that is, F and g have a coupled coincidence point in X.

Proof It is only necessary to consider the metric $D^2$ on $X^2$ given by

$$D^2((x,y),(u,v))=\frac{d(x,u)+d(y,v)}{2}\text{for all }(x,y),(u,v)\in X^2$$

and to use the previous properties in $(X^2,D^2,⊑)$ usin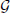g $T_F$ and . □

6 Conclusions

As conclusion, we highlight that coupled coincidence point theorems can be easily deduced from Theorems 3.1, 3.2, 3.3 and 3.4 applied to the quintuple $(X^2,q_{G_2},T_F,\mathcal{G},M^{\prime })$. Exactly in the same way, tripled, quadrupled and multidimensional coincidence point results can be derived (following the arguments in [9, 20, 22–26]).