- Research Article
- Open access
- Published:
Fixed Point Theorems in Cone Banach Spaces
Fixed Point Theory and Applications volume 2009, Article number: 609281 (2009)
Abstract
In this manuscript, a class of self-mappings on cone Banach spaces which have at least one fixed point is considered. More precisely, for a closed and convex subset  of a cone Banach space with the norm
of a cone Banach space with the norm  , if there exist
, if there exist  ,
,  ,
,  and
and  satisfies the conditions
satisfies the conditions  and
and  for all
for all  , then
, then  has at least one Fixed point.
has at least one Fixed point.
1. Introduction and Preliminaries
In 1980, Rzepecki [1] introduced a generalized metric  on a set
on a set  in a way that
in a way that  , where
, where  is Banach space and
is Banach space and  is a normal cone in
is a normal cone in  with partial order
with partial order  . In that paper, the author generalized the fixed point theorems of Maia type [2].
. In that paper, the author generalized the fixed point theorems of Maia type [2].
Let
 be a nonempty set endowed in two metrics
be a nonempty set endowed in two metrics
 ,
,
 and
and
 a mapping of
a mapping of
 into itself. Suppose that
into itself. Suppose that
 for all
for all
 , and
, and
 is complete space with respect to
is complete space with respect to
 , and
, and
 is continuous with respect to
is continuous with respect to
 , and
, and
 is contraction with respect to
is contraction with respect to
 , that is,
, that is,
 for all
for all
 , where
, where
 . Then
. Then
 has a unique fixed point in
has a unique fixed point in
 .
.
Seven years later, Lin [3] considered the notion of  -metric spaces by replacing real numbers with cone
-metric spaces by replacing real numbers with cone  in the metric function, that is,
in the metric function, that is,  . In that manuscript, some results of Khan and Imdad [4] on fixed point theorems were considered for
. In that manuscript, some results of Khan and Imdad [4] on fixed point theorems were considered for  -metric spaces. Without mentioning the papers of Lin and Rzepecki, in 2007, Huang and Zhang [5] announced the notion of cone metric spaces (CMS) by replacing real numbers with an ordering Banach space. In that paper, they also discussed some properties of convergence of sequences and proved the fixed point theorems of contractive mapping for cone metric spaces: any mapping
-metric spaces. Without mentioning the papers of Lin and Rzepecki, in 2007, Huang and Zhang [5] announced the notion of cone metric spaces (CMS) by replacing real numbers with an ordering Banach space. In that paper, they also discussed some properties of convergence of sequences and proved the fixed point theorems of contractive mapping for cone metric spaces: any mapping  of a complete cone metric space
of a complete cone metric space  into itself that satisfies, for some
into itself that satisfies, for some  , the inequality
, the inequality

for all  , has a unique fixed point.
, has a unique fixed point.
Recently, many results on fixed point theorems have been extended to cone metric spaces (see, e.g., [5–9]). Notice also that in ordered abstract spaces, existence of some fixed point theorems is presented and applied the resolution of matrix equations (see, e.g., [10–12]).
In this manuscript, some of known results (see, e.g., [13, 14]) are extended to cone Banach spaces which were defined and used in [15, 16] where the existence of fixed points for self-mappings on cone Banach spaces is investigated.
Throughout this paper  stands for real Banach space. Let
stands for real Banach space. Let  always be a closed nonempty subset of
always be a closed nonempty subset of  .
.  is called cone if
is called cone if  for all
for all  and nonnegative real numbers
and nonnegative real numbers  where
where  and
and  .
.
For a given cone  , one can define a partial ordering (denoted by
, one can define a partial ordering (denoted by  or
or  ) with respect to
) with respect to  by
by  if and only if
if and only if  . The notation
. The notation  indicates that
indicates that  and
and  , while
, while  will show
will show  , where
, where  denotes the interior of
denotes the interior of  . From now on, it is assumed that
. From now on, it is assumed that 
The cone  is called
is called
normal if there is a number  such that for all
such that for all  :
:

regular if every increasing sequence which is bounded from above is convergent. That is, if  is a sequence such that
is a sequence such that  for some
for some  , then there is
, then there is  such that
such that  .
.
In  , the least positive integer
, the least positive integer  , satisfying (1.2), is called the normal constant of
, satisfying (1.2), is called the normal constant of  .
.
-
(i)
Every regular cone is normal.
(ii)For each  , there is a normal cone with normal constant
, there is a normal cone with normal constant  .
.
-
(iii)
The cone
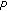 is regular if every decreasing sequence which is bounded from below is convergent.
is regular if every decreasing sequence which is bounded from below is convergent.
Proofs of (i) and (ii) are given in [6] and the last one follows from definition.
Definition 1.2 (see [5]).
Let  be a nonempty set. Suppose the mapping
be a nonempty set. Suppose the mapping  satisfies
satisfies
 for all
for all  ,
,
 if and only if
if and only if  ,
,
 for all
for all  ,
,
 for all
for all  ,
,
then  is called cone metric on
is called cone metric on  , and the pair
, and the pair  is called a cone metric space (CMS).
is called a cone metric space (CMS).
Example 1.3.
Let  ,
,  , and
, and  . Define
. Define  by
by  , where
, where  are positive constants. Then
are positive constants. Then  is a CMS. Note that the cone
is a CMS. Note that the cone  is normal with the normal constant
is normal with the normal constant 
It is quite natural to consider Cone Normed Spaces (CNS).
Definition 1.4 (see [15, 16]).
Let  be a vector space over
be a vector space over  . Suppose the mapping
. Suppose the mapping  satisfies
satisfies
 for all
for all  ,
,
 if and only if
if and only if  ,
,
 for all
for all  ,
,
 for all
for all  ,
,
then  is called cone norm on
is called cone norm on  , and the pair
, and the pair  is called a cone normed space (CNS).
is called a cone normed space (CNS).
Note that each CNS is CMS. Indeed,  .
.
Definition 1.5.
Let  be a CNS,
be a CNS,  and
and  a sequence in
a sequence in  . Then
. Then
(i) converges to
converges to whenever for every
whenever for every  with
with  there is a natural number
there is a natural number  , such that
, such that  for all
for all  . It is denoted by
. It is denoted by  or
or  ;
;
(ii) is a Cauchy sequence whenever for every
is a Cauchy sequence whenever for every  with
with  there is a natural number
there is a natural number  , such that
, such that  for all
for all  ;
;
(iii) is a complete cone normed space if every Cauchy sequence is convergent.
is a complete cone normed space if every Cauchy sequence is convergent.
Complete cone normed spaces will be called cone Banach spaces.
Lemma 1.6.
Let  be a CNS,
be a CNS,  a normal cone with normal constant
a normal cone with normal constant  , and
, and  a sequence in
a sequence in  . Then,
. Then,
(i)the sequence  converges to
converges to  if and only if
if and only if  , as
, as  ;
;
(ii)the sequence  is Cauchy if and only if
is Cauchy if and only if  as
as  ;
;
(iii)the sequence  converges to
converges to  and the sequence
and the sequence  converges to
converges to  then
then  .
.
The proof is direct by applying [5, Lemmas  ,
,  , and
, and  ] to the cone metric space
] to the cone metric space  , where
, where  , for all
, for all  .
.
Let  be a CNS over a cone
be a CNS over a cone  in
in  . Then
. Then 
 and
and  ,
,  .
.  If
If  then there exists
then there exists  such that
such that  implies
implies  .
.  For any given
For any given  and
and  , there exists
, there exists  such that
such that  .
.  If
If  are sequences in
are sequences in  such that
such that  ,
,  , and
, and  , for all
, for all  then
then  .
.
The proofs of the first two parts followed from the definition of  . The third part is obtained by the second part. Namely, if
. The third part is obtained by the second part. Namely, if  is given then find
is given then find  such that
such that  implies
implies  . Then find
. Then find  such that
such that  and hence
and hence  . Since
. Since  is closed, the proof of fourth part is achieved.
is closed, the proof of fourth part is achieved.
Definition 1.8 (see [17]).
 is called minihedral cone if
is called minihedral cone if  exists for all
exists for all  , and strongly minihedral if every subset of
, and strongly minihedral if every subset of  which is bounded from above has a supremum.
which is bounded from above has a supremum.
Lemma 1.9 (see [18]).
Every strongly minihedral normal cone is regular.
Example 1.10.
Let  with the supremum norm and
with the supremum norm and  Then
Then  is a cone with normal constant
is a cone with normal constant  which is not regular. This is clear, since the sequence
which is not regular. This is clear, since the sequence  is monotonically decreasing, but not uniformly convergent to
is monotonically decreasing, but not uniformly convergent to  . This cone, by Lemma 1.9, is not strongly minihedral. However, it is easy to see that the cone mentioned in Example 1.3 is strongly minihedral.
. This cone, by Lemma 1.9, is not strongly minihedral. However, it is easy to see that the cone mentioned in Example 1.3 is strongly minihedral.
Definition 1.11.
Let  be a closed and convex subset of a cone Banach space with the norm
be a closed and convex subset of a cone Banach space with the norm  and
and  a mapping which satisfies the condition
a mapping which satisfies the condition

for all  . Then,
. Then,  is said to satisfy the condition
is said to satisfy the condition  .
.
For  , the set of fixed points of
, the set of fixed points of  is denoted by
is denoted by  .
.
Definition 1.12 (see [14]).
Let  be a closed and convex subset of a cone Banach space with the norm
be a closed and convex subset of a cone Banach space with the norm  and
and  a mapping. Consider the conditions
a mapping. Consider the conditions


Then  is called nonexpansive (resp., quasi-nonexpansive) if it satisfies the condition (1.4) (resp., (1.5)).
is called nonexpansive (resp., quasi-nonexpansive) if it satisfies the condition (1.4) (resp., (1.5)).
2. Main Results
From now on,  will be a cone Banach space,
will be a cone Banach space,  a normal cone with normal constant
a normal cone with normal constant  and
and  a self-mapping operator defined on a subset
a self-mapping operator defined on a subset  of
of  .
.
Theorem 2.1.
Let  with
with  and let
and let  be a complete cone metric space
be a complete cone metric space  an onto mapping which satisfies the condition
an onto mapping which satisfies the condition

Then,  has a unique fixed point.
has a unique fixed point.
Proof.
Let  and
and  , then by (2.1), one can observe
, then by (2.1), one can observe  which is a contradiction. Thus,
which is a contradiction. Thus,  is one-to-one and it has an inverse, say
is one-to-one and it has an inverse, say  . Hence,
. Hence,

By [5, Theorem  ],
],  has a unique fixed point which is equivalent to saying that
has a unique fixed point which is equivalent to saying that  has a unique fixed point.
has a unique fixed point.
The following statement is consequence of Definition 1.11.
Proposition 2.2.
Every nonexpansive mapping satisfies the condition  .
.
Proposition 2.3.
Let  satisfy the condition
satisfy the condition  and
and  , then
, then  is a quasi-nonexpansive.
is a quasi-nonexpansive.
Proof.
Let  and
and  . Since
. Since  and satisfies the condition
and satisfies the condition  ,
,

Theorem 2.4.
Let  be a closed and convex subset of a cone Banach space
be a closed and convex subset of a cone Banach space  with the norm
with the norm  and
and  a mapping which satisfies the condition
a mapping which satisfies the condition

for all  , where
, where  . Then,
. Then,  has at least one fixed point.
has at least one fixed point.
Proof.
Let  be arbitrary. Define a sequence
be arbitrary. Define a sequence  in the following way:
in the following way:

Notice that

which yields that

for  Combining this observation with the condition (2.4), one can obtain
Combining this observation with the condition (2.4), one can obtain

Thus,  , where
, where  . Hence,
. Hence,  is a Cauchy sequence in
is a Cauchy sequence in  and thus converges to some
and thus converges to some  Regarding the inequality
Regarding the inequality

and by the help of Lemma 1.6(iii), one can obtain

Taking into account (2.6) and (2.4), substituting  and
and  implies that
implies that

Thus, when  , one can get
, one can get  , that is,
, that is,  .
.
Notice that identity map,  , satisfies the condition (2.4). Thus, maps that satisfy the condition (2.4) may have fixed points.
, satisfies the condition (2.4). Thus, maps that satisfy the condition (2.4) may have fixed points.
From the triangle inequality,

By (2.4),

Thus, letting  implies that
implies that

Hence we have the following conclusion.
Theorem 2.5.
Let  be a closed and convex subset of a cone Banach space with the norm
be a closed and convex subset of a cone Banach space with the norm  and
and  a mapping which satisfies the condition
a mapping which satisfies the condition

for all  , where
, where  . Then
. Then  has a fixed point.
has a fixed point.
Theorem 2.6.
Let  be a closed and convex subset of a cone Banach space with the norm
be a closed and convex subset of a cone Banach space with the norm  and
and  a mapping which satisfies the condition
a mapping which satisfies the condition

for all  , where
, where  . Then
. Then  has at least one fixed point.
has at least one fixed point.
Proof.
Construct a sequence  as in the proof of Theorem 2.4, that is, (2.5), (2.6) and also
as in the proof of Theorem 2.4, that is, (2.5), (2.6) and also

hold. Thus the triangle inequality implies

Then, by (2.17) and (2.7) we obtain

Replacing  and
and  in (2.16) and regarding (2.7) and (2.19), one can obtain
in (2.16) and regarding (2.7) and (2.19), one can obtain

and thus,  . Since
. Since  , the sequence
, the sequence  is a Cauchy sequence that converges to some
is a Cauchy sequence that converges to some  . Since
. Since  also converges to
also converges to  as in the proof of Theorem 2.4, the inequality (2.16) (under the assumption
as in the proof of Theorem 2.4, the inequality (2.16) (under the assumption  and
and  ) by the help of Lemma 1.6(iii) yields that
) by the help of Lemma 1.6(iii) yields that  which is equivalent to saying that
which is equivalent to saying that 
Theorem 2.7.
Let  be a closed and convex subset of a cone Banach space with the norm
be a closed and convex subset of a cone Banach space with the norm  . If there exist
. If there exist  and
and  satisfies the conditions
satisfies the conditions


for all  . Then,
. Then,  has at least one fixed point.
has at least one fixed point.
Proof.
Construct a sequence  as in the proof of Theorem 2.4. We claim that the inequality (2.22) for
as in the proof of Theorem 2.4. We claim that the inequality (2.22) for  and
and  implies that
implies that

for all  that satisfy (2.21). For the proof of the claim, first recall from (2.7) that
that satisfy (2.21). For the proof of the claim, first recall from (2.7) that

The case  is trivially true. Indeed, taking into account (2.22) with
is trivially true. Indeed, taking into account (2.22) with  and
and  together with (2.24) and (2.19), one can get
together with (2.24) and (2.19), one can get

which is equivalent to (2.23) since  . For the case
. For the case  , consider the inequality
, consider the inequality  which is equivalent to
which is equivalent to

By substituting  and
and  in (2.22) together with (2.24), (2.26) and (2.17), one can get
in (2.22) together with (2.24), (2.26) and (2.17), one can get

which is equivalent to (2.23) since  . Hence, the claim is proved.
. Hence, the claim is proved.
By (2.23), one can obtain

Due to (2.21), we have  . Thus, the sequence
. Thus, the sequence  is a Cauchy sequence that converges to some
is a Cauchy sequence that converges to some  . By substituting
. By substituting  with
with  and
and  with
with  in (2.22), one can obtain
in (2.22), one can obtain

as  . This last condition is equivalent to saying that
. This last condition is equivalent to saying that  as
as 
References
Rzepecki B: On fixed point theorems of Maia type. Publications de l'Institut Mathématique 1980, 28(42): 179–186.
Maia MG: Un'osservazione sulle contrazioni metriche. Rendiconti del Seminario Matematico della Università di Padova 1968, 40: 139–143.
Lin SD: A common fixed point theorem in abstract spaces. Indian Journal of Pure and Applied Mathematics 1987,18(8):685–690.
Khan MS, Imdad M: A common fixed point theorem for a class of mappings. Indian Journal of Pure and Applied Mathematics 1983,14(10):1220–1227.
Huang L-G, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. Journal of Mathematical Analysis and Applications 2007,332(2):1468–1476. 10.1016/j.jmaa.2005.03.087
Rezapour Sh, Hamlbarani R: Some notes on the paper: "Cone metric spaces and fixed point theorems of contractive mappings". Journal of Mathematical Analysis and Applications 2008,345(2):719–724. 10.1016/j.jmaa.2008.04.049
Turkoglu D, Abuloha M: Cone metric spaces and fixed point theorems in diametrically contractive mappings. to appear in Acta Mathematica Sinica
Turkoglu D, Abuloha M, Abdeljawad T: KKM mappings in cone metric spaces and some fixed point theorems. Nonlinear Analysis: Theory, Methods & Applications 2010,72(1):348–353. 10.1016/j.na.2009.06.058
Şahin I, Telci M: Fixed points of contractive mappings on complete cone metric spaces. Hacettepe Journal of Mathematics and Statistics 2009,38(1):59–67.
Nieto JJ, Rodríguez-López R: Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations. Order 2005,22(3):223–239. 10.1007/s11083-005-9018-5
Nieto JJ, Rodríguez-López R: Existence and uniqueness of fixed point in partially ordered sets and applications to ordinary differential equations. Acta Mathematica Sinica 2007,23(12):2205–2212. 10.1007/s10114-005-0769-0
Nieto JJ, Pouso RL, Rodríguez-López R: Fixed point theorems in ordered abstract spaces. Proceedings of the American Mathematical Society 2007,135(8):2505–2517. 10.1090/S0002-9939-07-08729-1
Ćirić L: Fixed Point Theory Contraction Mapping principle. Faculty of Mechanical Engineering Press, Beograd, Serbia; 2003.
Suzuki T: Fixed point theorems and convergence theorems for some generalized nonexpansive mappings. Journal of Mathematical Analysis and Applications 2008,340(2):1088–1095. 10.1016/j.jmaa.2007.09.023
Turkoglu D, Abuloha M, Abdeljawad T: Some theorems and examples of cone metric spaces. to appear in Journal of Computational Analysis and Applications
Abdeljawad T: Completion of cone metric spaces. to appear in Hacettepe Journal of Mathematics and Statistics
Deimling K: Nonlinear Functional Analysis. Springer, Berlin, Germany; 1985:xiv+450.
Abdeljawad T, Karapinar E: Quasicone Metric Spaces and Generalizations of Caristi Kirk's Theorem. Fixed Point Theory and Applications 2009, 2009: 9 page.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Karapınar, E. Fixed Point Theorems in Cone Banach Spaces. Fixed Point Theory Appl 2009, 609281 (2009). https://doi.org/10.1155/2009/609281
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/609281
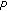 is regular if every decreasing sequence which is bounded from below is convergent.
is regular if every decreasing sequence which is bounded from below is convergent.