- Research Article
- Open access
- Published:
Existence of Solution and Positive Solution for a Nonlinear Third-Order 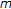 -Point BVP
-Point BVP
Fixed Point Theory and Applications volume 2010, Article number: 126192 (2010)
Abstract
In this paper, we are concerned with the following nonlinear third-order  -point boundary value problem:
-point boundary value problem:  ,
,  ,
,  ,
,  ,
,  . Some existence criteria of solution and positive solution are established by using the Schauder fixed point theorem. An example is also included to illustrate the importance of the results obtained.
. Some existence criteria of solution and positive solution are established by using the Schauder fixed point theorem. An example is also included to illustrate the importance of the results obtained.
1. Introduction
Third-order differential equations arise in a variety of different areas of applied mathematics and physics, for example, in the deflection of a curved beam having a constant or varying cross-section, a three-layer beam, electromagnetic waves, or gravity-driven flows and so on [1].
Recently, third-order two-point or three-point boundary value problems (BVPs) have received much attention from many authors; see [2–10] and the references therein. In particular, Yao [10] employed the Leray-Schauder fixed point theorem to prove the existence of solution and positive solution for the BVP

Although there are many excellent results on third-order two-point or three-point BVPs, few works have been done for more general third-order  -point BVPs [11–13]. It is worth mentioning that Jin and Lu [12] studied some third-order differential equation with the following
-point BVPs [11–13]. It is worth mentioning that Jin and Lu [12] studied some third-order differential equation with the following  -point boundary conditions:
-point boundary conditions:

The main tool used was Mawhin's continuation theorem.
Motivated greatly by [10, 12], in this paper, we investigate the following nonlinear third-order  -point BVP:
-point BVP:

Throughout, we always assume that  and
and  . The purpose of this paper is to consider the local properties of
. The purpose of this paper is to consider the local properties of  on some bounded sets and establish some existence criteria of solution and positive solution for the BVP (1.3) by using the Schauder fixed point theorem. An example is also included to illustrate the importance of the results obtained.
on some bounded sets and establish some existence criteria of solution and positive solution for the BVP (1.3) by using the Schauder fixed point theorem. An example is also included to illustrate the importance of the results obtained.
2. Main Results
Lemma 2.1.
Let  . Then, for any
. Then, for any  , the BVP
, the BVP

has a unique solution

where

Proof.
If  is a solution of the BVP (2.1), then we may suppose that
is a solution of the BVP (2.1), then we may suppose that

By the boundary conditions in (2.1), we know that

Therefore, the unique solution of the BVP (2.1)

In the remainder of this paper, we always assume that  . For convenience, we denote
. For convenience, we denote

The following theorem guarantees the existence of solution for the BVP (1.3).
Theorem 2.2.
Assume that  is continuous and there exist
is continuous and there exist  and
and  such that
such that

Then the BVP (1.3) has one solution  satisfying
satisfying

Proof.
Let  be equipped with the norm
be equipped with the norm  , where
, where  . Then
. Then  is a Banach space.
is a Banach space.
Let  ,
,  . Then the BVP (1.3) is equivalent to the following system:
. Then the BVP (1.3) is equivalent to the following system:

Furthermore, it is easy to know that the system (2.10) is equivalent to the following system:

Now, if we define an operator  by
by

where

then it is easy to see that  is completely continuous and the system (2.11) and so the BVP (1.3) is equivalent to the fixed point equation
is completely continuous and the system (2.11) and so the BVP (1.3) is equivalent to the fixed point equation

Let  . Then
. Then  is a closed convex subset of
is a closed convex subset of  . Suppose that
. Suppose that  . Then
. Then  and
and  . So,
. So,


which implies that

From (2.16) and  , we have
, we have

On the other hand, it follows from (2.17) that

In view of (2.18) and (2.19), we know that

which shows that  . Then it follows from the Schauder fixed point theorem that
. Then it follows from the Schauder fixed point theorem that  has a fixed point
has a fixed point  . In other words, the BVP (1.3) has one solution
. In other words, the BVP (1.3) has one solution  , which satisfies
, which satisfies

On the basis of Theorem 2.2, we now give some existence results of nonnegative solution and positive solution for the BVP (1.3).
Theorem 2.3.
Assume that  ,
,  ,
,  ,
,  ,
,  is continuous, and there exist
is continuous, and there exist  and
and  such that
such that

Then the BVP (1.3) has one solution  satisfying
satisfying

Proof.
Let

Then  is continuous and
is continuous and

Consider the BVP

By Theorem 2.2, we know that the BVP (2.26) has one solution  satisfying
satisfying

Since  , we get
, we get

In view of (2.28) and  , we have
, we have

which implies that

It follows from (2.28), (2.30), and the definition of  that
that

Therefore,  is a solution of the BVP (1.3) and satisfies
is a solution of the BVP (1.3) and satisfies

Corollary 2.4.
Assume that all the conditions of Theorem 2.3 are fulfilled. Then the BVP (1.3) has one positive solution if one of the following conditions is satisfied:
(i) ;
;
(ii) ;
;
(iii) ,
,  .
.
Proof.
Since it is easy to prove Cases (ii) and (iii), we only prove Case (i). It follows from Theorem 2.3 that the BVP (1.3) has a solution  , which satisfies
, which satisfies

Suppose that  . Then for any
. Then for any  , we have
, we have

which shows that  is a positive solution of the BVP (1.3).
is a positive solution of the BVP (1.3).
Example 2.5.
Consider the BVP

where  ,
,  .
.
A simple calculation shows that  and
and  . Thus, if we choose
. Thus, if we choose  and
and  , then all the conditions of Theorem 2.3 and (i) of Corollary 2.4 are fulfilled. It follows from Corollary 2.4 that the BVP (2.35) has a positive solution.
, then all the conditions of Theorem 2.3 and (i) of Corollary 2.4 are fulfilled. It follows from Corollary 2.4 that the BVP (2.35) has a positive solution.
References
Greguš M: Third Order Linear Differential Equations, Mathematics and its Applications (East European Series). Volume 22. Reidel, Dordrecht, The Netherlands; 1987:xvi+270.
Anderson DR: Green's function for a third-order generalized right focal problem. Journal of Mathematical Analysis and Applications 2003,288(1):1–14. 10.1016/S0022-247X(03)00132-X
Bai Z: Existence of solutions for some third-order boundary-value problems. Electronic Journal of Differential Equations 2008, 25: 1–6.
Feng Y, Liu S: Solvability of a third-order two-point boundary value problem. Applied Mathematics Letters 2005,18(9):1034–1040. 10.1016/j.aml.2004.04.016
Guo L-J, Sun J-P, Zhao Y-H: Existence of positive solutions for nonlinear third-order three-point boundary value problems. Nonlinear Analysis. Theory, Methods & Applications 2008,68(10):3151–3158. 10.1016/j.na.2007.03.008
Hopkins B, Kosmatov N: Third-order boundary value problems with sign-changing solutions. Nonlinear Analysis. Theory, Methods & Applications 2007,67(1):126–137. 10.1016/j.na.2006.05.003
Ma R: Multiplicity results for a third order boundary value problem at resonance. Nonlinear Analysis. Theory, Methods & Applications 1998,32(4):493–499. 10.1016/S0362-546X(97)00494-X
Sun J-P, Ren Q-Y, Zhao Y-H: The upper and lower solution method for nonlinear third-order three-point boundary value problem. Electronic Journal of Qualitative Theory of Differential Equations 2010, 26: 1–8.
Sun Y: Positive solutions for third-order three-point nonhomogeneous boundary value problems. Applied Mathematics Letters 2009,22(1):45–51. 10.1016/j.aml.2008.02.002
Yao Q: Solution and positive solution for a semilinear third-order two-point boundary value problem. Applied Mathematics Letters 2004,17(10):1171–1175. 10.1016/j.aml.2003.09.011
Du Z, Lin X, Ge W: On a third-order multi-point boundary value problem at resonance. Journal of Mathematical Analysis and Applications 2005,302(1):217–229. 10.1016/j.jmaa.2004.08.012
Jin S, Lu S: Existence of solutions for a third-order multipoint boundary value problem with -Laplacian. Journal of the Franklin Institute 2010,347(3):599–606. 10.1016/j.jfranklin.2009.12.005
Sun J-P, Zhang H-E: Existence of solutions to third-order -point boundary-value problems. Electronic Journal of Differential Equations 2008, 125: 1–9.
Acknowledgment
This paper was supported by the National Natural Science Foundation of China (10801068).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sun, JP., Jin, FX. Existence of Solution and Positive Solution for a Nonlinear Third-Order 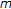 -Point BVP.
Fixed Point Theory Appl 2010, 126192 (2010). https://doi.org/10.1155/2010/126192
-Point BVP.
Fixed Point Theory Appl 2010, 126192 (2010). https://doi.org/10.1155/2010/126192
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/126192