- Research Article
- Open access
- Published:
Fixed Point Theory for Contractive Mappings Satisfying  -Maps in
-Maps in 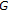 -Metric Spaces
-Metric Spaces
Fixed Point Theory and Applications volume 2010, Article number: 181650 (2010)
Abstract
We prove some fixed point results for self-mapping  in a complete
in a complete  -metric space
-metric space  under some contractive conditions related to a nondecreasing map
under some contractive conditions related to a nondecreasing map  with
with  for all
for all  . Also, we prove the uniqueness of such fixed point, as well as studying the
. Also, we prove the uniqueness of such fixed point, as well as studying the  -continuity of such fixed point.
-continuity of such fixed point.
1. Introduction
The fixed point theorems in metric spaces are playing a major role to construct methods in mathematics to solve problems in applied mathematics and sciences. So the attraction of metric spaces to a large numbers of mathematicians is understandable. Some generalizations of the notion of a metric space have been proposed by some authors. In 2006, Mustafa in collaboration with Sims introduced a new notion of generalized metric space called  -metric space [1]. In fact, Mustafa et al. studied many fixed point results for a self-mapping in
-metric space [1]. In fact, Mustafa et al. studied many fixed point results for a self-mapping in  -metric space under certain conditions; see[1–5]. In the present work, we study some fixed point results for self-mapping in a complete
-metric space under certain conditions; see[1–5]. In the present work, we study some fixed point results for self-mapping in a complete  -metric space
-metric space  under some contractive conditions related to a nondecreasing map
under some contractive conditions related to a nondecreasing map  with
with  for all
for all  .
.
2. Basic Concepts
In this section, we present the necessary definitions and theorems in  -metric spaces.
-metric spaces.
Definition 2.1 (see [1]).
Let  be a nonempty set and let
be a nonempty set and let  be a function satisfying the following properties:
be a function satisfying the following properties:
(1)
 if
if  ;
;
(2) , for all
, for all  with
with  ;
;
(3) for all
for all  with
with  ;
;
(4) , symmetry in all three variables;
, symmetry in all three variables;
(5) for all
for all  .
.
Then the function  is called a generalized metric, or, more specifically, a
is called a generalized metric, or, more specifically, a  -metric on
-metric on  , and the pair
, and the pair  is called a
is called a  -metric space.
-metric space.
Definition 2.2 (see [1]).
Let  be a
be a  -metric space, and let
-metric space, and let  be a sequence of points of
be a sequence of points of  , a point
, a point  is said to be the limit of the sequence
is said to be the limit of the sequence  , if
, if  , and we say that the sequence
, and we say that the sequence  is
is  -convergent to
-convergent to  or
or 
 -converges to
-converges to  .
.
Thus,  in a
in a  -metric space
-metric space  if for any
if for any  , there exists
, there exists  such that
such that  for all
for all  .
.
Proposition 2.3 (see [1]).
Let  be a
be a  -metric space. Then the following are equivalent.
-metric space. Then the following are equivalent.
(1) is
is  -convergent to
-convergent to  .
.
(2) as
as  .
.
(3) as
as  .
.
(4) as
as  .
.
Definition 2.4 (see [1]).
Let  be a
be a  -metric space; a sequence
-metric space; a sequence  is called
is called  -Cauchy if for every
-Cauchy if for every  , there is
, there is  such that
such that  , for all
, for all  ; that is,
; that is,  as
as 
Proposition 2.5 (see [3]).
Let  be a
be a  -metric space. Then the following are equivalent.
-metric space. Then the following are equivalent.
(1)The sequence  is
is  -Cauchy.
-Cauchy.
(2)For every  , there is
, there is  such that
such that  , for all
, for all  .
.
Definition 2.6 (see [1]).
Let  and
and  be
be  -metric spaces, and let
-metric spaces, and let  be a function. Then
be a function. Then  is said to be
is said to be  -continuous at a point
-continuous at a point  if and only if for every
if and only if for every  , there is
, there is  such that
such that  and
and  implies
implies  . A function
. A function  is
is  -continuous at
-continuous at  if and only if it is
if and only if it is  -continuous at all
-continuous at all  .
.
Proposition 2.7 (see [1]).
Let  and
and  be
be  -metric spaces. Then
-metric spaces. Then  is
is  -continuous at
-continuous at  if and only if it is
if and only if it is  -sequentially continuous at
-sequentially continuous at  ; that is, whenever
; that is, whenever  is
is  -convergent to
-convergent to  ,
,  is
is  -convergent to
-convergent to  .
.
Proposition 2.8 (see [1]).
Let  be a
be a  -metric space. Then the function
-metric space. Then the function  is jointly continuous in all three of its variables.
is jointly continuous in all three of its variables.
The following are examples of  -metric spaces.
-metric spaces.
Example 2.9 (see [1]).
Let  be the usual metric space. Define
be the usual metric space. Define  by
by

for all  . Then it is clear that
. Then it is clear that  is a
is a  -metric space.
-metric space.
Example 2.10 (see [1]).
Let  . Define
. Define  on
on  by
by

and extend  to
to  by using the symmetry in the variables. Then it is clear that
by using the symmetry in the variables. Then it is clear that  is a
is a  -metric space.
-metric space.
Definition 2.11 (see [1]).
A  -metric space
-metric space  is called
is called  -complete if every
-complete if every  -Cauchy sequence in
-Cauchy sequence in  is
is  -convergent in
-convergent in  .
.
3. Main Results
Following to Matkowski [6], let  be the set of all functions
be the set of all functions  such that
such that  be a nondecreasing function with
be a nondecreasing function with  for all
for all  . If
. If  , then
, then  is called
is called  -map. If
-map. If  is
is  -map, then it is an easy matter to show that
-map, then it is an easy matter to show that
(1) for all
for all  ;
;
(2) .
.
From now unless otherwise stated we mean by  the
the  -map. Now, we introduce and prove our first result.
-map. Now, we introduce and prove our first result.
Theorem 3.1.
Let  be a complete
be a complete  -metric space. Suppose the map
-metric space. Suppose the map  satisfies
satisfies

for all  . Then
. Then  has a unique fixed point (say
has a unique fixed point (say  ) and
) and  is
is  -continuous at
-continuous at  .
.
Proof.
Choose  . Let
. Let  ,
,  . Assume
. Assume  , for each
, for each  . Claim
. Claim  is a
is a  -Cauchy sequence in
-Cauchy sequence in  : for
: for  , we have
, we have

given  , since
, since  and
and  , there is an integer
, there is an integer  such that
such that

Hence

For  with
with  , we claim that
, we claim that

We prove Inequality (3.5) by induction on  . Inequality (3.5) holds for
. Inequality (3.5) holds for  by using Inequality (3.4) and the fact that
by using Inequality (3.4) and the fact that  . Assume Inequality (3.5) holds for
. Assume Inequality (3.5) holds for  . For
. For  , we have
, we have

By induction on  , we conclude that Inequality (3.5) holds for all
, we conclude that Inequality (3.5) holds for all  . So
. So  is
is  -Cauchy and hence
-Cauchy and hence  is
is  -convergent to some
-convergent to some  . For
. For  , we have
, we have

Letting  , and using the fact that
, and using the fact that  is continuous on its variable, we get that
is continuous on its variable, we get that  . Hence
. Hence  . So
. So  is a fixed point of
is a fixed point of  . Now, let
. Now, let  be another fixed point of
be another fixed point of  with
with  . Since
. Since  is a
is a  -map, we have
-map, we have

which is a contradiction. So  , and hence
, and hence  has a unique fixed point. To Show that
has a unique fixed point. To Show that  is
is  -continuous at
-continuous at  , let
, let  be any sequence in
be any sequence in  such that
such that  is
is  -convergent to
-convergent to  . For
. For  , we have
, we have

Letting  , we get
, we get  . Hence
. Hence  is
is  -convergent to
-convergent to  . So
. So  is
is  -continuous at u.
-continuous at u.
As an application of Theorem 3.1, we have the following results.
Corollary 3.2.
Let  be a complete
be a complete  -metric space. Suppose that the map
-metric space. Suppose that the map  satisfies for
satisfies for  :
:

for all  . Then
. Then  has a unique fixed point (say
has a unique fixed point (say  ).
).
Proof.
From Theorem 3.1, we conclude that  has a unique fixed point say
has a unique fixed point say  . Since
. Since

we have that  is also a fixed point to
is also a fixed point to  . By uniqueness of
. By uniqueness of  , we get
, we get  .
.
Corollary 3.3.
Let  be a complete
be a complete  -metric space. Suppose that the map
-metric space. Suppose that the map  satisfies
satisfies

for all  . Then
. Then  has a unique fixed point (say
has a unique fixed point (say  ) and
) and  is
is  -continuous at
-continuous at  .
.
Proof.
follows from Theorem 3.1 by taking  .
.
Corollary 3.4.
Let  be a complete
be a complete  -metric space. Suppose there is
-metric space. Suppose there is  such that the map
such that the map  satisfies
satisfies

for all  . Then
. Then  has a unique fixed point (say
has a unique fixed point (say  ) and
) and  is
is  -continuous at
-continuous at  .
.
Proof.
Define  by
by  . Then it is clear that
. Then it is clear that  is a nondecreasing function with
is a nondecreasing function with  for all
for all  . Since
. Since

the result follows from Theorem 3.1.
The above corollary has been stated in [7, Theorem 5.1.7], and proved by a different way.
Corollary 3.5.
Let  be a complete
be a complete  -metric space. Suppose the map
-metric space. Suppose the map  satisfies
satisfies

for all  . Then
. Then  has a unique fixed point (say
has a unique fixed point (say  ) and
) and  is
is  -continuous at
-continuous at  .
.
Proof.
Define  by
by  . Then it is clear that
. Then it is clear that  is a nondecreasing function with
is a nondecreasing function with  for all
for all  . Since
. Since

the result follows from Theorem 3.1.
Theorem 3.6.
Let  be a complete
be a complete  -metric space. Suppose that the map
-metric space. Suppose that the map  satisfies
satisfies

for all  . Then
. Then  has a unique fixed point (say
has a unique fixed point (say  ) and
) and  is
is  -continuous at
-continuous at  .
.
Proof.
Choose  . Let
. Let  ,
,  . Assume
. Assume  , for each
, for each  . Thus for
. Thus for  , we have
, we have

If

then

which is impossible. So it must be the case that

and hence

Thus for  , we have
, we have

The same argument is similar to that in proof of Theorem 3.1; one can show that  is a
is a  -Cauchy sequence. Since
-Cauchy sequence. Since  is
is  -complete, we conclude that
-complete, we conclude that  is
is  -convergent to some
-convergent to some  . For
. For  , we have
, we have

Case 1.

then we have

Letting  , we conclude that
, we conclude that  , and hence
, and hence  .
.
Case 2.

then we have

Letting  , we conclude that
, we conclude that  , and hence
, and hence  .
.
Case 3.

then we have

Letting  , we conclude that
, we conclude that  , and hence
, and hence  . In all cases, we conclude that
. In all cases, we conclude that  is a fixed point of
is a fixed point of  . Let
. Let  be any other fixed point of
be any other fixed point of  such that
such that  . Then
. Then

which is a contradiction since  . Therefore,
. Therefore,  and hence
and hence  . To show that
. To show that  is
is  -continuous at
-continuous at  , let
, let  be any sequence in
be any sequence in  such that
such that  is
is  -convergent to
-convergent to  . Then
. Then

Let  , we get that
, we get that  is
is  -convergent to
-convergent to  . Hence
. Hence  is
is  -continuous at
-continuous at  .
.
As an application to Theorem 3.6, we have the following results.
Corollary 3.7.
Let  be a complete
be a complete  -metric space. Suppose there is
-metric space. Suppose there is  such that the map
such that the map  satisfies
satisfies

for all  . Then
. Then  has a unique fixed point (say
has a unique fixed point (say  ) and
) and  is
is  -continuous at
-continuous at  .
.
Proof.
Define  by
by  . Then it is clear that
. Then it is clear that  is a nondecreasing function with
is a nondecreasing function with  for all
for all  . Since
. Since

for all  the result follows from Theorem 3.6.
the result follows from Theorem 3.6.
Corollary 3.8.
Let  be a complete
be a complete  -metric space. Suppose that the map
-metric space. Suppose that the map  satisfies:
satisfies:

for all  . Then
. Then  has a unique fixed point (say
has a unique fixed point (say  ) and
) and  is
is  -continuous at
-continuous at  .
.
Proof.
It follows from Theorem 3.6 by replacing  .
.
References
Mustafa Z, Sims B: A new approach to generalized metric spaces. Journal of Nonlinear and Convex Analysis 2006,7(2):289–297.
Mustafa Z, Obiedat H, Awawdeh F: Some fixed point theorem for mapping on complete
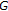 -metric spaces Fixed Point Theory and Applications 2008, 2008:-12.
-metric spaces Fixed Point Theory and Applications 2008, 2008:-12.Mustafa Z, Sims B: Some remarks concerning -metric spaces. In Proceedings of the International Conference on Fixed Point Theory and Applications, 2004, Yokohama, Japan. Yokohama; 189–198.
Mustafa Z, Sims B: Fixed point theorems for contractive mappings in complete
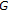 -metric spaces Fixed Point Theory and Applications 2009, 2009:-10.
-metric spaces Fixed Point Theory and Applications 2009, 2009:-10.Mustafa Z, Shatanawi W, Bataineh M: Existence of fixed point results in
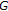 -metric spaces International Journal of Mathematics and Mathematical Sciences 2009, 2009:-10.
-metric spaces International Journal of Mathematics and Mathematical Sciences 2009, 2009:-10.Matkowski J: Fixed point theorems for mappings with a contractive iterate at a point. Proceedings of the American Mathematical Society 1977,62(2):344–348. 10.1090/S0002-9939-1977-0436113-5
Mustafa Z: A new structure for generalized metric spaces with applications to fixed point theory, Ph.D. thesis. University of Newcastle, Newcastle, UK; 2005.
Acknowledgments
The author would like to thank the editor of the paper and the referees for their precise remarks to improve the presentation of the paper. This paper is financially supported by the Deanship of the Academic Research at the Hashemite University, Zarqa, Jordan.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Shatanawi, W. Fixed Point Theory for Contractive Mappings Satisfying  -Maps in
-Maps in 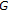 -Metric Spaces.
Fixed Point Theory Appl 2010, 181650 (2010). https://doi.org/10.1155/2010/181650
-Metric Spaces.
Fixed Point Theory Appl 2010, 181650 (2010). https://doi.org/10.1155/2010/181650
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/181650
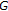 -metric spaces Fixed Point Theory and Applications 2008, 2008:-12.
-metric spaces Fixed Point Theory and Applications 2008, 2008:-12.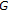 -metric spaces Fixed Point Theory and Applications 2009, 2009:-10.
-metric spaces Fixed Point Theory and Applications 2009, 2009:-10.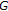 -metric spaces International Journal of Mathematics and Mathematical Sciences 2009, 2009:-10.
-metric spaces International Journal of Mathematics and Mathematical Sciences 2009, 2009:-10.