- Research Article
- Open access
- Published:
Measures of Noncircularity and Fixed Points of Contractive Multifunctions
Fixed Point Theory and Applications volume 2010, Article number: 340631 (2010)
Abstract
In analogy to the Eisenfeld-Lakshmikantham measure of nonconvexity and the Hausdorff measure of noncompactness, we introduce two mutually equivalent measures of noncircularity for Banach spaces satisfying a Cantor type property, and apply them to establish a fixed point theorem of Darbo type for multifunctions. Namely, we prove that every multifunction with closed values, defined on a closed set and contractive with respect to any one of these measures, has the origin as a fixed point.

1. Introduction
Let  be a Banach space over the field
be a Banach space over the field  . In what follows, we write
. In what follows, we write  for the closed unit ball of
for the closed unit ball of  . Denote by
. Denote by  the collection of all subsets of
the collection of all subsets of  and consider
and consider

For  , define their nonsymmetric Hausdorff distance by
, define their nonsymmetric Hausdorff distance by

and their symmetric Hausdorff distance (or Hausdorff-Pompeiu distance) by

This  is a pseudometric on
is a pseudometric on  , since
, since

where  denotes the closure of
denotes the closure of  .
.
Around 1955, Darbo [1] ensured the existence of fixed points for so-called condensing operators on Banach spaces, a result which generalizes both Schauder fixed point theorem and Banach contractive mapping principle. More precisely, Darbo proved that if  is closed and convex,
is closed and convex,  is a measure of noncompactness, and
is a measure of noncompactness, and  is continuous and
is continuous and  -contractive, that is,
-contractive, that is,  for some
for some  , then
, then  has a fixed point. Below we recall the axiomatic definition of a regular measure of noncompactness on
has a fixed point. Below we recall the axiomatic definition of a regular measure of noncompactness on  ; we refer to [2] for details.
; we refer to [2] for details.
Definition 1.1.
A function  will be called a regular measure of noncompactness if
will be called a regular measure of noncompactness if  satisfies the following axioms, for
satisfies the following axioms, for  , and
, and  :
:
(1) if, and only if,
if, and only if,  is compact.
is compact.
(2) , where
, where  denotes the convex hull of
denotes the convex hull of  .
.
(3)(monotonicity)  implies
implies  .
.
(4)(maximum property)  .
.
(5)(homogeneity)  .
.
(6)(subadditivity)  .
.
A regular measure of noncompactness  possesses the following properties:
possesses the following properties:
(1) , where
, where

is the diameter of  (cf. [2, Theorem 3.2.1]).
(cf. [2, Theorem 3.2.1]).
(2)(Hausdorff continuity)  [2, page 12].
[2, page 12].
-
(3)
(Cantor property) If
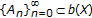 is a decreasing sequence of closed sets with
is a decreasing sequence of closed sets with  , then
, then 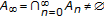 , and
, and 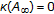 [3, Lemma 2.1].
[3, Lemma 2.1].
In Sections 2 and 3 of this paper we introduce two mutually equivalent measures of noncircularity, the kernel (that is, the class of sets which are mapped to 0) of any of them consisting of all those  such that
such that  is balanced. Recall that
is balanced. Recall that  is balanced provided that
is balanced provided that  for all
for all  with
with  . For example, in
. For example, in  the only bounded balanced sets are the open or closed intervals centered at the origin. Similarly, in
the only bounded balanced sets are the open or closed intervals centered at the origin. Similarly, in  as a complex vector space the only bounded balanced sets are the open or closed disks centered at the origin, while in
as a complex vector space the only bounded balanced sets are the open or closed disks centered at the origin, while in  as a real vector space there are many more bounded balanced sets, namely all those bounded sets which are symmetric with respect to the origin.
as a real vector space there are many more bounded balanced sets, namely all those bounded sets which are symmetric with respect to the origin.
Denoting by  either one of the two measures introduced, in Section 4 we prove a result of Darbo type for
either one of the two measures introduced, in Section 4 we prove a result of Darbo type for  -contractive multimaps (see Section 4 for precise definitions). It is shown that the origin is a fixed point of every
-contractive multimaps (see Section 4 for precise definitions). It is shown that the origin is a fixed point of every  -contractive multimap
-contractive multimap  with closed values defined on a closed set
with closed values defined on a closed set  such that
such that  .
.
2. The E-L Measure of Noncircularity
The definition of the Eisenfeld-Lakshmikantham measure of nonconvexity [4] motivates the following.
Definition 2.1.
For  , set
, set

where  denotes the balanced hull of
denotes the balanced hull of  , that is,
, that is,

By analogy with the Eisenfeld-Lakshmikantham measure of nonconvexity, we shall refer to  as the E-L measure of noncircularity.
as the E-L measure of noncircularity.
Next we gather some properties of  which justify such a denomination. Their proofs are fairly direct, but we include them for the sake of completeness.
which justify such a denomination. Their proofs are fairly direct, but we include them for the sake of completeness.
Proposition 2.2.
In the above notation, for  , and
, and  , the following hold:
, the following hold:
(1) if, and only if,
if, and only if,  is balanced.
is balanced.
(2) .
.
(3) .
.
(4) .
.
(5) .
.
(6) , where
, where

is the norm of  . In particular, if
. In particular, if  then
then  , where
, where

is the diameter of  .
.
(7) .
.
Proof.
Let  denote the closed balanced hull of
denote the closed balanced hull of  . The identity
. The identity

holds. Indeed,  implies
implies  . Conversely,
. Conversely,  implies
implies  .
.
(1)By definition,  if, and only if,
if, and only if,  or, equivalently,
or, equivalently,  . This means that
. This means that  , which by (2.5) occurs if, and only if,
, which by (2.5) occurs if, and only if,  is balanced.
is balanced.
(2)In view of (1.4) and (2.5),

It only remains to prove that  . Suppose
. Suppose  , so that
, so that  . The set
. The set  being convex, it follows that
being convex, it follows that  , whence
, whence  . From the arbitrariness of
. From the arbitrariness of  we conclude that
we conclude that  .
.
(3)Assume  , that is,
, that is,  and
and  . Then
. Then  ,
,  , and the fact that
, and the fact that  is a balanced set containing
is a balanced set containing  , imply
, imply

whence  . The arbitrariness of
. The arbitrariness of  yields
yields  .
.
(4)For  , this is obvious. Suppose
, this is obvious. Suppose  . If
. If  then
then  , whence
, whence  . Thus
. Thus  , and from the arbitrariness of
, and from the arbitrariness of  we infer that
we infer that  . Conversely, assume
. Conversely, assume  . Then
. Then  , whence
, whence  . Therefore
. Therefore  , and from the arbitrariness of
, and from the arbitrariness of  we conclude that
we conclude that  .
.
(5)Let  and choose
and choose  such that
such that  ,
,  and
and  . Then
. Then  ,
,  and the fact that
and the fact that  is a balanced set containing
is a balanced set containing  , imply
, imply  , so that
, so that  . The arbitrariness of
. The arbitrariness of  yields
yields  .
.
(6)Pick  , with
, with  and
and  , and let
, and let  . As
. As

we obtain

where for the validity of the latter estimate we have assumed  .
.
(7)It is enough to show that

since then, by symmetry,

whence the desired result. Now

To complete the proof we will establish that  . Indeed, suppose
. Indeed, suppose  , and let
, and let  , with
, with  and
and  . Then there exists
. Then there exists  such that
such that  . Consequently, for
. Consequently, for  we have
we have

This means that  , so that
, so that  . From the arbitrariness of
. From the arbitrariness of  we conclude that
we conclude that  .
.
Remark 2.3.
The identity  may not hold, as can be seen by choosing
may not hold, as can be seen by choosing  . In fact,
. In fact,  is balanced, while
is balanced, while  is not. Therefore,
is not. Therefore,  .
.
In general, the identity  does not hold either. To show this, choose
does not hold either. To show this, choose  and
and  , respectively, as the upper and lower closed half unit disks of the complex plane. Then
, respectively, as the upper and lower closed half unit disks of the complex plane. Then  equals the closed unit disk, which is balanced, while
equals the closed unit disk, which is balanced, while  ,
,  are not. Thus,
are not. Thus,  .
.
Note that  is not monotone: from
is not monotone: from  and
and  , it does not necessarily follow that
, it does not necessarily follow that  . Otherwise,
. Otherwise,  would imply
would imply  , which is plainly false since not every subset of a balanced set is balanced.
, which is plainly false since not every subset of a balanced set is balanced.
3. The Hausdorff Measure of Noncircularity
The following definition is motivated by that of the Hausdorff measure of noncompactness (cf. [2, Theorem 2.1]).
Definition 3.1.
We define the Hausdorff measure of noncircularity of  by
by

where  denotes the class of all balanced sets in
denotes the class of all balanced sets in  .
.
In general,  , as the next example shows.
, as the next example shows.
Example 3.2.
Let  . Then
. Then  , and
, and

If  is any closed bounded balanced set in
is any closed bounded balanced set in  , we have
, we have

so that

Since

we obtain

Thus,  .
.
Next we compare the measures  and
and  and establish some properties for the latter. Again, most proofs derive directly from the definitions, but we include them for completeness.
and establish some properties for the latter. Again, most proofs derive directly from the definitions, but we include them for completeness.
Proposition 3.3.
In the above notation, for  , and
, and  , the following hold:
, the following hold:
(1) , and the estimates are sharp.
, and the estimates are sharp.
(2) if, and only if,
if, and only if,  is balanced.
is balanced.
(3) .
.
(4) .
.
(5) .
.
(6) .
.
(7) , where
, where

is the norm of  . In particular, if
. In particular, if  then
then  , where
, where

is the diameter of  .
.
(8) .
.
Proof.
-
(1)
That
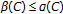 follows immediately from the definitions of
follows immediately from the definitions of  and
and  . Let
. Let 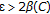 and choose
and choose 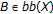 satisfying
satisfying 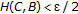 , so that
, so that 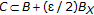 and
and  . Then
. Then  and
and  , thus proving that
, thus proving that 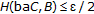 . Now
. Now 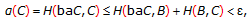 (3.9)
(3.9)
and the arbitrariness of  yields
yields  . Example 3.2 shows that this estimate is sharp. In order to exhibit a set
. Example 3.2 shows that this estimate is sharp. In order to exhibit a set  such that
such that  , let
, let  . Then
. Then  , and
, and

On the other hand, let  be any closed bounded balanced subset of
be any closed bounded balanced subset of  . For a fixed
. For a fixed  , there holds
, there holds

Therefore,

so that

-
(2)
Let
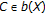 . As we just proved,
. As we just proved, 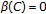 if, and only if,
if, and only if, 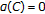 . In view of Proposition 2.2, this occurs if, and only if,
. In view of Proposition 2.2, this occurs if, and only if,  is balanced.
is balanced. -
(3)
By (1.4), there holds
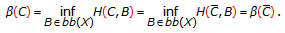 (3.14)
(3.14)
Now we only need to show that  . Assuming
. Assuming  , choose
, choose  for which
for which  , so that
, so that

The sum of convex sets being convex, we infer

Since  is balanced we obtain
is balanced we obtain  and, as
and, as  is arbitrary, we conclude that
is arbitrary, we conclude that  .
.
-
(4)
Suppose
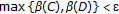 , that is,
, that is, 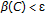 and
and 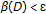 . Pick
. Pick 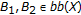 satisfying
satisfying 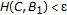 and
and 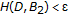 . Then
. Then 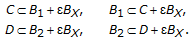 (3.17)
(3.17)
Thus we get

whence  and,
and,  being balanced, also
being balanced, also  . From the arbitrariness of
. From the arbitrariness of  we conclude that
we conclude that  .
.
-
(5)
If
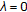 , the property is obvious. Assume
, the property is obvious. Assume 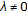 . Given
. Given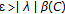 , there exists
, there exists 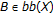 such that
such that 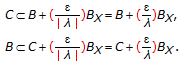 (3.19)
(3.19)
Then

so that  . Since
. Since  is balanced, it follows that
is balanced, it follows that  and,
and,  being arbitrary, we obtain
being arbitrary, we obtain  . Conversely, let
. Conversely, let  . Then there exists
. Then there exists  such that
such that

Hence,

Therefore,  . Since
. Since  is balanced we conclude that
is balanced we conclude that  , or
, or  . The arbitrariness of
. The arbitrariness of  finally yields
finally yields  .
.
-
(6)
Let
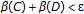 and let
and let 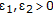 satisfy
satisfy  ,
, 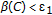 and
and  . Choose
. Choose 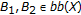 such that
such that 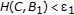 and
and 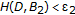 . Then
. Then 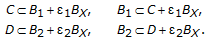 (3.23)
(3.23)
Thus we obtain

whence  and,
and,  being balanced, also
being balanced, also  . From the arbitrariness of
. From the arbitrariness of  we conclude that
we conclude that  .
.
-
(7)
This follows from Proposition 2.2.
-
(8)
For
 there holds
there holds 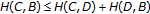 , whence
, whence 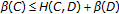 . Therefore,
. Therefore,  . By symmetry,
. By symmetry, 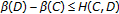 , thus yielding
, thus yielding 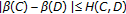 , as claimed.
, as claimed.
Remark 3.4.
By the same reasons as  , the measure
, the measure  fails to be monotone and, in general, the identities
fails to be monotone and, in general, the identities  and
and

do not hold (cf. Remark 2.3).
4. A Fixed Point Theorem for Multimaps
The study of fixed points for multivalued mappings was initiated by Kakutani [5] in 1941 in finite dimensional spaces and extended to infinite dimensional Banach spaces by Bohnenblust and Karlin [6] in 1950 and to locally convex spaces by Fan [7] in 1952. Since then, it has become a very active area of research, both from the theoretical point of view and in applications. In this section we use the previous theory to obtain a fixed point theorem for multifunctions in the Banach space  . We begin by recalling some definitions.
. We begin by recalling some definitions.
Definition 4.1.
Let  . A multimap or multifunction
. A multimap or multifunction  from
from  to the class
to the class  of all nonempty subsets of a given set
of all nonempty subsets of a given set  , written
, written  , is any map from
, is any map from  to
to  .
.
If  is a multifunction and
is a multifunction and  , then
, then

Definition 4.2.
Given  , let
, let  , and let
, and let  represent any of the two measures of noncircularity introduced above. A fixed point of
represent any of the two measures of noncircularity introduced above. A fixed point of  is a point
is a point  such that
such that  . The multifunction
. The multifunction  will be called
will be called
(i)a  -contraction (of constant
-contraction (of constant  ), if
), if

for some  ;
;
(ii)a  -contraction, if
-contraction, if

where  is a comparison function, that is,
is a comparison function, that is,  is increasing,
is increasing,  , and
, and  as
as  for each
for each  .
.
Note that a  -contraction of constant
-contraction of constant  corresponds to a
corresponds to a  -contraction with
-contraction with  .
.
In order to establish our main result, we prove a property of Cantor type for the E-L and Hausdorff measures of noncircularity.
Proposition 4.3.
Let  be a Banach space and
be a Banach space and  a decreasing sequence of closed sets such that
a decreasing sequence of closed sets such that  , where
, where  denotes either
denotes either  or
or  . Then the set
. Then the set

satisfies

Hence  belongs to
belongs to  and is closed and balanced.
and is closed and balanced.
Proof.
By Proposition 3.3 we have  if, and only if,
if, and only if,  . Thus for the proof it suffices to set
. Thus for the proof it suffices to set  .
.
Since  , necessarily
, necessarily

Conversely, let  . As
. As  , to every
, to every  there corresponds
there corresponds  such that
such that  ,
,  implies
implies  . This yields an increasing sequence
. This yields an increasing sequence  of positive integers and vectors
of positive integers and vectors  which satisfy
which satisfy  . Thus the sequence
. Thus the sequence  converges to
converges to  as
as  . Moreover, since
. Moreover, since  and
and  is closed, we find that
is closed, we find that  . In other words,
. In other words,  . This proves (4.5).
. This proves (4.5).
Note that  implies
implies  , whence
, whence  . Since the intersection of closed, bounded and balanced sets preserves those properties, so does
. Since the intersection of closed, bounded and balanced sets preserves those properties, so does  .
.
Remark 4.4.
In contrast to Proposition 4.3, the Eisenfeld-Lakshmikantham measure of nonconvexity does not necessarily satisfy a Cantor property. Indeed, in real, nonreflexive Banach spaces one can find a decreasing sequence  of nonempty, closed, bounded, convex sets with empty intersection. To construct such a sequence, just take a unitary continuous linear functional
of nonempty, closed, bounded, convex sets with empty intersection. To construct such a sequence, just take a unitary continuous linear functional  in a real, nonreflexive Banach space
in a real, nonreflexive Banach space  which fails to be norm-attaining on the closed unit ball
which fails to be norm-attaining on the closed unit ball  of
of  (the existence of such an
(the existence of such an  is guaranteed by a classical, well-known theorem of James, cf. [8]), and define
is guaranteed by a classical, well-known theorem of James, cf. [8]), and define

Now we are in a position to derive the announced result. Here, and in the sequel,  will stand for any one of the measures of noncircularity
will stand for any one of the measures of noncircularity  or
or  .
.
Theorem 4.5.
Let  be a Banach space, and let
be a Banach space, and let  be closed. If
be closed. If  is a
is a  -contraction with closed values, then
-contraction with closed values, then  and 0 is a fixed point of
and 0 is a fixed point of  .
.
Proof.
Our hypotheses imply

Setting  , from Propositions 2.2 and 3.3 we find that
, from Propositions 2.2 and 3.3 we find that  is a decreasing sequence of closed sets with
is a decreasing sequence of closed sets with  . Proposition 4.3 shows that
. Proposition 4.3 shows that  is a nonempty, balanced subset of
is a nonempty, balanced subset of  ; in particular,
; in particular,  . Now,
. Now,  being balanced, we have
being balanced, we have

whence  . This shows that the nonempty set
. This shows that the nonempty set  is balanced and forces
is balanced and forces  , as asserted.
, as asserted.
Corollary 4.6.
Let  be a Banach space, and let
be a Banach space, and let  be closed. If
be closed. If  is a
is a  -contraction with closed values, then
-contraction with closed values, then  and 0 is a fixed point of
and 0 is a fixed point of  .
.
Proof.
It suffices to apply Theorem 4.5, with  , for
, for  .
.
References
Darbo G: Punti uniti in trasformazioni a codominio non compatto. Rendiconti del Seminario Matematico della Università di Padova 1955, 24: 84–92.
Banaś J, Goebel K: Measures of Noncompactness in Banach Spaces, Lecture Notes in Pure and Applied Mathematics. Volume 60. Marcel Dekker, New York, NY, USA; 1980:vi+97.
Banaś J, Szynal D, Wędrychowicz S: On existence, asymptotic behaviour and stability of solutions of stochastic integral equations. Stochastic Analysis and Applications 1991,9(4):363–385. 10.1080/07362999108809246
Eisenfeld J, Lakshmikantham V: On a measure of nonconvexity and applications. Yokohama Mathematical Journal 1976,24(1–2):133–140.
Kakutani S: A generalization of Brouwer's fixed point theorem. Duke Mathematical Journal 1941,8(3):457–459. 10.1215/S0012-7094-41-00838-4
Bohnenblust HF, Karlin S: On a theorem of Ville. In Contributions to the Theory of Games. Edited by: Kuhn HW, Tucker AW. Princeton University Press, Princeton, NJ, USA; 1950:155–160.
Fan K: Fixed-point and minimax theorems in locally convex topological linear spaces. Proceedings of the National Academy of Sciences of the United States of America 1952,38(2):121–126. 10.1073/pnas.38.2.121
James RC: Reflexivity and the sup of linear functionals. Israel Journal of Mathematics 1972,13(3–4):289–300. 10.1007/BF02762803
Acknowledgments
This paper has been partially supported by ULL (MGC grants) and MEC-FEDER (MTM2007-65604, MTM2007-68114). It is dedicated to Professor A. Martinón on the occasion of his 60th birthday. The author is grateful to Professor J. Banaś for his interest in this work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Marrero, I. Measures of Noncircularity and Fixed Points of Contractive Multifunctions. Fixed Point Theory Appl 2010, 340631 (2010). https://doi.org/10.1155/2010/340631
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/340631
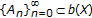 is a decreasing sequence of closed sets with
is a decreasing sequence of closed sets with  , then
, then 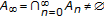 , and
, and 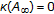 [
[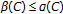 follows immediately from the definitions of
follows immediately from the definitions of  and
and  . Let
. Let 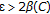 and choose
and choose 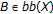 satisfying
satisfying 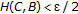 , so that
, so that 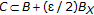 and
and  . Then
. Then  and
and  , thus proving that
, thus proving that 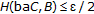 . Now
. Now 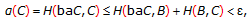
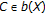 . As we just proved,
. As we just proved, 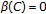 if, and only if,
if, and only if, 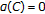 . In view of Proposition 2.2, this occurs if, and only if,
. In view of Proposition 2.2, this occurs if, and only if,  is balanced.
is balanced.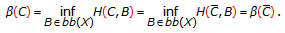
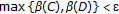 , that is,
, that is, 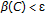 and
and 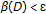 . Pick
. Pick 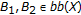 satisfying
satisfying 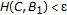 and
and 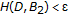 . Then
. Then 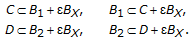
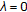 , the property is obvious. Assume
, the property is obvious. Assume 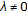 . Given
. Given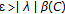 , there exists
, there exists 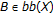 such that
such that 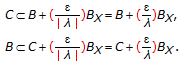
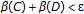 and let
and let 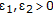 satisfy
satisfy  ,
, 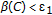 and
and  . Choose
. Choose 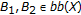 such that
such that 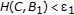 and
and 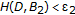 . Then
. Then 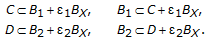
 there holds
there holds 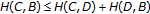 , whence
, whence 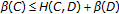 . Therefore,
. Therefore,  . By symmetry,
. By symmetry, 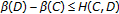 , thus yielding
, thus yielding 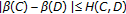 , as claimed.
, as claimed.