- Research Article
- Open access
- Published:
New Iterative Approximation Methods for a Countable Family of Nonexpansive Mappings in Banach Spaces
Fixed Point Theory and Applications volume 2011, Article number: 671754 (2011)
Abstract
We introduce new general iterative approximation methods for finding a common fixed point of a countable family of nonexpansive mappings. Strong convergence theorems are established in the framework of reflexive Banach spaces which admit a weakly continuous duality mapping. Finally, we apply our results to solve the the equilibrium problems and the problem of finding a zero of an accretive operator. The results presented in this paper mainly improve on the corresponding results reported by many others.
1. Introduction
In recent years, the existence of common fixed points for a finite family of nonexpansive mappings has been considered by many authors (see [1–4] and the references therein). The well-known convex feasibility problem reduces to finding a point in the intersection of the fixed point sets of a family of nonexpansive mappings (see [5, 6]). The problem of finding an optimal point that minimizes a given cost function over the common set of fixed points of a family of nonexpansive mappings is of wide interdisciplinary interest and practical importance (see [2, 7]). A simple algorithmic solution to the problem of minimizing a quadratic function over the common set of fixed points of a family of nonexpansive mappings is of extreme value in many applications including set theoretic signal estimation (see [7, 8]).
Let  be a normed linear space. Recall that a mapping
be a normed linear space. Recall that a mapping  is called nonexpansive if
is called nonexpansive if

We use  to denote the set of fixed points of
to denote the set of fixed points of  , that is,
, that is,  . A self mapping
. A self mapping  is a contraction on
is a contraction on  if there exists a constant
if there exists a constant  such that
such that

One classical way to study nonexpansive mappings is to use contractions to approximate a nonexpansive mapping [9–11]. More precisely, take  and define a contraction
and define a contraction  by
by

where  is a fixed point. Banach's contraction mapping principle guarantees that
is a fixed point. Banach's contraction mapping principle guarantees that  has a unique fixed point
has a unique fixed point  in
in  . It is unclear, in general, what is the behavior of
. It is unclear, in general, what is the behavior of  as
as  , even if
, even if  has a fixed point. However, in the case of
has a fixed point. However, in the case of  having a fixed point, Browder [9] proved that if
having a fixed point, Browder [9] proved that if  is a Hilbert space, then
is a Hilbert space, then  converges strongly to a fixed point of
converges strongly to a fixed point of  . Reich [10] extended Browder's result to the setting of Banach spaces and proved that if
. Reich [10] extended Browder's result to the setting of Banach spaces and proved that if  is a uniformly smooth Banach space, then
is a uniformly smooth Banach space, then  converges strongly to a fixed point of
converges strongly to a fixed point of  and the limit defines the (unique) sunny nonexpansive retraction from
and the limit defines the (unique) sunny nonexpansive retraction from  onto
onto  . Xu [11] proved Reich's results hold in reflexive Banach spaces which have a weakly continuous duality mapping.
. Xu [11] proved Reich's results hold in reflexive Banach spaces which have a weakly continuous duality mapping.
The iterative methods for nonexpansive mappings have recently been applied to solve convex minimization problems; see, for example, [12–14] and the references therein. Let  be a real Hilbert space, whose inner product and norm are denoted by
be a real Hilbert space, whose inner product and norm are denoted by  and
and  , respectively. Let
, respectively. Let  be a strongly positive bounded linear operator on
be a strongly positive bounded linear operator on  ; that is, there is a constant
; that is, there is a constant  with property
with property

A typical problem is to minimize a quadratic function over the set of the fixed points of a nonexpansive mapping on a real Hilbert space 

where  is a given point in
is a given point in  . In 2003, Xu [13] proved that the sequence
. In 2003, Xu [13] proved that the sequence  defined by the iterative method below, with the initial guess
defined by the iterative method below, with the initial guess  chosen arbitrarily
chosen arbitrarily

converges strongly to the unique solution of the minimization problem (1.5) provided the sequence  satisfies certain conditions. Using the viscosity approximation method, Moudafi [15] introduced the following iterative process for nonexpansive mappings (see [16] for further developments in both Hilbert and Banach spaces). Let
satisfies certain conditions. Using the viscosity approximation method, Moudafi [15] introduced the following iterative process for nonexpansive mappings (see [16] for further developments in both Hilbert and Banach spaces). Let  be a contraction on
be a contraction on  . Starting with an arbitrary initial
. Starting with an arbitrary initial  , define a sequence
, define a sequence  recursively by
recursively by

where  is a sequence in
is a sequence in  . It is proved [15, 16] that under certain appropriate conditions imposed on
. It is proved [15, 16] that under certain appropriate conditions imposed on  , the sequence
, the sequence  generated by (1.7) strongly converges to the unique solution
generated by (1.7) strongly converges to the unique solution  in
in  of the variational inequality
of the variational inequality

Recently, Marino and Xu [17] mixed the iterative method (1.6) and the viscosity approximation method (1.7) and considered the following general iterative method:

where  is a strongly positive bounded linear operator on
is a strongly positive bounded linear operator on  . They proved that if the sequence
. They proved that if the sequence  of parameters satisfies the following conditions:
of parameters satisfies the following conditions:
(C1) ,
,
(C2) ,
,
(C3) ,
,
then the sequence  generated by (1.9) converges strongly to the unique solution
generated by (1.9) converges strongly to the unique solution  in
in  of the variational inequality
of the variational inequality

which is the optimality condition for the minimization problem:  , where
, where  is a potential function for
is a potential function for  for
for  ).
).
On the other hand, in order to find a fixed point of nonexpansive mapping  , Halpern [18] was the first who introduced the following iteration scheme which was referred to as Halpern iteration in a Hilbert space:
, Halpern [18] was the first who introduced the following iteration scheme which was referred to as Halpern iteration in a Hilbert space:  ,
,

He pointed out that the control conditions (C1)  and (C2)
and (C2)  are necessary for the convergence of the iteration scheme (1.11) to a fixed point of
are necessary for the convergence of the iteration scheme (1.11) to a fixed point of  . Furthermore, the modified version of Halpern iteration was investigated widely by many mathematicians. Recently, for the sequence of nonexpansive mappings
. Furthermore, the modified version of Halpern iteration was investigated widely by many mathematicians. Recently, for the sequence of nonexpansive mappings  with some special conditions, Aoyama et al. [1] studied the strong convergence of the following modified version of Halpern iteration for
with some special conditions, Aoyama et al. [1] studied the strong convergence of the following modified version of Halpern iteration for  :
:

where  is a nonempty closed convex subset of a uniformly convex Banach space
is a nonempty closed convex subset of a uniformly convex Banach space  whose norm is uniformly Gáteaux differentiable,
whose norm is uniformly Gáteaux differentiable,  is a sequence in
is a sequence in  satisfying (C1)
satisfying (C1)  , (C2)
, (C2)  , and either (C3)
, and either (C3)  or (C3')
or (C3')  for all
for all  and
and  . Very recently, Song and Zheng [19] also introduced the conception of the condition
. Very recently, Song and Zheng [19] also introduced the conception of the condition  on a countable family of nonexpansive mappings and proved strong convergence theorems of the modified Halpern iteration (1.12) and the sequence
on a countable family of nonexpansive mappings and proved strong convergence theorems of the modified Halpern iteration (1.12) and the sequence  defined by
defined by

in a reflexive Banach space  with a weakly continuous duality mapping and in a reflexive strictly convex Banach space with a uniformly Gáteaux differentiable norm.
with a weakly continuous duality mapping and in a reflexive strictly convex Banach space with a uniformly Gáteaux differentiable norm.
Other investigations of approximating common fixed points for a countable family of nonexpansive mappings can be found in [1, 20–24] and many results not cited here.
In a Banach space  having a weakly continuous duality mapping
having a weakly continuous duality mapping  with a gauge function
with a gauge function  , an operator
, an operator  is said to be strongly positive [25] if there exists a constant
is said to be strongly positive [25] if there exists a constant  with the property
with the property


where  is the identity mapping. If
is the identity mapping. If  is a real Hilbert space, then the inequality (1.14) reduces to (1.4).
is a real Hilbert space, then the inequality (1.14) reduces to (1.4).
In this paper, motivated by Aoyama et al. [1], Song and Zheng [19], and Marino and Xu [17], we will combine the iterative method (1.12) with the viscosity approximation method (1.9) and consider the following three new general iterative methods in a reflexive Banach space  which admits a weakly continuous duality mapping
which admits a weakly continuous duality mapping  with gauge
with gauge  :
:


where  is strongly positive defined by (1.15),
is strongly positive defined by (1.15),  is a countable family of nonexpansive mappings, and
is a countable family of nonexpansive mappings, and  is an
is an  -contraction. We will prove in Section 3 that if the sequence
-contraction. We will prove in Section 3 that if the sequence  of parameters satisfies the appropriate conditions, then the sequences
of parameters satisfies the appropriate conditions, then the sequences  , and
, and  converge strongly to the unique solution
converge strongly to the unique solution  of the variational inequality
of the variational inequality

Finally, we apply our results to solve the the equilibrium problems and the problem of finding a zero of an accretive operator.
2. Preliminaries
Throughout this paper, let  be a real Banach space, and
be a real Banach space, and  be its dual space. We write
be its dual space. We write  (resp.,
(resp.,  ) to indicate that the sequence
) to indicate that the sequence  weakly (resp., weak*) converges to
weakly (resp., weak*) converges to  ; as usual
; as usual  will symbolize strong convergence. Let
will symbolize strong convergence. Let  . A Banach space
. A Banach space  is said to uniformly convex if, for any
is said to uniformly convex if, for any  , there exists
, there exists  such that, for any
such that, for any  ,
,  implies
implies  . It is known that a uniformly convex Banach space is reflexive and strictly convex (see also [26]). A Banach space
. It is known that a uniformly convex Banach space is reflexive and strictly convex (see also [26]). A Banach space  is said to be smooth if the limit
is said to be smooth if the limit  exists for all
exists for all  . It is also said to be uniformly smooth if the limit is attained uniformly for
. It is also said to be uniformly smooth if the limit is attained uniformly for  .
.
By a gauge function  , we mean a continuous strictly increasing function
, we mean a continuous strictly increasing function  such that
such that  and
and  as
as  . Let
. Let  be the dual space of
be the dual space of  . The duality mapping
. The duality mapping  associated to a gauge function
associated to a gauge function  is defined by
is defined by

In particular, the duality mapping with the gauge function  , denoted by
, denoted by  , is referred to as the normalized duality mapping. Clearly, there holds the relation
, is referred to as the normalized duality mapping. Clearly, there holds the relation  for all
for all  (see [27]). Browder [27] initiated the study of certain classes of nonlinear operators by means of the duality mapping
(see [27]). Browder [27] initiated the study of certain classes of nonlinear operators by means of the duality mapping  . Following Browder [27], we say that a Banach space
. Following Browder [27], we say that a Banach space  has a weakly continuous duality mapping if there exists a gauge
has a weakly continuous duality mapping if there exists a gauge  for which the duality mapping
for which the duality mapping  is single valued and continuous from the weak topology to the weak* topology, that is, for any
is single valued and continuous from the weak topology to the weak* topology, that is, for any  with
with  , the sequence
, the sequence  converges weakly* to
converges weakly* to  . It is known that
. It is known that  has a weakly continuous duality mapping with a gauge function
has a weakly continuous duality mapping with a gauge function  for all
for all  . Set
. Set

then

where  denotes the subdifferential in the sense of convex analysis.
denotes the subdifferential in the sense of convex analysis.
Now, we collect some useful lemmas for proving the convergence result of this paper.
The first part of the next lemma is an immediate consequence of the subdifferential inequality and the proof of the second part can be found in [28].
Lemma 2.1 (see [28]).
Assume that a Banach space  has a weakly continuous duality mapping
has a weakly continuous duality mapping  with gauge
with gauge  .
.
(i)For all  , the following inequality holds:
, the following inequality holds:

In particular, for all  ,
,

(ii)Assume that a sequence  in
in  converges weakly to a point
converges weakly to a point  ,
,
then the following identity holds:

Lemma 2.2 (see [1, Lemma 2.3]).
Let  be a sequence of nonnegative real numbers such that satisfying the property
be a sequence of nonnegative real numbers such that satisfying the property

where  satisfying the restrictions
satisfying the restrictions
(i) ; (ii)
; (ii) ; (iii)
; (iii) .
.
Then,  .
.
Definition 2.3 (see [1]).
Let  be a family of mappings from a subset
be a family of mappings from a subset  of a Banach space
of a Banach space  into
into  with
with  . We say that
. We say that  satisfies the AKTT-condition if for each bounded subset
satisfies the AKTT-condition if for each bounded subset  of
of  ,
,

Remark 2.4.
The example of the sequence of mappings  satisfying AKTT-condition is supported by Lemma 4.6.
satisfying AKTT-condition is supported by Lemma 4.6.
Lemma 2.5 (see [1, Lemma 3.2]).
Suppose that  satisfies AKTT-condition, then, for each
satisfies AKTT-condition, then, for each  ,
,  converses strongly to a point in
converses strongly to a point in  . Moreover, let the mapping
. Moreover, let the mapping  be defined by
be defined by

Then, for each bounded subset  of
of  ,
,  .
.
The next valuable lemma was proved by Wangkeeree et al. [25]. Here, we present the proof for the sake of completeness.
Lemma 2.6.
Assume that a Banach space  has a weakly continuous duality mapping
has a weakly continuous duality mapping  with gauge
with gauge  . Let
. Let  be a strongly positive bounded linear operator on
be a strongly positive bounded linear operator on  with coefficient
with coefficient  and
and  , then
, then  .
.
Proof.
From (1.15), we obtain that  . Now, for any
. Now, for any  with
with  , we see that
, we see that

That is,  is positive. It follows that
is positive. It follows that

Let  be a Banach space which admits a weakly continuous duality
be a Banach space which admits a weakly continuous duality  with gauge
with gauge  such that
such that  is invariant on
is invariant on  that is,
that is,  . Let
. Let  be a nonexpansive mapping,
be a nonexpansive mapping,  ,
,  an
an  -contraction, and
-contraction, and  a strongly positive bounded linear operator with coefficient
a strongly positive bounded linear operator with coefficient  and
and  . Define the mapping
. Define the mapping  by
by

Then,  is a contraction mapping. Indeed, for any
is a contraction mapping. Indeed, for any  ,
,

Thus, by Banach contraction mapping principle, there exists a unique fixed point  in
in  , that is
, that is

Remark 2.7.
We note that  space has a weakly continuous duality mapping with a gauge function
space has a weakly continuous duality mapping with a gauge function  for all
for all  . This shows that
. This shows that  is invariant on
is invariant on  .
.
Lemma 2.8 (see [25, Lemma 3.3]).
Let  be a reflexive Banach space which admits a weakly continuous duality mapping
be a reflexive Banach space which admits a weakly continuous duality mapping  with gauge
with gauge  such that
such that  is invariant on
is invariant on  . Let
. Let  be a nonexpansive mapping with
be a nonexpansive mapping with  ,
,  an
an  -contraction, and
-contraction, and  a strongly positive bounded linear operator with coefficient
a strongly positive bounded linear operator with coefficient  and
and  . Then, the net
. Then, the net  defined by (2.14) converges strongly as
defined by (2.14) converges strongly as  to a fixed point
to a fixed point  of
of  which solves the variational inequality
which solves the variational inequality

3. Main Results
We now state and prove the main theorems of this section.
Theorem 3.1.
Let  be a reflexive Banach space which admits a weakly continuous duality mapping
be a reflexive Banach space which admits a weakly continuous duality mapping  with gauge
with gauge  such that
such that  is invariant on
is invariant on  . Let
. Let  be a countable family of nonexpansive mappings satisfying
be a countable family of nonexpansive mappings satisfying  . Let
. Let  be an
be an  -contraction and
-contraction and  a strongly positive bounded linear operator with coefficient
a strongly positive bounded linear operator with coefficient  and
and  . Let the sequence
. Let the sequence  be generated by (1.16), where
be generated by (1.16), where  is a sequence in
is a sequence in  satisfying the following conditions:
satisfying the following conditions:
(C1) ,
,
(C2) ,
,
(C3) .
.
Suppose that  satisfies the AKTT-condition. Let
satisfies the AKTT-condition. Let  be a mapping of
be a mapping of  into itself defined by
into itself defined by  for all
for all  , and suppose that
, and suppose that  . Then,
. Then,  converges strongly to
converges strongly to  which solves the variational inequality
which solves the variational inequality

Proof.
Applying Lemma 2.8, there exists a point  which solves the variational inequality (3.1). Next, we observe that
which solves the variational inequality (3.1). Next, we observe that  is bounded. Indeed, pick any
is bounded. Indeed, pick any  to obtain
to obtain

It follows from induction that

Thus,  is bounded, and hence so are
is bounded, and hence so are  and
and  . Now, we show that
. Now, we show that

We observe that

for all  , where
, where  is a constant satisfying
is a constant satisfying  . Putting
. Putting  . From AKTT-condition and (C3), we have
. From AKTT-condition and (C3), we have

Therefore, it follows from Lemma 2.2 that  . Since
. Since  , we obtain
, we obtain

Using Lemma 2.5, we obtain

Next, we prove that

Let  be a subsequence of
be a subsequence of  such that
such that

If follows from reflexivity of  and the boundedness of a sequence
and the boundedness of a sequence  that there exists
that there exists  which is a subsequence of
which is a subsequence of  converging weakly to
converging weakly to  as
as  . Since
. Since  is weakly continuous, we have by Lemma 2.1 that
is weakly continuous, we have by Lemma 2.1 that

Let

It follows that

Then, from  , we have
, we have

On the other hand, however,

It follows from (3.14) and (3.15) that

Therefore,  , and hence
, and hence  . Since the duality map
. Since the duality map  is single valued and weakly continuous, we obtain, by (3.1), that
is single valued and weakly continuous, we obtain, by (3.1), that

Next, we show that  as
as  . In fact, since
. In fact, since  , and
, and  is a gauge function, then for
is a gauge function, then for  ,
,  and
and

Finally, we show that  as
as  . Following Lemma 2.1, we have
. Following Lemma 2.1, we have

It then follows that

where  . Put
. Put

It follows that from condition (C1),  and (3.9) that
and (3.9) that

Applying Lemma 2.2 to (3.20), we conclude that  as
as  ; that is,
; that is,  as
as  . This completes the proof.
. This completes the proof.
Setting  , where
, where  is the identity mapping and
is the identity mapping and  for all
for all  in Theorem 3.1, we have the following result.
in Theorem 3.1, we have the following result.
Corollary 3.2.
Let  be a reflexive Banach space which admits a weakly continuous duality mapping
be a reflexive Banach space which admits a weakly continuous duality mapping  with gauge
with gauge  . Suppose that
. Suppose that  is a countable family of nonexpansive mappings satisfying
is a countable family of nonexpansive mappings satisfying  . Assume that
. Assume that  is defined by, for
is defined by, for  ,
,

where  is a sequence in
is a sequence in  satisfying the following conditions:
satisfying the following conditions:
(C1) ,
,
(C2) ,
,
(C3) .
.
Suppose that  satisfies the AKTT-condition. Let
satisfies the AKTT-condition. Let  be a mapping of
be a mapping of  into itself defined by
into itself defined by  for all
for all  , and suppose that
, and suppose that  , then
, then  converges strongly to
converges strongly to  of
of  which solves the variational inequality
which solves the variational inequality

Applying Theorem 3.1, we can obtain the following two strong convergence theorems for the iterative sequences  and
and  defined by (1.17).
defined by (1.17).
Theorem 3.3.
Let  be a reflexive Banach space which admits a weakly continuous duality mapping
be a reflexive Banach space which admits a weakly continuous duality mapping  with gauge
with gauge  such that
such that  is invariant on
is invariant on  . Let
. Let  be a countable family of nonexpansive mappings satisfying
be a countable family of nonexpansive mappings satisfying  . Let
. Let  be an
be an  -contraction and
-contraction and  a strongly positive bounded linear operator with coefficient
a strongly positive bounded linear operator with coefficient  and
and  . Let the sequence
. Let the sequence  be generated by (1.17), where
be generated by (1.17), where  is a sequence in
is a sequence in  satisfying the following conditions:
satisfying the following conditions:
(C1) ,
,
(C2) ,
,
(C3) .
.
Suppose that  satisfies the AKTT-condition. Let
satisfies the AKTT-condition. Let  be a mapping of
be a mapping of  into itself defined by
into itself defined by  for all
for all  , and suppose that
, and suppose that  , then
, then  converges strongly to
converges strongly to  which solves the variational inequality (3.1).
which solves the variational inequality (3.1).
Proof.
Let  be the sequence given by
be the sequence given by  and
and

Form Theorem 3.1,  . We claim that
. We claim that  . Applying Lemma 2.6, we estimate
. Applying Lemma 2.6, we estimate

It follows from  ,
,  , and Lemma 2.2 that
, and Lemma 2.2 that  . Consequently,
. Consequently,  as required.
as required.
Theorem 3.4.
Let  be a reflexive Banach space which admits a weakly continuous duality mapping
be a reflexive Banach space which admits a weakly continuous duality mapping  with gauge
with gauge  such that
such that  is invariant on
is invariant on  . Let
. Let  be a countable family of nonexpansive mappings satisfying
be a countable family of nonexpansive mappings satisfying  . Let
. Let  be an
be an  -contraction and
-contraction and  a strongly positive bounded linear operator with coefficient
a strongly positive bounded linear operator with coefficient  and
and  . Let the sequence
. Let the sequence  be generated by (1.17), where
be generated by (1.17), where  is sequence in
is sequence in  satisfying the following conditions:
satisfying the following conditions:
(C1) ,
,
(C2) ,
,
(C3) .
.
Suppose that  satisfies the AKTT-condition. Let
satisfies the AKTT-condition. Let  be a mapping of
be a mapping of  into itself defined by
into itself defined by  for all
for all  , and suppose that
, and suppose that  , then
, then  converges strongly to
converges strongly to  which solves the variational inequality (3.1).
which solves the variational inequality (3.1).
Proof.
Let the sequences  and
and  be given by
be given by

Taking  , we have
, we have

It follows from induction that

Thus, both  and
and  are bounded. We observe that
are bounded. We observe that

Thus, Theorem 3.1 implies that  converges strongly to some point
converges strongly to some point  . In this case, we also have
. In this case, we also have

Hence, the sequence  converges strongly to
converges strongly to  . This competes the proof.
. This competes the proof.
Setting  , where
, where  is the identity mapping and
is the identity mapping and  for all
for all  in Theorem 3.4, we have the following result.
in Theorem 3.4, we have the following result.
Corollary 3.5.
Let  be a reflexive Banach space which admits a weakly continuous duality mapping
be a reflexive Banach space which admits a weakly continuous duality mapping  with gauge
with gauge  . Suppose that
. Suppose that  is a countable family of nonexpansive mappings satisfying
is a countable family of nonexpansive mappings satisfying  . Assume that
. Assume that  is defined by for
is defined by for  ,
,

where  is a sequence in
is a sequence in  satisfying the following conditions:
satisfying the following conditions:
(C1) ,
,
(C2) ,
,
(C3) .
.
Suppose that  satisfies the AKTT-condition. Let
satisfies the AKTT-condition. Let  be a mapping of
be a mapping of  into itself defined by
into itself defined by  for all
for all  , and suppose that
, and suppose that  , then
, then  converges strongly to
converges strongly to  of
of  which solves the variational inequality
which solves the variational inequality

4. Applications
4.1. 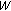 -Mappings
-Mappings
Let  be infinite mappings of
be infinite mappings of  into itself, and let
into itself, and let  be a nonnegative real sequence with
be a nonnegative real sequence with  ,
,  . For any
. For any  , define a mapping
, define a mapping  of
of  into itself as follows:
into itself as follows:

Nonexpansivity of each  ensures the nonexpansivity of
ensures the nonexpansivity of  . The mapping
. The mapping  is called a
is called a  -mapping generated by
-mapping generated by  and
and  .
.
Throughout this section, we will assume that  . Concerning
. Concerning  defined by (4.1), we have the following useful lemmas.
defined by (4.1), we have the following useful lemmas.
Lemma 4.1 (see [4]).
Let  be a nonempty closed convex subset of a a strictly convex, reflexive Banach space
be a nonempty closed convex subset of a a strictly convex, reflexive Banach space  ,
,  a family of infinitely nonexpansive mapping with
a family of infinitely nonexpansive mapping with  , and
, and  a real sequence such that
a real sequence such that  ,
,  , then:
, then:
(1) is nonexpansive and
is nonexpansive and  for each
for each  ;
;
(2)for each  and for each positive integer
and for each positive integer  , the limit
, the limit  exists;
exists;
(3)the mapping  define by
define by

is a nonexpansive mapping satisfying  , and it is called the
, and it is called the  -mapping generated by
-mapping generated by  and
and  .
.
From Remark 3.1 of Peng and Yao [29], we obtain the following lemma.
Lemma 4.2.
Let  be a strictly convex, reflexive Banach space,
be a strictly convex, reflexive Banach space,  a family of infinitely nonexpansive mappings with
a family of infinitely nonexpansive mappings with  , and
, and  a real sequence such that
a real sequence such that  ,
,  . Then sequence
. Then sequence  satisfies the
satisfies the  -condition.
-condition.
Applying Lemma 4.2 and Theorem 3.1, we obtain the following result.
Theorem 4.3.
Let  be a reflexive Banach space which admits a weakly continuous duality mapping
be a reflexive Banach space which admits a weakly continuous duality mapping  with gauge
with gauge  such that
such that  is invariant on
is invariant on  . Let
. Let  be a countable family of nonexpansive mappings with
be a countable family of nonexpansive mappings with  and
and  an
an  -contraction and
-contraction and  a strongly positive bounded linear operator with coefficient
a strongly positive bounded linear operator with coefficient  and
and  . Let the sequence
. Let the sequence  be generated by the following:
be generated by the following:

where  is defined by (4.1) and
is defined by (4.1) and  is a sequence in
is a sequence in  satisfying the conditions (C1), (C2), and (C3). Then
satisfying the conditions (C1), (C2), and (C3). Then  converges strongly to
converges strongly to  in
in  .
.
Applying Lemma 4.2 and Theorem 3.3, we obtain the following result.
Theorem 4.4.
Let  ,
,  ,
,  ,
,  ,
,  , and
, and  be as in Theorem 4.3. Let the sequence
be as in Theorem 4.3. Let the sequence  be generated by the following:
be generated by the following:

then  converges strongly to
converges strongly to  in
in  .
.
Applying Lemma 4.2 and Theorem 3.4, we obtain the following result.
Theorem 4.5.
Let  ,
,  ,
,  ,
,  ,
,  , and
, and  be as in Theorem 4.3. Let the sequence
be as in Theorem 4.3. Let the sequence  be generated by the following:
be generated by the following:

then  converges strongly to
converges strongly to  in
in  .
.
4.2. Accretive Operators
We consider the problem of finding a zero of an accretive operator. An operator  is said to be accretive if for each
is said to be accretive if for each  and
and  , there exists
, there exists  such that
such that  . An accretive operator
. An accretive operator  is said to satisfy the range condition if
is said to satisfy the range condition if  for all
for all  , where
, where  is the domain of
is the domain of  ,
,  is the identity mapping on
is the identity mapping on  ,
,  is the range of
is the range of  , and
, and  is the closure of
is the closure of  . If
. If  is an accretive operator which satisfies the range condition, then we can define, for each
is an accretive operator which satisfies the range condition, then we can define, for each  , a mapping
, a mapping  by
by  , which is called the resolvent of
, which is called the resolvent of  . We know that
. We know that  is nonexpansive and
is nonexpansive and  for all
for all  . We also know the following [30]: for each
. We also know the following [30]: for each  and
and  , it holds that
, it holds that

From the Resolvent identity, we have the following lemma.
Lemma 4.6.
Let  be a Banach space and
be a Banach space and  a nonempty closed convex subset of
a nonempty closed convex subset of  . Let
. Let  be an accretive operator such that
be an accretive operator such that  and
and  . Suppose that
. Suppose that  is a sequence of
is a sequence of  such that
such that  and
and  , then
, then
(i)the sequence  satisfies AKTT-condition,
satisfies AKTT-condition,
(ii) for all
for all  and
and  , where
, where  as
as  .
.
Proof.
By the proof of Theorem 4.3 in [1] and applying Lemma 4.6 and Theorem 3.1, we obtain the following result.
Theorem 4.7.
Let  be a reflexive Banach space which admits a weakly continuous duality mapping
be a reflexive Banach space which admits a weakly continuous duality mapping  with gauge
with gauge  such that
such that  is invariant on
is invariant on  . Let
. Let  be an accretive operator such that
be an accretive operator such that  . Assume that
. Assume that  is a nonempty closed convex subset of
is a nonempty closed convex subset of  such that
such that  and
and  is an
is an  -contraction. Let
-contraction. Let  be a strongly positive bounded linear operator with coefficient
be a strongly positive bounded linear operator with coefficient  and
and  . Suppose that
. Suppose that  is a sequence of
is a sequence of  such that
such that  . Let the sequence
. Let the sequence  be generated by the following:
be generated by the following:

where  is a sequence in
is a sequence in  satisfying the following conditions (C1), (C2), and (C3), then
satisfying the following conditions (C1), (C2), and (C3), then  converges strongly to
converges strongly to  in
in  .
.
Applying Lemma 4.6 and Theorem 3.3, we obtain the following result.
Theorem 4.8.
Let  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  be as in Theorem 4.7. Let
be as in Theorem 4.7. Let  be generated by the following:
be generated by the following:

then  converges strongly to
converges strongly to  in
in  .
.
Applying Lemma 4.6 and Theorem 3.4, we obtain the following result.
Theorem 4.9.
Let  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  be as in Theorem 4.7. Let
be as in Theorem 4.7. Let  be generated by the following:
be generated by the following:

Then  converges strongly to
converges strongly to  in
in  .
.
4.3. The Equilibrium Problems
Let  be a real Hilbert space, and let
be a real Hilbert space, and let  be a bifunction of
be a bifunction of  , where
, where  is the set of real numbers. The equilibrium problem for
is the set of real numbers. The equilibrium problem for  is to find
is to find  such that
such that

The set of solutions of (4.10) is denoted by  . Given a mapping
. Given a mapping  , let
, let  for all
for all  . Then,
. Then,  if and only if
if and only if  for all
for all  , that is,
, that is,  is a solution of the variational inequality. Numerous problems in physics, optimization, and economics reduce to find a solution of (4.10). Some methods have been proposed to solve the equilibrium problem; see, for instance, Blum and Oettli [31] and Combettes and Hirstoaga [32]. For the purpose of solving the equilibrium problem for a bifunction
is a solution of the variational inequality. Numerous problems in physics, optimization, and economics reduce to find a solution of (4.10). Some methods have been proposed to solve the equilibrium problem; see, for instance, Blum and Oettli [31] and Combettes and Hirstoaga [32]. For the purpose of solving the equilibrium problem for a bifunction  , let us assume that
, let us assume that  satisfies the following conditions:
satisfies the following conditions:
(A1) for all
for all  ,
,
(A2) is monotone, that is,
is monotone, that is,  for all
for all  ,
,
(A3) for each  ,
,
(A4) for each  is convex and lower semicontinuous.
is convex and lower semicontinuous.
The following lemmas were also given in [31, 32], respectively.
Lemma 4.10 (see [31, Corollary 1]).
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and let
, and let  be a bifunction of
be a bifunction of  satisfying
satisfying  . Let
. Let  and
and  , then there exists
, then there exists  such that
such that  .
.
Lemma 4.11 (see [32, Lemma 2.12]).
Assume that  satisfies
satisfies  . For
. For  and
and  , define a mapping
, define a mapping  as follows:
as follows:

then, the following hold:
(1) is single valued,
is single valued,
(2) is firmly nonexpansive, that is, for any
is firmly nonexpansive, that is, for any  ,
,
(3) ,
,
(4) is closed and convex.
is closed and convex.
Theorem 4.12.
Let  be a real Hilbert space. Let
be a real Hilbert space. Let  be a bifunction from
be a bifunction from  satisfying (A1)–(A4) and
satisfying (A1)–(A4) and  . Let
. Let  be an
be an  -contraction,
-contraction,  a strongly positive bounded linear operator with coefficient
a strongly positive bounded linear operator with coefficient  and
and  . Let the sequences
. Let the sequences  be generated by
be generated by  and
and

for all  , where
, where  is a sequence in
is a sequence in  and
and  satisfying the following conditions:
satisfying the following conditions:
(C1) ,
,
(C2) ,
,
(C3) ,
,
(C4) and
and  .
.
then  and
and  converge strongly to
converge strongly to  .
.
Proof.
Following the proof technique of Theorem 3.1, we only need, show that  , for all
, for all  . From (4.12), it follows that
. From (4.12), it follows that

On the other hand, from the definition of  we have
we have

Putting  and
and  in (4.14), we have
in (4.14), we have

So, from (A2), we have

and hence,

then we have

and hence,

where  is a constant satisfying
is a constant satisfying  . Substituting (4.19) in (4.13) yields
. Substituting (4.19) in (4.13) yields

for some  with
with  (the definition
(the definition  ). By the assumptions on
). By the assumptions on  and
and  and using Lemma 2.2, we conclude that
and using Lemma 2.2, we conclude that

From the definition of  and
and  , it follows that
, it follows that

Combining (4.21) and (4.22), we have

From the definition of  , it follows that
, it follows that

Putting  in (4.14) and
in (4.14) and  in (4.24), we have
in (4.24), we have

So, from (A2), we have

and hence, for each  ,
,

then

Since

then for each  , we have from (4.23)
, we have from (4.23)

This completes the proof.
Applying Theorem 4.12, we can obtain the following result.
Corollary 4.13.
Let  be a real Hilbert space. Let
be a real Hilbert space. Let  be a bifunction from
be a bifunction from  satisfying (A1)–(A4) and
satisfying (A1)–(A4) and  . Let
. Let  be an
be an  -contraction,
-contraction,  a strongly positive bounded linear operator with coefficient
a strongly positive bounded linear operator with coefficient  and
and  . Let the sequences
. Let the sequences  be generated by
be generated by  and
and

for all  , where
, where  is a sequence in
is a sequence in  and
and  satisfying the following conditions:
satisfying the following conditions:
(C1) ,
,
(C2) ,
,
(C3) ,
,
(C4) and
and  ,
,
then  and
and  converge strongly to
converge strongly to  .
.
Proof.
We observe that  for all
for all  . Then we rewrite the iterative sequence (4.31) by the following:
. Then we rewrite the iterative sequence (4.31) by the following:

Let  be the sequence given by
be the sequence given by  and
and

Form Theorem 4.12,  in
in  . We claim that
. We claim that  . Applying Lemma 2.6, we estimate
. Applying Lemma 2.6, we estimate

It follows from  ,
,  , and Lemma 2.2 that
, and Lemma 2.2 that  as
as  . Consequently,
. Consequently,  as required.
as required.
References
Aoyama K, Kimura Y, Takahashi W, Toyoda M: Approximation of common fixed points of a countable family of nonexpansive mappings in a Banach space. Nonlinear Analysis: Theory, Methods & Applications 2007,67(8):2350–2360. 10.1016/j.na.2006.08.032
Bauschke HH: The approximation of fixed points of compositions of nonexpansive mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1996,202(1):150–159. 10.1006/jmaa.1996.0308
Shang M, Su Y, Qin X: Strong convergence theorems for a finite family of nonexpansive mappings. Fixed Point Theory and Applications 2007, 2007:-9.
Shimoji K, Takahashi W: Strong convergence to common fixed points of infinite nonexpansive mappings and applications. Taiwanese Journal of Mathematics 2001,5(2):387–404.
Bauschke HH, Borwein JM: On projection algorithms for solving convex feasibility problems. SIAM Review 1996,38(3):367–426. 10.1137/S0036144593251710
Combettes PL: Foundations of set theoretic estimation. Proceedings of the IEEE 1993,81(2):182–208.
Youla DC: Mathematical theory of image restoration by the method of convex projections. In Image Recovery: Theory and Applications. Edited by: Stark H. Academic Press, Orlando, Fla, USA; 1987:29–77.
Iusem AN, De Pierro AR: On the convergence of Han's method for convex programming with quadratic objective. Mathematical Programming. Series B 1991,52(2):265–284.
Browder FE: Fixed-point theorems for noncompact mappings in Hilbert space. Proceedings of the National Academy of Sciences of the United States of America 1965, 53: 1272–1276. 10.1073/pnas.53.6.1272
Reich S: Strong convergence theorems for resolvents of accretive operators in Banach spaces. Journal of Mathematical Analysis and Applications 1980,75(1):287–292. 10.1016/0022-247X(80)90323-6
Xu H-K: Strong convergence of an iterative method for nonexpansive and accretive operators. Journal of Mathematical Analysis and Applications 2006,314(2):631–643. 10.1016/j.jmaa.2005.04.082
Deutsch F, Yamada I: Minimizing certain convex functions over the intersection of the fixed point sets of nonexpansive mappings. Numerical Functional Analysis and Optimization 1998,19(1–2):33–56.
Xu H-K: An iterative approach to quadratic optimization. Journal of Optimization Theory and Applications 2003,116(3):659–678. 10.1023/A:1023073621589
Xu H-K: Iterative algorithms for nonlinear operators. Journal of the London Mathematical Society. Second Series 2002,66(1):240–256. 10.1112/S0024610702003332
Moudafi A: Viscosity approximation methods for fixed-points problems. Journal of Mathematical Analysis and Applications 2000,241(1):46–55. 10.1006/jmaa.1999.6615
Xu H-K: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004,298(1):279–291. 10.1016/j.jmaa.2004.04.059
Marino G, Xu H-K: A general iterative method for nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2006,318(1):43–52. 10.1016/j.jmaa.2005.05.028
Halpern B: Fixed points of nonexpanding maps. Bulletin of the American Mathematical Society 1967, 73: 957–961. 10.1090/S0002-9904-1967-11864-0
Song Y, Zheng Y: Strong convergence of iteration algorithms for a countable family of nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 2009,71(7–8):3072–3082. 10.1016/j.na.2009.01.219
Jung JS: Iterative approaches to common fixed points of nonexpansive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 2005,302(2):509–520. 10.1016/j.jmaa.2004.08.022
O'Hara JG, Pillay P, Xu H-K: Iterative approaches to finding nearest common fixed points of nonexpansive mappings in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 2003,54(8):1417–1426. 10.1016/S0362-546X(03)00193-7
O'Hara JG, Pillay P, Xu H-K: Iterative approaches to convex feasibility problems in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2006,64(9):2022–2042. 10.1016/j.na.2005.07.036
Wangkeeree R: An extragradient approximation method for equilibrium problems and fixed point problems of a countable family of nonexpansive mappings. Fixed Point Theory and Applications 2008, 2008:-17.
Wangkeeree R, Kamraksa U: A general iterative method for solving the variational inequality problem and fixed point problem of an infinite family of nonexpansive mappings in Hilbert spaces. Fixed Point Theory and Applications 2009, 2009:-23.
Wangkeeree R, Petrot N, Wangkeeree R: The general iterative methods for nonexpansive mappings in Banach spaces. Journal of Global Optimization. In press
Takahashi W: Nonlinear Functional Analysis: Fixed Point Theory and Its Applications. Yokohama Publishers, Yokohama, Japan; 2000:iv+276.
Browder FE: Convergence theorems for sequences of nonlinear operators in Banach spaces. Mathematische Zeitschrift 1967, 100: 201–225. 10.1007/BF01109805
Lim T-C, Xu H-K: Fixed point theorems for asymptotically nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 1994,22(11):1345–1355. 10.1016/0362-546X(94)90116-3
Peng J-W, Yao J-C: A viscosity approximation scheme for system of equilibrium problems, nonexpansive mappings and monotone mappings. Nonlinear Analysis: Theory, Methods & Applications 2009,71(12):6001–6010. 10.1016/j.na.2009.05.028
Eshita K, Takahashi W: Approximating zero points of accretive operators in general Banach spaces. JP Journal of Fixed Point Theory and Applications 2007,2(2):105–116.
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994,63(1–4):123–145.
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. Journal of Nonlinear and Convex Analysis 2005,6(1):117–136.
Acknowledgments
The authors would like to thank the Centre of Excellence in Mathematics, Thailand for financial support. Finally, They would like to thank the referees for reading this paper carefully, providing valuable suggestions and comments, and pointing out a major error in the original version of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Nammanee, K., Wangkeeree, R. New Iterative Approximation Methods for a Countable Family of Nonexpansive Mappings in Banach Spaces. Fixed Point Theory Appl 2011, 671754 (2011). https://doi.org/10.1155/2011/671754
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/671754
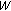 -Mappings
-Mappings