- Research Article
- Open access
- Published:
Fixed-Point Results for Generalized Contractions on Ordered Gauge Spaces with Applications
Fixed Point Theory and Applications volume 2011, Article number: 979586 (2011)
Abstract
The purpose of this paper is to present some fixed-point results for single-valued  -contractions on ordered and complete gauge space. Our theorems generalize and extend some recent results in the literature. As an application, existence results for some integral equations on the positive real axis are given.
-contractions on ordered and complete gauge space. Our theorems generalize and extend some recent results in the literature. As an application, existence results for some integral equations on the positive real axis are given.
1. Introduction
Throughout this paper  will denote a nonempty set
will denote a nonempty set  endowed with a separating gauge structure
endowed with a separating gauge structure 
 , where
, where  is a directed set (see [1] for definitions). Let
is a directed set (see [1] for definitions). Let  and
and  . We also denote by
. We also denote by  the set of all real numbers and by
the set of all real numbers and by  .
.
A sequence  of elements in
of elements in  is said to be Cauchy if for every
is said to be Cauchy if for every  and
and  , there is an
, there is an  with
with  for all
for all  and
and  . The sequence
. The sequence  is called convergent if there exists an
is called convergent if there exists an  such that for every
such that for every  and
and  , there is an
, there is an  with
with  , for all
, for all  .
.
A gauge space  is called complete if any Cauchy sequence is convergent. A subset of
is called complete if any Cauchy sequence is convergent. A subset of  is said to be closed if it contains the limit of any convergent sequence of its elements. See also Dugundji [1] for other definitions and details.
is said to be closed if it contains the limit of any convergent sequence of its elements. See also Dugundji [1] for other definitions and details.
If  is an operator, then
is an operator, then  is called fixed point for
is called fixed point for  if and only if
if and only if  . The set
. The set  denotes the fixed-point set of
denotes the fixed-point set of  .
.
On the other hand, Ran and Reurings [2] proved the following Banach-Caccioppoli type principle in ordered metric spaces.
Theorem 1.1 (Ran and Reurings [2]).
Let  be a partially ordered set such that every pair
be a partially ordered set such that every pair  has a lower and an upper bound. Let
has a lower and an upper bound. Let  be a metric on
be a metric on  such that the metric space
such that the metric space  is complete. Let
is complete. Let  be a continuous and monotone (i.e., either decreasing or increasing) operator. Suppose that the following two assertions hold:
be a continuous and monotone (i.e., either decreasing or increasing) operator. Suppose that the following two assertions hold:
(1)there exists  such that
such that  , for each
, for each  with
with  ;
;
(2)there exists  such that
such that  or
or  .
.
Then  has an unique fixed point
has an unique fixed point  , that is,
, that is,  , and for each
, and for each  the sequence
the sequence  of successive approximations of
of successive approximations of  starting from
starting from  converges to
converges to  .
.
Since then, several authors considered the problem of existence (and uniqueness) of a fixed point for contraction-type operators on partially ordered sets.
In 2005, Nieto and Rodrguez-López proved a modified variant of Theorem 1.1, by removing the continuity of  . The case of decreasing operators is treated in Nieto and Rodrguez-López [3], where some interesting applications to ordinary differential equations with periodic boundary conditions are also given. Nieto, Pouso, and Rodrguez-López, in a very recent paper, improve some results given by Petruşel and Rus in [4] in the setting of abstract
. The case of decreasing operators is treated in Nieto and Rodrguez-López [3], where some interesting applications to ordinary differential equations with periodic boundary conditions are also given. Nieto, Pouso, and Rodrguez-López, in a very recent paper, improve some results given by Petruşel and Rus in [4] in the setting of abstract  -spaces in the sense of Fréchet, see, for example, [5, Theorems 3.3 and 3.5]. Another fixed-point result of this type was given by O'Regan and Petruşel in [6] for the case of
-spaces in the sense of Fréchet, see, for example, [5, Theorems 3.3 and 3.5]. Another fixed-point result of this type was given by O'Regan and Petruşel in [6] for the case of  -contractions in ordered complete metric spaces.
-contractions in ordered complete metric spaces.
The aim of this paper is to present some fixed-point theorems for  -contractions on ordered and complete gauge space. As an application, existence results for some integral equations on the positive real axis are given. Our theorems generalize the above-mentioned theorems as well as some other ones in the recent literature (see; Ran and Reurings [2], Nieto and Rodrguez-López [3, 7], Nieto et al. [5], Petruşel and Rus [4], Agarwal et al. [8], O'Regan and Petruşel [6], etc.).
-contractions on ordered and complete gauge space. As an application, existence results for some integral equations on the positive real axis are given. Our theorems generalize the above-mentioned theorems as well as some other ones in the recent literature (see; Ran and Reurings [2], Nieto and Rodrguez-López [3, 7], Nieto et al. [5], Petruşel and Rus [4], Agarwal et al. [8], O'Regan and Petruşel [6], etc.).
2. Preliminaries
Let  be a nonempty set and
be a nonempty set and  be an operator. Then,
be an operator. Then,  ,
,  ,
,  denote the iterate operators of
denote the iterate operators of  . Let
. Let  be a nonempty set and let
be a nonempty set and let  . Let
. Let  a subset of
a subset of  and
and  an operator. By definition the triple
an operator. By definition the triple  is called an
is called an  -space (Fréchet [9]) if the following conditions are satisfied.
-space (Fréchet [9]) if the following conditions are satisfied.
(i)If  , for all
, for all  , then
, then  and
and  .
.
(ii)If  and
and  , then for all subsequences,
, then for all subsequences,  , of
, of  we have that
we have that  and
and  .
.
By definition, an element of  is a convergent sequence,
is a convergent sequence,  is the limit of this sequence and we also write
is the limit of this sequence and we also write  .
.
In what follow we denote an  -space by
-space by  .
.
In this setting, if  , then an operator
, then an operator  is called orbitally
is called orbitally  -continuous (see [5]) if [
-continuous (see [5]) if [ and
and  , as
, as  and
and  for any
for any  ] imply [
] imply [ , as
, as  ]. In particular, if
]. In particular, if  , then
, then  is called orbitally continuous.
is called orbitally continuous.
Let  be a partially ordered set, that is,
be a partially ordered set, that is,  is a nonempty set and ≤ is a reflexive, transitive, and antisymmetric relation on
is a nonempty set and ≤ is a reflexive, transitive, and antisymmetric relation on  . Denote
. Denote

Also, if  , with
, with  then by
then by  we will denote the ordered segment joining
we will denote the ordered segment joining  and
and  , that is,
, that is,  . In the same setting, consider
. In the same setting, consider  . Then,
. Then,  is the lower fixed-point set of
is the lower fixed-point set of  , while
, while  is the upper fixed-point set of
is the upper fixed-point set of  . Also, if
. Also, if  and
and  , then the cartesian product of
, then the cartesian product of  and
and  is denoted by
is denoted by  , and it is defined in the following way:
, and it is defined in the following way:  ,
,  .
.
Definition 2.1.
Let  be a nonempty set. By definition
be a nonempty set. By definition  is an ordered
is an ordered  -space if and only if
-space if and only if
(i) is an
is an  -space;
-space;
(ii) is a partially ordered set;
is a partially ordered set;
(iii) ,
,  and
and  , for each
, for each  .
.
If  is a gauge space, then the convergence structure is given by the family of gauges
is a gauge space, then the convergence structure is given by the family of gauges 
 . Hence,
. Hence,  is an ordered
is an ordered  -space, and it will be called an ordered gauge space, see also [10, 11].
-space, and it will be called an ordered gauge space, see also [10, 11].
Recall that  is said to be a comparison function if it is increasing and
is said to be a comparison function if it is increasing and  , as
, as  . As a consequence, we also have
. As a consequence, we also have  , for each
, for each  ,
,  and
and  is right continuous at 0. For example,
is right continuous at 0. For example,  (where
(where  ),
),  and
and  ,
,  are comparison functions.
are comparison functions.
Recall now the following important abstract concept.
Definition 2.2 (Rus [12]).
Let  be an
be an  -space. An operator
-space. An operator  is, by definition, a Picard operator if
is, by definition, a Picard operator if
(i) ;
;
(ii) as
as  , for all
, for all  .
.
Several classical results in fixed-point theory can be easily transcribed in terms of the Picard operators, see [4, 13, 14]. In Rus [12] the basic theory of Picard operators is presented.
3. Fixed-Point Results
Our first main result is the following existence, uniqueness, and approximation fixed-point theorem.
Theorem 3.1.
Let  be an ordered complete gauge space and
be an ordered complete gauge space and  be an operator. Suppose that
be an operator. Suppose that
(i)for each  with
with  there exists
there exists  such that
such that  and
and  ;
;
(ii) ;
;
(iii)if  and
and  , then
, then  ;
;
(iv)there exists  such that
such that  ;
;
(v) is orbitally continuous;
is orbitally continuous;
(vi)there exists a comparison function  such that, for each
such that, for each  one has
one has

Then,  is a Picard operator.
is a Picard operator.
Proof.
Let  be such that
be such that  . Suppose first that
. Suppose first that  . Then, from (ii) we obtain
. Then, from (ii) we obtain

From (vi), by induction, we get, for each  , that
, that

Since  as
as  , for an arbitrary
, for an arbitrary  we can choose
we can choose  such that
such that  , for each
, for each  . Since
. Since  for all
for all  , we have for all
, we have for all  that
that

Now since  (see (iii)) we have for any
(see (iii)) we have for any  that
that

By induction, for each  , we have
, we have

Hence  is a Cauchy sequence in
is a Cauchy sequence in  . From the completeness of the gauge space we have
. From the completeness of the gauge space we have  , as
, as  .
.
Let  be arbitrarily chosen. Then;
be arbitrarily chosen. Then;
(1)If  then
then  and thus, for each
and thus, for each  , we have
, we have  , for each
, for each  . Letting
. Letting  we obtain that
we obtain that  .
.
(2)If  then, by (i), there exists
then, by (i), there exists  such that
such that  and
and  . From the second relation, as before, we get, for each
. From the second relation, as before, we get, for each  , that
, that  , for each
, for each  and hence
and hence  , as
, as  . Then, using the first relation we infer that, for each
. Then, using the first relation we infer that, for each  , we have
, we have  , for each
, for each  . Letting again
. Letting again  , we conclude
, we conclude  .
.
By the orbital continuity of  we get that
we get that  . Thus
. Thus  . If we have
. If we have  for some
for some  , then from above, we must have
, then from above, we must have  , so
, so  .
.
If  , then
, then  plays the role of
plays the role of  .
.
Remark 3.2.
Equivalent representation of condition (iv) are as follows.
(iv)'There exists  such that
such that  or
or 
(iv)" .
.
Remark 3.3.
Condition (ii) can be replaced by each of the following assertions:
(ii)' is increasing,
is increasing,
(ii)" is decreasing.
is decreasing.
However, it is easy to see that assertion (ii) in Theorem 3.1. is more general.
As a consequence of Theorem 3.1, we have the following result very useful for applications.
Theorem 3.4.
Let  be an ordered complete gauge space and
be an ordered complete gauge space and  be an operator. One supposes that
be an operator. One supposes that
(i)for each  with
with  there exists
there exists  such that
such that  and
and  ;
;
(ii) is increasing;
is increasing;
(iii)there exists  such that
such that  ;
;
(iv)
(a) is orbitally continuous or
is orbitally continuous or
(b)if an increasing sequence  converges to
converges to  in
in  , then
, then  for all
for all  ;
;
(v)there exists a comparison function  such that
such that

(vi)if  and
and  , then
, then 
Then  is a Picard operator.
is a Picard operator.
Proof.
Since  is increasing and
is increasing and  we immediately have
we immediately have  . Hence from (v) we obtain
. Hence from (v) we obtain  , for each
, for each  . By a similar approach as in the proof of Theorem 3.1 we obtain
. By a similar approach as in the proof of Theorem 3.1 we obtain

Hence  is a Cauchy sequence in
is a Cauchy sequence in  . From the completeness of the gauge space we have that
. From the completeness of the gauge space we have that  as
as  .
.
By the orbital continuity of the operator  we get that
we get that  . If (iv)(b) takes place, then, since
. If (iv)(b) takes place, then, since  , given any
, given any  there exists
there exists  such that for each
such that for each  we have
we have  . On the other hand, for each
. On the other hand, for each  , since
, since  , we have, for each
, we have, for each  that
that

Thus  .
.
The uniqueness of the fixed point follows by contradiction. Suppose there exists  , with
, with  . There are two possible cases.
. There are two possible cases.
(a)If  , then we have
, then we have  as
as  , which is a contradiction. Hence
, which is a contradiction. Hence  .
.
(b)If  then there exists
then there exists  such that
such that  and
and  . The monotonicity condition implies that
. The monotonicity condition implies that  and
and  are comparable as well as
are comparable as well as  and
and  . Hence
. Hence 
 ,
,  as
as  , which is again a contradiction. Thus
, which is again a contradiction. Thus  .
.
4. Applications
We will apply the above result to nonlinear integral equations on the real axis

Theorem 4.1.
Consider (4.1). Suppose that
(i) and
and  are continuous;
are continuous;
(ii) is increasing for each
is increasing for each  ;
;
(iii)there exists a comparison function  , with
, with  for each
for each  and any
and any  , such that
, such that

(iv)there exists  such that
such that

Then the integral equation (4.1) has a unique solution  in
in  .
.
Proof.
Let  and the family of pseudonorms
and the family of pseudonorms

Define now  for
for  .
.
Then  is family of gauges on
is family of gauges on  . Consider on
. Consider on  the partial order defined by
the partial order defined by

Then  is an ordered and complete gauge space. Moreover, for any increasing sequence
is an ordered and complete gauge space. Moreover, for any increasing sequence  in
in  converging to some
converging to some  we have
we have  , for any
, for any  . Also, for every
. Also, for every  there exists
there exists  which is comparable to
which is comparable to  and
and  .
.
Define  , by the formula
, by the formula

First observe that from (ii)  is increasing. Also, for each
is increasing. Also, for each  with
with  and for
and for  , we have
, we have

Hence, for  we obtain
we obtain

From (iv) we have that  . The conclusion follows now from Theorem 3.4.
. The conclusion follows now from Theorem 3.4.
Consider now the following equation:

Theorem 4.2.
Consider (4.9). Suppose that
(i) and
and  are continuous;
are continuous;
(ii) is increasing for each
is increasing for each  ;
;
(iii)there exists a comparison function  , with
, with  for each
for each  and any
and any  , such that
, such that

(iv)there exists  such that
such that

Then the integral equation (4.9) has a unique solution  in
in  .
.
Proof.
We consider the gauge space  where
where

and the operator  defined by
defined by

As before, consider on  the partial order defined by
the partial order defined by

Then  is an ordered and complete gauge space. Moreover, for any increasing sequence
is an ordered and complete gauge space. Moreover, for any increasing sequence  in
in  converging to a certain
converging to a certain  we have
we have  , for any
, for any  . Also, for every
. Also, for every  there exists
there exists  which is comparable to
which is comparable to  and
and  . Notice that (ii) implies that
. Notice that (ii) implies that  is increasing.
is increasing.
From condition (iii), for  with
with  , we have
, we have

Thus, for any  , we obtain
, we obtain

As before, from (iv) we have that  . The conclusion follows again by Theorem 3.4.
. The conclusion follows again by Theorem 3.4.
Remark 4.3.
It is worth mentioning that it could be of interest to extend the above technique for other metrical fixed-point theorems, see [15, 16], and so forth.
References
Dugundji J: Topology. Allyn and Bacon, Boston, Mass, USA; 1966:xvi+447.
Ran ACM, Reurings MCB: A fixed point theorem in partially ordered sets and some applications to matrix equations. Proceedings of the American Mathematical Society 2004,132(5):1435–1443. 10.1090/S0002-9939-03-07220-4
Nieto JJ, Rodríguez-López R: Existence and uniqueness of fixed point in partially ordered sets and applications to ordinary differential equations. Acta Mathematica Sinica 2007,23(12):2205–2212. 10.1007/s10114-005-0769-0
Petruşel A, Rus IA: Fixed point theorems in ordered
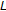 -spaces. Proceedings of the American Mathematical Society 2006,134(2):411–418.
-spaces. Proceedings of the American Mathematical Society 2006,134(2):411–418.Nieto JJ, Pouso RL, Rodríguez-López R: Fixed point theorems in ordered abstract spaces. Proceedings of the American Mathematical Society 2007,135(8):2505–2517. 10.1090/S0002-9939-07-08729-1
O'Regan D, Petruşel A: Fixed point theorems for generalized contractions in ordered metric spaces. Journal of Mathematical Analysis and Applications 2008,341(2):1241–1252. 10.1016/j.jmaa.2007.11.026
Nieto JJ, Rodríguez-López R: Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations. Order 2005,22(3):223–239. 10.1007/s11083-005-9018-5
Agarwal RP, El-Gebeily MA, O'Regan D: Generalized contractions in partially ordered metric spaces. Applicable Analysis 2008,87(1):109–116. 10.1080/00036810701556151
Fréchet M: Les Espaces Abstraits. Gauthier-Villars, Paris, France; 1928.
Petruşel G: Fixed point results for multivalued contractions on ordered gauge spaces. Central European Journal of Mathematics 2009,7(3):520–528. 10.2478/s11533-009-0027-2
Petruşel G, Luca I: Strict fixed point results for multivalued contractions on gauge spaces. Fixed Point Theory 2010,11(1):119–124.
Rus IA: Picard operators and applications. Scientiae Mathematicae Japonicae 2003,58(1):191–219.
Rus IA: The theory of a metrical fixed point theoremml: theoretical and applicative relevances. Fixed Point Theory 2008,9(2):541–559.
Rus IA, Petruşel A, Petruşel G: Fixed Point Theory. Cluj University Press, Cluj-Napoca, Romania; 2008.
Caballero J, Harjani J, Sadarangani K: Contractive-like mapping principles in ordered metric spaces and application to ordinary differential equations. Fixed Point Theory and Applications 2010, 2010:-14.
Harjani J, Sadarangani K: Fixed point theorems for weakly contractive mappings in partially ordered sets. Nonlinear Analysis. Theory, Methods & Applications 2009,71(7–8):3403–3410. 10.1016/j.na.2009.01.240
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chifu, C., Petruşel, G. Fixed-Point Results for Generalized Contractions on Ordered Gauge Spaces with Applications. Fixed Point Theory Appl 2011, 979586 (2011). https://doi.org/10.1155/2011/979586
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/979586
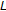 -spaces. Proceedings of the American Mathematical Society 2006,134(2):411–418.
-spaces. Proceedings of the American Mathematical Society 2006,134(2):411–418.