- Research Article
- Open access
- Published:
Common fixed point and invariant approximation results in certain metrizable topological vector spaces
Fixed Point Theory and Applications volume 2006, Article number: 23582 (2006)
Abstract
We obtain common fixed point results for generalized  -nonexpansive
-nonexpansive  -subweakly commuting maps on nonstarshaped domain. As applications, we establish noncommutative versions of various best approximation results for this class of maps in certain metrizable topological vector spaces.
-subweakly commuting maps on nonstarshaped domain. As applications, we establish noncommutative versions of various best approximation results for this class of maps in certain metrizable topological vector spaces.
References
Al-Thagafi MA: Common fixed points and best approximation. Journal of Approximation Theory 1996,85(3):318–323. 10.1006/jath.1996.0045
Berinde V: A common fixed point theorem for quasi contractive type mappings. Annales Universitatis Scientiarum Budapestinensis de Rolando Eötvös Nominatae. Sectio Mathematica 2003, 46: 101–110 (2004).
Dotson WG Jr.: Fixed point theorems for non-expansive mappings on star-shaped subsets of Banach spaces. Journal of the London Mathematical Society. Second Series 1971/1972, 4: 408–410.
Guseman LF Jr., Peters BC Jr.: Nonexpansive mappings on compact subsets of metric linear spaces. Proceedings of the American Mathematical Society 1975, 47: 383–386. 10.1090/S0002-9939-1975-0353072-2
Habiniak L: Fixed point theorems and invariant approximations. Journal of Approximation Theory 1989,56(3):241–244. 10.1016/0021-9045(89)90113-5
Hussain N, Khan AR: Common fixed-point results in best approximation theory. Applied Mathematics Letters. An International Journal of Rapid Publication 2003,16(4):575–580. 10.1016/S0893-9659(03)00039-9
Hussain N, O'Regan D, Agarwal RP: Common fixed point and invariant approximation results on non-starshaped domain. Georgian Mathematical Journal 2005,12(4):559–669.
Jungck G: Common fixed points for commuting and compatible maps on compacta. Proceedings of the American Mathematical Society 1988,103(3):977–983. 10.1090/S0002-9939-1988-0947693-2
Khan LA, Khan AR: An extension of Brosowski-Meinardus theorem on invariant approximation. Approximation Theory and its Applications. New Series 1995,11(4):1–5.
Meinardus G: Invarianz bei linearen Approximationen. Archive for Rational Mechanics and Analysis 1963, 14: 301–303.
Naimpally SA, Singh KL, Whitfield JHM: Fixed points and nonexpansive retracts in locally convex spaces. Polska Akademia Nauk. Fundamenta Mathematicae 1984,120(1):63–75.
Rudin W: Functional Analysis, International Series in Pure and Applied Mathematics. 2nd edition. McGraw-Hill, New York; 1991.
Sahab SA, Khan MS, Sessa S: A result in best approximation theory. Journal of Approximation Theory 1988,55(3):349–351. 10.1016/0021-9045(88)90101-3
Shahzad N: A result on best approximation. Tamkang Journal of Mathematics 1998,29(3):223–226.
Shahzad N: Correction to: "A result on best approximation". Tamkang Journal of Mathematics 1999.,30(2): 165
Shahzad N: Noncommuting maps and best approximations. Radovi Matematički 2000/2001,10(1):77–83.
Shahzad N: Invariant approximations and
 -subweakly commuting maps. Journal of Mathematical Analysis and Applications 2001,257(1):39–45. 10.1006/jmaa.2000.7274
-subweakly commuting maps. Journal of Mathematical Analysis and Applications 2001,257(1):39–45. 10.1006/jmaa.2000.7274Shahzad N: Invariant approximations, generalized
 -contractions, and
-contractions, and  -subweakly commuting maps. Fixed Point Theory and Applications 2005,2005(1):79–86. 10.1155/FPTA.2005.79
-subweakly commuting maps. Fixed Point Theory and Applications 2005,2005(1):79–86. 10.1155/FPTA.2005.79Singh SP: An application of a fixed-point theorem to approximation theory. Journal of Approximation Theory 1979,25(1):89–90. 10.1016/0021-9045(79)90036-4
Talman LA: A fixed point criterion for compact
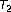 -spaces. Proceedings of the American Mathematical Society 1975, 51: 91–93.
-spaces. Proceedings of the American Mathematical Society 1975, 51: 91–93.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hussain, N., Berinde, V. Common fixed point and invariant approximation results in certain metrizable topological vector spaces. Fixed Point Theory Appl 2006, 23582 (2006). https://doi.org/10.1155/FPTA/2006/23582
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/FPTA/2006/23582
 -subweakly commuting maps. Journal of Mathematical Analysis and Applications 2001,257(1):39–45. 10.1006/jmaa.2000.7274
-subweakly commuting maps. Journal of Mathematical Analysis and Applications 2001,257(1):39–45. 10.1006/jmaa.2000.7274 -contractions, and
-contractions, and  -subweakly commuting maps. Fixed Point Theory and Applications 2005,2005(1):79–86. 10.1155/FPTA.2005.79
-subweakly commuting maps. Fixed Point Theory and Applications 2005,2005(1):79–86. 10.1155/FPTA.2005.79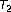 -spaces. Proceedings of the American Mathematical Society 1975, 51: 91–93.
-spaces. Proceedings of the American Mathematical Society 1975, 51: 91–93.