- Research Article
- Open access
- Published:
Hyperbolic monotonicity in the Hilbert ball
Fixed Point Theory and Applications volume 2006, Article number: 78104 (2006)
Abstract
We first characterize  -monotone mappings on the Hilbert ball by using their resolvents and then study the asymptotic behavior of compositions and convex combinations of these resolvents.
-monotone mappings on the Hilbert ball by using their resolvents and then study the asymptotic behavior of compositions and convex combinations of these resolvents.
References
Abate M: The infinitesimal generators of semigroups of holomorphic maps. Annali di Matematica Pura ed Applicata. Serie Quarta 1992,161(1):167–180. 10.1007/BF01759637
Aharonov D, Elin M, Reich S, Shoikhet D: Parametric representations of semi-complete vector fields on the unit balls in
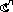 and in Hilbert space. Atti della Accademia Nazionale dei Lincei. Classe di Scienze Fisiche, Matematiche e Naturali. Rendiconti Lincei. Serie IX. Matematica e Applicazioni 1999,10(4):229–253.
and in Hilbert space. Atti della Accademia Nazionale dei Lincei. Classe di Scienze Fisiche, Matematiche e Naturali. Rendiconti Lincei. Serie IX. Matematica e Applicazioni 1999,10(4):229–253.Bauschke HH, Combettes PL, Reich S: The asymptotic behavior of the composition of two resolvents. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 2005,60(2):283–301.
Bauschke HH, Matoušková E, Reich S: Projection and proximal point methods: convergence results and counterexamples. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 2004,56(5):715–738. 10.1016/j.na.2003.10.010
Goebel K, Reich S: Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings, Monographs and Textbooks in Pure and Applied Mathematics. Volume 83. Marcel Dekker, New York; 1984:ix+170.
Halpern BR, Bergman GM: A fixed-point theorem for inward and outward maps. Transactions of the American Mathematical Society 1968, 130: 353–358. 10.1090/S0002-9947-1968-0221345-0
Kuczumow T: Nonexpansive retracts and fixed points of nonexpansive mappings in the Cartesian product of
 Hilbert balls. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 1985,9(6):601–604. 10.1016/0362-546X(85)90043-4
Hilbert balls. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 1985,9(6):601–604. 10.1016/0362-546X(85)90043-4Kuczumow T, Stachura A: Extensions of nonexpansive mappings in the Hilbert ball with the hyperbolic metric. I. Commentationes Mathematicae Universitatis Carolinae 1988,29(3):399–402.
Kuczumow T, Stachura A: Extensions of nonexpansive mappings in the Hilbert ball with the hyperbolic metric. II. Commentationes Mathematicae Universitatis Carolinae 1988,29(3):403–410.
Martin RH Jr.: A global existence theorem for autonomous differential equations in a Banach space. Proceedings of the American Mathematical Society 1970, 26: 307–314. 10.1090/S0002-9939-1970-0264195-6
Minty GJ: Monotone (nonlinear) operators in Hilbert space. Duke Mathematical Journal 1962,29(3):341–346. 10.1215/S0012-7094-62-02933-2
Reich S: Minimal displacement of points under weakly inward pseudo-Lipschitzian mappings. Atti della Accademia Nazionale dei Lincei. Rendiconti. Classe di Scienze Fisiche, Matematiche e Naturali 1975,59(1–2):40–44 (1976).
Reich S: On fixed point theorems obtained from existence theorems for differential equations. Journal of Mathematical Analysis and Applications 1976,54(1):26–36. 10.1016/0022-247X(76)90232-8
Reich S: Extension problems for accretive sets in Banach spaces. Journal of Functional Analysis 1977,26(4):378–395. 10.1016/0022-1236(77)90022-2
Reich S: Averaged mappings in the Hilbert ball. Journal of Mathematical Analysis and Applications 1985,109(1):199–206. 10.1016/0022-247X(85)90187-8
Reich S: The alternating algorithm of von Neumann in the Hilbert ball. Dynamic Systems and Applications 1993,2(1):21–25.
Reich S, Shafrir I: Nonexpansive iterations in hyperbolic spaces. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 1990,15(6):537–558. 10.1016/0362-546X(90)90058-O
Reich S, Shoikhet D: Generation theory for semigroups of holomorphic mappings in Banach spaces. Abstract and Applied Analysis 1996,1(1):1–44. 10.1155/S1085337596000012
Reich S, Shoikhet D: Semigroups and generators on convex domains with the hyperbolic metric. Atti della Accademia Nazionale dei Lincei. Classe di Scienze Fisiche, Matematiche e Naturali. Rendiconti Lincei. Serie IX. Matematica e Applicazioni 1997,8(4):231–250.
Shafrir I: Coaccretive operators and firmly nonexpansive mappings in the Hilbert ball. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 1992,18(7):637–648. 10.1016/0362-546X(92)90003-W
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kopecká, E., Reich, S. Hyperbolic monotonicity in the Hilbert ball. Fixed Point Theory Appl 2006, 78104 (2006). https://doi.org/10.1155/FPTA/2006/78104
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/FPTA/2006/78104
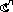 and in Hilbert space. Atti della Accademia Nazionale dei Lincei. Classe di Scienze Fisiche, Matematiche e Naturali. Rendiconti Lincei. Serie IX. Matematica e Applicazioni 1999,10(4):229–253.
and in Hilbert space. Atti della Accademia Nazionale dei Lincei. Classe di Scienze Fisiche, Matematiche e Naturali. Rendiconti Lincei. Serie IX. Matematica e Applicazioni 1999,10(4):229–253. Hilbert balls. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 1985,9(6):601–604. 10.1016/0362-546X(85)90043-4
Hilbert balls. Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods 1985,9(6):601–604. 10.1016/0362-546X(85)90043-4