- Research
- Open access
- Published:
Some extragradient methods for common solutions of generalized equilibrium problems and fixed points of nonexpansive mappings
Fixed Point Theory and Applications volume 2011, Article number: 12 (2011)
Abstract
In this article, we introduce some new iterative schemes based on the extragradient method (and the hybrid method) for finding a common element of the set of solutions of a generalized equilibrium problem, and the set of fixed points of a family of infinitely nonexpansive mappings and the set of solutions of the variational inequality for a monotone, Lipschitz-continuous mapping in Hilbert spaces. We obtain some strong convergence theorems and weak convergence theorems. The results in this article generalize, improve, and unify some well-known convergence theorems in the literature.
1. Introduction
Let H be a real Hilbert space with inner product 〈.,.〉 and induced norm ||·||. Let C be a nonempty closed convex subset of H. Let F be a bifunction from C × C to R and let B : C → H be a nonlinear mapping, where R is the set of real numbers. Moudafi [1], Moudafi and Thera [2], Peng and Yao [3, 4], Takahashi and Takahashi [5] considered the following generalized equilibrium problem:

The set of solutions of (1.1) is denoted by GEP(F, B). If B = 0, the generalized equilibrium problem (1.1) becomes the equilibrium problem for F : C × C → R, which is to find x ∈ C such that

The set of solutions of (1.2) is denoted by EP(F).
The problem (1.1) is very general in the sense that it includes, as special cases, optimization problems, variational inequalities, minimax problems, Nash equilibrium problem in noncooperative games, and others; see for instance [1–7].
Recall that a mapping S : C → C is nonexpansive if there holds that

We denote the set of fixed points of S by Fix(S).
Let the mapping A : C → H be monotone and k-Lipschitz-continuous. The variational inequality problem is to find x ∈ C such that

for all y ∈ C. The set of solutions of the variational inequality problem is denoted by V I(C, A).
Several algorithms have been proposed for finding the solution of problem (1.1). Moudafi [1] introduced an iterative scheme for finding a common element of the set of solutions of problem (1.1) and the set of fixed points of a nonexpansive mapping in a Hilbert space, and proved a weak convergence theorem. Moudafi and Thera [2] introduced an auxiliary scheme for finding a solution of problem (1.1) in a Hilbert space and obtained a weak convergence theorem. Peng and Yao [3, 4] introduced some iterative schemes for finding a common element of the set of solutions of problem (1.1), the set of fixed points of a nonexpansive mapping and the set of solutions of the variational inequality for a monotone, Lipschitz-continuous mapping and obtain both strong convergence theorems, and weak convergence theorems for the sequences generated by the corresponding processes in Hilbert spaces. Takahashi and Takahashi [5] introduced an iterative scheme for finding a common element of the set of solutions of problem (1.1) and the set of fixed points of a nonexpansive mapping in a Hilbert space, and proved a strong convergence theorem.
Some methods also have been proposed to solve the problem (1.2); see, for instance, [8–19] and the references therein. Takahashi and Takahashi [9] introduced an iterative scheme by the viscosity approximation method for finding a common element of the set of solutions of problem (1.2) and the set of fixed points of a non-expansive mapping, and proved a strong convergence theorem in a Hilbert space. Su et al. [10] introduced and researched an iterative scheme by the viscosity approximation method for finding a common element of the set of solutions of problem (1.2) and the set of fixed points of a nonexpansive mapping and the set of solutions of the variational inequality problem for an α-inverse-strongly monotone mapping in a Hilbert space. Tada and Takahashi [11] introduced two iterative schemes for finding a common element of the set of solutions of problem (1.2) and the set of fixed points of a nonexpansive mapping in a Hilbert space, and obtained both strong convergence and weak convergence theorems. Plubtieng and Punpaeng [12] introduced an iterative processes based on the extragradient method for finding the common element of the set of fixed points of a nonexpansive mapping, the set of solutions of an equilibrium problem and the set of solutions of variational inequality problem for an α-inverse-strongly monotone mapping. Chang et al. [13] introduced an iterative processes based on the extragradient method for finding the common element of the set of solutions of an equilibrium problem, the set of common fixed point for a family of infinitely nonexpansive mappings and the set of solutions of variational inequality problem for an α-inverse-strongly monotone mapping. Yao et al. [14] and Ceng and Yao [15] introduced some iterative viscosity approximation schemes for finding the common element of the set of solutions of problem (1.2) and the set of fixed points of a family of infinitely nonexpansive mappings in a Hilbert space. Colao et al. [16] introduced an iterative viscosity approximation scheme for finding a common element of the set of solutions of problem (1.2) and the set of fixed points of a family of finitely nonexpansive mappings in a Hilbert space. We observe that the algorithms in [13–16] involves the W-mapping generated by a family of infinitely (finitely) nonexpansive mappings which is an effective tool in nonlinear analysis (see [20, 21]). However, the W-mapping generated by a family of infinitely (finitely) nonexpansive mappings is too completed to use for finding the common element of the set of solutions of problem (1.2) and the set of fixed points of a family of infinitely (finitely) nonexpansive mappings. It is natural to raise and to give an answer to the following question: Can one construct algorithms for finding a common element of the set of solutions of a generalized equilibrium problem (an equilibrium problem), the common set of fixed points of a family of infinitely nonexpansive mappings and the set of solutions of a variational inequality without the W-mapping generated by a family of infinitely (finitely) nonexpansive mappings? In this article, we will give a positive answer to this question.
Recently, OHaraa et al. [22] introduced and researched an iterative approach for finding a nearest point of infinitely many nonexpansive mappings in a Hilbert spaces without using the W-mapping generated by a family of infinitely (finitely) nonexpansive mappings. Inspired by the ideas in [1–6, 8–16, 22] and the references therein, we introduce some new iterative schemes based on the extragradient method (and the hybrid method) for finding a common element of the set of solutions of a generalized equilibrium problem, the set of fixed points of a family of infinitely nonexpansive mappings, and the set of solutions of the variational inequality for a monotone, Lipschitz--continuous mapping without using the W-mapping generated by a family of infinitely (finitely) nonexpansive mappings. We obtain both strong convergence theorems and weak convergence theorems for the sequences generated by the corresponding processes. The results in this article generalize, improve, and unify some well-known convergence theorems in the literature.
2. Preliminaries
Let H be a real Hilbert space with inner product 〈·,·〉 and norm ||·||. Let C be a nonempty closed convex subset of H. Let symbols → and ⇀ denote strong and weak convergences, respectively. In a real Hilbert space H, it is well known that

for all x, y ∈ H and λ ∈ [0, 1].
For any x ∈ H, there exists the unique nearest point in C, denoted by P C (x), such that ||x - P C (x)|| ≤ ||x - y|| for all y ∈ C. The mapping P C is called the metric projection of H onto C. We know that P C is a nonexpansive mapping from H onto C. It is also known that P C x ∈ C and

for all x ∈ H and y ∈ C.
It is easy to see that (2.1) is equivalent to

for all x ∈ H and y ∈ C.
A mapping A of C into H is called monotone if

for all x, y ∈ C. A mapping A of C into H is called α-inverse-strongly monotone if there exists a positive real number α such that

for all x, y ∈ C. A mapping A : C → H is called k-Lipschitz-continuous if there exists a positive real number k such that

for all x, y ∈ C. It is easy to see that if A is α-inverse-strongly monotone, then A is monotone and Lipschitz-continuous. The converse is not true in general. The class of α-inverse-strongly monotone mappings does not contain some important classes of mappings even in a finite-dimensional case. For example, if the matrix in the corresponding linear complementarity problem is positively semidefinite, but not positively definite, then the mapping A will be monotone and Lipschitz-continuous, but not α-inverse-strongly monotone (see [23]).
Let A be a monotone mapping of C into H. In the context of the variational inequality problem, the characterization of projection (2.1) implies the following:

and

It is also known that H satisfies the Opial's condition [24], i.e., for any sequence {x n } ⊂ H with x n ⇀ x, the inequality

holds for every y ∈ H with x ≠ y.
A set-valued mapping T : H → 2 H is called monotone if for all x, y ∈ H, f ∈ Tx and g ∈ Ty imply 〈x - y, f - g〉 ≥ 0. A monotone mapping T : H → 2 H is maximal if its graph G(T) of T is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping T is maximal if and only if for (x, f) ∈ H × H, 〈x - y, f - g〉 ≥ 0 for every (y, g) ∈ G(T) implies f ∈ Tx. Let A be a monotone, k-Lipschitz-continuous mapping of C into H and N C v be normal cone to C at v ∈ C, i.e., N C v = {w ∈ H : 〈v - u, w〉 ≥ 0, ∀u ∈ C}. Define

Then, T is maximal monotone and 0 ∈ Tv if and only if v ∈ V I(C, A) (see [25]).
For solving the equilibrium problem, let us assume that the bifunction F satisfies the following condition:
(A1) F(x, x) = 0 for all x ∈ C;
(A2) F is monotone, i.e., F(x, y) + F(y, x) ≤ 0 for any x, y ∈ C;
(A3) for each x, y, z ∈ C,

(A4) for each x ∈ C, y ↦ F(x, y) is convex and lower semicontinuous.
We recall some lemmas which will be needed in the rest of this article.
Lemma 2.1.[7] Let C be a nonempty closed convex subset of H, let F be a bifunction from C × C to R satisfying (A1)-(A4). Let r > 0 and x ∈ H. Then, there exists z ∈ C such that

Lemma 2.2.[8] Let C be a nonempty closed convex subset of H, let F be a bi-function from C × C to R satisfying (A1)-(A4). For r > 0 and x ∈ H, define a mapping Tr : H → C as follows:

for all x ∈ H. Then, the following statements hold:
-
(1)
T r is single-valued;
-
(2)
T r is firmly nonexpansive, i.e., for any x, y ∈ H,
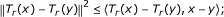
-
(3)
F(T r ) = EP (F);
-
(4)
EP(F) is closed and convex.
3. The main results
We first show a strong convergence of an iterative algorithm based on extragradient and hybrid methods which solves the problem of finding a common element of the set of solutions of a generalized equilibrium problem, the set of fixed points of a family of infinitely nonexpansive mappings, and the set of solutions of the variational inequality for a monotone, Lipschitz-continuous mapping in a Hilbert space.
Theorem 3.1. Let C be a nonempty closed convex subset of a real Hilbert space H. Let F be a bifunction from C × C to R satisfying (A1)-(A4). Let A be a monotone and k-Lipschitz-continuous mapping of C into H and B be an α-inverse-strongly monotone mapping of C into H. Let S1, S2,... be a family of infinitely nonexpansive mappings of C into itself such that  . Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds
. Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds

Let {x n }, {u n }, {y n } and {z n } be sequences generated by

for every n = 1, 2,... where {λ
n
} ⊂ [a, b] for some  , {r
n
} ⊂ [d, e] for some d, e ∈ (0, 2α), and {α
n
}, {β
n
}, {γ
n
} are three sequences in [0, 1] satisfying the conditions:
, {r
n
} ⊂ [d, e] for some d, e ∈ (0, 2α), and {α
n
}, {β
n
}, {γ
n
} are three sequences in [0, 1] satisfying the conditions:
-
(i)
α n + β n ≤ 1 for all n ∈ N;
-
(ii)
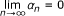 ;
; -
(iii)
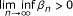 ;
; -
(iv)
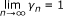 and
and 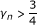 for all n ∈ N;
for all n ∈ N;
Then, {x n }, {u n }, {y n } and {z n } converge strongly to w = PΩ(x).
Proof. It is obvious that C n is closed, and Q n is closed and convex for every n = 1, 2,.... Since

we also have that C
n
is convex for every n = 1, 2,.... It is easy to see that 〈x
n
- z, x - x
n
〉 ≥ 0 for all z ∈ Q
n
and by (2.1),  . Let t
n
= P
C
(u
n
- λ
n
Ay
n
) for every n = 1, 2,.... Let u ∈ Ω and let
. Let t
n
= P
C
(u
n
- λ
n
Ay
n
) for every n = 1, 2,.... Let u ∈ Ω and let  >be a sequence of mappings defined as in Lemma 2.2. Then
>be a sequence of mappings defined as in Lemma 2.2. Then  . From
. From  and the α-inverse strongly monotonicity of B, we have
and the α-inverse strongly monotonicity of B, we have

From (2.2), the monotonicity of A, and u ∈ V I(C, A), we have

Further, Since y n = (1 - γ n )u n + γ n P C (u n - λ n Au n ) and A is k-Lipschitz-continuous, we have

In addition, from the definition of P C , we have

It follows from  ,
, 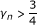 and (3.2) that
and (3.2) that

In addition, from u ∈ V I(C, A) and (3.2), we have

Therefore, from (3.2) to (3.4) and z n = (1 - α n - β n )x n + α n y n + β n S n t n and u = S n u, we have

for every n = 1, 2,... and hence u ∈ C
n
. So, Ω ⊂ C
n
for every n = 1, 2,.... Next, let us show by mathematical induction that x
n
is well defined and Ω ⊂ C
n
∩ Q
n
for every n = 1, 2,.... For n = 1 we have x1 = x ∈ C and Q1 = C. Hence, we obtain Ω ⊂C1 ∩ Q1. Suppose that x
k
is given and Ω ⊂ C
k
∩ Q
k
for some k ∈ N. Since Ω is nonempty, C
k
∩ Q
k
is a nonempty closed convex subset of H. Hence, there exists a unique element xk+1∈ C
k
∩ Q
k
such that  . It is also obvious that there holds 〈xk+1- z, x - xk+1〉 ≥ 0 for every z ∈ C
k
∩ Q
k
. Since Ω ⊂ C
k
∩ Q
k
, we have 〈xk+1- z, x - xk+1〉 ≥ 0 for every z ∈ Ω and hence Ω ⊂ Qk+1. Therefore, we obtain Ω ⊂ Ck+1∩ Qk+1.
. It is also obvious that there holds 〈xk+1- z, x - xk+1〉 ≥ 0 for every z ∈ C
k
∩ Q
k
. Since Ω ⊂ C
k
∩ Q
k
, we have 〈xk+1- z, x - xk+1〉 ≥ 0 for every z ∈ Ω and hence Ω ⊂ Qk+1. Therefore, we obtain Ω ⊂ Ck+1∩ Qk+1.
Let l0 = PΩx. From  and l0 v Ω ⊂ C
n
∩ Q
n
, we have
and l0 v Ω ⊂ C
n
∩ Q
n
, we have

for every n = 1, 2,.... Therefore, {x
n
} is bounded. From (3.2) to (3.5) and the lipschitz continuity of A, we also obtain that {u
n
}, {y
n
}, {Au
n
}, {t
n
} and {z
n
} are bounded. Since xn+1∈ C
n
∩ Q
n
⊂ C
n
and  , we have
, we have

for every n = 1, 2,.... It follows from (3.6) that limn→∞||x n - x|| exists.
Since  and xn+1∈ Q
n
, using (2.2), we have
and xn+1∈ Q
n
, using (2.2), we have

for every n = 1, 2,.... This implies that

Since xn+1∈ C n , we have ||z n - xn+1||2 ≤ ||x n - xn+1||2 + (3 - 3γ n + α n )b2||Au n ||2 and hence it follows from limn→∞γ n = 1 and limn→∞α n = 0 that limn→∞||z n - xn+1|| = 0. Since

for every n = 1, 2,..., we have ||x n - z n || → 0.
For u ∈ Ω, from (3.5), we obtain

Since limn→∞γ n = 1 and limn→∞α n = 0, {x n }, {y n }, {Au n }, and {z n } are bounded, we have

By lim infn→∞β n > 0, we get

From (3.3) and u = S n u, we have

Thus, limn→∞||t n - u||2- ||x n - u||2 = 0.
From (3.3) and (3.2), we have

It follows that

The assumptions on γ
n
and λ
n
imply that  and
and  . Consequently, limn→∞||u
n
- y
n
|| = limn→∞||t
n
- y
n
|| = 0. Since A is Lipschitz-continuous, we have limn→∞||At
n
- Ay
n
|| = 0. It follows from ||u
n
- t
n
|| ≤ ||u
n
- y
n
|| + ||t
n
- y
n
|| that limn→∞||u
n
- t
n
|| = 0.
. Consequently, limn→∞||u
n
- y
n
|| = limn→∞||t
n
- y
n
|| = 0. Since A is Lipschitz-continuous, we have limn→∞||At
n
- Ay
n
|| = 0. It follows from ||u
n
- t
n
|| ≤ ||u
n
- y
n
|| + ||t
n
- y
n
|| that limn→∞||u
n
- t
n
|| = 0.
We rewrite the definition of z n as

From limn→∞||z n - x n || = 0, limn→∞α n = 0, the boundedness of {x n }, {y n } and lim infn→∞β n > 0 we infer that limn→∞||S n t n - x n || = 0.
By (3.2)-(3.5), we have

Hence, we have

Since limn→∞α n = 1, lim infn→∞β n > 0, limn→∞γ n = 1, ||x n - z n || → 0 and the sequences {x n } and {z n } are bounded, we obtain ||Bx n - B u || → 0.
For u ∈ Ω, we have, from Lemma 2.2,

Hence,

Then, by (3.5), we have

Hence,

Since limn→∞α n = 0, lim infn→∞β n > 0, limn→∞γ n = 1, ||x n - z n || → 0, ||Bx n - Bu|| → 0 and the sequences {x n }, {u n } and {z n } are bounded, we obtain ||x n - u n || → 0. From ||z n - t n || ≤ ||z n - x n ||+||x n - u n ||+||u n - t n ||, we have ||z n - t n || → 0.
From ||t n - x n || ≤ ||t n - u n || + ||x n - u n ||, we also have ||t n - x n || → 0.
Since z n = (1 - α n - β n )x n + α n y n + β n S n t n , we have β n (S n t n - t n ) = (1 - α n - β n )(t n - x n ) + α n (t n - y n ) + (z n - t n ). Then

and hence ||S n t n - t n || → 0. At the same time, observe that for all i ∈ {1, 2,...},

It follows from (3.8) and the condition (*) that for all i ∈ {1, 2,...},

As {x
n
} is bounded, there exists a subsequence  of {x
n
} such that x
ni
⇀ w. From ||x
n
- u
n
|| → 0, we obtain that u
ni
⇀ w. From ||u
n
- t
n
|| → 0, we also obtain that t
ni
⇀ w. Since {u
ni
} ⊂ C and C is closed and convex, we obtain w ∈ C.
of {x
n
} such that x
ni
⇀ w. From ||x
n
- u
n
|| → 0, we obtain that u
ni
⇀ w. From ||u
n
- t
n
|| → 0, we also obtain that t
ni
⇀ w. Since {u
ni
} ⊂ C and C is closed and convex, we obtain w ∈ C.
First, we show w ∈ GEP(F, B). By  , we know that
, we know that

It follows from (A2) that

Hence,

For t with 0 < t ≤ 1 and y ∈ C, let y t = t y + (1 - t)w. Since y ∈ C and w ∈ C, we obtain y t ∈ C. So, from (3.10) we have

Since  , we have
, we have  . Further, from the inverse-strongly monotonicity of B, we have
. Further, from the inverse-strongly monotonicity of B, we have  . Hence, from (A4),
. Hence, from (A4),  and
and  , we have
, we have

as i → ∞. From (A1), (A4) and (3.11), we also have

and hence

Letting t → 0, we have, for each y ∈ C,

This implies that w ∈ GEP(F, B).
We next show that  . Assume
. Assume  . Since
. Since  and
and  for some i0 ∈ {1, 2,...} from the Opial condition, we have
for some i0 ∈ {1, 2,...} from the Opial condition, we have

This is a contradiction. Hence, we get  .
.
Finally we show w ∈ V I(C, A). Let

where N C v is the normal cone to C at v ∈ C. We have already mentioned that in this case the mapping T is maximal monotone, and 0 ∈ Tv if and only if v ∈ V I(C, A). Let (v, g) ∈ G(T). Then Tv = Av + N C v and hence g - Av ∈ N C v.
Hence, we have 〈v - t, g - Av〉 ≥ 0 for all t ∈ C. On the other hand, from t n = P C (u n - λ n Ay n ) and v ∈ C, we have

and hence

Therefore, we have

Hence, we obtain 〈v - w, g〉 ≥ 0 as i → ∞. Since T is maximal monotone, we have w ∈ T-10 and hence w ∈ V I(C, A). This implies that w ∈ Ω.
From l0 = PΩx, w ∈ Ω and (3.6), we have

Hence, we obtain

From  , we have
, we have  , and hence
, and hence  . Since
. Since  and l0 ∈ Ω ⊂ C
n
∩ Q
n
⊂ Q
n
, we have
and l0 ∈ Ω ⊂ C
n
∩ Q
n
⊂ Q
n
, we have

As i → ∞, we obtain - ||l0- w||2 ≥ 〈l0- w, x - l0〉 ≥ 0 by l0 = PΩx and w ∈ Ω. Hence, we have w = l0. This implies that x n → l0. It is easy to see u n → l0, y n → l0 and z n → l0. The proof is now complete.
By combining the arguments in the proof of Theorem 3.1 and those in the proof of Theorem 3.1 in [3], we can easily obtain the following weak convergence theorem for an iterative algorithm based on the extragradient method which solves the problem of finding a common element of the set of solutions of a generalized equilibrium problem, the set of fixed points of a family of infinitely nonexpansive mappings and the set of solutions of the variational inequality for a monotone, Lipschitz-continuous mapping in a Hilbert space.
Theorem 3.2. Let C be a nonempty closed convex subset of a real Hilbert space H. Let F be a bifunction from C × C to R satisfying (A1)-(A4). Let A be a monotone, and k-Lipschitz-continuous mapping of C into H and B be an α-inverse-strongly monotone mapping of C into H. Let S1, S2,... be a family of infinitely nonexpansive mappings of C into itself such that  . Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds
. Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds

Let {x n }, {u n } and {y n } be the sequences generated by

for every n = 1, 2,.... If {λ
n
} ⊂ [a, b] for some  , {β
n
} ⊂ [δ, ε] for some δ, ε ∈ (0, 1) and {r
n
} ⊂ [d, e] for some d, e ∈ (0, 2α). Then, {x
n
}, {u
n
} and {y
n
} converge weakly to w ∈ Ω, where w = limn→∞PΩx
n
.
, {β
n
} ⊂ [δ, ε] for some δ, ε ∈ (0, 1) and {r
n
} ⊂ [d, e] for some d, e ∈ (0, 2α). Then, {x
n
}, {u
n
} and {y
n
} converge weakly to w ∈ Ω, where w = limn→∞PΩx
n
.
4. Applications
By Theorems 3.1 and 3.2, we can obtain many new and interesting convergence theorems in a real Hilbert space. We give some examples as follows:
Let A = 0, by Theorems 3.1 and 3.2, respectively, we obtain the following results.
Theorem 4.1. Let C be a nonempty closed convex subset of a real Hilbert space H. Let F be a bifunction from C×C to R satisfying (A1)-(A4). Let B be an α-inverse-strongly monotone mapping of C into H. Let S1, S2,... be a family of infinitely nonexpansive mappings of C into itself such that  . Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds
. Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds

Let {x n }, {u n } {y n }, and {z n } be the sequences generated by

for every n = 1, 2,.... where {r n } ⊂ [d, e] for some d, e ∈ (0, 2α), and {α n }, {β n } are sequences in [0, 1] satisfying the conditions:
-
(i)
α n + β n ≤ 1 for all n ∈ N;
-
(ii)
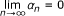 ;
; -
(iii)
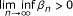 for all n ∈ N;
for all n ∈ N;
Then, {x n }, {u n }, and {z n } converge strongly to w = P∑(x).
Theorem 4.2. Let C be a nonempty closed convex subset of a real Hilbert space H. Let F be a bifunction from C×C to R satisfying (A1)-(A4). Let B be an α-inverse-strongly monotone mapping of C into H. Let S1, S2,... be a family of infinitely nonexpansive mappings of C into itself such that  . Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds
. Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds

Let {x n } and {u n } be sequences generated by

for every n = 1, 2,.... If {β n } ⊂ [δ, ε] for some δ, ε ∈ (0, 1) and {r n } ⊂ [d, e] for some d, e ∈ (0, 2α). Then, {x n } and {u n } converge weakly to w ∈ ∑, where w = limn→∞P∑x n .
Theorem 4.3. Let C be a nonempty closed convex subset of a real Hilbert space H. Let F be a bifunction from C×C to R satisfying (A1)-(A4). Let A be a monotone and k-Lipschitz-continuous mapping of C into H and B be an α-inverse-strongly monotone mapping of C into H. Let S1, S2,... be a family of infinitely nonexpansive mappings of C into itself such that  . Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds
. Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds

Let {x n }, {u n }, {y n }, and {z n } be sequences generated by

for every n = 1, 2,... where {λ
n
} ⊂ [a, b] for some  , {r
n
} ⊂ [d, e] for some d, e ∈ (0, 2α), and {β
n
} is a sequence in [0, 1] satisfying
, {r
n
} ⊂ [d, e] for some d, e ∈ (0, 2α), and {β
n
} is a sequence in [0, 1] satisfying 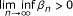 . Then, {x
n
}, {u
n
}, {y
n
}, and {z
n
} converge strongly to w = PΩ(x).
. Then, {x
n
}, {u
n
}, {y
n
}, and {z
n
} converge strongly to w = PΩ(x).
Proof. Putting γ n = 1 and α n = 0, by Theorem 3.1, we obtain the desired result.
Let B = 0, by Theorems 3.1, 3.2, and 4.3, we obtain the following results.
Theorem 4.4. Let C be a nonempty closed convex subset of a real Hilbert space H. Let F be a bifunction from C×C to R satisfying (A1)-(A4). Let A be a monotone and k-Lipschitz-continuous mapping of C into H. Let S1, S2,... be a family of infinitely nonexpansive mappings of C into itself such that  . Assume that for all i ∈ {1, 2,...}, and for any bounded subset K of C, there holds
. Assume that for all i ∈ {1, 2,...}, and for any bounded subset K of C, there holds

Let {x n }, {u n }, {y n }, and {z n } be the sequences generated by

for every n = 1, 2,.... where {λ
n
} ⊂ [a, b] for some  , {r
n
} ⊂ [d, +∞) for some d > 0, and {α
n
}, {β
n
}, {γ
n
} are three sequences in [0, 1] satisfying the following conditions:
, {r
n
} ⊂ [d, +∞) for some d > 0, and {α
n
}, {β
n
}, {γ
n
} are three sequences in [0, 1] satisfying the following conditions:
-
(i)
α n + β n ≤ 1 for all n ∈ N;
-
(ii)
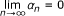 ;
; -
(iii)
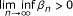 ;
; -
(iv)
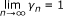 and
and 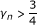 for all n ∈ N;
for all n ∈ N;
Then, {x n }, {u n }, {y n } and {z n } converge strongly to w = PΛ(x).
Theorem 4.5. Let C be a nonempty closed convex subset of a real Hilbert space H. Let F be a bifunction from C×C to R satisfying (A1)-(A4). Let A be a monotone and k-Lipschitz-continuous mapping of C into H. Let S1, S2,... be a family of infinitely nonexpansive mappings of C into itself such that  . Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds
. Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds

Let {x n }, {u n }, and {y n } be the sequences generated by

for every n = 1, 2,.... If {λ
n
} ⊂ [a, b] for some  ,{β
n
} ⊂ [δ, ε], for some δ, ε ∈ (0, 1) and {r
n
} ⊂ [d, +∞] for some d > 0, then {x
n
}, {u
n
} and {y
n
} converge weakly to w ∈ Λ, where w = limn→∞PΛx
n
.
,{β
n
} ⊂ [δ, ε], for some δ, ε ∈ (0, 1) and {r
n
} ⊂ [d, +∞] for some d > 0, then {x
n
}, {u
n
} and {y
n
} converge weakly to w ∈ Λ, where w = limn→∞PΛx
n
.
Theorem 4.6. Let C be a nonempty closed convex subset of a real Hilbert space H. Let F be a bifunction from C × C to R satisfying (A1)-(A4). Let A be a monotone and k-Lipschitz-continuous mapping of C into H. Let S1, S2,... be a family of infinitely nonexpansive mappings of C into itself such that  . Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds
. Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds

Let {x n }, {u n } {y n }, and {z n } be the sequences generated by

for every n = 1, 2,.... where {λ
n
} ⊂ [a, b] for some  , {r
n
} ⊂ [d, +∞) and for some d > 0, and {β
n
} is a sequence in [0, 1] satisfying
, {r
n
} ⊂ [d, +∞) and for some d > 0, and {β
n
} is a sequence in [0, 1] satisfying 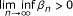 . Then, {x
n
}, {u
n
}, {y
n
}, and {z
n
} converge strongly to w = PΛ(x).
. Then, {x
n
}, {u
n
}, {y
n
}, and {z
n
} converge strongly to w = PΛ(x).
Let B = 0 and F(x, y) = 0 for x, y ∈ C, by Theorems 3.1 and 4.3, we obtain the following results.
Theorem 4.7. Let C be a nonempty closed convex subset of a real Hilbert space H. Let A be a monotone and k-Lipschitz-continuous mapping of C into H. Let S1, S2,... be a family of infinitely nonexpansive mappings of C into itself such that  . Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds
. Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds

Let {x n }, {y n }, and {z n } be the sequences generated by

for every n = 1, 2,.... where {λ
n
} ⊂ [a, b] for some  , and {α
n
}, {β
n
}, {γ
n
}are three sequences in [0, 1] satisfying the following conditions:
, and {α
n
}, {β
n
}, {γ
n
}are three sequences in [0, 1] satisfying the following conditions:
-
(i)
α n + β n ≤ 1 for all n ∈ N;
-
(ii)
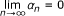 ;
; -
(iii)
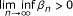 ;
; -
(iv)
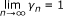 and
and 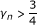 for all n ∈ N;
for all n ∈ N;
Then, {x n }, {y n }, and {z n } converge strongly to w = PΓ(x).
Theorem 4.8. Let C be a nonempty closed convex subset of a real Hilbert space H. Let A be a monotone and k-Lipschitz-continuous mapping of C into H. Let S1, S2,... be a family of infinitely nonexpansive mappings of C into itself such that  . Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds
. Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds

Let {x n }, {y n }, and {z n } be the sequences generated by

for every n = 1, 2,.... where {λ
n
} ⊂ [a, b] for some  , and {β
n
} is a sequence in [0, 1] satisfying
, and {β
n
} is a sequence in [0, 1] satisfying 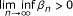 . Then, {x
n
}, {y
n
}, and {z
n
} converge strongly to w = PΓ(x).
. Then, {x
n
}, {y
n
}, and {z
n
} converge strongly to w = PΓ(x).
Let F(x, y) = 0 for x, y ∈ C, then by Theorem 3.2 and the proof of Theorem 4.7 in [3], we obtain the following result.
Theorem 4.9. Let C be a nonempty closed convex subset of a real Hilbert space H. Let A be a monotone and k-Lipschitz-continuous mapping of C into H and B be an α-inverse-strongly monotone mapping of C into H. Let S1, S2,... be a family of infinitely nonexpansive mappings of C into itself such that  . Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds
. Assume that for all i ∈ {1, 2,...} and for any bounded subset K of C, thenthere holds

Let {x n }, {u n }, and {y n } be the sequences generated by

for every n = 1, 2,.... if {λ
n
} ⊂ [a, b] for some  , {β
n
} ⊂ [δ, ε] for some δ, ε ∈ (0, 1) and {r
n
} ⊂ [d, e] for some d, e ∈ (0, 2α). Then, {x
n
} and {u
n
} converge weakly to w ∈ Ξ, where w = limn→∞PΞx
n
.
, {β
n
} ⊂ [δ, ε] for some δ, ε ∈ (0, 1) and {r
n
} ⊂ [d, e] for some d, e ∈ (0, 2α). Then, {x
n
} and {u
n
} converge weakly to w ∈ Ξ, where w = limn→∞PΞx
n
.
Remark 4.1.
-
(i)
For all n ≥ 1, let S n = S be a nonexpansive mapping, by Theorems 3.2, 4.2, 4.7, 4.8, and 4.9 we recover Theorem 3.1 in [5], Theorem 3.1 in [1], Theorem 5 in [26], Theorem 3.1 in [23], and Theorem 4.7 in [3]. In addition, let A = 0, by Theorems 4.6 and 4.5, respectively, we recover Theorems 3.1 and 4.1 in [11].
-
(ii)
For all n ≥ 1, let S n = S be a nonexpansive mapping, by Theorems 3.1, 4.3, and 4.4, respectively, we recover Theorems 4.3, 4.4, and 4.7 in [4] with some modified conditions on F.
-
(iii)
Theorems 3.1, 3.2, 4.3-4.7 also improve the main results in [10, 12, 13] because the inverse strongly monotonicity of A has been replaced by the monotonicity and Lipschitz continuity of A.
The following result illustrates that there are the nonexpansive mappings S1, S2 ,... satisfying the condition (*).
Lemma 4.1. Let C be a nonempty closed convex subset of a real Hilbert space H. Let T be a nonexpansive mapping of C into itself such that Fix(T) ≠ ∅. If we define  for n ∈ {1, 2,...}, and x ∈ C, then the following results hold:
for n ∈ {1, 2,...}, and x ∈ C, then the following results hold:
-
(a)
For any bounded subset K of C, there holds
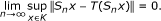
-
(b)
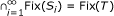 .
. -
(c)
for all i ∈ {1, 2,...} and for any bounded subset K of C, there holds
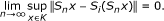
Proof.
-
(a)
It is due to Bruck [27, 28] (please also see Lemma 3.1 in [22]).
-
(b)
It follows from (a) that
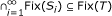 .
.Moreover, it is obvious that
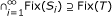 . Hence,
. Hence, 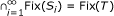 .
. -
(c)
It can be proved by mathematical induction. In fact, it is clear that this conclusion holds for i = 1. Assume that the conclusion holds for i = m, that is, for any bounded subset K of C, there holds
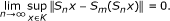 (4.1)
(4.1)
We now prove that the conclusion also holds for i = m + 1. In fact, we observe that

It is easy to verify that S1, S2,... are nonexpansive mappings. It follows from (4.1) and (4.2) that for any bounded subset K of C, there holds

From Lemma 4.1, we know that by Theorems 3.1 and 3.2, respectively, we can obtain the following results.
Theorem 4.10. Let C be a nonempty closed convex subset of a real Hilbert space H. Let F be a bifunction from C × C to R satisfying (A1)-(A4). Let A be a monotone and k-Lipschitz-continuous mapping of C into H and B be an α-inverse-strongly monotone mapping of C into H. Let T be a nonexpansive mapping of C into itself such that Θ = Fix(T)∩VI(C, A)∩GEP(F, B) ≠ ∅. Let {λ
n
} ⊂ [a, b] for some  , {r
n
} ⊂ [d, e] and for some d, e ∈ (0, 2α), and {α
n
}, {β
n
}, and {γ
n
} be three sequences in [0, 1] satisfying the following conditions:
, {r
n
} ⊂ [d, e] and for some d, e ∈ (0, 2α), and {α
n
}, {β
n
}, and {γ
n
} be three sequences in [0, 1] satisfying the following conditions:
-
(i)
α n + β n ≤ 1 for all n ∈ N;
-
(ii)
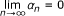 ;
; -
(iii)
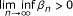 ;
; -
(iv)
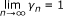 and
and 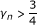 for all n ∈ N; If we define
for all n ∈ N; If we define  for n ∈ {1, 2,...}, and x ∈ C, then the sequences {x
n
}, {u
n
}, {y
n
}, and {z
n
} generated by algorithm (3.1) converge strongly to w = P Θ(x).
for n ∈ {1, 2,...}, and x ∈ C, then the sequences {x
n
}, {u
n
}, {y
n
}, and {z
n
} generated by algorithm (3.1) converge strongly to w = P Θ(x).
Theorem 4.11. Let C be a nonempty closed convex subset of a real Hilbert space H. Let F be a bifunction from C × C to R satisfying (A1)-(A4). Let A be a monotone and k-Lipschitz-continuous mapping of C into H and B be an α-inverse-strongly monotone mapping of C into H, and T be a nonexpansive mapping of C into itself such that Θ = Fix(T)∩VI(C, A)∩GEP(F, B) ≠ ∅. Assume that {λ
n
} ⊂ [a, b] for some  {β
n
} ⊂ [δ, ε] for some δ, ε ∈ (0, 1), and {r
n
} ⊂ [d, e] some d, e ∈ (0, 2α). If we define
{β
n
} ⊂ [δ, ε] for some δ, ε ∈ (0, 1), and {r
n
} ⊂ [d, e] some d, e ∈ (0, 2α). If we define  for n ∈ {1, 2,...} and x ∈ C, then the sequences {x
n
}, {u
n
}, and {y
n
} generated by algorithm (3.12) converge weakly to w ∈ Θ, where w = limn→∞PΘx
n
.
for n ∈ {1, 2,...} and x ∈ C, then the sequences {x
n
}, {u
n
}, and {y
n
} generated by algorithm (3.12) converge weakly to w ∈ Θ, where w = limn→∞PΘx
n
.
References
Moudafi A: Weak convergence theorems for nonexpansive mappings and equilibrium Problems. J Nonlinear Convex Anal 2008, 9: 37–43.
Moudafi A, Thera M: Proximal and dynamical approaches to equilibrium problems. Lecture Notes in Econom and Math System, Springer-Verlag, Berlin 1999, 477: 187–201.
Peng JW, Yao JC: Weak convergence of an iterative scheme for generalized equilibrium problems. Bull Aust Math Soc 2009, 79: 437–453. 10.1017/S0004972708001378
Peng JW, Yao JC: A new hybrid-extragradient method for generalized mixed equilibrium problems and fixed point problems and variational inequality problems. Taiwan J Math 2008,12(6):1401–1432.
Takahashi S, Takahashi W: Strong convergence theorem for a generalized equilibrium problem and a nonexpansive mapping in a Hilbert space. Nonlinear Anal 2008, 69: 1025–1033. 10.1016/j.na.2008.02.042
Flam SD, Antipin AS: Equilibrium programming using proximal-like algorithms. Math Program 1997, 78: 29–41.
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. Math Stud 1994, 63: 123–145.
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. J Nonlinear Convex Anal 2005, 6: 117–136.
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. J Math Anal Appl 2006, 331: 506–515.
Su Y, Shang M, Qin X: An iterative method of solutions for equilibrium and optimization problems. Nonlinear Anal 2008, 69: 2709–2719. 10.1016/j.na.2007.08.045
Tada A, Takahashi W: Weak and strong convergence theorems for a nonexpansive mapping and an equilibrium problem. J Optim Theory Appl 2007, 133: 359–370. 10.1007/s10957-007-9187-z
Plubtieng S, Punpaeng R: A new iterative method for equilibrium problems and fixed point problems of nonexpansive mappings and monotone mappings. Appl Math Comput 2008, 197: 548–558. 10.1016/j.amc.2007.07.075
Chang SS, Joseph Lee HW, Chan CK: A new method for solving equilibrium problem, fixed point problem and variational inequality problem with application to optimization. Nonlinear Anal 2009, 70: 3307–3319. 10.1016/j.na.2008.04.035
Yao YH, Liou YC, Yao JC: Convergence theorem for equilibrium problems and fixed point problems of infinite family of nonexpansive mappings. Fixed Point Theory Appl 2007, 12. Article ID 64363
Ceng LC, Yao JC: Hybrid viscosity approximation schemes for equilibrium problems and fixed point problems of infinitely many nonexpansive mappings. Appl Math Comput 2007, 198: 729–741.
Colao V, Marino G, Xu H-K: An iterative method for finding common solutions of equilibrium and fixed point problems. J Math Anal Appl 2008, 344: 340–352. 10.1016/j.jmaa.2008.02.041
Iusem AN, Sosa W: Iterative algorithms for equilibrium problems. Optimization 2003, 52: 301–316. 10.1080/0233193031000120039
Nguyen TTV, Strodiot JJ, Nguyen VH: A bundle method for solving equilibrium problems. Math Program Ser B 2009, 116: 529–552. 10.1007/s10107-007-0112-x
Ceng LC, AI-Homidan S, Ansari QH, Yao JC: An iterative scheme for equilibrium problems and fixed point problems of strict pseudo-contraction mappings. J Comput Appl Math 2008, 223: 967–974.
Takahashi W, Shimoji K: Convergence theorems for nonexpansive mappings and feasibility problems. Math Comput Model 2000, 32: 1463–1471. 10.1016/S0895-7177(00)00218-1
Shimoji K, Takahashi W: Strong convergence to common fixed points of infinite nonexpansive mappings and applications. Taiwanese J Math 2001,5(2):387–404.
OHaraa JG, Pillay P, Xu HK: Iterative approaches to finding nearest common fixed points of nonexpansive mappings in Hilbert spaces. Nonlinear Anal 2003, 54: 1417–1426. 10.1016/S0362-546X(03)00193-7
Nadezhkina N, Takahashi W: Strong convergence theorem by a hybrid method for non-expansive mappings and Lipschitz-continuous monotone mappings. SIAM J Optim 2006,16(4):1230–1241. 10.1137/050624315
Opial Z: Weak convergence of the sequence of successive approximation for nonexpansive mappings. Bull Am Math Soc 1967, 73: 561–597.
Rockafellar RT: On the maximality of sums of nonlinear monotone operators. Trans Am Math Soc 1970, 149: 75–88. 10.1090/S0002-9947-1970-0282272-5
Ceng LC, Hadjisavvas N, Wong NC: Strong convergence theorem by a hybrid extragradient-like approximation method for variational inequalities and fixed point problems. J Global Optim 2010, 46: 635–646 (2010). 10.1007/s10898-009-9454-7
Bruck RE: A simple proof of the mean ergodic theorem for nonlinear contractions in Banach spaces. Israel J Math 1979, 32: 107–116. 10.1007/BF02764907
Bruck RE: On the convex approximation property and the asymptotic behavior of nonlinear contractions in Banach spaces. Israel J Math 1981, 38: 304–314. 10.1007/BF02762776
Acknowledgements
This research was supported by the National Natural Science Foundation of China, the Natural Science Foundation of Chongqing (Grant No. CSTC, 2009BB8240), and the Special Fund of Chongqing Key Laboratory (CSTC). The author is grateful to the referees for their detailed comments and helpful suggestions, which have improved the presentation of this article.
Author information
Authors and Affiliations
Corresponding author
Additional information
5. Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Peng, JW. Some extragradient methods for common solutions of generalized equilibrium problems and fixed points of nonexpansive mappings. Fixed Point Theory Appl 2011, 12 (2011). https://doi.org/10.1186/1687-1812-2011-12
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-12
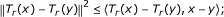
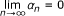 ;
;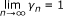 and
and 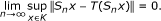
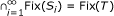 .
.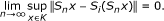
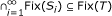 .
.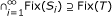 . Hence,
. Hence,