- Research
- Open access
- Published:
Coupled fixed point results in cone metric spaces for  -compatible mappings
-compatible mappings
Fixed Point Theory and Applications volume 2011, Article number: 27 (2011)
Abstract
In this paper, we introduce the concepts of  -compatible mappings, b-coupled coincidence point and b-common coupled fixed point for mappings F, G : X × X → X, where (X, d) is a cone metric space. We establish b-coupled coincidence and b-common coupled fixed point theorems in such spaces. The presented theorems generalize and extend several well-known comparable results in the literature, in particular the recent results of Abbas et al. [Appl. Math. Comput. 217, 195-202 (2010)]. Some examples are given to illustrate our obtained results. An application to the study of existence of solutions for a system of non-linear integral equations is also considered.
-compatible mappings, b-coupled coincidence point and b-common coupled fixed point for mappings F, G : X × X → X, where (X, d) is a cone metric space. We establish b-coupled coincidence and b-common coupled fixed point theorems in such spaces. The presented theorems generalize and extend several well-known comparable results in the literature, in particular the recent results of Abbas et al. [Appl. Math. Comput. 217, 195-202 (2010)]. Some examples are given to illustrate our obtained results. An application to the study of existence of solutions for a system of non-linear integral equations is also considered.
2010 Mathematics Subject Classifications: 54H25; 47H10.
1 Introduction
Ordered normed spaces and cones have applications in applied mathematics, for instance, in using Newton's approximation method [1–4] and in optimization theory [5]. K-metric and K-normed spaces were introduced in the mid-20th century ([2]; see also [3, 4, 6]) by using an ordered Banach space instead of the set of real numbers, as the codomain for a metric. Huang and Zhang [7] re-introduced such spaces under the name of cone metric spaces, and went further, defining convergent and Cauchy sequences in the terms of interior points of the underlying cone. Afterwards, many papers about fixed point theory in cone metric spaces were appeared (see, for example, [8–15]).
The following definitions and results will be needed in the sequel.
Definition 1. [4, 7]. Let E be a real Banach space. A subset P of E is called a cone if and only if:
-
(a)
P is closed, non-empty and P ≠ {0 E },
-
(b)
a, b ∈ ℝ, a, b ≥ 0, x, y ∈ P imply that ax + by ∈ P,
-
(c)
P ∩ (-P) = {0 E },
where 0 E is the zero vector of E.
Given a cone define a partial ordering ≼ with respect to P by x ≼ y if and only if y - x ∈ P. We shall write x ≪ y for y - x ∈ IntP, where IntP stands for interior of P. Also, we will use x ≺ y to indicate that x ≼ y and x ≠ y. The cone P in a normed space (E, ||·||) is called normal whenever there is a number k ≥ 1 such that for all x, y ∈ E, 0 E ≼ x ≼ y implies ||x|| ≤ k||y||. The least positive number satisfying this norm inequality is called the normal constant of P.
Definition 2. [7]. Let X be a non-empty set. Suppose that d : X × X → E satisfies:
(d1) 0 E ≼ d(x, y) for all x, y ∈ X and d(x, y) = 0 E if and only if x = y,
(d2) d(x, y) = d(y, x) for all x, y ∈ X,
(d3) d(x, y) ≼ d(x, z) + d(z, y) for all x, y, z ∈ X.
Then, d is called a cone metric on X, and (X, d) is called a cone metric space.
Definition 3. [7]. Let (X, d) be a cone metric space, {x n } a sequence in X and x ∈ X. For every c ∈ E with c ≫ 0 E , we say that {x n } is
(C1) a Cauchy sequence if there is some k ∈ ℕ such that, for all n, m ≥ k, d(x n , x m ) ≪ c,
(C2) a convergent sequence if there is some k ∈ ℕ such that, for all n ≥ k, d(x n , x) ≪ c. Then x is called limit of the sequence {x n }.
Note that every convergent sequence in a cone metric space X is a Cauchy sequence. A cone metric space X is said to be complete if every Cauchy sequence in X is convergent in X.
Recently, Abbas et al. [8] introduced the concept of w-compatible mappings and established coupled coincidence point and coupled point of coincidence theorems for mappings satisfying a contractive condition in cone metric spaces.
In this paper, we introduce the concepts of  -compatible mappings, b-coupled coincidence point and b-common coupled fixed point for mappings F, G : X × X → X, where (X, d) is a cone metric space. We establish b-coupled coincidence and b-common coupled fixed point theorems in such spaces. The presented theorems generalize and extend several well-known comparable results in the literature, in particular the recent results of Abbas et al. [8] and the result of Olaleru [13]. Some examples and an application to non-linear integral equations are also considered.
-compatible mappings, b-coupled coincidence point and b-common coupled fixed point for mappings F, G : X × X → X, where (X, d) is a cone metric space. We establish b-coupled coincidence and b-common coupled fixed point theorems in such spaces. The presented theorems generalize and extend several well-known comparable results in the literature, in particular the recent results of Abbas et al. [8] and the result of Olaleru [13]. Some examples and an application to non-linear integral equations are also considered.
2 Main results
We start by recalling some definitions.
Definition 4. [16]. An element (x, y) ∈ X × X is called a coupled fixed point of mapping F : X × X → X if x = F(x, y) and y = F(y, x).
Definition 5. [17]. An element (x, y) ∈ X × X is called
-
(i)
a coupled coincidence point of mappings F : X × X → X and g : X → X if gx = F(x, y) and gy = F(y, x), and (gx, gy) is called coupled point of coincidence,
-
(ii)
a common coupled fixed point of mappings F : X × X → X and g : X → X if x = gx = F(x, y) and y = gy = F(y, x).
Note that if g is the identity mapping, then Definition 5 reduces to Definition 4.
Definition 6. [8]. The mappings F : X × X → X and g : X → X are called w-compatible if g(F(x, y)) = F(gx, gy) whenever gx = F(x, y) and gy = F(y, x).
Now, we introduce the following definitions.
Definition 7. An element (x, y) ∈ X × X is called
-
(i)
a b-coupled coincidence point of mappings F, G : X × X → X if G(x, y) = F(x, y) and G(y, x) = F(y, x), and (G(x, y), G(y, x)) is called b-coupled point of coincidence,
-
(ii)
a b-common coupled fixed point of mappings F, G : X × X → X if x = G(x, y) = F(x, y) and y = G(y, x) = F(y, x).
Example 1. Let × = ℝ and F, G : X × X → X the mappings defined by

for all x, y ∈ X. Then, (π/2, 0) is a b-coupled coincidence point of F and G, and (1, 0) is a b-coupled point of coincidence.
Example 2. Let X = ℝ and F, G : X × X → X the mappings defined by

for all x, y ∈ X. Then, (1, 2) is a b-common coupled fixed point of F and G.
Definition 8. The mappings F, G : X × X → X are called  -compatible if
-compatible if

whenever F(x, y) = G(x, y) and F(y, x) = G(y, x).
Example 3. Let X = ℝ and F, G : X × X → X the mappings defined by

for all x, y ∈ X. One can show easily that (x, y) is a b-coupled coincidence point of F and G if and only if x = y. Moreover, we have F(G(x, x), G(x, x)) = G(F(x, x), F(x, x)) for all x ∈ X. Then, F and G are -compatible.
-compatible.
If (X, d) is a cone metric space, we endow the product set X × X by the cone metric ν defined by

Now, we prove our first result.
Theorem 1. Let (X, d) be a cone metric space with a cone P having non-empty interior. Let F, G : X × X → X be mappings satisfying
(h1) for any (x, y) ∈ X × X, there exists (u, v) ∈ X × X such that F(x, y) = G(u, v) and F(y, x) = G(v, u),
(h2) {(G(x, y), G(y, x)): x, y ∈ X} is a complete subspace of (X × X, ν),
(h3) for any x, y, u, v ∈ X,

where a
i
, i = 1, ..., 10 are nonnegative real numbers such that  . Then F and G have a b-coupled coincidence point (x, y) ∈ X × X, that is, F(x, y) = G(x, y) and F(y, x) = G(y, x).
. Then F and G have a b-coupled coincidence point (x, y) ∈ X × X, that is, F(x, y) = G(x, y) and F(y, x) = G(y, x).
Proof. Let x0 and y0 be two arbitrary points in X. By (h1), there exists (x1, y1) such that

Continuing this process, we can construct two sequences {x n } and {y n } in X such that

For any n ∈ ℕ, let z n ∈ X and t n ∈ X as follows

Now, taking (x, y) = (x n , y n ) and (u, v) = (xn+1, yn+1) in the considered contractive condition and using (2), we have

Then, using the triangular inequality, one can write for any n ∈ ℕ*

Therefore,

Similarly, taking (x, y) = (y n , x n ) and (u, v) = (yn+1, xn+1) and reasoning as above, we obtain

Adding (4) to (5), we have

Let us denote

then, we deduce that

On the other hand, we have

from which by the triangular inequality, it follows that

Therefore,

Similarly, we find

Summing (8) to (9) and referring to (6), we get

Finally, from (7) and (10), we have for any n ∈ ℕ*

that is

where

Consequently, we have

If δ0 = 0 E , we get d(z0, z1) + d(t0, t1) = 0 E , that is, z0 = z1 and t0 = t1. Therefore, from (2) and (6), we have

and

meaning that (x1, y1) is a b-coupled coincidence point of F and G.
Now, assume that δ0 ≻ 0 E . If m > n, we have

Summing the two above inequalities, we obtain using also (13) and (6)

As  , we have 0 ≤ α < 1. Hence, for any c ∈ E with c ≫ 0
E
, there exists N ∈ ℕ such that for any n ≥ N, we have
, we have 0 ≤ α < 1. Hence, for any c ∈ E with c ≫ 0
E
, there exists N ∈ ℕ such that for any n ≥ N, we have  . Furthermore, for any m > n ≥ N, we get
. Furthermore, for any m > n ≥ N, we get

Thus, we proved that for any c ≫ 0 E , there exists n ∈ ℕ such that

This implies that {(z
n
, t
n
)} is a Cauchy sequence in the cone metric space (X × X, ν). On the other hand, we have (z
n
, t
n
) = (G(xn+1, yn+1), G(yn+1, xn+1)) ∈ {(G(x, y), G(y, x)): x, y ∈ X} that is a complete subspace of (X × X, ν) (from (h2)). Hence, there exists (z, t) ∈ {(G(x, y), G(y, x)): x, y ∈ X} such that for all c ≫ 0
E
, there exists  such that
such that

This implies that there exist x, y ∈ X such that z = G(x, y) and t = G(y, x) with

and

Now, we prove that F(x, y) = G(x, y) and F(y, x) = G(y, x), that is, (x, y) is a b-coupled coincidence point of F and G. First, by the triangular inequality, we have

On the other hand, applying the contractive condition in (h3), we get

Combining the above inequality with (16), and using again the triangular inequality, we get

Therefore, we have

Similarly, one can find

Summing (17) and (18), we get

Therefore, we have

where

From (13), (14) and (15), for any c ≫ 0 E , there exists N ∈ ℕ such that

for all n ≥ N. Thus, for all n ≥ N, we have

It follows that d(F(x, y), G(x, y)) = d(F(y, x), G(y, x)) = 0 E , that is, F(x, y) = G(x, y) and F(y, x) = G(y, x). Then, we proved that (x, y) is a b-coupled coincidence point of the mappings F and G. □
As consequences of Theorem 1, we give the following corollaries.
Corollary 1. Let (X, d) be a cone metric space with a cone P having non-empty interior. Let F, G : X × X → X be mappings satisfying
(h1) for any (x, y) ∈ X × X, there exists (u, v) ∈ X × X such that F(x, y) = G(u, v) and F(y, x) = G(v, u),
(h2) {(G(x, y), G(y, x)): x, y ∈ X} is a complete subspace of (X × X, ν),
(h3) for any x, y, u, v ∈ X,

where α
i
, i = 1, ..., 5 are nonnegative real numbers such that  . Then F and G have a b-coupled coincidence point (x, y) ∈ X × X, that is, F(x, y) = G(x, y) and F(y, x) = G(y, x).
. Then F and G have a b-coupled coincidence point (x, y) ∈ X × X, that is, F(x, y) = G(x, y) and F(y, x) = G(y, x).
Corollary 2. Let (X, d) be a cone metric space with a cone P having non-empty interior, F : X × X → X and g : X → X be mappings satisfying

for all x, y, u, v ∈ X, where a
i
, i = 1, ..., 10 are nonnegative real numbers such that  . If F(X × X) ⊆ g(X) and g(X) is a complete subset of X, then F and g have a coupled coincidence point in X, that is, there exists (x, y) ∈ X × X such that gx = F(x, y) and gy = F(y, x).
. If F(X × X) ⊆ g(X) and g(X) is a complete subset of X, then F and g have a coupled coincidence point in X, that is, there exists (x, y) ∈ X × X such that gx = F(x, y) and gy = F(y, x).
Proof. Consider the mapping G : X × X → X defined by

We will check that all the hypotheses of Theorem 1 are satisfied.
-
Hypothesis (h1):
Let (x, y) ∈ X × X. Since F(X × X) ⊆ g(X), there exists u ∈ X such that F(x, y) = gu = G(u, v) for any v ∈ X. Then, (h1) is satisfied.
-
Hypothesis (h2):
Let {x n } and {y n } be two sequences in X such that {(G(x n , y n ), G(y n , x n ))} is a Cauchy sequence in (X × X, ν). Then, for every c ≫ 0 E , there exists N ∈ ℕ such that

that is,

This implies that {gx n } and {gy n } are Cauchy sequences in (g(X), d). Since g(X) is complete, there exist x, y ∈ X such that

that is,

Therefore,

Then, {(G(x, y), G(y, x)): x, y ∈ X} is a complete subspace of (X × X, ν), and so the hypothesis (h2) is satisfied.
-
Hypothesis (h3):
The hypothesis (h3) follows immediately from (19).
Now, all the hypotheses of Theorem 1 are satisfied. Then, F and G have a b-coupled coincidence point (x, y) ∈ X × X, that is, F(x, y) = G(x, y) = gx and F(y, x) = G(y, x) = gy. Thus, (x, y) is a coupled coincidence point of F and g □
Corollary 3. Let (X, d) be a cone metric space with a cone P having non-empty interior, F : X × X → X and g : X → X be mappings satisfying

for all x, y, u, v ∈ X, where α
i
, i = 1, ..., 5 are nonnegative real numbers such that  . If F(X × X) ⊆ g(X) and g(X) is a complete subset of X, then F and g have a coupled coincidence point in X, that is, there exists (x, y) ∈ X × X such that gx = F(x, y) and gy = F(y, x).
. If F(X × X) ⊆ g(X) and g(X) is a complete subset of X, then F and g have a coupled coincidence point in X, that is, there exists (x, y) ∈ X × X such that gx = F(x, y) and gy = F(y, x).
Remark 1.
-
Putting a2 = a4 = a6 = a8 = 0 in Corollary 2, we obtain Theorem 2.4 of Abbas et al. [8];
-
Putting α2 = α4 = 0 in Corollary 3, we obtain Corollary 2.5 of [8].
Now, we are ready to state and prove a result of b-common coupled fixed point.
Theorem 2. Let F, G : X × X → X be two mappings which satisfy all the conditions of Theorem 1. If F and G are  -compatible, then F and G have a unique b-common coupled fixed point. Moreover, the b-common coupled fixed point of F and G is of the form (u, u) for some u ∈ X.
-compatible, then F and G have a unique b-common coupled fixed point. Moreover, the b-common coupled fixed point of F and G is of the form (u, u) for some u ∈ X.
Proof. First, we'll show that the b-coupled point of coincidence is unique. Suppose that (x, y) and (x*, y*) ∈ X × X with G(x, y) = F(x, y), G(y, x) = F(y, x), F(x*, y*) = G(x*, y*) and F(y*, x*) = G(y*, x*). Using (h3), we get

Similarly, we obtain

Therefore, summing the two previous inequalities, we get

Since a5 + a6 + a7 + a8 + a9 + a10 < 1, we obtain

which implies that

meaning the uniqueness of the b-coupled point of coincidence of F and G, that is, (G(x, y), G(y, x)).
Again, using (h3), we have

Similarly,

A summation gives

The fact that a5 + a6 + a7 + a8 + a9 + a10 < 1 yields that

In view of (20) and (21), one can assert that

This means that the unique b-coupled point of coincidence of F and G is (G(x, y), G(x, y)).
Now, let u = G(x, y), then we have u = G(x, y) = F(x, y) = G(y, x) = F(y, x). Since F and G are  -compatible, we have
-compatible, we have

that is, thanks to (22)

Consequently, (u, u) is a b-coupled coincidence point of F and G, and so (G(u, u), G(u, u)) is a b-coupled point of coincidence of F and G, and by its uniqueness, we get G(u, u) = G(x, y). Thus, we obtain

Hence, (u, u) is the unique b-common coupled fixed point of F and G. This makes end to the proof. □
Corollary 4. Let F : X × X → X and g : X → X be two mappings which satisfy all the conditions of Corollary 2. If F and g are w-compatible, then F and g have a unique common coupled fixed point. Moreover, the common fixed point of F and g is of the form (u, u) for some u ∈ X.
Proof. From the proof of Corollary 2 and the result given by Theorem 2, we have only to show that F and G are  -compatible, where G : X × X → X is defined by G(x, y) = gx for all x, y ∈ X. Let (x, y) ∈ X × X such that F(x, y) = G(x, y) and F(y, x) = G(y, x). From the definition of G, we get F(x, y) = gx and F(y, x) = gy. Since F and g are w-compatible, this implies that
-compatible, where G : X × X → X is defined by G(x, y) = gx for all x, y ∈ X. Let (x, y) ∈ X × X such that F(x, y) = G(x, y) and F(y, x) = G(y, x). From the definition of G, we get F(x, y) = gx and F(y, x) = gy. Since F and g are w-compatible, this implies that

Using (23), we have

Thus, we proved that F and G are  -compatible mappings, and the desired result follows immediately from Theorem 2. □
-compatible mappings, and the desired result follows immediately from Theorem 2. □
Remark 2. Corollary 4 generalizes Theorem 2.11 of [8].
Corollary 5. [13]. Let (X, d) be a cone metric space and f, g : X → X be mappings such that

for all x, u ∈ X, where α
i
∈ [0, 1), i = 1, ..., 5 and  . Suppose that f and g are weakly compatible, f(X) ⊆ g(X) and g(X) is a complete subspace of X. Then the mappings f and g have a unique common fixed point.
. Suppose that f and g are weakly compatible, f(X) ⊆ g(X) and g(X) is a complete subspace of X. Then the mappings f and g have a unique common fixed point.
Proof. Consider the mappings F, G : X × X → X defined by F(x, y) = fx and G(x, y) = gx for all x, y ∈ X. Then, the contractive condition (24) implies that

Then, F and G satisfy the hypothesis (h 3) of Theorem 1. Clearly, hypothesis (h 1) of Theorem 1 is satisfied since f(X) ⊆ g(X). The hypothesis (h 2) is also satisfied since g(X) is a complete subspace of X.
Now, we will show that F and G are  -compatible mappings. Let (x, y) ∈ X × X such that F(x, y) = G(x, y) and F(y, x) = G(y, x). This implies that fx = gx. Since f and g are weakly compatible, we have f(gx) = g(fx). Then, we have
-compatible mappings. Let (x, y) ∈ X × X such that F(x, y) = G(x, y) and F(y, x) = G(y, x). This implies that fx = gx. Since f and g are weakly compatible, we have f(gx) = g(fx). Then, we have

Thus, we proved that F and G are  -compatible mappings. Therefore, from Theorem 2, F and G have a unique b-common coupled fixed point (u, u) ∈ X × X such that u = F(u, u) = G(u, u), that is, u = fu = gu. This makes end to the proof. □
-compatible mappings. Therefore, from Theorem 2, F and G have a unique b-common coupled fixed point (u, u) ∈ X × X such that u = F(u, u) = G(u, u), that is, u = fu = gu. This makes end to the proof. □
Now, we give an example to illustrate our obtained results.
Example 4. Let X = [0, 1] endowed with the standard metric d(x, y) = |x - y| for all x, y ∈ X. Define the mappings G, F : X × X → X by

We will check that all the hypotheses of Theorem 1 are satisfied.
-
Hypothesis (h 1):
Let us prove that for any x, y ∈ X, there exist u, v ∈ X such that

Let (x, y) ∈ X × X be fixed. We consider the following cases.
Case-1: x = y.
In this case, F(x, y) = 0 = G(x, y) and F(y, x) = 0 = G(y, x).
Case-2: x > y.
In this case, we have

Case-3: x < y.
In this case, we have

Thus, we proved that (h 1) is satisfied.
-
Hypothesis (h 2):
Let us prove that Λ := {(G(x, y), G(y, x)): x, y ∈ [0, 1]} is a complete subspace of ([0, 1] × [0, 1], ν). Define the function φ : [0, 1] × [0, 1] → ℝ2by

Since φ is continuous and [0, 1] is compact, then Λ = φ([0, 1] × [0, 1]) is compact. On the other hand, ([0, 1] × [0, 1], ν) is complete. Then, we deduce that Λ is complete.
-
Hypothesis (h 3):
For all x, y, u, v ∈ X, we have

Then, (h 3) is satisfied with a1 = a2 = ⋯ = a8 = a10 = 0 and a9 = 1/3.
All the required hypotheses of Theorem 1 are satisfied. Consequently, F and G have a b-coupled coincidence point.
In this case, for any x, y ∈ [0, 1], (x, y) is a b-coupled coincidence point if and only if x = y. Moreover, we have

This implies that F and G are -compatible. Applying our Theorem 2, we obtain the existence and uniqueness of b-common coupled fixed point of F and G. In this example, (0, 0) is the unique b-common coupled fixed point.
-compatible. Applying our Theorem 2, we obtain the existence and uniqueness of b-common coupled fixed point of F and G. In this example, (0, 0) is the unique b-common coupled fixed point.
3 Application
In this section, we study the existence of solutions of a system of nonlinear integral equations using the results proved in Section 2.
Consider the following system of integral equations:


where t ∈ [0, T], T > 0.
Let X = C([0, T], ℝ) be the set of continuous functions defined on [0, T] endowed with the metric given by

We consider the following assumptions:
-
(a)
k : [0, T] × [0, T] → ℝ is a continuous function,
-
(b)
a ∈ C([0, T], ℝ),
-
(c)
f : [0, T] × ℝ × ℝ → ℝ is a continuous function,
-
(d)
G : C([0, T], ℝ) × C([0, T], ℝ) → C([0, T], ℝ) is a mapping satisfying:
(d.1) For all x, y ∈ C([0, T], ℝ), there exist u, v ∈ C([0, T], ℝ) such that

for all t ∈ [0, T],
(d.2) The set {(G(x, y), G(y, x)): x, y ∈ C([0, T], ℝ)} is closed,
-
(e)
For all t ∈ [0, T], for all x, y, u, v ∈ X, we have
-
(f)
 .
.
Now, we formulate our result.
Theorem 3. Under hypotheses (a) - (f), system (25)-(26) has at least one solution in C([0, T], ℝ).
Proof. We consider the operator F : X × X → X defined by

It is easy to show that (x, y) is a solution to (25)-(26) if and only if (x, y) is a b-coupled coincidence point of F and G. To establish the existence of such a point, we will use our Theorem 1. Then, we have to check that all the hypotheses of Theorem 1 are satisfied.
-
Hypotheses (h1)-(h2) follow immediately from assumption (d).
-
Hypothesis (h3): Let x, y, u, v ∈ X. For all t ∈ [0, T], we have
Using condition (e), we get

Using condition (f), we obtain

This implies that

for all x, y, u, v ∈ X. Then, hypothesis (h3) is satisfied with a9 = MT < 1 (from condition (f)) and a1 = a2 = ⋯ = a8 = a10 = 0.
Now, applying Theorem 2, we obtain the existence of a solution to system (25)-(26). □
References
Kantorovich LV: The majorant principle and Newton's method. Dokl Akad Nauk SSSR (NS) 1951, 76: 17–20.
Kantorovich LV: On some further applications of the Newton approximation method. Vestn Leningr Univ Ser Mat Mekh Astron 1957, 12: 68–103.
Vandergraft JS: Newton's method for convex operators in partially ordered spaces. SIAM J Numer Anal 1967, 4: 406–432. 10.1137/0704037
Zabreǐko PP: K-metric and K-normed spaces: survey. Collect Math 1997, 48: 825–859.
Deimling K: Nonlinear Functional Analysis. Springer; 1985.
Aliprantis CD, Tourky R: Cones and duality. Graduate Studies in Mathematics, American Mathematical Society, Providence, RI 2007., 84:
Huang LG, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. J Math Anal Appl 2007, 332: 1467–1475.
Abbas M, Ali Khan M, Radenović S: Common coupled fixed point theorems in cone metric spaces for w -compatible mappings. Appl Math Comput 2010, 217: 195–202. 10.1016/j.amc.2010.05.042
Altun I, Damjanović B, Djorić D: Fixed point and common fixed point theorems on ordered cone metric spaces. Appl Math Lett 2010, 23: 310–316. 10.1016/j.aml.2009.09.016
Beg I, Azam A, Arshad M: Common fixed points for maps on topological vector space valued cone metric spaces. Int J Math Math Sci 2009, 2009: 8. Article ID560264
Di Bari C, Vetro P: φ -pairs and common fixed points in cone metric spaces. Rend Cir Mat Palermo 2008, 57: 279–285. 10.1007/s12215-008-0020-9
Di Bari C, Vetro P: Weakly φ -pairs and common fixed points in cone metric spaces. Rend Cir Mat Palermo 2009, 58: 125–132. 10.1007/s12215-009-0012-4
Olaleru JO: Some generalizations of fixed point theorems in cone metric spaces. Fixed Point Theory Appl 2009, 2009: 10. Article ID 657914
Rezapour Sh, Hamlbarani R: Some notes on the paper "Cone metric spaces and fixed point theorems of contractive mappings". J Math Anal Appl 2008, 345: 719–724. 10.1016/j.jmaa.2008.04.049
Vetro P: Common fixed points in cone metric spaces. Rend Circ Mat Palermo 2007, 56: 464–468. 10.1007/BF03032097
Bhashkar TG, Lakshmikantham V: Fixed point theorems in partially ordered cone metric spaces and applications. Nonlinear Anal 2006, 65: 825–832. 10.1016/j.na.2005.10.015
Lakshmikantham V, Ćirić L: Coupled fixed point theorems for nonlinear contractions in partially ordered metric spaces. Nonlinear Anal 2009, 70: 4341–4349. 10.1016/j.na.2008.09.020
Acknowledgements
Calogero Vetro was supported by Università degli Studi di Palermo, Local University Project R. S. ex 60%.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
All authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Aydi, H., Samet, B. & Vetro, C. Coupled fixed point results in cone metric spaces for  -compatible mappings.
Fixed Point Theory Appl 2011, 27 (2011). https://doi.org/10.1186/1687-1812-2011-27
-compatible mappings.
Fixed Point Theory Appl 2011, 27 (2011). https://doi.org/10.1186/1687-1812-2011-27
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-27
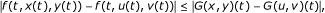
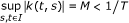 .
.