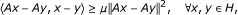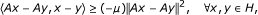- Research
- Open access
- Published:
Systems of general nonlinear set-valued mixed variational inequalities problems in Hilbert spaces
Fixed Point Theory and Applications volume 2011, Article number: 31 (2011)
Abstract
In this paper, the existing theorems and methods for finding solutions of systems of general nonlinear set-valued mixed variational inequalities problems in Hilbert spaces are studied. To overcome the difficulties, due to the presence of a proper convex lower semi-continuous function, φ and a mapping g, which appeared in the considered problem, we have used some applications of the resolvent operator technique. We would like to point out that although many authors have proved results for finding solutions of the systems of nonlinear set-valued (mixed) variational inequalities problems, it is clear that it cannot be directly applied to the problems that we have considered in this paper because of φ and g.
2000 AMS Subject Classification: 47H05; 47H09; 47J25; 65J15.
1. Introduction and preliminaries
Let H be a real Hilbert space, whose inner product and norm are denoted by 〈·, ·〉, and ||·||, respectively. Let CB(H) be the family of all nonempty, closed, and bounded sets in H. Let A, B : H → CB(H) be nonlinear set-valued mappings, g : H → H be a single-valued mapping, and φ : H → (-∞, +∞] be a proper convex lower semi-continuous function on H. For each fixed positive real numbers, ρ and η, we consider the following so-called system of general nonlinear set-valued mixed variational inequalities problems:
Find x*, y*∈ H, u* ∈ Ay*, v* ∈ Bx*, such that

We denote by SGNSM(A, B, g, φ, ρ, η), the set of all solutions (x*, y*, u*, v*) of the problem (1.1).
We shall now discuss several special cases of the problem (1.1).
Special cases of the problem (1.1) are as follows:
-
(I)
If g = I (: the identity operator), then, from the problem (1.1), we have the following system of nonlinear set-valued mixed variational inequalities problems:
Find x*, y* ∈ H, u* ∈ Ay*, v* ∈ Bx*, such that

We denote by SNSM(A, B, φ, ρ, η), the set of all solutions (x*, y*, u*, v*) of the problem (1.2).
-
(II)
If K is a closed convex subset of H and φ (x) = δ K (x) for all x ∈ K, where δ K is the indicator function of K defined by
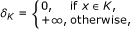
then, from the problem (1.1), we have the following system of general nonlinear set-valued variational inequalities problems:
Find x*, y* ∈ K, u* ∈ Ay*, v* ∈ Bx*, such that

We denote by SGNS(A, B, g, K, ρ, η), the set of all solutions (x*, y*, u*, v*) of the problem (1.3).
The problem (1.3) was recently introduced and studied by Noor [1], when A and B are single-valued mappings. Consequently, it was pointed out that such a problem includes a wide class of the system of variational inequalities problems and related optimization problems as special cases, and hence the results announced in [1] is very interesting.
-
(III)
If A, B : H → H are single-valued mappings, then, from the problem (1.1), we have the following system of general nonlinear mixed variational inequalities problems:
Find x*, y* ∈ H, such that

We denote by SGNM(A, B, g, φ, ρ, η), the set of all solutions (x*, y*) of the problem (1.4).
This means, generally speaking, the class of system general nonlinear set-valued variational inequalities problems is more general and has had a great impact and influence in the development of several branches of pure, applied, and engineering sciences. For more information and results on the general variational inequalities problems, one may consult [2–18].
Inspired and motivated by the recent research going on in this area, in this paper, we consider the existence theorem and a method for finding solutions for the systems of nonlinear general set-valued mixed variational inequalities problems (1.1). Our results extend the results announced by Noor [1], from single-valued mappings to set-valued mappings, and hence include several related problems as spacial cases.
We need the following basic concepts and well-known results:
Definition 1.1. A mapping g : H → H is said to be:
-
(1)
monotone if

-
(2)
ν-strongly monotone if there exists a constant ν > 0, such that

Definition 1.2. A set-valued mapping A : H → 2 H is said to be ν-strongly monotone if there exists a constant ν > 0, such that,

Definition 1.3. A set-valued mapping A : H → CB(H) is said to be τ-Lipschitzian continuous if there exists a constant τ > 0, such that,

where H(·,·) is the Hausdorff metric on CB(H).
Definition 1.4. A single-valued mapping T : H → H is said to be a κ-Lipschitzian continuous mapping if there exists a positive constant κ, such that,

In the case of κ = 1, the mapping T is known as a nonexpansive mapping.
Definition 1.5. [19] If M is a maximal monotone operator on H, then, for any λ > 0, the resolvent operator associated with M is defined as

It is well-known that a monotone operator is maximal if and only if its resolvent operator is defined everywhere. Furthermore, the resolvent operator is single-valued and nonexpansive. In particular, it is well-known that the subdifferential ∂φ of a proper convex lower semi-continuous function φ : H → (-∞, +∞] is a maximal monotone operator.
Moreover, we have the following interesting characterization:
Lemma 1.6. [19]The points u, z ∈ H satisfy the inequality

if and only if u = J φ (z), where J φ (I + λ∂φ)-1is the resolvent operator and λ > 0 is a constant.
The property of the resolvent operator J φ presented in Lemma 1.6 plays an important role in developing the numerical methods for solving the system of general nonlinear set-valued mixed variational inequalities problems. In fact, assuming that g : H → H is a surjective mapping and by applying Lemma 1.6, one can easily prove the following result:
Lemma 1.7. If g : H → H is a surjective mapping, then the problem (1.1) is equivalent to the following problem:
Find x*, y* ∈ H, u* ∈ Ay*, v* ∈ Bx*, such that,

where J φ = (I + ∂φ)-1.
The equivalent formulation (1.5) enables us to suggest an explicit iterative method for solving the system of general nonlinear set-valued mixed variational inequalities problem (1.1), as we show in the next section. Of course, we hope to use the Lemma 1.7 to obtain our results in this paper, and hence, from now on, we assume that the mapping g : H → H is a surjection.
In order to prove our main results, the next lemma is very important.
Lemma 1.8. [20]Let B1, B2 ∈ CB(H) and r > 1 be any real number. Then, for all b1 ∈ B1, there exists b2 ∈ B2, such that ||b1 - b2|| ≤ rH(B1, B2).
2. Main results
We begin with some observations that are guidelines to a method for proving the main results in this paper.
Remark 2.1. If (x*, y*, u*, v*) ∈ SGNSM(A, B, g, φ, ρ, η), then it follows from (1.5) that

From Remark 2.1, we suggest a method for finding a solution for the problem (2.1), as following iterative procedures:
Let {ε n } be a sequence of positive real numbers with ε n → 0 as n → ∞ and t ∈ (0, 1] be fixed. For any x0, y0 ∈ H, pick u0 ∈ Ay0 and let

Then take v1 ∈ Bx1 and let

Now, by Lemma 1.8, there exists u1 ∈Ay1, such that

Take

Similarly, by Lemma 1.8, there exists v2 ∈ Bx2, such that

Take

Inductively, we have the following algorithm:
Algorithm 1. Let {ε
n
} be a sequence of nonnegative real numbers with ε
n
→ 0 as n → ∞ and t ∈ (0, 1] be a fixed constant. For any x0, y0 ∈ H, compute the sequences {x
n
}, {y
n
} ⊂ H,  and
and  generated by the iterative processes:
generated by the iterative processes:

We now state and prove the existence theorem of a solution for the problem (1.1).
Theorem 2.2. Let H be a real Hilbert space. Let A : H → CB(H) be ν A -strongly monotone and Lipschitz continuous mapping with a constant τ A and B : H → CB(H) be ν B -strongly monotone and Lipschitz continuous mapping with a constant τ B . Let g : H → H be ν g -strongly monotone and Lipschitz continuous mapping with a constant τ g . Put

If the following conditions are satisfied:
-
(i)
p ∈ [0, δ ), where
 ,
, -
(ii)
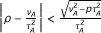 and
and 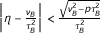 ,
,
then SGNSM(A, B, g, φ, ρ, η) ≠ ∅. Moreover, the sequence {x n }, {y n }, {u n }, and {v n } defined by (2.1) converge strongly to x*, y*, u*, and v*, respectively, where (x*, y*, u*, v*) ∈ SGNSM(A, B, g, φ, ρ, η).
Proof. Firstly, by (2.1), we have

Now, we compute

and

where  . Substituting (2.3) and (2.4) into (2.2), we have
. Substituting (2.3) and (2.4) into (2.2), we have

Now, since yn+1= J φ [g(xn+1) - ηvn+1] and the resolvent operator J φ is nonexpansive, we have

Using the same lines as in (2.3) and (2.4), we know that

where  . Substituting (2.6) into (2.5), we have
. Substituting (2.6) into (2.5), we have

Observe that

and

Consequently, by the conditions (i) and (ii), we have Δ =: (p + q)(p + r) < 1.
Now, let s ∈ (Δ, 1) be a fixed real number. Then, by (2.8) and (2.9), there exists a positive integer, N, such that (p + q n )(p + r n ) < s for all n ≥ N. Then, by (2.7), we have

where κ : = 1 - t(1 - s). Then it follows from (2.10) that

Hence it follows that

Since κ < 1, it follows from (2.11) that ||x m - x n || → 0 as n → ∞, which implies that {x n } is a Cauchy sequence in H. Consequently, by (2.6), it follows that {y n } is a Cauchy sequence in H. Moreover, since A is a τ A - Lipschitz continuous mapping, and B is a τ B -Lipschitz continuous mapping, we also know that {u n } and {v n } are Cauchy sequences, respectively. Thus there exist x*, y*, u*, v* ∈ H, such that x n → x*, y n → y*, u n → u*, and v n → v* as n → ∞. Moreover, by applying the continuity of the mappings A, B, g, and J φ to (2.1), we have

Hence, from Lemma 1.7, it follows that (x*, y*, u*, v*) ∈ SGNSM(A, B, g, φ, ρ, η).
Finally, we prove that u* ∈ Ay* and v* ∈ Bx*. Indeed, we have

That is, d(u*, Ay*) = 0. Hence, since Ay* ∈ CB(H), we must have u* ∈ Ay*.
Similarly, we can show that v* ∈ Bx*. This completes the proof.
Remark 2.3. Theorem 2.2 not only gives the conditions for the existence of a solution for the problem (1.1) but also provides an iterative algorithm to find such a solution for any initial points x0, y0 ∈ H.
Using Theorem 2.2, we can obtain the following results:
-
(I)
If g = I (: the identity mapping), then from Algorithm 1, we have the following:
Algorithm 2. Let {ε
n
} be a sequence of nonnegative real numbers with ε
n
→ 0. Let t ∈ (0, 1] be a fixed constant. For any x0, y0 ∈ H, compute the sequences {x
n
}, {y
n
} ⊂ H,  and
and  generated by the iterative processes:
generated by the iterative processes:

where u n ∈ Ay n and v n ∈ Bx n satisfy the following:

Corollary 2.4. Let H be a real Hilbert space. Let A : H → CB(H) be ν A -strongly monotone and Lipschitz continuous mapping with a constant τ A , and B : H → CB(H) be ν B -strongly monotone and Lipschitz continuous mapping with a constant τ B . If

then SNSM(A, B, φ, ρ, η) ≠ ∅. Moreover, the sequences {x n }, {y n }, {u n }, and {v n } defined by (2.12) converge strongly to x*, y*, u* and v*, respectively, where (x*, y*, u*, v*) ∈ SNSM(A, B, φ, ρ, η).
Proof. If g = I (: the identity operator), we know that the constant p defined in Theorem 2.2 is vanished. Thus the result follows immediately.
-
(II)
If the function φ(·) is the indicator function of a closed convex set K in H, then it is well-known that J φ = P K , the projection operator of H onto the closed convex set K (see [2]). Then, from Algorithm 1, we have the following:
Algorithm 3. Let {ε
n
} be a sequence of nonnegative real numbers with ε
n
→ 0 as n → ∞. Let t ∈ (0, 1] be a fixed constant. For any x0, y0 ∈ K, compute the sequences {x
n
}, {y
n
} ⊂ K,  , and
, and  generated by the iterative processes:
generated by the iterative processes:

Corollary 2.5. Let K be a closed convex subset of a real Hilbert space H. Let A : K → CB(H) be ν A -strongly monotone and Lipschitz continuous mapping with a constant τ A , and B : K → CB(H) be ν B -strongly monotone and Lipschitz continuous mapping with a constant τ B . Let g : K → K be a ν g -strongly monotone and Lipschitz continuous mapping with a constant τ g and satisfying K ⊂ g(H).
Put

If the following conditions are satisfied:
-
(i)
p ∈ [0, δ), where
 ,
, -
(ii)
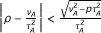 , and
, and 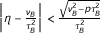 ,
,
then SGNS(A, B, g, K, ρ, η) ≠ ∅. Moreover, the sequence {x n }, {y n }, {u n }, and {v n } defined by (2.13) converge strongly to x*, y*, u* and v*, respectively, where (x*, y*, u*, v*) ∈ SGNS(A, B, g, K, ρ, η).
Remark 2.6. Corollary 2.5 is an extension of the results announced by Noor [1] from single-valued mappings to set-valued mappings.
-
(III)
If A, B : H → H are single-valued mappings, then, from Algorithm 1, we have the following:
Algorithm 4. Let t ∈ (0, 1] be a fixed constant. For any x0, y0 ∈ H, compute the sequences {x n }, {y n } ⊂ H by the iterative processes:

Corollary 2.7. Let H be a real Hilbert space. Let A : H → H be ν A -strongly monotone and Lipschitz continuous mapping with a constant τ A , and B : H → H be ν B -strongly monotone and Lipschitz continuous mapping with a constant τ B . Let g : H → H be ν g -strongly monotone and Lipschitz continuous mapping with a constant τ g . Put

If the following conditions are satisfied:
-
(i)
p ∈ [0, δ), where
 ,
, -
(ii)
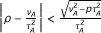 , and
, and 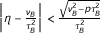 ,
,
then SGNM(A, B, g, φ, ρ, η) ≠ ∅. Moreover, the sequences {x n } and {y n } defined by (2.14) converge strongly to x* and y*, respectively, where (x*, y*) ∈ SGNM(A, B, g, φ, ρ, η).
Remark 2.8. Under the assumption of Corollary 2.7, the solution of SGNM(A, B, g, φ, ρ, η) is unique, that is, there is a unique (x*, y*) ∈ H×H such that (x*, y*) ∈ SGNM(A, B, g, φ, ρ, η). Indeed, if (x*, y*) and (x', y') are elements of SGNM(A, B, g, φ, ρ, η). Put

Replacing xn+1by x*, x n by x', y n by y*, and yn-1by y', then, following the lines proof given in Theorem 2.2, we know that

and

By the conditions (i), (ii), and (2.16), we must have x* = x'. Consequently, by (2.15), we also have y* = y'.
Remark 2.9. Recall that a mapping A : H → H is said to be:
-
(1)
μ-cocoercive if there exists a constant μ > 0 such that
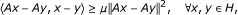
-
(2)
relaxed μ-cocoercive if there exists a constant μ > 0 such that
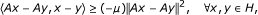
-
(3)
relaxed (μ, ν)-cocoercive if there exist constants μ, ν > 0 such that

It is easy to see that the class of the relaxed (μ, ν)- cocoercive mappings is the most general one. However, it is worth noting that if the mapping A is relaxed (μ, ν)-cocoercive, and τ-Lipschitz continuous mapping satisfying ν - μτ2> 0, then A is a (ν - μτ2)-strongly monotone. Hence, the result appeared in Corollary 2.7 can be also applied to the class of the relaxed cocoercive mappings. In the conclusion, for a suitable and appropriate choice of the mappings A, B, g, and φ, Theorem 2.2 includes many important known results given by some authors as special cases.
References
Noor MA: On a system of general mixed variational inequalities. Optim Lett 2009, 3: 437–451. 10.1007/s11590-009-0123-z
Baiocchi C, Capelo A: Variational and Quasi-Variational Inequalities. Wiely, New York; 1984.
Ceng LC, Wang CY, Yao JC: Strong convergence theorems by a relaxed extragradient method for a general system of variational inequalities. Math Methods Oper Res 2008, 67: 375–390. 10.1007/s00186-007-0207-4
Inchan I, Petrot N: System of general variational inequalities involving different nonlinear operators related to fixed point problems and its applications. Fixed Point Theory Appl 2011, 2011: Article ID 689478. 17
Nie NH, Liu Z, Kim KH, Kang SM: A system of nonlinear variational inequalities involving strong monotone and pseudocontractive mappings. Adv Nonlinear Var Inequal 2003, 6: 91–99.
Noor MA: General variational inequalities. Appl Math Lett 1988, 1: 119–121. 10.1016/0893-9659(88)90054-7
Noor MA: Some developments in general variational inequalities. Appl Math Comput 2004, 152: 199–277. 10.1016/S0096-3003(03)00558-7
Noor MA: Variational Inequalities and Applications. Lecture Notes, Mathematics Department, COMSATS Institute of Information Technology, Islamabad, Pakistan 2007.
Noor MA: On a class of general variational inequalities. J Adv Math Stud 2008, 1: 75–86.
Noor MA: Differentiable nonconvex functions and general variational inequalities. Appl Math Comput 2008, 199: 623–630. 10.1016/j.amc.2007.10.023
Noor MA: Extended general variational inequalities. Appl Math Lett 2009, 22: 182–186. 10.1016/j.aml.2008.03.007
Noor MA, Noor KI, Yaqoob H: On general mixed variational inequalities. Acta Appl Math 2008.
Petrot N: Existence and algorithm of solutions for general set-valued Noor variational inequalities with relaxed ( μ , ν )-cocoercive operators in Hilbert spaces. J Appl Math Comput 2010, 32: 393–404. 10.1007/s12190-009-0258-1
Verma RU: On a new system of nonlinear variational inequalities and associated iterative algorithms. Math Sci Res Hot-Line 1999, 3: 65–68.
Verma RU: A new class of iterative algorithms for approximation-solvability of nonlinear variational inequalities. Comput Math Appl 2001, 41: 505–512. 10.1016/S0898-1221(00)00292-3
Verma RU: Generalized system for relaxed variational inequalities and its projection methods. J Optim Theory Appl 2004, 121: 203–210.
Verma RU: Generalized class of partial relaxed monotonicity and its connections. Adv Nonlinear Var Inequal 2004, 7: 155–164.
Verma RU: General convergence analysis for two-step projection methods and applications to variational problems. Appl Math Lett 2005, 18: 1286–1292. 10.1016/j.aml.2005.02.026
Brezis H: Opérateurs maximaux monotone et semi-groupes de contractions dans les espaces de Hilbert, North-Holland Mathematics Studies, 5 Notas de matematica (50). North-Holland, Amsterdam; 1973.
Nadler SB Jr: Multi-valued contraction mappings. Pacific J Math 1969, 30: 475–487.
Acknowledgements
Yeol Je Cho was supported by the Korea Research Foundation Grant funded by the Korean Government (KRF-2008-313-C00050). Narin Petrot was supported by the Centre of Excellence in Mathematics, the commission on Higher Education, Thailand.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
Both authors contributed equally in this paper. They read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Agarwal, R.P., Cho, Y.J. & Petrot, N. Systems of general nonlinear set-valued mixed variational inequalities problems in Hilbert spaces. Fixed Point Theory Appl 2011, 31 (2011). https://doi.org/10.1186/1687-1812-2011-31
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-31
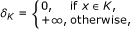


 ,
,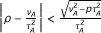 and
and 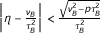 ,
,