- Research
- Open access
- Published:
A relaxed hybrid steepest descent method for common solutions of generalized mixed equilibrium problems and fixed point problems
Fixed Point Theory and Applications volume 2011, Article number: 32 (2011)
Abstract
In the setting of Hilbert spaces, we introduce a relaxed hybrid steepest descent method for finding a common element of the set of fixed points of a nonexpansive mapping, the set of solutions of a variational inequality for an inverse strongly monotone mapping and the set of solutions of generalized mixed equilibrium problems. We prove the strong convergence of the method to the unique solution of a suitable variational inequality. The results obtained in this article improve and extend the corresponding results.
AMS (2000) Subject Classification: 46C05; 47H09; 47H10.
1. Introduction
Let H be a real Hilbert space, C be a nonempty closed convex subset of H and let P C be the metric projection of H onto the closed convex subset C. Let S : C → C be a nonexpansive mapping, that is, ||Sx - Sy|| ≤ ||x - y|| for all x, y ∈ C. We denote by F(S) the set fixed point of S. If C ⊂ H is nonempty, bounded, closed and convex and S is a nonexpansive mapping of C into itself, then F(S) is nonempty; see, for example, [1, 2]. A mapping f : C → C is a contraction on C if there exists a constant η ∈ (0, 1) such that ||f(x) - f(y)|| ≤ η||x - y|| for all x, y ∈ C. In addition, let D : C → H be a nonlinear mapping, φ : C → ℝ ∪ {+∞} be a real-valued function and let F : C × C → ℝ be a bifunction such that C ∩ dom φ ≠ ∅, where ℝ is the set of real numbers and dom φ = {x ∈ C : φ(x) < +∞}.
The generalized mixed equilibrium problem for finding x ∈ C such that

The set of solutions of (1.1) is denoted by GMEP(F, φ, D), that is,

We find that if x is a solution of a problem (1.1), then x ∈ dom φ.
If D = 0, then the problem (1.1) is reduced into the mixed equilibrium problem which is denoted by MEP(F, φ).
If φ = 0, then the problem (1.1) is reduced into the generalized equilibrium problem which is denoted by GEP(F, D).
If D = 0 and φ = 0, then the problem (1.1) is reduced into the equilibrium problem which is denoted by EP(F).
If F = 0 and φ = 0, then the problem (1.1) is reduced into the variational inequality problem which is denoted by VI(C, D).
The generalized mixed equilibrium problems include, as special cases, some optimization problems, fixed point problems, variational inequality problems, Nash equilibrium problems in noncooperative games, equilibrium problem, Numerous problems in physics, economics and others. Some methods have been proposed to solve the problem (1.1); see, for instance, [3, 4] and the references therein.
Definition 1.1. Let B : C → H be nonlinear mappings. Then, B is called
-
(1)
monotone if 〈Bx - By, x - y〉 ≥ 0, ∀x, y ∈ C,
-
(2)
β-inverse-strongly monotone if there exists a constant β > 0 such that
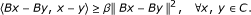
-
(3)
A set-valued mapping Q : H → 2 H is called monotone if for all x, y ∈ H, f ∈ Qx and g ∈ Qy imply 〈x- y, f - g〉 ≥ 0. A monotone mapping Q : H → 2 H is called maximal if the graph G(Q) of Q is not properly contained in the graph of any other monotone mapping. It is well known that a monotone mapping Q is maximal if and only if for (x, f) Î H × H, 〈x - y, f - g〉 ≥ 0 for every (y, g) Î G(Q) implies f Î Qx.
A typical problem is to minimize a quadratic function over the set of fixed points of a nonexpansive mapping defined on a real Hilbert space H:

where F is the fixed point set of a nonexpansive mapping S defined on H and b is a given point in H.
A linear-bounded operator A is strongly positive if there exists a constant  with the property
with the property

Recently, Marino and Xu [5] introduced a new iterative scheme by the viscosity approximation method:

They proved that the sequences {x n } generated by (1.2) converges strongly to the unique solution of the variational inequality

which is the optimality condition for the minimization problem:

where h is a potential function for γf.
For finding a common element of the set of fixed points of a nonexpansive mapping and the set of solutions of variational inequalities for a ξ-inverse-strongly monotone mapping, Takahashi and Toyoda [6] introduced the following iterative scheme:

where B is a ξ-inverse-strongly monotone mapping, {γ n } is a sequence in (0, 1), and {α n } is a sequence in (0, 2ξ). They showed that if F(S) ∩ VI(C, B) is nonempty, then the sequence {x n } generated by (1.3) converges weakly to some z ∈ F(S) ∩ VI(C, B).
The method of the steepest descent, also known as The Gradient Descent, is the simplest of the gradient methods. By means of simple optimization algorithm, this popular method can find the local minimum of a function. It is a method that is widely popular among mathematicians and physicists due to its easy concept.
For finding a common element of F(S) ∩ VI(C, B), let S : H → H be nonexpansive mappings, Yamada [7] introduced the following iterative scheme called the hybrid steepest descent method:

where x1 = x ∈ H, {α n } ⊂ (0, 1), B : H → H is a strongly monotone and Lipschitz continuous mapping and μ is a positive real number. He proved that the sequence {x n } generated by (1.4) converged strongly to the unique solution of the F(S) ∩ VI(C, B).
On the other hand, for finding an element of F(S) ∩ VI(C, B) ∩ EP(F), Su et al. [8] introduced the following iterative scheme by the viscosity approximation method in Hilbert spaces: x1 ∈ H

where α n ⊂ [0, 1) and r n ⊂ (0, ∞) satisfy some appropriate conditions. Furthermore, they prove {x n } and {u n } converge strongly to the same point z ∈ F(S) ∩ VI(C, B) ∩ EP(F), where z = PF(S)∩VI(C,B) ∩ EP(F)f(z).
For finding a common element of F(S) ∩ GEP(F, D), let C be a nonempty closed convex subset of a real Hilbert space H. Let D be a β-inverse-strongly monotone mapping of C into H, and let S be a nonexpansive mapping of C into itself, Takahashi and Takahashi [9] introduced the following iterative scheme:

where {α n } ⊂ [0, 1], {γ n } ⊂ [0, 1] and {r n } ⊂ [0, 2β] satisfy some parameters controlling conditions. They proved that the sequence {x n } defined by (1.6) converges strongly to a common element of F(S) ∩ GEP(F, D).
Recently, Chantarangsi et al. [10] introduced a new iterative algorithm using a viscosity hybrid steepest descent method for solving a common solution of a generalized mixed equilibrium problem, the set of fixed points of a nonexpansive mapping and the set of solutions of variational inequality problem in a real Hilbert space. Jaiboon [11] suggests and analyzes an iterative scheme based on the hybrid steepest descent method for finding a common element of the set of solutions of a system of equilibrium problems, the set of fixed points of a nonexpansive mapping and the set of solutions of the variational inequality problems for inverse strongly monotone mappings in Hilbert spaces.
In this article, motivated and inspired by the studies mentioned above, we introduce an iterative scheme using a relaxed hybrid steepest descent method for finding a common element of the set of solutions of generalized mixed equilibrium problems, the set of fixed points of a nonexpansive mapping and the set of solutions of variational inequality problems for inverse strongly monotone mapping in a real Hilbert space. Our results improve and extend the corresponding results of Jung [12] and some others.
2. Preliminaries
Throughout this article, we always assume H to be a real Hilbert space, and let C be a nonempty closed convex subset of H. For a sequence {x n }, the notation of x n ⇀ x and x n → x means that the sequence {x n } converges weakly and strongly to x, respectively.
For every point x ∈ H, there exists a unique nearest point in C, denoted by P C x, such that

Such a mapping P C from H onto C is called the metric projection.
The following known lemmas will be used in the proof of our main results.
Lemma 2.1. Let H be a real Hilbert spaces H. Then, the following identities hold:
-
(i)
for each x ∈ H and x* ∈ C, x* = P C x ⇔ 〈x - x*, y - x*〉 ≤ 0, ∀y ∈ C;
-
(ii)
P C : H → C is nonexpansive, that is, ||P C x - P C y|| ≤ ||x - y||, ∀x, y ∈ H;
-
(iii)
P C is firmly nonexpansive, that is, ||P C x - P C y||2 ≤ 〈P C x - P C y, x - y〉, ∀x, y ∈ H;
-
(iv)
||tx + (1 - t)y||2 = t||x||2 + (1 - t)||y||2 - t(1 - t)||x - y||2, ∀t ∈ [0, 1], ∀x, y ∈ H;
-
(v)
||x + y||2 ≤ ||x||2 + 2〈y, x + y〉.
Lemma 2.2. [2]Let H be a Hilbert space, let C be a nonempty closed convex subset of H, and let B be a mapping of C into H. Let x* ∈ C. Then, for λ > 0,

where P C is the metric projection of H onto C.
Lemma 2.3. [2]Let H be a Hilbert space, and let C be a nonempty closed convex subset of H. Let β > 0, and let A : C → H be β-inverse strongly monotone. If 0 < ϱ ≤ 2β, then I -ϱA is a nonexpansive mapping of C into H, where I is the identity mapping on H.
Lemma 2.4. Let H be a real Hilbert space, let C be a nonempty closed convex subset of H, let S : C → C be a nonexpansive mapping, and let B : C → H be a ξ-inverse strongly monotone. If 0 < α n ≤ 2ξ, then S - α n BS is a nonexpansive mapping in H.
Proof. For any x, y ∈ C and 0 < α n ≤ 2ξ, we have

Hence, S - α n BS is a nonexpansive mapping of C into H. □
Lemma 2.5. [13]Let B be a monotone mapping of C into H and let N C w1be the normal cone to C at w1 ∈ C, that is, N C w1 = {w ∈ H : 〈w1 - w2, w〉 ≥ 0, ∀w2 ∈ C} and define a mapping Q on C by

Then, Q is maximal monotone and 0 ∈ Qw1if and only if w1 ∈ VI(C, B).
Lemma 2.6. [14]Each Hilbert space H satisfies Opial's condition, that is, for any sequence {x n } ⊂ H with x n ⇀ x, the inequality

holds for each y ∈ H with y ≠ x.
Lemma 2.7. [5]Let C be a nonempty closed convex subset of H and let f be a contraction of H into itself with coefficient η ∈ (0, 1) and A be a strongly positive linear-bounded operator on H with coefficient . Then, for
. Then, for ,
,

That is, A - γ f is strongly monotone with coefficient .
.
Lemma 2.8. [5]Assume A to be a strongly positive linear-bounded operator on H with coefficient and 0 < ρ ≤ ||A||-1. Then,
and 0 < ρ ≤ ||A||-1. Then,  .
.
For solving the generalized mixed equilibrium problem and the mixed equilibrium problem, let us give the following assumptions for the bifunction F, the function φ and the set C:
(H1) F(x, x) = 0, ∀x ∈ C;
(H2) F is monotone, that is, F(x, y) + F(y, x) ≤ 0 ∀x, y ∈ C;
(H3) for each y ∈ C, x α F(x, y) is weakly upper semicontinuous;
(H4) for each x ∈ C, y α F(x, y) is convex;
(H5) for each x ∈ C, y α F(x, y) is lower semicontinuous;
(B1) for each x ∈ H and λ > 0, there exist abounded subset G x ⊆ C and y x ∈ C such that for any z ∈ C \n G x ,

(B2) C is a bounded set.
Lemma 2.9. [15]Let C be a nonempty closed convex subset of H. Let F : C ×C → ℝ be a bifunction satisfies (H1)-(H5), and let φ : C → ℝ∪{+∞} be a proper lower semi continuous and convex function. Assume that either (B1) or (B2) holds. For λ > 0 and x ∈ H, define a mapping as follows:
as follows:

Then, the following properties hold:
-
(i)
For each x ∈ H,
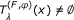 ;
; -
(ii)
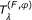 is single-valued;
is single-valued;
-
(iii)
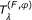 is firmly nonexpansive, that is, for any x, y ∈ H,
is firmly nonexpansive, that is, for any x, y ∈ H, 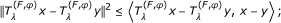
-
(iv)
 ;
; -
(v)
MEP(F, φ) is closed and convex.
Lemma 2.10. [16]Assume {a n } to be a sequence of nonnegative real numbers such that

where {b n } is a sequence in (0, 1) and {c n } is a sequence in ℝ such that
-
(1)
 ,
, -
(2)
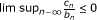 or
or

Then, limn →∞a n = 0.
3. Main results
In this section, we are in a position to state and prove our main results.
Theorem 3.1. Let C be a nonempty closed convex subset of a real Hilbert space H. Let F be bifunction from C × C to ℝ satisfying (H1)-(H5), and let φ : C → ℝ ∪ {+∞} be a proper lower semicontinuous and convex function with either (B1) or (B2). Let B, D be two ξ, β-inverse strongly monotone mapping of C into H, respectively, and let S : C → C be a nonexpansive mapping. Let f : C → C be a contraction mapping with η ∈ (0, 1), and let A be a strongly positive linear-bounded operator with and
and . Assume that Θ := F (S) ∩ VI(C, B) ∩ GMEP(F, φ, D) ≠ ∅. Let {x
n
}, {y
n
} and {u
n
} be sequences generated by the following iterative algorithm:
. Assume that Θ := F (S) ∩ VI(C, B) ∩ GMEP(F, φ, D) ≠ ∅. Let {x
n
}, {y
n
} and {u
n
} be sequences generated by the following iterative algorithm:

where {δn} and {β n } are two sequences in (0, 1) satisfying the following conditions:
(C1) limn →∞β
n
= 0 and ,
,
(C2) {δ n } ⊂ [0, b], for some b ∈ (0, 1) and limn →∞|δn+1- δ n | = 0,
(C3) {λ n } ⊂ [c, d] ⊂ (0, 2β) and limn →∞|λn+1- λ n | = 0,
(C4) {α n } ⊂ [e, g] ⊂ (0, 2ξ) and limn →∞|αn+1- α n | = 0.
Then, {x n } converges strongly to z ∈ Θ, which is the unique solution of the variational inequality

Proof. We may assume, in view of β
n
→ 0 as n → ∞, that β
n
∈ (0, ||A||-1). By Lemma 2.8, we obtain  , ∀
n
∈ ℕ.
, ∀
n
∈ ℕ.
We divide the proof of Theorem 3.1 into six steps.
Step 1. We claim that the sequence {x n } is bounded.
Now, let p ∈ Θ. Then, it is clear that

Let  , D be β-inverse strongly monotone and 0 ≤ λ
n
≤ 2β. Then, we have
, D be β-inverse strongly monotone and 0 ≤ λ
n
≤ 2β. Then, we have

Let z n = PC(Su n - α n BSu n ) and S - α n BS be a nonexpansive mapping. Then, we have from Lemma 2.4 that

and

Similarly, and let w n = P C (Sy n - α n BSy n ) in (3.4). Then, we can prove that

which yields that

This shows that {x n } is bounded. Hence, {u n }, {z n }, {y n }, {w n }, {BSu n }, {BSy n }, {Az n } and {f(x n )} are also bounded.
We can choose some appropriate constant M > 0 such that

Step 2. We claim that limn→∞||xn+1- x n || = 0.
It follows from Lemma 2.9 that  and
and  for all n ≥ 1, and we get
for all n ≥ 1, and we get

and

Take y = un-1in (3.8) and y = u n in (3.7), and then we have

and

Adding the above two inequalities, the monotonicity of F implies that

and

Without loss of generality, let us assume that there exists c ∈ ℝ such that λ n > c > 0, ∀n ≥ 1. Then, we have

and hence,

Since S - α n BS is nonexpansive for each n ≥ 1, we have

Substituting (3.9) into (3.10), we obtain

From (3.1), we have

Substituting (3.11) into (3.12) yields

Since w n = P C (Sy n - α n BSy n ) and S - α n BS is nonexpansive mapping, we have

Also, from (3.1) and (3.13), we have

Set  and
and

Then, we have

From the conditions (C1)-(C4), we find that

Therefore, applying Lemma 2.10 to (3.16), we have

Step 3. We claim that limn→∞||Sw n - w n || = 0.
For any p ∈ Θ and Lemma 2.4, we obtain

From (3.1) and (3.18), we have

From (3.1), (3.5), (3.19) and Lemma 2.1(iv), we have

It follows that

From condition (C1) and (3.17), we obtain

From w n = PC(Sy n - α n BSy n ), (3.19) and Lemma 2.4, we have

Using (3.1), (3.19) and (3.23), we obtain

It follows that

From condition (C1), (3.17) and (3.22), we obtain

Since P C is firmly nonexpansive, we have

Hence, we have

Using (3.24) and (3.28), we have

It follows that

From the condition (C1), (3.17), (3.22) and (3.26), we obtain

Note that

From (3.1) and (3.32), we can compute

It follows that

which implies that

In addition, from the firmly nonexpansivity of  , we have
, we have

Hence, we obtain

Substituting (3.36) into (3.32) to get

and hence,

It follows that

This together with ||xn+1- x n || → 0, ||Dx n - D p || → 0, β n → 0 as n → ∞ and the condition on λ n implies that

Consequently, from (3.17) and (3.40)

From (3.1) and condition (C1), we have

Since S - α n BS is nonexpansive mapping(Lemma 2.4), we have

Next, we will show that ||x n - y n || → 0 as n → ∞.
We consider xn+1- y n = δ n (w n - y n ) = δn(w n - z n + z n - y n ).
From (3.43), we have

From the condition (C2), (3.41) and (3.42), it follows that

From (3.17) and (3.45), we obtain

We observe that

Consequently, we obtain

Step 4. We prove that the mapping PΘ(γf + (I - A)) has a unique fixed point.
Let f be a contraction of C into itself with coefficient η ∈ (0, 1). Then, we have

Since  , it follows that PΘ(γf + (I - A)) is a contraction of C into itself. Therefore, by the Banach Contraction Mapping Principle, it has a unique fixed point, say z ∈ C, that is,
, it follows that PΘ(γf + (I - A)) is a contraction of C into itself. Therefore, by the Banach Contraction Mapping Principle, it has a unique fixed point, say z ∈ C, that is,

Step 5. We claim that q ∈ F(S) ∩ VI(C, B) ∩ GMEP(F, φ, D).
First, we show that q ∈ F(S).
Assume q ∉ F(S). Since  and q ≠ Sq, based on Opial's condition (Lemma 2.6), it follows that
and q ≠ Sq, based on Opial's condition (Lemma 2.6), it follows that

This is a contradiction. Thus, we have q ∈ F(S).
Next, we prove that q ∈ GMEP(F, φ, D).
From Lemma 2.9 that  for all n ≥ 1 is equivalent to
for all n ≥ 1 is equivalent to

From (H2), we also have

Replacing n by n i , we obtain

Let y t = t y + (1 - t)q for all t ∈ (0, 1] and y ∈ C. Since y ∈ C and q ∈ C, we obtain y t ∈ C. Hence, from (3.49), we have

Since  , i → ∞ we obtain
, i → ∞ we obtain  . Furthermore, by the monotonicity of D, we have
. Furthermore, by the monotonicity of D, we have

Hence, from (H4), (H5) and the weak lower semicontinuity of φ,  and
and  , we have
, we have

From (H1), (H4) and (3.51), we also get

Dividing by t, we get

Letting t → 0 in the above inequality, we arrive that, for each y ∈ C,

This implies that q ∈ GMEP(F, φ, D).
Finally, we prove that q ∈ VI(C, B).
We define the maximal monotone operator:

Since B is ξ-inverse strongly monotone and by condition (C4), we have

Then, Q is maximal monotone. Let (q1, q2) ∈ G(Q). Since q2 - Bq1 ∈ N C q1 and w n ∈ C, we have 〈q1 - w n , q2- Bq1〉 ≥ 0. On the other hand, from w n = P C (Sy n - α n BSy n ), we have

that is,

Therefore, we obtain

Noting that  as i → ∞, we obtain
as i → ∞, we obtain

Since Q is maximal monotone, we obtain that q ∈ Q-10, and hence q ∈ VI(C, B). This implies q ∈ Θ. Since z = PΘ(γf + (I - A))(z), we have

On the other hand, we have

From (3.46) and (3.53), we obtain that

Step 6. Finally, we claim that x n → z, where z = PΘ(γf + (I - A))(z).
We note that

which implies that

On the other hand, we have

where K is an appropriate constant such that K ≥ supn≥1{||x n - z||2}.
Set  and
and  . Then, we have
. Then, we have

From the condition (C1) and (3.54), we see that

Therefore, applying Lemma 2.10 to (3.58), we get that {x n } converges strongly to z ∈ Θ.
This completes the proof. □
Corollary 3.2. Let C be a nonempty closed convex subset of a real Hilbert space H, let B be ξ-inverse-strongly monotone mapping of C into H, and let S : C → C be a nonexpansive mapping. Let f : C → C be a contraction mapping with η ∈ (0, 1), and let A be a strongly positive linear-bounded operator with and
and . Assume that Θ := F(S) ∩ VI(C, B) ≠ ∅. Let {x
n
} and {y
n
} be sequence generated by the following iterative algorithm:
. Assume that Θ := F(S) ∩ VI(C, B) ≠ ∅. Let {x
n
} and {y
n
} be sequence generated by the following iterative algorithm:

where {δ n } and {β n } are two sequences in (0, 1) satisfying the following conditions:
(C1) limn → ∞β
n
= 0 and ,
,
(C2) {δ n } ⊂ [0, b], for some b ∈ (0, 1) and limn → ∞|δn+1- δ n | = 0,
(C3) {α n } ⊂ [e, g] ⊂ (0, 2ξ) and limn → ∞|αn+1- α n | = 0.
Then, {x n } converges strongly to z ∈ Θ, which is the unique solution of the variational inequality

Proof. Put F(x, y) = φ = D = 0 for all x, y ∈ C and λ n = 1 for all n ≥ 1 in Theorem 3.1, we get u n = x n . Hence, {x n } converges strongly to z ∈ Θ, which is the unique solution of the variational inequality (3.59). □
Corollary 3.3. [12]Let C be a nonempty closed convex subset of a real Hilbert space H and let F be bifunction from C × C to ℝ satisfying (H1)-(H5). Let S : C → C be a nonexpansive mapping and let f : C → C be a contraction mapping with η ∈ (0, 1). Assume that Θ := F(S) ∩ EP(F) ≠ ∅. Let {x n }, {y n } and {u n } be sequence generated by the following iterative algorithm:

where {δ n } and {β n } are two sequences in (0, 1) and {λ n } ⊂ (0, ∞) satisfying the following conditions:
(C1) limn → ∞β
n
= 0 and ,
,
(C2) {δ n } ⊂ [0, b], for some b ∈ (0, 1) and limn → ∞|δn+1- δ n | = 0,
(C3) limn → ∞|λn+1- λ n | = 0.
Then, {x n } converges strongly to z ∈ Θ.
Proof. Put φ = D = 0, γ = 1, A = I and α n = 0 in Theorem 3.1. Then, we have P C (Su n ) = Su n and P C (Sy n ) = Sy n . Hence, {x n } generated by (3.60) converges strongly to z ∈ Θ. □
References
Goebeland K, Kirk WA: Topics in Metric Fixed Point Theory. Cambridge University Press, Cambridge; 1990.
Takahashi W: Nonlinear Functional Analysis. Yokohama Publishers, Yokohama; 2000.
Peng JW, Yao JC: A new hybrid-extragradient method for generalized mixed equilibrium problems and fixed point problems and variational inequality problems. Taiwanese J Math 2008, 12: 1401–1433.
Peng JW, Yao JC: Two extragradient method for generalized mixed equilibrium problems, nonexpansive mappings and monotone mappings. Comput Math Appl 2009, 58: 1287–1301. 10.1016/j.camwa.2009.07.040
Marino G, Xu HK: A general iterative method for nonexpansive mapping in Hilbert spaces. J Math Anal Appl 2006, 318: 43–52. 10.1016/j.jmaa.2005.05.028
Takahashi W, Toyoda M: Weak convergence theorems for nonexpansive mappings and monotone mappings. J Optim Theory Appl 2003, 118: 417–428. 10.1023/A:1025407607560
Yamada I: The hybrid steepest descent method for the variational inequality problem of the intersection of fixed point sets of nonexpansive mappings. In Inherently Parallel Algorithm for Feasibility and Optimization. Edited by: Butnariu D, Censor Y, Reich S. Elsevier, Amsterdam; 2001:473–504.
Su Y, Shang M, Qin X: An iterative method of solution for equilibrium and optimization problems. Nonlinear Anal Ser A Theory Methods Appl 2008, 69: 2709–2719. 10.1016/j.na.2007.08.045
Takahashi S, Takahashi W: Strong convergence theorems for a generalized equilibrium problem and a nonexpansive mappings in a Hilbert space. Nonlinear Anal Ser A Theory Methods Appl 2008, 69: 1025–1033. 10.1016/j.na.2008.02.042
Chantarangsi W, Jaiboon C, Kumam P: A viscosity hybrid steepest descent method for generalized mixed equilibrium problems and variational inequalities, for relaxed cocoercive mapping in Hilbert spaces. Abstr Appl Anal 2010, 2010: 39. Article ID 390972
Jaiboon C: The hybrid steepest descent method for addressing fixed point problems and system of equilibrium problems. Thai J Math 2010,8(2):275–292.
Jung JS: Strong convergence of composite iterative methods for equilibrium problems and fixed point problems. Appl Math Comput 2009, 213: 498–505. 10.1016/j.amc.2009.03.048
Rockafellar RT: On the maximality of sums of nonlinear monotone operators. Trans Am Math Soc 1970, 149: 75–88. 10.1090/S0002-9947-1970-0282272-5
Opial Z: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull Am Math Soc 1967, 73: 595–597.
Ceng LC, Yao JC: A hybrid iterative scheme for mixed equilibrium problems and fixed point problems. J Comput Appl Math 2008, 214: 186–201. 10.1016/j.cam.2007.02.022
Xu HK: Viscosity approximation methods for nonexpansive mappings. J Math Anal Appl 2004, 298: 279–291. 10.1016/j.jmaa.2004.04.059
6. Acknowledgements
This research was partially supported by the Research Fund, Rajamangala University of Technology Rattanakosin. The first author was supported by the 'Centre of Excellence in Mathematics', the Commission on High Education, Thailand for Ph.D. program at King Mongkuts University of Technology Thonburi (KMUTT). The second author was supported by Rajamangala University of Technology Rattanakosin Research and Development Institute, the Thailand Research Fund and the Commission on Higher Education under Grant No. MRG5480206. The third author was supported by the NRU-CSEC Project No. 54000267. Helpful comments by anonymous referees are also acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
4. Competing interests
The authors declare that they have no competing interests.
5. Authors' contributions
All authors contribute equally and significantly in this research work. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Onjai-uea, N., Jaiboon, C. & Kumam, P. A relaxed hybrid steepest descent method for common solutions of generalized mixed equilibrium problems and fixed point problems. Fixed Point Theory Appl 2011, 32 (2011). https://doi.org/10.1186/1687-1812-2011-32
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-32
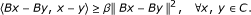
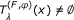 ;
;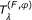 is single-valued;
is single-valued;
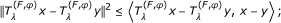
 ;
; ,
,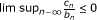 or
or
