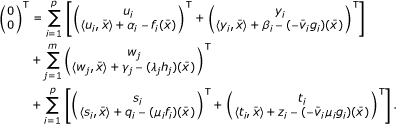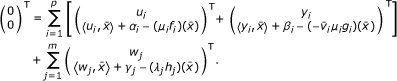- Research
- Open access
- Published:
On ε-optimality conditions for multiobjective fractional optimization problems
Fixed Point Theory and Applications volume 2011, Article number: 6 (2011)
Abstract
A multiobjective fractional optimization problem (MFP), which consists of more than two fractional objective functions with convex numerator functions and convex denominator functions, finitely many convex constraint functions, and a geometric constraint set, is considered. Using parametric approach, we transform the problem (MFP) into the non-fractional multiobjective convex optimization problem (NMCP)
v
with parametric v ∈ ℝ p , and then give the equivalent relation between (weakly) ε-efficient solution of (MFP) and (weakly)  -efficient solution of
-efficient solution of 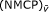 . Using the equivalent relations, we obtain ε- optimality conditions for (weakly) ε- efficient solution for (MFP). Furthermore, we present examples illustrating the main results of this study.
. Using the equivalent relations, we obtain ε- optimality conditions for (weakly) ε- efficient solution for (MFP). Furthermore, we present examples illustrating the main results of this study.
2000 Mathematics Subject Classification: 90C30, 90C46.
1 Introduction
We need constraint qualifications (for example, the Slater condition) on convex optimization problems to obtain optimality conditions or ε- optimality conditions for the problem.
To get optimality conditions for an efficient solution of a multiobjective optimization problem, we often formulate a corresponding scalar problem. However, it is so difficult that such scalar program satisfies a constraint qualification which we need to derive an optimality condition. Thus, it is very important to investigate an optimality condition for an efficient solution of a multiobjective optimization problem which holds without any constraint qualification.
Jeyakumar et al. [1, 2], Kim et al. [3], and Lee et al. [4], gave optimality conditions for convex (scalar) optimization problems, which hold without any constraint qualification. Very recently, Kim et al. [5] obtained ε- optimality theorems for a convex multiobjective optimization problem. The purpose of this article is to extend the ε- optimality theorems of Kim et al. [5] to a multiobjective fractional optimization problem (MFP).
Recently, many authors [5–15] have paid their attention to investigate properties of (weakly) ε- efficient solutions, ε- optimality conditions, and ε- duality theorems for multiobjective optimization problems, which consist of more than two objective functions and a constrained set.
In this article, an MFP, which consists of more than fractional objective functions with convex numerator functions, and convex denominator functions and finitely many convex constraint functions and a geometric constraint set, is considered. We discuss ε- efficient solutions and weakly ε- efficient solutions for (MFP) and obtain ε- optimality theorems for such solutions of (MFP) under weakened constraint qualifications. Furthermore, we prove ε- optimality theorems for the solutions of (MFP) which hold without any constraint qualifications and are expressed by sequences, and present examples illustrating the main results obtained.
2 Preliminaries
Now, we give some definitions and preliminary results. The definitions can be found in [16–18]. Let g : ℝ n → ℝ ∪ {+∞} be a convex function. The subdifferential of g at a is given by

where domg: = {x ∈ ℝ n | g(x) < ∞} and ⟨·, ·⟩ is the scalar product on ℝ n . Let ε ≧ 0. The ε- subdifferential of g at a ∈ domg is defined by

The conjugate function of g : ℝ n → ℝ ∪ {+∞} is defined by

The epigraph of g, epig, is defined by

For a nonempty closed convex set C ⊂ ℝ n , δ
C
: ℝ n → ℝ ∪ {+∞} is called the indicator of C if  .
.
Lemma 2.1[19]If h : ℝ n → ℝ ∪ {+∞} is a proper lower semicontinuous convex function and if a ∈ domh, then

Lemma 2.2[20]Let h : ℝ n → ℝ be a continuous convex function and u : ℝ n → ℝ ∪ {+∞} be a proper lower semicontinuous convex function. Then

Now, we give the following Farkas lemma which was proved in [2, 5], but for the completeness, we prove it as follows:
Lemma 2.3 Let h i : ℝ n → ℝ, i = 0, 1, ⋯, l be convex functions. Suppose that {x ∈ ℝ n | h i (x) ≦ 0, i = 1, ⋯, l} ≠ ∅. Then the following statements are equivalent:
(i) {x ∈ ℝ n | h i (x) ≦ 0, i = 1, ..., l} ⊆ {x ∈ ℝ n | h0(x) ≧ 0}
(ii) .
.
Proof. Let Q = {x ∈ ℝ n | h
i
(x) ≦ 0, i = 1, ..., l}. Then Q ≠ ∅ and by Lemma 2.1 in [2],  . Hence, by Lemma 2.2, we can verify that (i) if and only if (ii).
. Hence, by Lemma 2.2, we can verify that (i) if and only if (ii).
Lemma 2.4[16]Let h
i
: ℝ n → ℝ ∪ {+∞}, i =, 1, ⋯, m be proper lower semi-continuous convex functions. Let ε ≧ 0. if , where ri domh
i
is the relative interior of domh
i
, then for all
, where ri domh
i
is the relative interior of domh
i
, then for all ,
,

3 ε-optimality theorems
Consider the following MFP:

Let f i : ℝ n → ℝ, i = 1, ..., p be convex functions, g i : ℝ n → ℝ, i = 1, ..., p, concave functions such that for any x ∈ Q, f i (x) ≧ 0 and g i (x) > 0, i = 1, ..., p, and h j : ℝ n → ℝ, j = 1, ..., m, convex functions. Let ε = (ε1, ..., ε p ), where ε i ≧ 0, i = 1, ..., p.
Now, we give the definition of ε- efficient solution of (MFP) which can be found in [11].
Definition 3.1 The point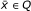 is said to be an ε-efficient solution of (MFP) if there does not exist x ∈ Q such that
is said to be an ε-efficient solution of (MFP) if there does not exist x ∈ Q such that

When ε = 0, then the ε- efficiency becomes the efficiency for (MFP) (see the definition of efficient solution of a multiobjective optimization problem in [21]).
Now, we give the definition of weakly ε- efficient solution of (MFP) which is weaker than ε- efficient solution of (MFP).
Definition 3.2 A point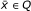 is said to be a weakly ε-efficient solution of (MFP) if there does not exist x ∈ Q such that
is said to be a weakly ε-efficient solution of (MFP) if there does not exist x ∈ Q such that

When ε = 0, then the weak ε- efficiency becomes the weak efficiency for (MFP) (see the definition of efficient solution of a multiobjective optimization problem in [21]).
Using parametric approach, we transform the problem (MFP) into the nonfractional multiobjective convex optimization problem (NMCP) v with parametric v ∈ ℝ p :

Adapting Lemma 4.1 in [22] and modifying Proposition 3.1 in [12], we can obtain the following proposition:
Proposition 3.1 Let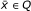 . Then the following are equivalent:
. Then the following are equivalent:
(i) is an ε-efficient solution of (MFP).
is an ε-efficient solution of (MFP).
(ii) is an
is an -efficient solution of
-efficient solution of  , where
, where 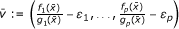 and
and  .
.
(iii) 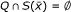 or
or

where .
.
Proof. (i) ⇔ (ii): It follows from Lemma 4.1 in [22].
-
(ii)
⇒ (iii): Let
 be an
be an  -efficient solution of
-efficient solution of 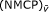 , where
, where 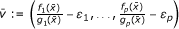 and
and  . Then
. Then 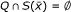 or
or 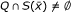 . Suppose that
. Suppose that 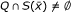 . Then for any
. Then for any 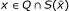 and all i = 1, . . . p,
and all i = 1, . . . p, 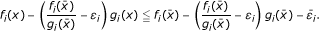
Hence the  -efficiency of
-efficiency of  yields
yields

for any 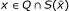 and all i = 1, ..., p. Thus we have, for all
and all i = 1, ..., p. Thus we have, for all 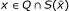 ,
,

-
(iii)
⇒ (ii): Suppose that
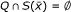 . Then there does not exist x ∈ Q such that
. Then there does not exist x ∈ Q such that 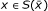 ; that is, there does not exist x ∈ Q such that
; that is, there does not exist x ∈ Q such that 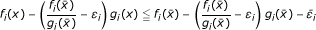
for all i = 1, ..., p. Hence, there does not exist x ∈ Q such that

Therefore,  is an
is an  -efficient solution of
-efficient solution of 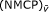 , where
, where 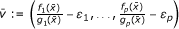 .
.
Assume that 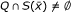 . Then, from this assumption
. Then, from this assumption

for any 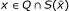 . Suppose to the contrary that
. Suppose to the contrary that  is not an
is not an  -efficient solution of
-efficient solution of 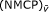 . Then, there exist
. Then, there exist  and an index j such that
and an index j such that

Therefore,  and
and  , which contradicts the above inequality. Hence,
, which contradicts the above inequality. Hence,  is an
is an  -efficient solution of
-efficient solution of 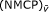 .
.
We can easily obtain the following proposition:
Proposition 3.2 Let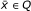 and suppose that
and suppose that . Then the following are equivalent:
. Then the following are equivalent:
(i) is a weakly ε-efficient solution of (MFP).
is a weakly ε-efficient solution of (MFP).
(ii) is a weakly
is a weakly -efficient solution of
-efficient solution of , where
, where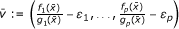 and
and .
.
(iii) there exists
 such that
such that

Proof. (i) ⇔ (ii): The proof is also following the similar lines of Proposition 3.1.
-
(ii)
⇒ (iii): Let φ(x) = (φ 1(x), ..., φ p (x)), ∀x ∈ Q, where
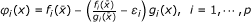 . Then, φ
i
(x), i = 1,⋯, p, are convex. Since
. Then, φ
i
(x), i = 1,⋯, p, are convex. Since 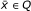 is a weakly ε- efficient solution of
is a weakly ε- efficient solution of 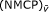 , where
, where 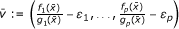 ,
, 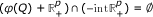 , and hence, it follows from separation theorem that there exist
, and hence, it follows from separation theorem that there exist 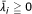 , i = 1, ..., p,
, i = 1, ..., p,  such that
such that 
Thus (iii) holds.
-
(iii)
⇒ (ii): If (ii) does not hold, that is,
 is not a weakly
is not a weakly  -efficient solution of
-efficient solution of 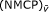 , then (iii) does not hold. □
, then (iii) does not hold. □
We present a necessary and sufficient ε-optimality theorem for ε-efficient solution of (MFP) under a constraint qualification, which will be called the closedness assumption.
Theorem 3.1 Let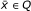 and assume that
and assume that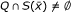 and
and i = 1, ..., p. Suppose that
i = 1, ..., p. Suppose that

is closed, where , i = 1, ..., p. Then the following are equivalent.
, i = 1, ..., p. Then the following are equivalent.
(i) is an ε-efficient solution of (MFP).
is an ε-efficient solution of (MFP).
(ii)

(iii) there exist α
i
≧ 0,  , β
i
≧ 0,
, β
i
≧ 0,  , i = 1, ..., p, λ
j
≧ 0, γ
j
≧ 0,
, i = 1, ..., p, λ
j
≧ 0, γ
j
≧ 0,  , j = 1, ..., m, μ
i
≧ 0, q
i
≧ 0,
, j = 1, ..., m, μ
i
≧ 0, q
i
≧ 0,  , z
i
≧ 0,
, z
i
≧ 0, 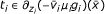 i = 1, ..., p such that
i = 1, ..., p such that

and

Proof. Let  .
.
-
(i)
⇔ (by Proposition 3.1) h 0(x) ≧ 0,
 .
.
⇔  , i = 1, ..., p, h
j
(x) ≦ 0, j = 1, ..., m} ⊂ {x | h0(x) ≧ 0}.
, i = 1, ..., p, h
j
(x) ≦ 0, j = 1, ..., m} ⊂ {x | h0(x) ≧ 0}.
⇔ (by lemma 2.3)

Thus by the closedness assumption, (i) is equivalent to (ii).
-
(ii)
⇔ (iii): (ii) ⇔ (by Lemma 2.1), there exist α i ≧ 0,
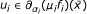 , i = 1, ..., p, β
i
≧ 0,
, i = 1, ..., p, β
i
≧ 0,  , i = 1, ..., p, λ
j
≧ 0, γ
j
≧ 0,
, i = 1, ..., p, λ
j
≧ 0, γ
j
≧ 0, 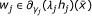 , j = 1, ..., m, μ
i
≧ 0, q
i
≧ 0,
, j = 1, ..., m, μ
i
≧ 0, q
i
≧ 0,  , i = 1, ..., p, z
i
≧ 0,
, i = 1, ..., p, z
i
≧ 0, 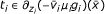 , i = 1, ..., p such that
, i = 1, ..., p such that 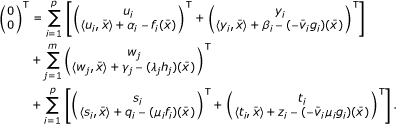
⇔ there exist α
i
≧ 0, 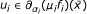 , β
i
≧ 0,
, β
i
≧ 0,  , i = 1, ..., p, λ
j
≧ 0, γ
j
≧ 0,
, i = 1, ..., p, λ
j
≧ 0, γ
j
≧ 0, 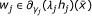 , j = 1, ..., m, μ
i
≧ 0, q
i
≧ 0,
, j = 1, ..., m, μ
i
≧ 0, q
i
≧ 0,  , z
i
≧ 0,
, z
i
≧ 0, 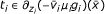 i = 1, ..., p such that
i = 1, ..., p such that

and

⇔ (iii) holds. □
Now we give a necessary and sufficient ε-optimality theorem for ε-efficient solution of (MFP) which holds without any constraint qualification.
Theorem 3.2 Let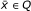 . Suppose that
. Suppose that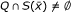 and
and , i = 1, ..., p. Then
, i = 1, ..., p. Then is an ε-efficient solution of (MFP) if and only if there exist α
i
≧ 0,
is an ε-efficient solution of (MFP) if and only if there exist α
i
≧ 0, 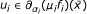 , i = 1, ..., p, β
i
≧ 0,
, i = 1, ..., p, β
i
≧ 0,  , i = 1, ..., p,
, i = 1, ..., p,  ,
,  ,
,  , j = 1, ..., m,
, j = 1, ..., m,  ,
,  ,
,  ,
,  ,
,  , k = 1, ..., p such that
, k = 1, ..., p such that

and

Proof.  is an ε-efficient solution of (MFP)
is an ε-efficient solution of (MFP)
⇔ (from the proof of Theorem 3.1)

⇔ (by Lemma 2.1) there exist α
i
≧ 0, 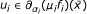 , i = 1, ..., p, β
i
≧ 0,
, i = 1, ..., p, β
i
≧ 0,  , i = 1, ..., p,
, i = 1, ..., p,  ,
,  ,
,  , j = 1, ..., m,
, j = 1, ..., m,  ,
,  ,
,  ,
,  ,
,  , k = 1, ..., p, such that
, k = 1, ..., p, such that

⇔ there exist α
i
≧ 0, 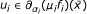 , i = 1, ..., p, β
i
≧ 0,
, i = 1, ..., p, β
i
≧ 0,  , i = 1, ..., p,
, i = 1, ..., p,  ,
,  ,
,  , j = 1, ..., m,
, j = 1, ..., m,  ,
,  ,
,  ,
,  ,
,  , k = 1, ..., p, such that
, k = 1, ..., p, such that

and

We present a necessary and sufficient ε-optimality theorem for weakly ε-efficient solution of (MFP) under a constraint qualification.
Theorem 3.3 Let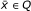 and assume that
and assume that , i = 1, ..., p, and
, i = 1, ..., p, and is closed. Then the following are equivalent.
is closed. Then the following are equivalent.
(i) is a weakly ε-efficient solution of (MFP).
is a weakly ε-efficient solution of (MFP).
(ii) there exist μ
i
≧ 0, i = 1, ..., p, 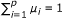 such that
such that

where , i = 1, ..., p.
, i = 1, ..., p.
(iii) there exist μ
i
≧ 0, 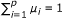 , α
i
≧ 0,
, α
i
≧ 0, 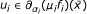 , β
i
≧ 0,
, β
i
≧ 0,  , i = 1, ..., p, λ
j
≧ 0, γ
j
≧ 0,
, i = 1, ..., p, λ
j
≧ 0, γ
j
≧ 0, 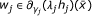 , j = 1, ..., m, such that
, j = 1, ..., m, such that

and

Proof. (i) ⇔ (ii):  is a weakly ε-efficient solution of (MFP)
is a weakly ε-efficient solution of (MFP)
⇔ (by Proposition 3.2) there exist μ
i
≧ 0, i = 1, ..., p, 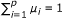 such that
such that

⇔ there exist μ
i
≧ 0, i = 1, ..., p, 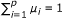 such that
such that

⇔ (by Lemma 2.3) there exist μ
i
≧ 0, i = 1, ..., p, 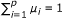 such that
such that

Thus, by the closedness assumption, (i) is equivalent to (ii).
-
(ii)
⇔ (iii): (ii) ⇔ (by Lemma 2.1) there exist μ i ≧ 0,
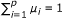 , α
i
≧ 0,
, α
i
≧ 0, 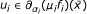 , β
i
≧ 0,
, β
i
≧ 0,  , i = 1, ..., p, λ
j
≧ 0, γ
j
≧ 0,
, i = 1, ..., p, λ
j
≧ 0, γ
j
≧ 0, 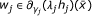 , j = 1, ..., m, such that
, j = 1, ..., m, such that 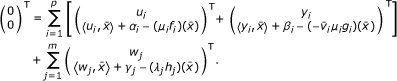
⇔ (iii) holds. □
Now, we propose a necessary and sufficient ε-optimality theorem for weakly ε-efficient solution of (MFP) which holds without any constraint qualification.
Theorem 3.4 Let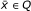 and assume that
and assume that . Then
. Then is a weakly ε-efficient solution of (MFP) if and only if there exist μ
i
≧ 0, i = 1, ..., p,
is a weakly ε-efficient solution of (MFP) if and only if there exist μ
i
≧ 0, i = 1, ..., p, 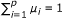 , α
i
≧ 0,
, α
i
≧ 0, 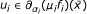 , i = 1, ..., p, β
i
≧ 0,
, i = 1, ..., p, β
i
≧ 0,  , i = 1, ..., p,
, i = 1, ..., p,  ,
,  ,
,  , j = 1, ..., m, such that
, j = 1, ..., m, such that

and

Proof.  is a weakly ε-efficient solution of (MFP)
is a weakly ε-efficient solution of (MFP)
⇔ ((from the proof of Theorem 3.3) there exist μ
i
≧ 0, i = 1, ..., p, 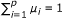 such that
such that

⇔ (by Lemma 2.1) there exist μ
i
≧ 0, i = 1, ..., p, 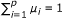 , α
i
≧ 0,
, α
i
≧ 0, 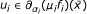 , i = 1, ..., p, β
i
≧ 0,
, i = 1, ..., p, β
i
≧ 0,  , i = 1, ..., p,
, i = 1, ..., p,  ,
,  ,
,  , j = 1, ..., m, such that
, j = 1, ..., m, such that

⇔ there exist μ
i
≧ 0, i = 1, ..., p, 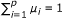 , α
i
≧ 0,
, α
i
≧ 0, 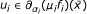 , i = 1, ..., p, β
i
≧ 0,
, i = 1, ..., p, β
i
≧ 0,  , i = 1, ..., p,
, i = 1, ..., p,  ,
,  ,
,  , j = 1, ..., m, such that
, j = 1, ..., m, such that

and

□
Now, we give examples illustrating Theorems 3.1, 3.2, 3.3, and 3.4.
Example 3.1 Consider the following MFP:

Let , and f1(x1, x2) = x1, g1(x1, x2) = 1, f2(x1, x2) = x2, g2(x1, x2) = x1, h1(x1, x2) = -x1+ 1 and h2(x1, x2) = -x2 + 1.
, and f1(x1, x2) = x1, g1(x1, x2) = 1, f2(x1, x2) = x2, g2(x1, x2) = x1, h1(x1, x2) = -x1+ 1 and h2(x1, x2) = -x2 + 1.
(1)Let . Then
. Then is an ε-efficient solution of (MFP)1.
is an ε-efficient solution of (MFP)1.
Let and
and . Then
. Then , and
, and

Thus, . It is clear that
. It is clear that and
and . Let
. Let . Then
. Then

where coD is the convexhull of a set D and cone coD is the cone generated by coD. Thus A is closed. Let . Then
. Then
B = {(1, 0)} × [0, ∞)+{(0, 0)} × [1, ∞)+{(0, 1)} × [0, ∞)+{(-1, 0)} × [0, ∞)+A. Since (0,-1,-1) ∈ A, (0, 0, 0) ∈ B. Thus (ii) of Theorem 3.1 holds. Let α1 = β1 = γ1 = q1 = z1 = α2 = β2 = γ2 = q2 = z2 = 0, and let μ1 = μ2 = 1, and λ1 = 0 and λ1 = 2. Moreover,  ,
,  ,
,  ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
,  .
.
Thus, and
and .
.
Thus, (iii) of Theorem 3.1 holds.
(2) Let . Then
. Then is not an ε-efficient solution of (MFP)1, but
is not an ε-efficient solution of (MFP)1, but is a weakly ε-efficient solution of (MFP)1.
is a weakly ε-efficient solution of (MFP)1.
Let . Then
. Then

Hence, C is closed. Moreover, , and
, and . Let
. Let and
and . Then,
. Then, ,
,  . Let μ1 = 1 and μ2 = 1. Then,
. Let μ1 = 1 and μ2 = 1. Then,

Since (-1, 0,-1) ∈ C,  . So, (ii) of Theorem 3.3 holds. Let α1 = β1 = γ1 = α2 = β2 = γ2 = 0, λ1 = 1 and λ2 = 0. Then,
. So, (ii) of Theorem 3.3 holds. Let α1 = β1 = γ1 = α2 = β2 = γ2 = 0, λ1 = 1 and λ2 = 0. Then,

and

Thus, (iii) of Theorem 3.3 holds.
Example 3.2 Consider the following MFP:

Let , and f1(x1, x2) = -x1 + 1, g1(x1, x2) = 1, f2(x1, x2) = x2, g2(x1, x2) = -x1 + 1, h1(x1, x2) = [max{0, x1}]2and h2(x1, x2) = -x2 + 1.
, and f1(x1, x2) = -x1 + 1, g1(x1, x2) = 1, f2(x1, x2) = x2, g2(x1, x2) = -x1 + 1, h1(x1, x2) = [max{0, x1}]2and h2(x1, x2) = -x2 + 1.
(1) Let . Then,
. Then, is an ε-efficient solution of (MFP)2. Let
is an ε-efficient solution of (MFP)2. Let . Then, clA = cone co{(0, -1, -1), (1, 0, 0), (-1, 0, 0), (1, 1, 1), (0, 0, 1)}. Here, (1, 0, 0) ∈ clA, but (1, 0, 0) ∈ A, where clA is the closure of the set A. Thus, A is not closed. Let Q = {(x1, x2) ∈ ℝ n | h1(x1, x2) ≦ 0, h2(x1, x2) ≦ 0}. Then,
. Then, clA = cone co{(0, -1, -1), (1, 0, 0), (-1, 0, 0), (1, 1, 1), (0, 0, 1)}. Here, (1, 0, 0) ∈ clA, but (1, 0, 0) ∈ A, where clA is the closure of the set A. Thus, A is not closed. Let Q = {(x1, x2) ∈ ℝ n | h1(x1, x2) ≦ 0, h2(x1, x2) ≦ 0}. Then,  . Let
. Let , i = 1, 2. Then,
, i = 1, 2. Then,  . Let α1 = β1 = α2 = β2 = 0,
. Let α1 = β1 = α2 = β2 = 0,  ,
,  ,
,  ,
,  ,
,  . Let u1 = (-1, 0) u2 = (0, 1), y1 = (0, 0) and y2 = (1, 0). Let
. Let u1 = (-1, 0) u2 = (0, 1), y1 = (0, 0) and y2 = (1, 0). Let , and
, and . Let
. Let and
and . Then,
. Then,  , i = 1, 2,
, i = 1, 2,  , i = 1, 2,
, i = 1, 2,  , j = 1, 2,
, j = 1, 2,  , k = 1, 2, and
, k = 1, 2, and , k = 1, 2. Moreover,
, k = 1, 2. Moreover,

and

Thus, Theorem 3.2 holds.
(2) Let . Then,
. Then,  is a weakly ε-efficient solution of (MFP)2, but not an ε-efficient solution of (MFP)2. Let
is a weakly ε-efficient solution of (MFP)2, but not an ε-efficient solution of (MFP)2. Let . Then, clB = cone co{(0, -1, -1), (1, 0, 0), (0, 0, 1)}. However, (1, 0, 0) ∉ B. Thus, B is not closed. Moreover,
. Then, clB = cone co{(0, -1, -1), (1, 0, 0), (0, 0, 1)}. However, (1, 0, 0) ∉ B. Thus, B is not closed. Moreover, ,
,  . Let
. Let and
and . Then,
. Then, and
and . Let μ1 = 1, μ2 = 0, α1 = β1 = α2 = β2 = 0 and
. Let μ1 = 1, μ2 = 0, α1 = β1 = α2 = β2 = 0 and  . Let
. Let ,
,  ,
,  ,
,  , n ∈ ℕ. Then,
, n ∈ ℕ. Then, ,
,  ,
,  ,
,  ,
,  . Let u1 = (-1, 0) and u2 = y1 = y2 = (0, 0). Then,
. Let u1 = (-1, 0) and u2 = y1 = y2 = (0, 0). Then, ,
,  ,
,  ,
,  . Let
. Let and
and . Then,
. Then, and
and . Thus,
. Thus,  ,
,  and
and . Hence, Theorem 3.4 holds.
. Hence, Theorem 3.4 holds.
References
Jeyakumar V, Lee GM, Dinh N: New sequential Lagrange multiplier conditions characterizing optimality without constraint qualification for convex programs. SIAM J Optim 2003,14(2):534–547.
Jeyakumar V, Wu ZY, Lee GM, Dinh N: Liberating the subgradient optimality conditions from constraint qualification. J Global Optim 2006,36(1):127–137.
Kim GS, Lee GM: On ε -approximate solutions for convex semidefinite optimization problems. Taiwanese J Math 2007,11(3):765–784.
Lee GM, Lee JH: ε -Duality theorems for convex semidefinite optimization problems with conic constraints. J Inequal 2010, 13. Art. ID363012
Kim GS, Lee GM: On ε -optimality theorems for convex vector optimization problems. To appear in Journal of Nonlinear and Convex Analysis
Govil MG, Mehra A: ε -Optimality for multiobjective programming on a Banach space. Eur J Oper Res 2004,157(1):106–112.
Gutiárrez C, Jimá B, Novo V: Multiplier rules and saddle-point theorems for Helbig's approximate solutions in convex Pareto problems. J Global Optim 2005,32(3):367–383.
Hamel A: An ε -Lagrange multiplier rule for a mathematical programming problem on Banach spaces. Optimization 2001,49(1–2):137–149.
Liu JC: ε -Duality theorem of nondifferentiable nonconvex multiobjective programming. J Optim Theory Appl 1991,69(1):153–167.
Liu JC: ε -Pareto optimality for nondifferentiable multiobjective programming via penalty function. J Math Anal Appl 1996,198(1):248–261.
Loridan P: Necessary conditions for ε -optimality. Optimality and stability in mathematical programming. Math Program Stud 1982, 19: 140–152.
Loridan P: ε -Solutions in vector minimization problems. J Optim Theory Appl 1984,43(2):265–276.
Strodiot JJ, Nguyen VH, Heukemes N: ε -Optimal solutions in nondifferentiable convex programming and some related questions. Math Program 1983,25(3):307–328.
Yokoyama K: Epsilon approximate solutions for multiobjective programming problems. J Math Anal Appl 1996,203(1):142–149.
Yokoyama K, Shiraishi S: ε -Necessary conditions for convex multiobjective programming problems without Slater's constraint qualification. , in press.
Hiriart-Urruty JB, Lemarechal C: Convex Analysis and Minimization Algorithms, vols. I and II. Springer-Verlag, Berlin; 1993.
Rockafellar RT: Convex Analysis. Princeton University Press, Princeton, NJ; 1970.
Zalinescu C: Convex Analysis in General Vector Space. World Scientific Publishing Co. Pte. Ltd, Singapore; 2002.
Jeyakumar V: Asymptotic dual conditions characterizing optimality for convex programs. J Optim Theory Appl 1997,93(1):153–165.
Jeyakumar V, Lee GM, Dinh N: Characterizations of solution sets of convex vector minimization problems. Eur. J Oper Res 2006,174(3):1380–1395.
Sawaragi Y, Nakayama H, Tanino T: Theory of Multiobjective Optimization. Academic Press, New York; 1985.
Gupta P, Shiraishi S, Yokoyama K: ε -Optimality without constraint qualification for multiobjective fractional problem. J Nonlinear Convex Anal 2005,6(2):347–357.
Acknowledgements
This study was supported by the Korea Science and Engineering Foundation (KOSEF) NRL program grant funded by the Korea government(MEST)(No. ROA-2008-000-20010-0).
Author information
Authors and Affiliations
Corresponding author
Additional information
4 Competing interests
The authors declare that they have no competing interests.
5 Authors' contributions
The authors, together discussed and solved the problems in the manuscript. All Authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, M.H., Kim, G.S. & Lee, G.M. On ε-optimality conditions for multiobjective fractional optimization problems. Fixed Point Theory Appl 2011, 6 (2011). https://doi.org/10.1186/1687-1812-2011-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-6
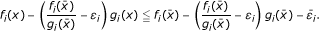
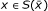 ; that is, there does not exist x
; that is, there does not exist x 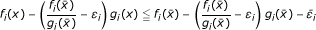
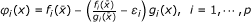 . Then, φ
i
(x), i = 1,
. Then, φ
i
(x), i = 1,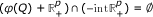 , and hence, it follows from separation theorem that there exist
, and hence, it follows from separation theorem that there exist 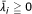 , i = 1, ..., p,
, i = 1, ..., p,  such that
such that 
 .
.