- Review
- Open access
- Published:
Fixed point theorems for multivalued contractive mappings and multivalued Caristi type mappings in cone metric spaces
Fixed Point Theory and Applications volume 2012, Article number: 133 (2012)
Abstract
In this paper, we establish a fixed-point theorem for multivalued contractive mappings in complete cone metric spaces. We generalize Caristi’s fixed-point theorem to the case of multivalued mappings in complete cone metric spaces. We give examples to support our main results. Our results are extensions of the results obtained by Feng and Liu (J. Math. Anal. Appl. 317:103-112, 2006) to the case of cone metric spaces.
MSC:47H10, 54H25.
1 Introduction
Banach’s contraction principle plays an important role in several branches of mathematics. Because of its importance for mathematical theory, it has been extended in many directions (see [10, 11, 14, 19, 21, 37, 46]); especially, the authors [36, 37, 39] generalized Banach’s principle to the case of multivalued mappings. Feng and Liu gave a generalization of Nadler’s fixed-point theorem. They proved the following theorem in [21].
Theorem 1.1 Let be a complete metric space and let be a multivalued map such that Tx is a closed subset of X for all . Let , where .
If there exists a constant such that for any , there exists satisfying
then T has a fixed point in X, i.e., there exists such that provided and the function , is lower semicontinuous.
Recently, in [22], the authors used the notion of a cone metric space to generalize the Banach contraction principle to the case of cone metric spaces. Since then, many authors [1–3, 7, 9, 13, 15, 18, 22–28, 32–34, 41, 43, 44, 48] obtained fixed-point theorems in cone metric spaces. The cone Banach space was first used in [4, 6]. Since then, the authors [29, 30] obtained fixed-point results in cone Banach spaces. The authors [8] proved a Caristi-type fixed-point theorem for single valued maps in cone metric spaces. The author [5] studied the structure of cone metric spaces.
Especially, the authors [16, 31, 35, 42, 45, 47] proved fixed point theorems for multivalued maps in cone metric spaces.
In this paper, we give a generalization of Theorem 1.1 to the case of cone metric spaces and we establish a Caristi-type fixed-point theorem for multivalued maps in cone metric spaces.
Consistent with Huang and Zhang [22], the following definitions will be needed in the sequel.
Let E be a topological vector space. A subset P of E is a cone if the following conditions are satisfied:
-
(1)
P is nonempty, closed, and ,
-
(2)
, whenever and
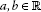 (),
(), -
(3)
.
Given a cone , we define a partial ordering ⪯ with respect to P by if and only if . We write to indicate that but .
For , stand for , where is the interior of P.
If E is a normed space, a cone P is called normal whenever there exists a number such that for all , implies .
A cone P is minihedral [20] if exists for all . A cone P is strongly minihedral [20] if every upper bounded nonempty subset A of E, supA exists in E. Equivalently, a cone P is strongly minihedral if every lower bounded nonempty subset A of E, infA exists in E (see also [1, 8]).
If E is a normed space, a strongly minihedral cone P is continuous whenever, for any bounded chain , and .
From now on, we assume that E is a normed space, is a solid cone (that is, ), and ⪯ is a partial ordering with respect to P.
Let X be a nonempty set. A mapping is called cone metric [22] on X if the following conditions are satisfied:
-
(1)
for all and if and only if ,
-
(2)
for all ,
-
(3)
for all .
Let be a cone metric space, and let be a sequence. Then
is convergent [22] to a point (denoted by or ) if for any , there exists N such that for all , .
is Cauchy [22] if for any , there exists N such that for all , . A cone metric space is called complete [22] if every Cauchy sequence is convergent.
Remark 1.1 (1) If , then . The converse is true if E is a normed space and P is a normal cone.
-
(2)
If , then is a Cauchy sequence in X. If E is a normed space and P is a normal cone, then is a Cauchy sequence in X if and only if .
We denote by (resp. , , ) the set of nonempty (resp. bounded, closed, closed and bounded) subsets of a cone metric space or a metric space.
The following definitions are found in [16].
Let for , and for and .
For , we denote
Lemma 1.1 ([16])
Let be a cone metric space, and let be a cone.
-
(1)
Let . If , then .
-
(2)
Let and . If , then .
-
(3)
Let and let and . If , then .
Remark 1.2 Let be a cone metric space. If  and , then is a metric space. Moreover, for , is the Hausdorff distance induced by d.
and , then is a metric space. Moreover, for , is the Hausdorff distance induced by d.
Remark 1.3 Let be a cone metric space. Then for .
If with , then for each there exists N such that for all .
2 Fixed-point theorems for multivalued contractive mappings
Let be a cone metric space, and let .
A function defined by is called sequentially lower semicontinuous if for any , there exists  such that for all , whenever for any sequence and .
such that for all , whenever for any sequence and .
Let be a multivalued mapping. We define a function as .
For a , let .
Theorem 2.1 Let be a complete cone metric space and let be a multivalued map. If there exists a constant such that for any there exists satisfying
then T has a fixed point in X provided and h is sequentially lower semicontinuous.
Proof Let . Then there exists such that . For , there exists such that .
Continuing this process, we can find a sequence such that
and
for all .
We now show that is a Cauchy sequence in X.
Since , .
From (2.2), we have . Thus, . Hence,
for all , where .
So we have
For , we have
By Lemma 1.2, is a Cauchy sequence in X. It follows from the completeness of X that there exists such that .
We now show that .
Suppose that .
Since Tz is closed, there exists such that implies .
But since h is sequentially lower semicontinuous, there exists N such that and .
Thus, there exists such that . Hence, , which is a contradiction. □
Remark 2.1 By Remark 1.1, Theorem 2.1 generalizes Theorem 1.1 ([12], Theorem 3.1]).
Corollary 2.2 Let be a complete cone metric space and let be a multivalued map. If there exists a constant such that for any ,
then T has a fixed point in X provided h is sequentially lower semicontinuous.
By Lemma 1.1(3), we have the following result, which is Nadler’s fixed-point theorem in the cone metric space.
Corollary 2.3 Let be a complete cone metric space, and let be a multivalued map. If there exists a constant , such that
for all , , then T has a fixed point in X provided h is sequentially lower semicontinuous.
By Remark 1.1, we have the following corollaries.
Corollary 2.4 ([21])
Let be a complete metric space and let be a multivalued map. If there exists a constant such that
for all , , then T has a fixed point in X provided h is sequentially lower semicontinuous.
Corollary 2.5 Let be a complete metric space and let be a multivalued map. If there exists a constant such that
for all , , then T has a fixed point in X provided h is sequentially lower semicontinuous.
The following example illustrates our main theorem.
Example 2.1 Let , and . Define by , where . Then d is a complete cone metric on X. Consider a mapping defined by
where is defined by .
Obviously, is sequentially lower semicontinuous.
For any , we can prove . To see this, we compute for
Since , we have , and hence we obtain .
Put . Then we have and for
Thus, we have , and .
Therefore, all conditions of Theorem 2.1 are satisfied and T has a fixed point .
3 Fixed-point theorems for multivalued Caristi type mappings
Let be a cone metric space with a preordering ⊑.
A sequence of points in X is called ⊑-decreasing if for all . The set is ⊑-complete if every decreasing Cauchy sequence in converges in it.
A function is called lower semicontinuous from above if, for every sequence conversing to some point and satisfying for all  , we have .
, we have .
Lemma 3.1 Let be a cone metric space, and let be a multivalued mapping. Suppose that is a function and is a nondecreasing, continuous, and subadditive function such that if and only if .
We define a relation on X as follows:
Then is a partial order on X.
Proof The proof follows by using the cone metric axioms, properties (2) and (3) for the cone, and (3.1). □
Lemma 3.2 ([17])
Let be a strongly minihedral and continuous cone, and let be a preordered set. Suppose that a mapping satisfies the following conditions:
-
(1)
and imply ;
-
(2)
for every ⊑-decreasing sequence , there exists such that for all
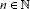 ;
; -
(3)
ψ is bounded from below.
Then, for each , has a minimal element in , where .
Theorem 3.1 Let be a cone metric space such that P is strongly minihedral and continuous, and let be a multivalued mapping and be a mapping bounded from below. Suppose that, for each , is -complete, where is a partial ordering on X defined as (3.1).
If for any , there exists satisfying
then T has a fixed point in X.
Proof We define a partial ordering on X as (3.1).
If and , then and , and so . Hence, .
Let be a -decreasing sequence in X. Then for all , and is bounded from below, because ϕ is bounded from below. Hence, is bounded. Since P is strongly minihedral, exists in E. Also, since P is continuous,  . Hence, and for all .
. Hence, and for all .
For , since , . Hence . Thus, . Since η is continuous, . So .
Hence, is a -decreasing Cauchy sequence in . Since is -complete and for all , there exists such that . Thus, for all .
By Lemma 3.2, has a minimal element in . By assumption, there exists such that . Hence, . Since is minimal element in , . Thus, . □
Corollary 3.2 Let be a cone metric space such that P is strongly minihedral and continuous, and let be a multivalued mapping and be a mapping bounded from below. Suppose that, for each , is -complete, where is a partial ordering on X defined as (3.1).
If for any and for any ,
then there exists such that .
Theorem 3.3 Let be a complete cone metric space such that P is strongly minihedral and continuous. Suppose that is a multivalued mapping and is lower semicontinuous from above and bounded from below.
If for any , there exists satisfying
then T has a fixed point in X.
Proof We define a partial ordering on X as (3.1). It suffices to show that, for each , is -complete.
Let be a fixed, and let be a -decreasing Cauchy sequence in . Then it is a -decreasing Cauchy sequence in X. Hence, for all 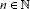 . Since X is complete, there exists such that . Since ϕ is lower semicontinuous from above, . Thus, for all
. Since X is complete, there exists such that . Since ϕ is lower semicontinuous from above, . Thus, for all 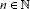 . Since for , we obtain
. Since for , we obtain
Hence,
Letting in above inequality, we have because η and d are continuous. Hence, .
Thus, we have , and so . Hence, , and hence is -complete. From Theorem 3.3, T has a fixed point in X. □
Corollary 3.4 Let be a complete cone metric space such that P is strongly minihedral and continuous. Suppose that is a multivalued mapping and is lower semicontinuous from above and bounded from below.
If for any and for any ,
then there exists such that .
We now give an example to support Theorem 3.3.
Example 3.1 Let , and let  and . We define by , where . Then is a complete cone metric space, and P is strongly minihedral and continuous.
and . We define by , where . Then is a complete cone metric space, and P is strongly minihedral and continuous.
Let for all .
We define a multivalued mapping by
and we define a mapping by
Then ϕ is lower semicontinuous from above and bounded from below.
For any , put . Then we have , and so .
Thus, all conditions of Theorem 3.3 are satisfied and T has a fixed point .
Remark 3.1 Theorem 3.3 (resp. Corollary 3.4) is a generalization of Theorem 4.2 (resp. Corollary 4.3) in [21], and also results in [38, 50] to the case of cone metric spaces.
If in Theorem 3.3 (resp. Corollary 3.4), then we have generalizations of the results in [12, 36, 49] to the case of cone metric spaces.
References
Alnafei SH, Radenović S, Shahzad N: Fixed point theorems for mappings with convex diminishing diameters on cone metric spaces. Appl. Math. Lett. 2011, 24: 2162–2166. 10.1016/j.aml.2011.06.019
Abbas M, Jungck G: Common fixed point results for noncommuting mappings without continuity in cone metric spaces. J. Math. Anal. Appl. 2008, 341: 416–420. 10.1016/j.jmaa.2007.09.070
Abbas M, Rhoades BE: Fixed and periodic point results in cone metric spaces. Appl. Math. Lett. 2008. doi:10.1016/j.akl.2008.07.001
Abdeljawad T: Completion of cone metric spaces. Hacet. J. Math. Stat. 2010, 39(1):67–74.
Abdeljawad T: Order norm completions of cone metric spaces. Numer. Funct. Anal. Optim. 2011, 32(5):477–495. 10.1080/01630563.2011.563892
Abdeljawad T, Türkoğlu D, Abuloha M: Some theorems and examples of cone Banach spaces. J. Comput. Anal. Appl. 2010, 12(4):739–753.
Abdeljawad T, Türkoğlu D: Locally convex valued rectangular metric spaces and the Kannan’s fixed point theorem. J. Comput. Anal. Appl. 2012, 14(3):484–494.
Abdeljawad T, Karapinar E: Quasicone metric spaces and generalizations of Caristi Kirk’s theorem. Fixed Point Theory Appl. 2009. doi:10.1155/2009/574387
Abdeljawad T, Murthy P, Taş K: A Gregus type common fixed point theorem of set-valued mappings in cone metric spaces. J. Comput. Anal. Appl. 2011, 13(4):622–628.
Agarwal RP, O’Regan DO, Shahzad N: Fixed point theorems for generalized contractive maps of Mei-Keeler type. Math. Nachr. 2004, 276: 3–12. 10.1002/mana.200310208
Aubin JP, Siegel J: Fixed point and stationary points of dissipative multi-valued maps. Proc. Am. Math. Soc. 1980, 78: 391–398. 10.1090/S0002-9939-1980-0553382-1
Aubin JP Grad. Texts in Math. In Optima and Equilibria. An Introduction to Nonlinear Analysis. Springer, Berlin; 1998.
Abdeljawad T, Karapinar E: A gap in the paper ‘A note on cone metric fixed point theory and its equivalence’ [Nolinear Analysis 72(5), (2010), 2259–2261]. Gazi Univ. J. Sci. 2011, 24(2):233–234.
Branciari A: A fixed point theorem for mappings satisfying a general contractive condition of integral type. Int. J. Math. Math. Sci. 2002, 29: 531–536. 10.1155/S0161171202007524
Cho SH, Bae JS: Common fixed point theorems for mappings satisfying property (E.A) on cone metric spaces. Math. Comput. Model. 2011, 53: 945–951. 10.1016/j.mcm.2010.11.002
Cho SH, Bae JS: Fixed point theorems for multivalued maps in cone metric spaces. Fixed Point Theory Appl. 2011., 2011: Article ID 87
Cho SH, Bae JS: Variational principles on cone metric spaces. Int. J. Pure Appl. Math. 2012, 77(5):709–718.
Choudhury BS, Metiya N: Fixed points of weak contractions in cone metric spaces. Nonlinear Anal. 2009. doi:10.1016/j.na.2009.08.040
Covitz H, Nadler SB Jr.: Multi-valued contraction mappings in generalized metric spaces. Isr. J. Math. 1970, 8: 5–11. 10.1007/BF02771543
Deimling K: Nonlinear Functional Analysis. Springer, Berlin; 1985.
Feng Y, Liu S: Fixed point theorems for multi-valued contractive mappings and multi-valued Caristi type mappings. J. Math. Anal. Appl. 2006, 317: 103–112. 10.1016/j.jmaa.2005.12.004
Huang LG, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. J. Math. Anal. Appl. 2007, 332(2):1468–1476. 10.1016/j.jmaa.2005.03.087
Ilić D, Rakočević V: Common fixed points for maps on cone metric spaces. J. Math. Anal. Appl. 2008, 341: 876–882. 10.1016/j.jmaa.2007.10.065
Ilić D, Rakočević V: Quasi-contraction on cone metric spaces. Appl. Math. Lett. 2008. doi:10.1016/j.aml.2008.08.001
Jungck G, Radenović S, Radojević S, Rakočević V: Common fixed point theorems for weakly compatible pairs on cone metric spaces. Fixed Point Theory Appl. 2009., 2009: Article ID 643840. doi:10.1155/2009/643840
Janković S, Kadelburg Z, Radenović S: On cone metric spaces. A survey. Nonlinear Anal. 2011, 74: 2591–2601. 10.1016/j.na.2010.12.014
Karapinar E: Some nonunique fixed point theorems of Ćirić type on cone metric spaces. Abstr. Appl. Anal. 2010., 2010: Article ID 123094. doi:10.1155/2010/123094
Karapinar E: Couple fixed point theorems for nonlinear contractions in cone metric spaces. Comput. Math. Appl. 2010, 59(12):3656–3668. 10.1016/j.camwa.2010.03.062
Karapinar E: Fixed point theorems in cone Banach spaces. Fixed Point Theory Appl. 2009., 2009: Article ID 609281. doi:10.1155/2009/609281
Karapinar E, Türkoğlu D: Best approximations theorem for a couple in cone Banach spaces. Fixed Point Theory Appl. 2010., 2010: Article ID 784578
Kadelburg Z, Radenović S: Some results on set-valued contractions in abstract metric spaces. Comput. Math. Appl. 2011, 62: 342–350. 10.1016/j.camwa.2011.05.015
Kadelburg Z, Radenović S, Rakočević V: Topological vector space-valued cone metric spaces and fixed point theorems. Fixed Point Theory Appl. 2010., 2010: Article ID 170253. doi:10.1155/2010/170253
Kadelburg Z, Radenović S, Rakočević V: A note on the equivalence of some metric and cone metric fixed point results. Appl. Math. Lett. 2011, 24: 370–374. 10.1016/j.aml.2010.10.030
Kadelburg Z, Radenović S, Rakočević V: Remarks on ’Quasi-contraction on a cone metric spaces’. Appl. Math. Lett. 2009, 22: 1674–1679. 10.1016/j.aml.2009.06.003
Klim D, Wardowski D: Dynamic processes and fixed points of set-valued nonlinear contractions in cone metric spaces. Nonlinear Anal. 2009, 71: 5170–5175. 10.1016/j.na.2009.04.001
Mizoguchi N, Takahashi W: Fixed point theorems for multi-valued mappings on complete metric spaces. J. Math. Anal. Appl. 1989, 141: 177–188. 10.1016/0022-247X(89)90214-X
Nadler SB Jr.: Multi-valued contraction mappings. Pac. J. Math. 1969, 30: 475–478. 10.2140/pjm.1969.30.475
Naidu SVR: Fixed-point theorems for a broad class of multimaps. Nonlinear Anal. 2003, 52: 961–969. 10.1016/S0362-546X(02)00146-3
Reich S: Some problems and results in fixed point theory. Contemp. Math. 1983, 21: 179–187.
Dordević M, Dorić D, Kadelburg Z, Radenović S, Spasić D: Fixed point results under c -distance in tvs-cone metric spaces. Fixed Point Theory Appl. 2011., 2011: Article ID 29. doi:10.1186/1687–1812–2011–29
Rezapour S, Hamlbarani R: Some notes on the paper ‘Cone metric spaces and fixed point theorems of contractive mappings’. J. Math. Anal. Appl. 2008, 345: 719–724. 10.1016/j.jmaa.2008.04.049
Radenović S, Kadelburg Z: Some results on fixed points of multifunctions on abstract metric spaces. Math. Comput. Model. 2011, 53: 746–754. 10.1016/j.mcm.2010.10.012
Radenović S, Simić S, Cakić N, Golubović Z: A note on tvs-cone metric fixed point theory. Math. Comput. Model. 2011, 54: 2418–2422. 10.1016/j.mcm.2011.05.051
Türkoğlu D, Abuloha M, Abdeljawad T: Fixed points of generalized contraction mappings in cone metric spaces. Math. Commun. 2011, 16: 325–334.
Türkoğlu D, Abuloha M, Abdeljawad T: KKM mappings in cone metric spaces and some fixed point theorems. Nonlinear Anal., Theory Methods Appl. 2010, 72(1):348–353. 10.1016/j.na.2009.06.058
Wang T: Fixed point theorems and fixed point stability for multivalued mappings on metric spaces. J. Nanjing Univ., Math. Biq. 1989, 6: 16–23.
Wardowski D: Endpoints and fixed points of set-valued contractions in cone metric spaces. Nonlinear Anal. 2009, 71: 512–516. 10.1016/j.na.2008.10.089
Yang SK, Bae JS, Cho SH: Coincidence and common fixed and periodic point theorems in cone metric spaces. Comput. Math. Appl. 2011, 61: 170–177. 10.1016/j.camwa.2010.10.031
Zhang SS, Luo Q: Set-valued Caristi fixed point theorem and Ekeland’s variational principle. Appl. Math. Mech. 1989, 10(2):111–113. (in Chinese). English translation: Appl. Math. Mech., Engl. Ed. 10(2), 119–121 (1989)
Zhong CK, Zhu J, Zhao PH: An extension of multi-valued contraction mappings and fixed points. Proc. Am. Math. Soc. 2000, 128: 2439–2444. 10.1090/S0002-9939-99-05318-6
Acknowledgements
The authors would like to thank the referees for careful reading and giving valuable comments. This research (S.H. Cho) was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science, and Technology (No. 2011-0012118).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cho, SH., Bae, JS. & Na, KS. Fixed point theorems for multivalued contractive mappings and multivalued Caristi type mappings in cone metric spaces. Fixed Point Theory Appl 2012, 133 (2012). https://doi.org/10.1186/1687-1812-2012-133
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2012-133
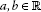 (),
(),