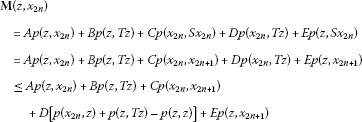Fixed point theorems under Hardy-Rogers contractive conditions on 0-complete ordered partial metric spaces

Abstract

A fixed point theorem is obtained for a monotone self-map in a 0-complete ordered partial metric space under Hardy-Rogers-type contractive condition. This result improves some recently obtained ones, in the sense that weaker conditions are used. An example shows how this result can be used when the corresponding result in standard metric cannot. The second theorem is concerned with two weakly isotone increasing self-mappings in ordered partial metric spaces. A common fixed point result is obtained without any commutativity or compatibility assumptions.

MSC:47H10, 54H25.

1 Introduction

Matthews [1] introduced the notion of a partial metric space as a part of the study of denotational semantics of dataflow networks. He showed that the Banach contraction mapping theorem can be generalized to the partial metric context for applications in program verification. Subsequently, several authors (see, e.g., [2–12]) derived fixed point theorems in partial metric spaces. See also the presentation by Bukatin et al. [13] where the motivation for introducing non-zero distance (i.e., the ‘distance’ p where $p(x,x)=0$ need not hold) is explained, which is also leading to interesting research in foundations of topology.

On the other hand, fixed point theory has developed rapidly in partially ordered metric spaces. The first result in this direction was given by Ran and Reurings [14] who presented its applications to matrix equations. Subsequently, Nieto and Rodríguez-López [15] extended this result and applied it to obtain a unique solution for periodic boundary value problems. Further results were obtained by several authors, we mention [16–21]. Fixed point results in ordered partial metric spaces have been obtained recently in [22–26].

The following definitions and details can be seen in [1–4] and [13, 27, 28].

Definition 1.1 A partial metric on a nonempty set X is a function $p:X\times X\to {\mathbb{R}}^{+}$ such that for all $x,y,z\in X$,

(p₁) $x=y⟺p(x,x)=p(x,y)=p(y,y)$,

(p₂) $p(x,x)\le p(x,y)$,

(p₃) $p(x,y)=p(y,x)$,

(p₄) $p(x,y)\le p(x,z)+p(z,y)-p(z,z)$.

The pair $(X,p)$ is called a partial metric space.

It is clear that if $p(x,y)=0$, then from (p₁) and (p₂) $x=y$. But if $x=y$, $p(x,y)$ may not be 0.

Each partial metric p on X generates a $T_0$ topology ${\tau }_p$ on X which has as a base the family of open p-balls $\{B_p(x,\epsilon ):x\in X,\epsilon >0\}$, where $B_p(x,\epsilon )=\{y\in X:p(x,y)<p(x,x)+\epsilon \}$ for all $x\in X$ and $\epsilon >0$. A sequence $\{x_n\}$ in $(X,p)$ converges to a point $x\in X$ (in the sense of ${\tau }_p$) if ${lim}_{n\to \mathrm{\infty }}p(x,x_n)=p(x,x)$. This will be denoted as $x_n\to x$ ($n\to \mathrm{\infty }$) or ${lim}_{n\to \mathrm{\infty }}{x}_n=x$.

Remark 1.2 Clearly, a limit of a sequence in a partial metric space need not be unique. Moreover, the function $p(\cdot ,\cdot )$ need not be continuous in the sense that $x_n\to x$ and $y_n\to y$ imply $p(x_n,y_n)\to p(x,y)$.

If p is a partial metric on X, then the function $p^s:X\times X\to {\mathbb{R}}^{+}$ given by

$$p^s(x,y)=2p(x,y)-p(x,x)-p(y,y)$$

(1.1)

is a metric on X. Furthermore, ${lim}_{n\to \mathrm{\infty }}{p}^s(x_n,x)=0$ if and only if

$$p(x,x)=\underset{n\to \mathrm{\infty }}{lim}p(x_n,x)=\underset{n,m\to \mathrm{\infty }}{lim}p(x_n,x_m).$$

Example 1.3

• (1) A paradigmatic example of a partial metric space is the pair $({\mathbb{R}}^{+},p)$, where $p(x,y)=max\{x,y\}$ for all $x,y\in {\mathbb{R}}^{+}$. The corresponding metric is

  $$p^s(x,y)=2max\{x,y\}-x-y=|x-y|.$$

• (2) If $(X,d)$ is a metric space and $c\ge 0$ is arbitrary, then

  $$p(x,y)=d(x,y)+c$$

defines a partial metric on X and the corresponding metric is $p^s(x,y)=2d(x,y)$.

Remark 1.4 If $T:X\to X$ is continuous at $x_0\in X$ (with respect to ${\tau }_p$), then for each sequence $\{x_n\}$ in X, we have

(1.2)

It is worth mentioning that the notions of p-continuity and $p^s$-continuity for a self-mapping on X are incomparable in general. Indeed, let $X=[0,+\mathrm{\infty })$, $p(x,y)=max\{x,y\}$ (and hence $p^s(x,y)=|x-y|$), $T0=1$, $Tx=x^2$ for $x>0$, and let $Sx=|sinx|$. Then it is easy to see that T is p-continuous and $p^s$-discontinuous at $x=0$, while S is p-discontinuous and $p^s$-continuous at $x=\pi$ (for details, see [29]).

Other examples of partial metric spaces which are interesting from the computational point of view may be found in [1, 30, 31].

Definition 1.5 Let $(X,p)$ be a partial metric space. Then:

• (1) A sequence $\{x_n\}$ in $(X,p)$ is called a Cauchy sequence if ${lim}_{n,m\to \mathrm{\infty }}p(x_n,x_m)$ exists (and is finite).

• (2) The space $(X,p)$ is said to be complete if every Cauchy sequence $\{x_n\}$ in X converges, with respect to ${\tau }_p$, to a point $x\in X$ such that $p(x,x)={lim}_{n,m\to \mathrm{\infty }}p(x_n,x_m)$.

• (3) [28] A sequence $\{x_n\}$ in $(X,p)$ is called 0-Cauchy if ${lim}_{n,m\to \mathrm{\infty }}p(x_n,x_m)=0$. The space $(X,p)$ is said to be 0-complete if every 0-Cauchy sequence in X converges (in ${\tau }_p$) to a point $x\in X$ such that $p(x,x)=0$.

Lemma 1.6 Let $(X,p)$ be a partial metric space.

• (a) $\{x_n\}$ is a Cauchy sequence in $(X,p)$ if and only if it is a Cauchy sequence in the metric space $(X,p^s)$.

• (b) The space $(X,p)$ is complete if and only if the metric space $(X,p^s)$ is complete.

• (c) [5, 9]If $p(x_n,z)\to p(z,z)=0$ as $n\to \mathrm{\infty }$, then $p(x_n,y)\to p(z,y)$ as $n\to \mathrm{\infty }$ for each $y\in X$.

• (d) Every 0-Cauchy sequence in $(X,p)$ is Cauchy in $(X,p^s)$.

• (e) If $(X,p)$ is complete, then it is 0-complete.

The converse assertions of (d) and (e) do not hold as the following easy example shows.

Example 1.7 [28] The space $X=[0,+\mathrm{\infty })\cap \mathbb{Q}$ with the partial metric $p(x,y)=max\{x,y\}$ is 0-complete, but it is not complete (since $p^s(x,y)=|x-y|$ and $(X,p^s)$ is not complete). Moreover, the sequence $\{x_n\}$ with $x_n=1$ for each $n\in \mathbb{N}$ is a Cauchy sequence in $(X,p)$, but it is not a 0-Cauchy sequence.

Recall that Romaguera proved in [[28], Theorem 2.3] that a partial metric space $(X,p)$ is 0-complete if and only if every $p^s$-Caristi mapping on X has a fixed point.

It is easy to see that every closed subset of a 0-complete partial metric space is 0-complete.

Definition 1.8 Let $(X,⪯)$ be a partially ordered set. Then:

• (a) elements $x,y\in X$ are called comparable if $x⪯y$ or $y⪯x$ holds;

• (b) a subset K of X is said to be well ordered if every two elements of K are comparable;

• (c) a mapping $T:X\to X$ is called nondecreasing (nonincreasing) w.r.t. ⪯ if $x⪯y$ implies $Tx⪯Ty$ ($Tx⪰Ty$).

Definition 1.9 Let X be a nonempty set. Then $(X,p,⪯)$ is called an ordered (partial) metric space if:

• (i) $(X,p)$ is a (partial) metric space, and

• (ii) $(X,⪯)$ is a partially ordered set.

Definition 1.10 Let $(X,p,⪯)$ be an ordered partial metric space. We say that X is regular if the following holds: if $\{z_n\}$ is a nondecreasing (resp. nonincreasing) sequence in X with respect to ⪯ such that $z_n\to z\in X$ as $n\to \mathrm{\infty }$, then $z_n⪯z$ (resp. $z_n⪰z$) for all $n\in \mathbb{N}$.

In this paper, we first obtain a fixed point theorem for a monotone self-map in a 0-complete partially ordered partial metric space under Hardy-Rogers-type contractive condition. This result improves some recently obtained ones, in particular those from [26], in the sense that weaker conditions are used. It can be also considered as an extension and improvement of some results in standard ordered metric spaces, e.g., those from [20]. An example shows that our theorem can be used when the corresponding result in standard metric cannot.

The second theorem is concerned with two weakly isotone increasing self-mappings in ordered partial metric spaces and is related to the results of the paper [25]. A common fixed point result is obtained without commutativity or compatibility assumptions. An example shows how this theorem can be used.

2 Fixed point results for a single mapping

Our first result is the following

Theorem 2.1 Let $(X,p,⪯)$ be a 0-complete ordered partial metric space. Let $T:X\to X$ be a nondecreasing (nonincreasing) mapping such that

$$p(Tx,Ty)\le \mathbf{M}(x,y)$$

(2.1)

for all comparable $x,y\in X$, where

$$\mathbf{M}(x,y)=Ap(x,y)+Bp(x,Tx)+Cp(y,Ty)+Dp(y,Tx)+Ep(x,Ty),$$

(2.2)

$A,B,C,D,E\ge 0$ and $A+B+C+D+E<1$. Also suppose that there exists $x_0\in X$ with $x_0⪯T{x}_0$ (resp. $x_0⪰T{x}_0$). We suppose the following:

• (i) T is continuous, or

• (ii) X is regular.

Then T has a fixed point z and $p(Tz,Tz)=0=p(z,z)$. Moreover, the set $F(T)$ of fixed points of T is well ordered if and only if it is a singleton.

Proof We will prove the theorem for the case of a nondecreasing mapping. Starting from the given element $x_0\in X$, form the sequence $\{x_n\}$ as $x_n=T{x}_{n-1}$, $n\in \mathbb{N}$. If $p(x_n,x_{n+1})=0$ for some $n\ge 0$, then $T{x}_n=x_{n+1}=x_n$ and $p(x_n,x_n)=0$ (by (p₂)) and the proof is completed. Suppose further that $p(x_n,x_{n+1})>0$ for all $n\ge 0$. Note that, since T is nondecreasing, we have that

$$x_0⪯T{x}_0=x_1⪯T{x}_1=x_2⪯\dots ⪯x_n⪯T{x}_n=x_{n+1}⪯\cdots .$$

Applying condition (2.1) to comparable elements $x=x_n$ and $y=x_{n+1}$, we get that

$$\begin{array}{rcl}p(x_{n+1},x_{n+2})& =& p(T{x}_n,T{x}_{n+1})\le \mathbf{M}(x_n,x_{n+1})\\ =& Ap(x_n,x_{n+1})+Bp(x_n,x_{n+1})+Cp(x_{n+1},x_{n+2})\\ +Dp(x_{n+1},x_{n+1})+Ep(x_n,x_{n+2})\\ \le & (A+B+E)p(x_n,x_{n+1})+(C+E)p(x_{n+1},x_{n+2})\\ +(D-E)p(x_{n+1},x_{n+1})\text{by (p}{}_4\text{)}.\end{array}$$

(2.3)

Similarly, applying (2.1) with $x=x_{n+1}$ and $y=x_n$, we get

$$\begin{array}{rcl}p(x_{n+2},x_{n+1})& =& p(T{x}_{n+1},T{x}_n)\le \mathbf{M}(x_{n+1},x_n)\\ =& Ap(x_{n+1},x_n)+Bp(x_{n+1},x_{n+2})+Cp(x_n,x_{n+1})\\ +Dp(x_n,x_{n+2})+Ep(x_{n+1},x_{n+1})\\ \le & (A+C+D)p(x_n,x_{n+1})+(B+D)p(x_{n+1},x_{n+2})\\ +(E-D)p(x_{n+1},x_{n+1})\text{by (p}{}_4\text{)}.\end{array}$$

(2.4)

Adding up (2.3) and (2.4), we obtain

$$p(x_{n+1},x_{n+2})\le \lambda p(x_n,x_{n+1}),$$

with

$$0\le \lambda =\frac{2A+B+C+D+E}{2-(B+C+D+E)}<1,$$

since $A+B+C+D+E<1$. It follows that $p(x_n,x_{n+1})\le {\lambda }^{n}p(x_0,x_1)$ and ${lim}_{n\to \mathrm{\infty }}p(x_n,x_{n+1})=0$. Also, for $n>m$,

$$p(x_n,x_m)\le ({\lambda }^m+\cdots +{\lambda }^{n-1})p(x_0,x_1),$$

and hence ${lim}_{m,n\to \mathrm{\infty }}p(x_n,x_m)=0$. Hence, $\{x_n\}$ is a 0-Cauchy sequence in $(X,p)$. Since $(X,p)$ is 0-complete, it follows that there exists $z\in X$ such that $x_n\to z$ in $(X,p)$ and $p(z,z)=0$. Moreover,

$$\underset{n\to \mathrm{\infty }}{lim}p(x_n,z)=p(z,z)=0.$$

(2.5)

We will prove that $Tz=z$.

• (i) Suppose that T is continuous. Letting $n\to \mathrm{\infty }$ in

  $$p(z,Tz)\le p(z,x_{n+1})+p(x_{n+1},Tz)-p(x_{n+1},x_{n+1})\le p(z,x_{n+1})+p(x_{n+1},Tz)$$

and applying (2.5) and (1.2), we get

$$\begin{array}{rl}p(z,Tz)& \le \underset{n\to \mathrm{\infty }}{lim}p(z,x_{n+1})+\underset{n\to \mathrm{\infty }}{lim}p(T{x}_n,Tz)\\ =p(z,z)+p(Tz,Tz)=p(Tz,Tz).\end{array}$$

Thus, we have $p(z,Tz)\le p(Tz,Tz)$. But from (p₂), we have $p(Tz,Tz)\le p(z,Tz)$. Hence,

$$p(z,Tz)=p(Tz,Tz).$$

Suppose that $p(z,Tz)>0$. Now, since $z⪯z$, by inequality (2.1) we have

$$\begin{array}{rl}p(z,Tz)& =p(Tz,Tz)\le \mathbf{M}(z,z)=(B+C+D+E)p(z,Tz)\\ \le (A+B+C+D+E)p(z,Tz)<p(z,Tz),\end{array}$$

which is a contradiction. Thus, we get that $p(Tz,Tz)=p(z,Tz)=p(z,z)=0$. By (p₁), we conclude that $z=Tz$, that is, z is a fixed point of T.

• (ii) Suppose now that the space X is regular. Substituting $x=x_n$ and $y=z$ (these elements are comparable) in the contractive condition (2.1), we get

  $$\begin{array}{rl}p(x_{n+1},Tz)& =p(T{x}_n,Tz)\\ \le Ap(x_n,z)+Bp(x_n,x_{n+1})+Cp(z,Tz)+Dp(z,x_{n+1})+Ep(x_n,Tz).\end{array}$$

Passing to the limit as $n\to \mathrm{\infty }$, and using Lemma 1.6(c), we get that

$$p(z,Tz)\le (C+E)p(z,Tz)\le (A+B+C+D+E)p(z,Tz),$$

which is (because of $A+B+C+D+E<1$) possible only if $p(z,Tz)=0$. We conclude that $Tz=z$.

Now suppose that the set of fixed points of T is well ordered. We claim that the fixed point of T is unique. Assume to the contrary that $Tu=u$ and $Tv=v$, but $u\ne v$. By supposition, we can replace x by u and y by v in (2.1) to obtain

$$\begin{array}{rl}p(u,v)& =p(Tu,Tv)\le \mathbf{M}(u,v)\\ =Ap(u,v)+Bp(u,Tu)+Cp(v,Tv)+Dp(v,Tu)+Ep(u,Tv)\\ =Ap(u,v)+Bp(u,u)+Cp(v,v)+Dp(v,u)+Ep(u,v)\\ \le (A+B+C+D+E)p(u,v)<p(u,v),\end{array}$$

unless $p(u,v)=0$. Hence, $u=v$ and the fixed point of T is unique. The converse is trivial. Thus, the proof is complete. □

Remark 2.2 Note that this theorem improves [[26], Theorem 2.6 and Corollary 2.9] since our assumptions are weaker than the assumptions from [26] in several places: 1^∘ there is no need to use additional function ϕ, hence our contractive condition (2.1) is weaker than the one used in [26] (function ψ is redundant anyway, see e.g., [32]); 2^∘ conditions on coefficients A, B, C, D, E are weaker (just the usual Hardy-Rogers-type conditions); 3^∘ 0-completeness is used instead of completeness (see Lemma 1.6(e) and Example 1.7).

Similarly, putting $d=p$, we obtain an improvement of [[20], Theorem 5].

In a standard way, one gets the following corollary with integral-type condition (see [33]).

Corollary 2.3 Let all the conditions of Theorem 2.1 be fulfilled, except that the condition (2.1) is replaced by

$${\int }_0^{p(Tx,Ty)}\phi (t)dt\le {\int }_0^{\mathbf{M}(x,y)}\phi (t)dt$$

for all comparable $x,y\in X$, where $\mathbf{M}(x,y)$ is given by (2.2), and $\phi :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ is a nonnegative Lebesgue integrable function (with finite integral) on each compact subset of ${\mathbb{R}}^{+}$, satisfying ${\int }_0^{\epsilon }\phi (t)dt>0$ for each $\epsilon >0$.

We demonstrate the use of Theorem 2.1 with the help of the following example. It will also show that this theorem is more general than some other known fixed point results.

Example 2.4 Let $X=[0,+\mathrm{\infty })\cap \mathbb{Q}$ be endowed with the usual partial metric $p:X\times X\to [0,+\mathrm{\infty })$ defined by $p(x,y)=max\{x,y\}$. The partial metric space $(X,p)$ is 0-complete (see Example 1.7). We endow X with the partial order

$$x⪯y\iff x=y\text{or}\text{(}x,y\in [0,1]\text{ with }x\le y\text{)}.$$

Define $T:X\to X$ as

$$Tx=\{\begin{array}{cc}\frac{x^2}{1+x},\hfill & x\in [0,1],\hfill \\ \frac{x}{2},\hfill & x>1,\hfill \end{array}$$

and take $\mathbf{M}(x,y)=\frac{1}{2}p(x,y)$, i.e., $A=\frac{1}{2}$, $B=C=D=E=0$. Suppose that $y⪯x$. Then there are two possibilities. If $x\in [0,1]$ (and so $y\in [0,1]$), then

$$p(Tx,Ty)=max\{\frac{x^2}{1+x},\frac{y^2}{1+y}\}=\frac{x^2}{1+x}.$$

Since $\mathbf{M}(x,y)=\frac{1}{2}x$, it easily follows that $p(Tx,Ty)\le \mathbf{M}(x,y)$. If $x>1$ (and so $y=x$), then $p(Tx,Ty)=\frac{x}{2}=\mathbf{M}(x,y)$. Hence, in all possible cases, condition (2.1) holds. Also, it is clear that both the condition of regularity of X and continuity of T are satisfied, and for $x_0=0$, we have $x_0⪯T{x}_0$. Therefore, all conditions of Theorem 2.1 are satisfied, and so T has a fixed point in X (which is $z=0$).

On the other hand, consider the same problem in the standard metric $d(x,y)$ and take $x=1$ and $y=\frac{1}{2}$. Then $d(Tx,Ty)=|\frac{1}{2}-\frac{1}{6}|=\frac{1}{3}$ and $\mathbf{M}(x,y)=\frac{1}{2}d(1,\frac{1}{2})=\frac{1}{4}$ and so

$$\mathbf{M}(x,y)=\frac{1}{4}<\frac{1}{3}=d(Tx,Ty).$$

Hence, $d(Tx,Ty)\le \mathbf{M}(x,y)$ does not hold and the existence of a fixed point of T cannot be obtained from the known results in standard metric spaces.

3 Common fixed point results for a pair of weakly isotone increasing mappings

In this section, we give a common fixed point theorem for a pair of maps satisfying T-weakly isotone increasing property. For this we need the following definitions.

Definition 3.1 Let $(X,⪯)$ be a partially ordered set, and let $S,T:X\to X$ be two mappings.

• (1) [34] The pair $(S,T)$ is said to be weakly increasing if $Sx⪯TSx$ and $Tx⪯STx$ for all $x\in X$.

• (2) [21] The mapping S is said to be T-weakly isotone increasing if for all $x\in X$ we have $Sx⪯TSx⪯STSx$.

Remark 3.2 Note that two weakly increasing mappings need not be nondecreasing. There exist some examples to illustrate this fact in [19].

If $S,T:X\to X$ are weakly increasing, then S is T-weakly isotone increasing.

Theorem 3.3 Let $(X,p,⪯)$ be a 0-complete ordered partial metric space. Let $S,T:X\to X$ be two mappings such that S is T-weakly isotone increasing and satisfying

$$p(Tx,Sy)\le \mathbf{M}(x,y)$$

(3.1)

for all comparable $x,y\in X$, where

$$\mathbf{M}(x,y)=Ap(x,y)+Bp(x,Tx)+Cp(y,Sy)+Dp(y,Tx)+Ep(x,Sy),$$

(3.2)

$A,B,C,D,E\ge 0$, $A+B+C+D+2E<1$ and $A+B+C+2D+E<1$. We suppose the following:

• (i) S and T are continuous or

• (ii) X is regular.

Then S and T have a common fixed point z and

$$p(z,z)=p(Tz,Tz)=p(Sz,Sz)=p(z,Sz)=p(z,Tz)=0.$$

(3.3)

Moreover, the set of common fixed points of T and S is well ordered if and only if T and S have one and only one common fixed point.

Remark 3.4 Note that in this result continuity of both mappings is crucial (when the space is not regular); however, no compatibility of these mappings is needed.

Proof Let $x_0$ be an arbitrary point in X. If $p(x_0,S{x}_0)=0$ or $p(x_0,T{x}_0)=0$, the proof is finished. Indeed, suppose e.g., that $p(x_0,T{x}_0)=0$ (and hence $T{x}_0=x_0$). Then (3.1) implies that

$$\begin{array}{rcl}p(x_0,S{x}_0)& =& p(T{x}_0,S{x}_0)\le \mathbf{M}(x_0,x_0)\\ =& Ap(x_0,x_0)+(C+E)p(x_0,S{x}_0)\\ \le & (A+C+E)p(x_0,S{x}_0)<p(x_0,S{x}_0)\text{(by (p}{}_2\text{))}\end{array}$$

(since $A+C+E\le A+B+C+D+2E<1$) unless $p(x_0,S{x}_0)=0$, implying that $S{x}_0=x_0$. Thus, $x_0$ is a common fixed point of T and S and (3.3) holds with $z=x_0$.

Assume further that $p(x_0,S{x}_0)>0$ and $p(x_0,T{x}_0)>0$. We can define a sequence $\{x_n\}$ in X as follows:

$$x_{2n+1}=S{x}_{2n}\text{and}{x}_{2n+2}=T{x}_{2n+1}\text{for }n\in \{0,1,2,\dots \}.$$

Without loss of generality, we can suppose that $p(x_n,x_{n+1})>0$ for each $n\in \{0,1,2,\dots \}$. Otherwise we have again finished.

Note that, since S is T-weakly isotone increasing, we have

and continuing this process, we get

$$x_1⪯x_2⪯\cdots ⪯x_n⪯x_{n+1}⪯\cdots .$$

Now since $x=x_{2n-1}$ and $y=x_{2n}$ are comparable, we can use inequality (3.1) for these points, and we have

$$\begin{array}{rcl}p(x_{2n},x_{2n+1})& =& p(T{x}_{2n-1},S{x}_{2n})\le \mathbf{M}(x_{2n-1},x_{2n})\\ =& Ap(x_{2n-1},x_{2n})+Bp(x_{2n-1},T{x}_{2n-1})+Cp(x_{2n},S{x}_{2n})\\ +Dp(x_{2n},T{x}_{2n-1})+Ep(x_{2n-1},S{x}_{2n})\\ =& Ap(x_{2n-1},x_{2n})+Bp(x_{2n-1},x_{2n})+Cp(x_{2n},x_{2n+1})\\ +Dp(x_{2n},x_{2n})+Ep(x_{2n-1},x_{2n+1})\\ \le & Ap(x_{2n-1},x_{2n})+Bp(x_{2n-1},x_{2n})+Cp(x_{2n},x_{2n+1})\\ +Dp(x_{2n},x_{2n})+E[p(x_{2n-1},x_{2n})+p(x_{2n},x_{2n+1})-p(x_{2n},x_{2n})]\\ \le & (A+B+E)p(x_{2n-1},x_{2n})+(C+D+E)p(x_{2n},x_{2n+1})\text{(by (p}{}_2\text{))},\end{array}$$

wherefrom

$$p(x_{2n},x_{2n+1})\le \frac{A+B+E}{1-(C+D+E)}p(x_{2n-1},x_{2n}).$$

(3.4)

Similarly, using (3.1) with $x=x_{2n+1}$ and $y=x_{2n}$, we get that

$$\begin{array}{rcl}p(x_{2n+2},x_{2n+1})& =& p(T{x}_{2n+1},S{x}_{2n})\le \mathbf{M}(x_{2n+1},x_{2n})\\ =& Ap(x_{2n+1},x_{2n})+Bp(x_{2n+1},x_{2n+2})+Cp(x_{2n},x_{2n+1})\\ +Dp(x_{2n},x_{2n+2})+Ep(x_{2n+1},x_{2n+1})\\ \le & Ap(x_{2n+1},x_{2n})+Bp(x_{2n+1},x_{2n+2})+Cp(x_{2n},x_{2n+1})\\ +D[p(x_{2n},x_{2n+1})+p(x_{2n+1},x_{2n+2})-p(x_{2n+1},x_{2n+1})]+Ep(x_{2n+1},x_{2n+1})\\ \le & (A+C+D)p(x_{2n+1},x_{2n})+(B+D+E)p(x_{2n+1},x_{2n+2})\text{(by (p}{}_2\text{))},\end{array}$$

wherefrom

$$p(x_{2n+1},x_{2n+2})\le \frac{A+C+D}{1-(B+D+E)}p(x_{2n},x_{2n+1}).$$

(3.5)

It follows from (3.4) and (3.5) that

$$p(x_n,x_{n+1})\le \lambda p(x_{n-1},x_n),n\in \mathbb{N},$$

(3.6)

where

$$0\le \lambda =max\{\frac{A+B+E}{1-(C+D+E)},\frac{A+C+D}{1-(B+D+E)}\}<1$$

since $A+B+C+D+2E<1$ and $A+B+C+2D+E<1$. It follows from (3.6) that $p(x_n,x_{n+1})\le {\lambda }^{n}p(x_0,x_1)$ and ${lim}_{n\to \mathrm{\infty }}p(x_n,x_{n+1})=0$. Also, for $n>m$,

$$p(x_n,x_m)\le ({\lambda }^m+\dots +{\lambda }^{n-1})p(x_0,x_1),$$

and hence ${lim}_{m,n\to \mathrm{\infty }}p(x_n,x_m)=0$. Thus, $\{x_n\}$ is a 0-Cauchy sequence in $(X,p)$. Since $(X,p)$ is 0-complete, it follows that there exists $z\in X$ such that $x_n\to z$ in $(X,p)$ and $p(z,z)=0$. Moreover,

$$\underset{n\to \mathrm{\infty }}{lim}p(x_n,z)=p(z,z)=0.$$

(3.7)

We will prove that $Tz=Sz=z$.

By (p₄), we have

$$\begin{array}{rl}p(z,Tz)& \le p(z,x_{2n+2})+p(x_{2n+2},Tz)-p(x_{2n+2},x_{2n+2})\\ \le p(z,x_{2n+2})+p(x_{2n+2},Tz),\end{array}$$

(3.8)

and, similarly,

$$p(z,Tz)\le p(z,x_{2n+1})+p(x_{2n+1},Tz).$$

(3.9)

• (i) Suppose that T is continuous. Letting $n\to \mathrm{\infty }$ in (3.8) and applying (3.7), we get

  $$\begin{array}{rl}p(z,Tz)& \le \underset{n\to \mathrm{\infty }}{lim}p(z,x_{2n+2})+\underset{n\to \mathrm{\infty }}{lim}p(T{x}_{2n+1},Tz)\\ =p(Tz,Tz).\end{array}$$

Thus, we have $p(z,Tz)\le p(Tz,Tz)$. But from (p₂), we have $p(Tz,Tz)\le p(z,Tz)$. Hence,

$$p(z,Tz)=p(Tz,Tz).$$

(3.10)

Similarly, if S is continuous, we have

$$p(z,Sz)=p(Sz,Sz).$$

(3.11)

By (p₄) and using (3.11), we have

$$\begin{array}{rl}p(z,Tz)& \le p(z,Sz)+p(Sz,Tz)-p(Sz,Sz)\\ =p(z,Sz)+p(Sz,Tz)-p(z,Sz)\\ =p(Sz,Tz).\end{array}$$

(3.12)

Similarly, by (p₄) and using (3.10), we can obtain

$$p(z,Sz)\le p(Sz,Tz).$$

(3.13)

Suppose that $p(Tz,Sz)>0$. Then, since $z⪯z$, by inequality (3.1) and using (3.12), (3.13), we have

$$\begin{array}{rl}p(Tz,Sz)& \le \mathbf{M}(z,z)\\ =(B+D)p(z,Tz)+(C+E)p(z,Sz)\\ \le (B+C+D+E)p(Sz,Tz)\\ <p(Sz,Tz)\end{array}$$

(since $B+C+D+E\le A+B+C+D+2E<1$) which is a contradiction. Thus, $p(Sz,Tz)=0$. By (p₁), we conclude that $Sz=Tz$, that is, z is a coincidence point of T and S. From (3.12), (3.13) and (p₁), we conclude that $Tz=z$ and $Sz=z$, that is, z is a common fixed point of T and S.

Suppose that $p(z,Tz)>0$. Then

$$\begin{array}{rl}p(z,Tz)& =p(Tz,Tz)=p(Tz,Sz)\\ \le (B+C+D+E)p(z,Tz)<p(z,Tz),\end{array}$$

a contradiction. Hence, $p(z,Tz)=0$. This implies that

$$p(Sz,z)=0=p(z,Tz).$$

By (p₁), we conclude that $Tz=z$ and $Sz=z$, that is, z is a common fixed point of T and S. Also by (p₂), we can obtain

$$p(Sz,Sz)=0=p(Sz,Tz).$$

Thus, we have proved (3.3).

• (ii) Since $\{x_n\}$ is a nondecreasing sequence, if X is regular, it follows that $x_n⪯z$ for all n. Therefore, for all n, we can use the inequality (3.1) for $x_n$ and z. Since

  

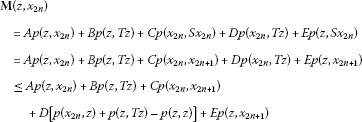
and so ${lim}_{n\to \mathrm{\infty }}\mathbf{M}(z,x_{2n})\le (B+D)p(z,Tz)$. Using (3.9) and (3.1), we have

$$\begin{array}{rl}p(z,Tz)& \le p(z,x_{2n+1})+p(S{x}_{2n},Tz)\\ \le p(z,x_{2n+1})+\mathbf{M}(z,x_{2n}).\end{array}$$

Passing to the limit when $n\to \mathrm{\infty }$, we get that

$$p(z,Tz)\le (B+D)p(Tz,z)<p(Tz,z),$$

which is a contradiction unless $p(z,Tz)=0$. It follows as above that $Tz=z$. Similarly, we can show $p(Sz,z)=0$, that is, $Sz=z$. Hence, z is a common fixed point of T and S. Also, by (p₂), we can obtain $p(Tz,Tz)=0$ and $p(Sz,Sz)=0$.

Now suppose that the set of common fixed points of T and S is well ordered. We claim that a common fixed point of T and S is unique. Assume to the contrary that $Su=Tu=u$ and $Tv=Sv=v$, but $u\ne v$ (and hence $p(u,v)>0$). By supposition, we can replace x by u and y by v in (3.1) to obtain

$$\begin{array}{rl}p(u,v)& =p(Tu,Sv)\le \mathbf{M}(u,v)\\ =Ap(u,v)+Bp(u,Tu)+Cp(v,Sv)+Dp(v,Tu)+Ep(u,Sv)\\ =Ap(u,v)+Bp(u,u)+Cp(v,v)+Dp(v,u)+Ep(u,v)\\ \le (A+B+C+D+E)p(u,v)<p(u,v),\end{array}$$

a contradiction. Hence, $p(u,v)=0$ and $u=v$. Conversely, if T and S have only one common fixed point then the set of common fixed points of T and S, being a singleton, is well ordered. Thus, the proof is complete. □

Standard corollaries of this Hardy-Rogers-type result can be obtained by specifying conditions on the given constants (see [35]). We state just a few of them.

Corollary 3.5 Let $(X,p,⪯)$ be a 0-complete ordered partial metric space. Let $S,T:X\to X$ be two mappings such that S is T-weakly isotone increasing and satisfying either of the following conditions for all comparable $x,y\in X$:

• (1) $p(Tx,Sy)\le Ap(x,y)$, $0\le A<1$;

• (2) $p(Tx,Sy)\le Bp(x,Tx)+Cp(y,Sy)$; $B,C\ge 0$, $B+C<1$;

• (3) $p(Tx,Sy)\le Dp(y,Sx)+Ep(x,Ty)$; $D,E\ge 0$, $D+E<1$.

We suppose also the following:

• (i) S and T are continuous or

• (ii) X is regular.

Then we have conclusions of Theorem 3.3.

We demonstrate Theorem 3.3 with the help of the following example.

Example 3.6 Let $X=[0,+\mathrm{\infty })$ be endowed with the usual partial metric $p:X\times X\to [0,+\mathrm{\infty })$ defined by $p(x,y)=max\{x,y\}$. We give the partial order on X by

$$x⪯y\iff p(x,x)=p(x,y)\iff x=max\{x,y\}\ge y.$$

It is clear that $(X,⪯)$ is totally ordered. The partial metric space $(X,p)$ is 0-complete. Define mappings $T,S:X\to X$ as

$$Tx=\frac{x}{2}\text{and}Sx=\frac{x}{3}\text{for }x\ge 0.$$

It is easy to see that S is T-weakly isotone increasing w.r.t. ⪯. Take $A=\frac{1}{2}$, $B=C=0$ and $D=E=\frac{1}{8}$, i.e.,

$$\mathbf{M}(x,y)=\frac{1}{2}p(x,y)+\frac{1}{8}p(y,Tx)+\frac{1}{8}p(x,Sy)$$

(the conditions on coefficients are fulfilled). Consider the following cases:

1^∘ $x⪯y$, i.e., $y\le x$. Then

$$p(Tx,Sy)=max\{\frac{x}{2},\frac{y}{3}\}=\frac{x}{2},$$

and

$$\mathbf{M}(x,y)=\frac{1}{2}x+\frac{1}{8}max\{y,\frac{x}{2}\}+\frac{1}{8}x\ge \frac{5}{8}x+\frac{1}{16}x=\frac{11}{16}x$$

(cases $y<\frac{x}{2}$ and $\frac{x}{2}\le y\le x$ have to be considered). Hence, $p(Tx,Sy)=\frac{1}{2}x\le \frac{11}{16}x=\mathbf{M}(x,y)$ is fulfilled.

2^∘ $\frac{2}{3}y\le x<y$. Then again $p(Tx,Sy)=\frac{x}{2}$ and

$$\mathbf{M}(x,y)=\frac{1}{2}y+\frac{1}{8}y+\frac{1}{8}max\{x,\frac{y}{3}\}=\frac{5}{8}y+\frac{1}{8}x.$$

Hence, $p(Tx,Sy)=\frac{x}{2}\le \frac{3}{4}x\le \frac{5}{8}y+\frac{1}{8}x=\mathbf{M}(x,y)$.

3^∘ $x<\frac{2}{3}y$. Then

$$\mathbf{M}(x,y)=\frac{5}{8}y+\frac{1}{8}max\{x,\frac{y}{3}\}\ge \frac{16}{24}y>\frac{1}{3}y=p(Tx,Sy).$$

All the conditions of Theorem 3.3 are fulfilled. T and S have a unique common fixed point $z=0$.

Note that in Theorem 3.3 there is no condition of the type ‘there exists an $x_0\in X$ with $x_0⪯T{x}_0$’ of Theorem 2.1. And conditions on coefficients are not the same. Hence, Theorem 2.1 is not a direct consequence of Theorem 3.3. Instead, putting $S=T$ in Theorem 3.3, we obtain the following

Corollary 3.7 Let $(X,p,⪯)$ be a 0-complete ordered partial metric space. Let $T:X\to X$ be a mapping satisfying $Tx\le T^{2}x$ for each $x\in X$ and

$$p(Tx,Ty)\le Ap(x,y)+Bp(x,Tx)+Cp(y,Ty)+Dp(y,Tx)+Ep(x,Ty)$$

for all comparable $x,y\in X$, where $A,B,C,D,E\ge 0$, $A+B+C+D+2E<1$ and $A+B+C+2D+E<1$. We suppose the following:

• (i) T is continuous or

• (ii) X is regular.

Then T has a fixed point z and $p(z,z)=p(Tz,Tz)=p(z,Tz)=0$. Moreover, the set of fixed points of T is well ordered if and only if it is a singleton.