- Research
- Open access
- Published:
Fixed points for G-contractions on uniform spaces endowed with a graph
Fixed Point Theory and Applications volume 2012, Article number: 182 (2012)
Abstract
In this paper, we generalize some main results of (Jachymski in Proc. Am. Math. Soc. 136:1359-1373, 2008) from metric to uniform spaces endowed with an ℰ-distance and a graph using a new type of contractions by employing a class of nondecreasing functions.
MSC:47H10, 05C40.
1 Introduction and preliminaries
In 2004, the concepts of ℰ-distance and S-completeness were introduced for uniform spaces in [1]. Recently in 2008, Jachymski [2] proved some fixed point results in metric spaces endowed with a graph and generalized simultaneously the Banach contraction principle from metric and partially ordered metric spaces. In 2010, Bojor [3] introduced -contractions and generalized Jachymski’s results. Finally, Nicolae et al. [4] presented some fixed point results for a new type of contractions using orbits and also for G-asymptotic contractions in metric spaces endowed with a graph.
The aim of this paper is to generalize Theorems 3.1, 3.2, 3.3 and 3.4 and Proposition 3.1 of Jachymski [2] from metric to uniform spaces endowed with a graph and to present a new type of contractive mappings. The reader interested in (ordered) uniform fixed point theorems may consult the references [5–7].
Following Willard [8], a uniformity on a nonempty set X is a nonempty family of subsets of satisfying the following conditions:
(U1) Each contains the diagonal ;
(U2) is closed under finite intersections;
(U3) For each , the set is a member of ;
(U4) For each , there exists a member V of such that whenever for all ;
(U5) contains the supersets of its elements.
Given a uniformity on a nonempty set X, the pair , simply denoted by X, is called a uniform space.
A uniformity on a nonempty set X is separating if the intersection of all members of is equal to . In this case, X is called a separated uniform space.
We are now ready to recall the concepts of ℰ-distance and p-completeness introduced by Aamri and El Moutawakil [1].
Definition 1 ([1])
Let X be a uniform space. A function is said to be an ℰ-distance on X if
-
(i)
for each , there exists a positive number δ such that whenever and for all ;
-
(ii)
p satisfies the triangular inequality, i.e.,
A sequence in a uniform space X equipped with an ℰ-distance p is said to be p-convergent to a point , denoted by , if as , and p-Cauchy if as . The uniform space X is said to be p-complete if each p-Cauchy sequence in X is p-convergent to some point of X.
The next lemma shows that in a separated uniform space every sequence is p-convergent to at most one point. The proof is straightforward, and hence it is omitted here.
Lemma 1 ([1])
Let be a sequence in a separated uniform space X equipped with an ℰ-distance p, and . If and , then . In particular, if for some , then .
Example 1 Suppose that the set is endowed with the trivial uniformity, that is, . Putting for all , it is seen that p is an ℰ-distance on X and each sequence (and even each net) in X is p-convergent only to zero, but clearly, this space is not separated. Therefore, the converse of Lemma 1 is not true in general.
We next review some basic notions of graph theory in relation to uniform spaces that we need in the sequel. For more details on the theory of graphs, see, e.g., [9].
Let X be a uniform space equipped with an ℰ-distance p and consider a directed graph G with and , that is, contains all loops. Suppose further that G has no parallel edges. The graph G may be considered a weighted graph by assigning the nonnegative number to each edge in .
We denote by the conversion of the graph G, that is, and
The undirected graph obtained from G by ignoring the directions of the edges of G is denoted by . Indeed, can be treated as a directed graph for which the set is a symmetric subset of , namely .
If x and y are two vertices in a graph G, then a path in G from x to y is a finite sequence consisting of vertices of G such that , , and for , where  . A graph G is said to be connected if there exists a path in G between each two vertices of G, and weakly connected if the graph is connected.
. A graph G is said to be connected if there exists a path in G between each two vertices of G, and weakly connected if the graph is connected.
By a subgraph of G, we mean a graph H satisfying and such that contains the vertices of all edges of .
If and is symmetric, then the subgraph consisting of all edges and vertices that are contained in some path in G that starts at x is called the component of G containing x. Thus, , where is the equivalence class of x in the equivalence relation ∼ defined by
It is clear that the graph is connected for all .
2 Main results
Throughout this section, we assume that X is a uniform space that is endowed with an ℰ-distance p and a directed graph G with and unless stated otherwise.
We denote by the set of all fixed points for a self-map f on X, and further by Φ the class of all nondecreasing functions φ from into .
Following Jachymski [2], we introduce -contractions on a uniform space endowed with an ℰ-distance and a graph.
Definition 2 Let f be a self-map on X and φ be a function in Φ. Then f is called a -contraction if
(C1) the edges of G are preserved by f, i.e., implies for all ;
(C2) the p-weights of the edges of G are φ-decreased by f in the sense that
for all with .
If p is a metric on X, then we call f a -contraction, and we call f a -contraction if (1) holds for all .
We now give some examples of -contractions.
Example 2 If for some , since contains all loops, it follows that the constant mapping is a -contraction for any . In particular, for all if and only if each constant mapping on X is a -contraction for some .
Example 3 Each -contraction is a -contraction, where is the complete graph with , that is, .
Example 4 Suppose that ⪯ is a partial order on X and consider the poset graph , that is, and
Then Condition (C1) means that f is nondecreasing with respect to ⪯, and Condition (C2) means that f is an order -contraction, i.e., (1) holds for all with .
In the next example, we construct a self-map f that fails to be a -contraction for any , whereas f is a -contraction for some ℰ-distance p and some .
Example 5 Let be endowed with the usual uniformity (see [[8], p.239]) and the graph . Let and consider a self-map f on X defined by the rule
Then f is not a -contraction for any . Because, setting and , we have
Now, put for all and define by
Clearly, and an easy argument shows that Conditions (C1) and (C2) are satisfied. Thus, f is a -contraction.
Example 6 Consider the mapping f on  defined by for all
defined by for all  . Let G be an arbitrary weakly connected graph with
. Let G be an arbitrary weakly connected graph with  and
and  and φ be any function in Φ. Since G is weakly connected, there exists two distinct points
and φ be any function in Φ. Since G is weakly connected, there exists two distinct points  such that . Then
such that . Then
Therefore, f is not a -contraction for any weakly connected graph G (with  and
and  ) and any function . Now let
) and any function . Now let  be equipped with the trivial uniformity . Then
be equipped with the trivial uniformity . Then  defined by for all
defined by for all  is an E-distance on
is an E-distance on  , and the mapping f is a -contraction for any function .
, and the mapping f is a -contraction for any function .
Example 7 Let be endowed with the usual uniformity and define by
Then f is not a -contraction for any since
On the other hand, defining ‘⪯’ by
the same argument shows that f fails to be a -contraction for any .
Now, set and
Then f is a -contraction if we define by the rule .
Remark 1 It is worth mentioning that Conditions (C1) and (C2) are independent of each other. For instance, the identity mapping on  preserves the edges of , but there is no for which the contractive condition (1) holds. Conversely, setting for all
preserves the edges of , but there is no for which the contractive condition (1) holds. Conversely, setting for all  , it is seen that f is an order -contraction for the constant function but f fails to be nondecreasing.
, it is seen that f is an order -contraction for the constant function but f fails to be nondecreasing.
Remark 2 Putting φ the constant function in Definition 2, we get the concept of Banach G-contraction with on a metric space , which was introduced by Jachymski [2].
Definition 3 We say that the sequences and are p-Cauchy equivalent in X if both of them are p-Cauchy and further, as .
Hereafter we assume that φ is an arbitrary fixed function in Φ and is a -contraction unless stated otherwise.
Theorem 1 Consider the following statements:
-
(A)
G is weakly connected.
-
(B)
If f is a -contraction, then and are p-Cauchy equivalent for all .
-
(C)
Each -contraction has at most one fixed point in X.
Then,
-
(i)
(A) implies (B).
-
(ii)
(B) implies (C) provided that X is separated.
-
(iii)
(C) implies (A) provided that for all .
Proof (i) Let be given. Since G is weakly connected, there exists a path in from x to y, i.e., , , and for each i. Because f is a --contraction, we get by induction that
and, furthermore, by the contractive condition (1) and the fact that φ is nondecreasing, we get
for all and all . Hence, by the triangle inequality of p,
where and . Now, the weak connectivity of G gives , and so, setting in (2) yields
for all . Since , it follows that and a standard argument shows that is p-Cauchy. Similarly, is p-Cauchy and hence and are p-Cauchy equivalent.
-
(ii)
Let x and y be two fixed points for f. Since, by the hypothesis, and are p-Cauchy equivalent, it follows that
Because X is separated, Lemma 1 ensures that .
-
(iii)
Suppose on the contrary that G is not weakly connected. Then there exists an such that both sets and are nonempty. Fix any and define by
Clearly, . To get a contradiction, we show that f is a -contraction. If , then , and so either or . Hence, in both cases, , so because . Moreover,
where φ is any arbitrary function in Φ. Thus, f is a -contraction. □
Corollary 1 If X is p-complete and G is weakly connected, then there exists an such that for all .
Proof Fix any point . By Theorem 1, is a p-Cauchy sequence in X. Since X is p-complete, there exists an such that . Now, if , then by the p-Cauchy equivalence of and , we have
Therefore, . □
Proposition 1 If for some we have , then is f-invariant and is a -contraction. Moreover, if , then and are p-Cauchy equivalent.
Proof Let . Then there exists a path in from to x, i.e., and for each i. So, for each i, that is, is a path in from to fx, and since , there is another path in from to , i.e., , , and for each j. Thus, . Therefore, is f-invariant.
Next, let . This means that there exists a path in from to y such that . Repeating the argument above, we infer that
is a path in from to fy. In particular,
Since , it follows that f is a -contraction.
Moreover, because is weakly connected, Theorem 1 implies that the sequences and are p-Cauchy equivalent for all . □
Following Petruşel and Rus [10], we introduce the concept of a p-Picard operator.
Definition 4 A self-map f on X is called a p-Picard operator if f has a unique fixed point in X and for all .
Given a self-map f on X, we denote the set by .
Theorem 2 Let X be p-complete, separated and satisfy the following property:
(∗) For each sequence in X, p-convergent to some , if for all , then there exists a subsequence of such that for all .
Then
-
(i)
is a p-Picard operator for each .
-
(ii)
If and G is weakly connected, f is a p-Picard operator.
-
(iii)
.
-
(iv)
if and only if .
-
(v)
f has a unique fixed point if and only if there exists an such that .
Proof (i) Let . Then , and so by Proposition 1 and Corollary 1, there exists an such that for all . Since , it follows from Condition (C1) that
By the property (∗), there exists a subsequence of such that for all .
Now, by (3), we see that is a path in from x to , that is, . Moreover, because f is a -contraction, it follows that
Letting , it is concluded that , and since , Lemma 1 yields . If is a fixed point for f, since , it follows that . Furthermore, since, by Proposition 1, is p-Cauchy equivalent to itself, it follows that . Now, again by Lemma 1, . Thus, is a p-Picard operator.
-
(ii)
If G is weakly connected, then , where , and so, by (i), f is a p-Picard operator.
-
(iii)
Set and define a mapping by
We are going to show that θ is a bijection. Since , it follows that , and hence θ is well-defined. On the other hand, if , then by Theorem 1, there exists an such that
which implies that
Thus, θ is surjective.
Now, if are such that , then . So, by Proposition 1 and Theorem 1,
Therefore, . Consequently, θ is injective.
(iv), (v) They are immediate consequences of (iii). □
Remark 3 In [11], Gwóźdź-Łukawska and Jachymski proved some fixed point results for iterated function systems of G-contractions, and in [[11], Example 2], they explicitly claimed that none of [[11], Theorems 4-7] can be generalized to the family of all edge-preserving self-maps satisfying the contractive condition
where  is nondecreasing and satisfies for all . More precisely, their example contains a fixed point free -contraction (in the sense of [[3], Definition 2.1]) and hence it contradicts [[3], Theorem 2.3, (2)], which implies the existence of a fixed point for such a mapping. It might be interesting for the reader why the mapping f in this example does not satisfy (1), which is the main condition of Theorem 2 of this paper and so the example is not in contrary with that theorem. We give the following two reasons:
is nondecreasing and satisfies for all . More precisely, their example contains a fixed point free -contraction (in the sense of [[3], Definition 2.1]) and hence it contradicts [[3], Theorem 2.3, (2)], which implies the existence of a fixed point for such a mapping. It might be interesting for the reader why the mapping f in this example does not satisfy (1), which is the main condition of Theorem 2 of this paper and so the example is not in contrary with that theorem. We give the following two reasons:
-
(1)
Let f and φ be as in [[11], Example 2]. Since for each , we have
it shows that f is not a -contraction, i.e., it does not satisfy
In particular, f is not a -contraction;
-
(2)
In essence, the mapping f in [[11], Example 2] fails to be a -contraction for any . Otherwise, if f is a -contraction for some , then from
we have
By the monotonicity of φ, it follows that the sequence is nonincreasing and bounded from below. Therefore,
which is a contradiction.
Example 8 Let be endowed with the Euclidean metric and define a graph by and
Clearly, X is complete and is weakly connected. Consider f defined by if , and if . Then f is edge-preserving but given , it is seen that
So, f is not a Banach -contraction in the sense of [[2], Definition 2.1] and we cannot use [[2], Theorem 3.2].
Now, uniformize X with the usual uniformity and consider an ℰ-distance p on X by . Then X is separated, p-complete and satisfies the property (∗). Moreover, . Therefore, considering φ as in Example 5, it is seen that f is a -contraction, and so by Theorem 2, f is a p-Picard operator with the unique fixed point zero.
Our next result is a generalization of [[2], Corollary 3.2].
Corollary 2 Let X be p-complete, separated and satisfy the property (∗), and for all . Then the following statements are equivalent:
-
(i)
G is weakly connected;
-
(ii)
If f is a -contraction such that for some , then f is a p-Picard operator;
-
(iii)
Each -contraction has at most one fixed point in X.
Proof (i) ⇒ (ii): It follows immediately from Theorem 2.
-
(ii)
⇒ (iii): Let f be a -contraction. If , then there is nothing to prove. Otherwise, by Theorem 2, . Thus, by the hypothesis, f is a p-Picard operator and so it has a unique fixed point.
-
(iii)
⇒ (i): It follows from Theorem 1. □
Following the idea of Jachymski [2], we define two different types of p-continuity of self-maps on X and then we discuss them.
Definition 5 Let f be a self-map on X. We say that
-
(i)
f is orbitally p-continuous if for each and each sequence of positive integers, implies .
-
(ii)
f is graph orbitally p-continuous if for each and each sequence of positive integers with for such that , one has .
It is clear that p-continuity (see [[1], Definition 2.3]) implies orbital p-continuity, and orbital p-continuity implies graph orbital p-continuity. But the converse of these relations is not true in general as the next example shows.
Example 9 Let be endowed with the uniformity induced by the usual metric.
-
(i)
Consider an ℰ-distance p on X defined by and a self-map f defined by the rule if and . Then f is orbitally p-continuous since implies that . But f fails to be p-continuous because , whereas
 .
. -
(ii)
Next, consider the ℰ-distance on X and the graph G with . Then the self-map f on X defined by the rule if and is graph orbitally p-continuous since for all n implies that is a constant sequence. But setting and , it is seen that , whereas
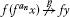 .
.
Theorem 3 Let X be p-complete and separated, and be an orbitally p-continuous -contraction. Then
-
(i)
for each with , there exists an such that for all .
-
(ii)
if and only if there exists an such that .
-
(iii)
If G is weakly connected, f is a p-Picard operator.
Proof (i) Let be such that , and let . Since X is p-complete, by Proposition 1, and are p-convergent to a same point . Since f is orbitally p-continuous, it follows that
On the other hand, , and so by Lemma 1, we have , that is, . Moreover, if z is any other point in , then it is clear that .
-
(ii)
If there exists an such that , then, by (i), we have . The converse is trivial.
-
(iii)
Since G is weakly connected, it follows that for all . So, by (i), there exists an such that for all . Now, similar to the proof of Theorem 2, one can show that is the only fixed point for f, and hence f is a p-Picard operator. □
A generalization of [[2], Corollary 3.3] is given in the next result.
Corollary 3 Let X be p-complete and separated, and for all . Then the following statements are equivalent:
-
(i)
G is weakly connected;
-
(ii)
Each orbitally p-continuous -contraction is a p-Picard operator;
-
(iii)
Each orbitally p-continuous -contraction has at most one fixed point in X.
In particular, if is disconnected, then there exists an orbitally p-continuous --contraction that has at least two fixed points in X.
Proof (i) ⇒ (ii): It follows from Theorem 3.
-
(ii)
⇒ (iii): It is trivial.
-
(iii)
⇒ (i): According to the proof of Theorem 1, it suffices to show that the self-map f is orbitally p-continuous. To this end, let and be a sequence of positive integers such that . Then is either the constant sequence or the constant sequence . If the former holds, then . Since , it follows by Lemma 1 that . Therefore,
Otherwise, if the latter holds, a similar argument shows that f is orbitally p-continuous. □
Theorem 4 Let X be p-complete and separated, and be a graph orbitally p-continuous -contraction. Then
-
(i)
for each , there exists an such that for all .
-
(ii)
if and only if .
-
(iii)
If and G is weakly connected, f is a p-Picard operator.
Proof (i) Let be such that , and let . Since X is p-complete, by Proposition 1, and are p-convergent to a same point . Moreover, for all . Since f is graph orbitally p-continuous, it follows that . On the other hand, because
Lemma 1 ensures that , that is, .
-
(ii)
If , then, by (i), . Conversely, suppose that . Since , it follows that .
-
(iii)
If , since G is weakly connected, we have . Hence, by (i), there exists an such that for all . Now, similar to the proof of Theorem 2, it is seen that is the only fixed point for f. □
Remark 4 In all theorems and corollaries above, setting (), we get the usual (ordered) version of fixed point theorems in (partially ordered) uniform spaces.
References
Aamri M, El Moutawakil D: Common fixed point theorems for E -contractive or E -expansive maps in uniform spaces. Acta Math. Acad. Paedagog. Nyházi. (N.S.) 2004, 20: 83–91.
Jachymski J: The contraction principle for mappings on a metric space with graph. Proc. Am. Math. Soc. 2008, 136: 1359–1373.
Bojor F: Fixed point of φ -contraction in metric spaces endowed with a graph. An. Univ. Craiova, Ser. Mat. Inform. 2010, 37: 85–92.
Nicolae A, O’Regan D, Petruşel A: Fixed point theorems for singlevalued and multivalued generalized contractions in metric spaces endowed with a graph. Georgian Math. J. 2011, 18: 307–327.
Altun I, Imdad M: Some fixed point theorems on ordered uniform spaces. Filomat 2009, 23: 15–22. 10.2298/FIL0903015A
Tarafdar E: An approach to fixed-point theorems on uniform spaces. Trans. Am. Math. Soc. 1974, 191: 209–225.
Turkoglu D, Binbasioglu D: Some fixed-point theorems for multivalued monotone mappings in ordered uniform spaces. Fixed Point Theory Appl. 2001., 2011: Article ID 186237
Willard S: General Topology. Addison-Wesley, London; 1970.
Bondy JA, Murthy USR: Graph Theory. Springer, New York; 2008.
Petruşel A, Rus IA: Fixed point theorems in ordered L -spaces. Proc. Am. Math. Soc. 2006, 134: 411–418.
Gwóźdź-Łukawska G, Jachymski J: IFS on a metric space with a graph structure and extensions of the Kelisky-Rivlin theorem. J. Math. Anal. Appl. 2009, 356: 453–463. 10.1016/j.jmaa.2009.03.023
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Aghanians, A., Fallahi, K. & Nourouzi, K. Fixed points for G-contractions on uniform spaces endowed with a graph. Fixed Point Theory Appl 2012, 182 (2012). https://doi.org/10.1186/1687-1812-2012-182
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2012-182
 .
. .
.